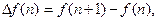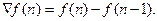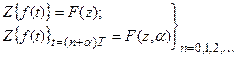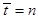Решетчатые функции разности и разностные уравнения

Решетчатые функции разности и разностные уравнения

1. Решетчатые функции и разностные уравнения (определения, понятие конечных разностей).

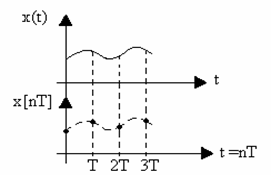
Решетчатая функция времени x [ nT ], или в сокращенной записи x [ n ] — это математическая функция, значения которой определены в дискретные равноотстоящие друг от друга моменты времени t = nT , где n — целое положительное число 0, 1, 2 . а Т — период дискретности. То есть решетчатая функция представляет собой числовую последовательность:

x [0], x [1T], x [2T], x [3T], . , x [ kT ], . .

Если период дискретности T задан, то решетчатая функция однозначно формируется из исходной непрерывной. Операция замены непрерывной функции решетчатой

(1.2)

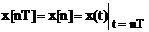
показана на рис. 1.3.

Обратная задача — формирование непрерывной функции из решетчатой — не может быть решена однозначно без дополнительных сведений о поведении функции в интервале между точками t = nT , так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций.

Возникает вопрос, при каких условиях возможно точное восстановление квантованной функции. Ответ на него дает теорема Котельникова-Шеннона [5]: непрерывный сигнал x ( t ), частотный спектр которого ограничен полосой 0 f f _п , полностью определяется последовательностью своих дискретных значений, если период повторения Т этих значений удовлетворяет условию

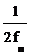
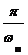
Т или Т , (1.3)

где f _п [ Гц], w _п [с -1 ] — частота пропускания.

Рис. 1.3.Временные диаграммы изменения непрерывной функции x ( t )

и решетчатой функции x [ nT ]

Разностные уравнения (уравнения в конечных разностях) связывают между собой решетчатые функции и их конечные разности. При использовании прямых разностей неоднородные линейные разностные уравнения m-го порядка имеют вид [2]

b₀ D m y[n, s ] + b₁ D m — 1 y[n, s ] + . + b_{m — 1} D y[n, s ] + b_my [n, s ] = f[n, s ], (1.16)

где f [ n , s ] — заданная, а y [ n , s ] — искомая решетчатые функции. При f [ n , s ] º 0 уравнение (1.16) становится однородным разностным уравнением, решением которого будет y [ n , s ].

При использовании (1.9) разностное уравнение (1.16) можно записать в другом виде:

a₀y[ n+m , s ] + a₁y[ n+m — 1, s ] + . + a _m y [n, s ] = f[n, s ]. (1.17)

Коэффициенты этого уравнения определяются

, (1.18)

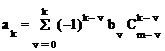
где биноминальные коэффициенты (число сочетаний)

. (1.19)

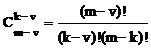
При использовании обратных разностей неоднородные линейные разностные уравнения m-го порядка будут

b₀ Ñ m y[n, s ] + b₁ Ñ m — 1 y[n, s ] + . + b_{m — 1} Ñ y[n, s ] + b_my [n, s ] = f[n, s ]. (1.20)

С учетом (1.10) последнее выражение приобретает вид

a₀y[ n , s ] + a₁y[ n — 1, s ] + . + a _m y [ n — m , s ] = f [ n , s ]. (1.21)

Коэффициенты этого уравнения определяются

, (1.22)

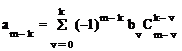
где биноминальные коэффициенты (число сочетаний)

. (1.23)

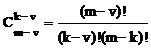
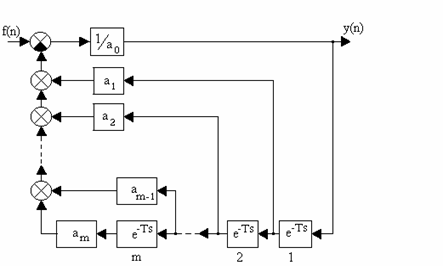
Разностные уравнения можно рассматривать как рекуррентные соотношения, позволяющие вычислять значения y [ n+m , s ] при n = 0, 1, 2, . для уравнения (1.17) и заданных начальных значений y [0, s ], y [1, s ], . y [m-1, s ] или значения y [ n , s ] при n = 0, 1, 2, . для уравнения (1.21) и заданных начальных значений y [ n-m , s ], y [n-m+1, s ], . y [n-1, s ].

Решение уравнения (1.21) при s = 0 представляет собой рекуррентную формулу:

, для n=0, 1, 2, . (1.24)

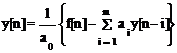
при нулевых начальных условиях y [ n ] º 0 при n

Рис. 1.4.Структурная схема решения разностного уравнения

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

y [ n , s ] = 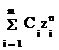, (1.25)

где z _i — корни характеристического уравнения

C _i — постоянные коэффициенты.

Для получения возможности исследования решений разностных уравнений в общем виде широко используются дискретное преобразование Лапласа, z-преобразование, w-преобразование, а также частотные методы.

Решетчатые функции, разности и суммы решетчатых функций

Сигналы в импульсных и цифровых системах подвергаются квантованию, поэтому воздействия в таких системах целесообразно рассматривать как дискретные или решетчатые функции.

Решетчатой функцией называется такая функция, значения которой определяются только при дискретных равноотстоящих друг от друга значениях независимой переменной; между этими значениями независимой переменной решетчатая функция равна нулю. Таким образом, решетчатые функции содержат информацию о соответствующей непрерывной функции лишь в дискретные моменты времени, определяемые периодом квантования, а при других значениях аргумента равны нулю.

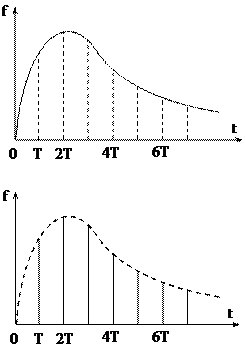Рис. 18.1. Решетчатая функция

На рис.18.1 показаны непрерывная функция f(t) и соответствующая ей решетчатая функция с периодом квантования Т, которая обозначается символом f(nT). Решетчатая функция f(nT) совпадает с исходной непрерывной функцией f(t) только в момент времени nT, где n – любое целое число. Ординаты решетчатой функции при значениях аргумента nt (n=0,1,2,…) называют дискретами. Например, непрерывной функции f(t)=sinwt соответствует решетчатая функция f(nT)=sinwnT, где Т – период прерывания, а n=0,1,2,¼

Каждой непрерывной функции f(t) можно привести в соответствие множество решетчатых функций, отличающихся периодом повторения или смешанных относительно друг друга.

Смешанные решетчатые функции имеют одинаковый период повторения Т, но сдвинуты относительно друг друга на интервал Dt, причем ôDtô£Т. Смещенная решетчатая функция записывается так:

,

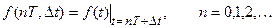
а Dt может рассматриваться как некоторый параметр.

Очевидно, при Dt>0 смещенная решетчатая функция 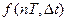сдвигается вправо относительно решетчатой функции f(nT) (здесь Dt=0), а при Dt

Первая прямая разность определяется так:

а первая обратная разность

Эти разности показаны на рис.18.2.

Различие между прямой и обратной разностями решетчатой функции для момента времени t=nT заключается в том, что прямая разность находится по будущему значению решетчатой функции при t=T(n+1), а обратная разность – по прошлому значению решетчатой функции при t=T(n-1).

Вторые разности решетчатой функции определяются так:

,

.

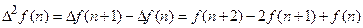
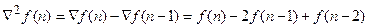
В общем случае имеем:

; (18.1)

, (18.2)

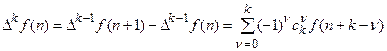
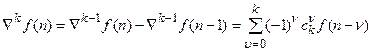
где 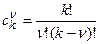— биномиальные коэффициенты (число сочетаний).

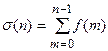
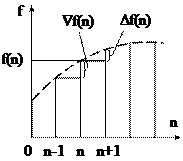Сумма решетчатой функции является аналогом интеграла непрерывной функции в пределах от 0 до t.

Рис. 18.3. Прямые разности решетчатой функции

2. Понятие о разностных уравнениях

Разностные уравнения являются аналогом дифференциальных уравнений и служат для описания динамических процессов в дискретных системах.

Неоднородное разностное уравнение (уравнение в конечных разностях) через прямые разности может быть записано так:

, (18.3)

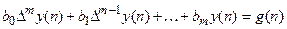
где g(n) – заданная, а y(n) – определяемая решетчатые функции.

При 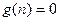уравнение (18.3) становится однородным.

Учитывая (18.1), уравнение (18.3) можно представить так:

, (18.4)

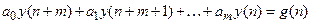
где связь между коэффициентами уравнений (18.3) и (18.4) имеет вид

.

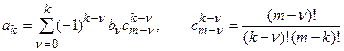
Неоднородное разностное уравнение через обратные разности может быть записано следующим образом:

, (18.5)

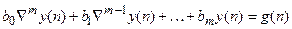
Учитывая (18.2), уравнение (18.5) принимает вид

, (18.6)

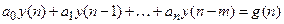
где связь между коэффициентами уравнений (18.5) и (18.6) выражается так:

.

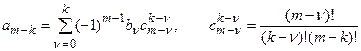
При решении разностных уравнений (18.4) их можно рассматривать как рекуррентные соотношения для вычисления значения y(n+m) при n=0,1,2,¼ , если заданы начальные значения y(0), y(1), ¼, y(m-1). Аналогично по уравнению (18.6) можно определить значения y(n) при n=0,1,2,¼ для заданных начальных значений y(n-m), y(n-m-1), y(n-1). Схема этих вычислений весьма проста и для переменных во времени коэффициентов b_i,a_i (i=0,1,2,¼).

Рассмотрим решение однородного разностного уравнения

. (18.7)

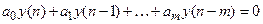
Этому разностному уравнению соответствует характеристическое уравнение

.

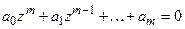
Если через z_i (i=1,2,¼ ,m)обозначить корни этого характеристического уравнения (полагаем, что кратные корни отсутствуют), то общее решение однородного разностного уравнения (18.7) имеет вид

, (18.8)

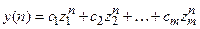
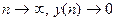
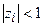
Процесс (18.8) будет затухающим (при ), если будет выполнено условие (i=1,2,¼ ,m).

3. Дискретное преобразование Лапласа. Z-преобразование

Как и для непрерывных функций, при операциях над дискретными функциями используется преобразование Лапласа. Это преобразование, в отличие от обычного, называют дискретным преобразованием Лапласа.

Дискретное преобразование Лапласа для решетчатой функции f(nT) обозначается через F * (p) и определяется таким образом:

, (18.9)

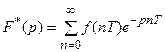
Для смещенной решетчатой функции f(n,T,Dt) получаем

.

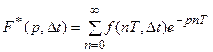
Если решетчатые функции представлены в виде f(n), f(n,a), то для них соответственно имеем:

,

,

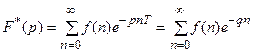
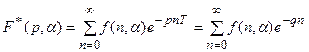
Рассмотрим вспомогательную дискретную функцию f * (nT), которая выражается через исходную непрерывную функцию f(t) следующим образом:

. (18.10)

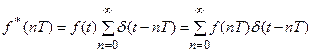
Эта функция представляет собой дискретную последовательность из единичных импульсных функций (d-функций), взятых с коэффициентами, равными значениям исходной непрерывной функции f(t) в соответствующие моменты времени nT (n=0,1,2,¼).

Найдем теперь преобразование Лапласа от этой (16.10) дискретной функции :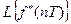

.

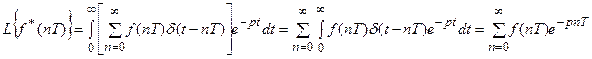
Таким образом, преобразование Лапласа от дискретной импульсной функции (18.10) полностью совпадает с дискретным преобразованием Лапласа от соответствующей решетчатой функции.

Z-преобразование. При исследовании дискретных систем широкое применение получило z-преобразование, которое может быть получено из дискретного преобразования Лапласа (18.2) путем подстановки .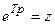

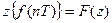
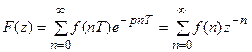
Таким образом, выражение для z-преобразования решетчатой функции f(nT), обозначаемое через , имеет вид

. (18.11)

Соответственно для смещенной решетчатой функции f(n,a) получаем так называемое модифицированное (смешанное) z-преобразование

.

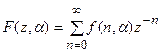
Выражение для z-преобразования могут быть записаны и для непрерывных функций:

Рассмотрим без доказательства основные теоремы z-преобразования.

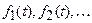
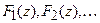
Если функции имеют соответственно z-преобразования , то

где a — постоянная величина.

Теорема сдвига по временной области

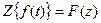
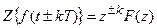
Если , то .

Теорема смещения независимого переменного

(умножение оригинала на экспоненту)

,

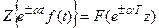
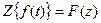
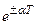
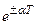
где a — положительное число, а . Следовательно, умножение функции f(t) во временной области на экспоненциальную функцию приводит в z-области к изменению масштаба независимой переменной в раз.

Теорема о конечном значении

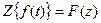
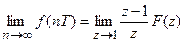
Если не содержит полюсов на окружности единичного радиуса или вне ее, то

.

Эта теорема позволяет определить установившееся значение любой переменной дискретной системы по соответствующему z-преобразованию.

Теорема о начальном значении

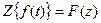
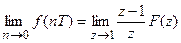
Если , то .

Найдем теперь z-преобразование некоторых характерных функций.

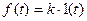
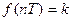
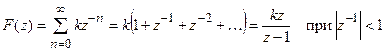
1. Ступенчатая функция . Соответствующая решетчатая функция имеет вид , далее находим

.

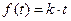
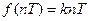
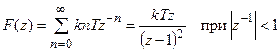
2. Функция с постоянным наклоном . Имеем , находим z-преобразование этой функции

.

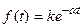
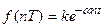
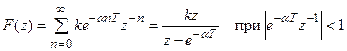
3. Экспоненциальная функция . Имеем , тогда получаем

.

4. Разности решетчатых функций. Для первой прямой разности имеем

.

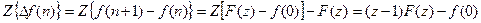
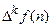
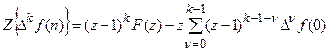
Если рассмотреть , то получим

,

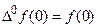
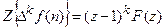
причем . При условии f(0)=f(1)=f(2)=¼=f(k-1)=0 полученное выражение упрощается

.

Для первой обратной разности находим

.

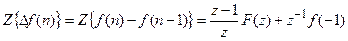
Если для отрицательных аргументов решетчатая функция равна нулю, то получаем

.

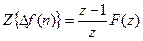
Для k-ой обратной разности при f(n)=0 при n

Дата добавления: 2015-12-11 ; просмотров: 3427 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Математическое описание дискретных систем

Решетчатые функции

Математическое описание импульсных АСУ усложняется из-за дискретного характера сигнала. Квантованный по времени сигнал может быть представлен выборкой ординат непрерывной функции времени (см. рис.1.1). Эти ординаты разделены периодом квантования, а внутри периодов все промежуточные значения равны нулю. Поэтому дискретный сигнал удобно описывать функциями дискретной переменной [6].

Рассмотрим функцию времени , определенную для всех значений t и тождественно равную нулю для (см. рис. 1.1).

Пусть n – натуральное число (n=0,12,3…) и Т – период дискретности. Функцией дискретного аргумента называетсячисловая последовательность f[0], f[T], f[2T],…, f[nT], получающаяся в результате выборки значений функции в точках , n – натуральное число. Для краткости ее называют решетчатой функциейи обозначают f[n].

При заданном интервале дискретности Т по функции решетчатая функция f[n] определяется однозначно. Непрерывная функция – огибающая для своей решетчатой функции f[n]. Но поскольку через дискретные точки решетчатой функции можно провести множество огибающих, то обратного соответсвия между решетчатой функцией и “породившей” ее функцией нет: f[n]® .

Если необходимо определять значения функции между точками квантования, то вводят понятие смещенной решетчатой функции.

Смещенной решетчатой функциейназывается числовая последовательность – f[sT], f[T+sT],…, f[iT+sT],…, f[nT+sT], 0 £ s £ 1, образованная в результате выборки значений функций в точках оси времени, где s – постоянное число, лежащее в интервале 0 £s £ 1. Сокращенно f[n, s].

Поскольку значения решетчатой функции известны только для дискретных значений аргумента, то для изучения поведения таких функций методы дифференциального и интегрального исчисления оказываются непригодными.

Для оценки свойств решетчатой функции используется аппарат конечных разностей и конечных сумм, позволяющий оценивать свойства числовых последовательностей (функций дискретного аргумента).

Для исследования динамики дискретных импульсных АСУ используются разностные уравнения. Их решение, так же как и дифференциальных, представляет известные трудности. В связи с этим, в теории дискретных (импульсных) АСУ широко используются операционные методы.

Разностные уравнения

Если вместо переменной t ввести относительную переменную , то непрерывной функции в относительном масштабе будет соответствовать решетчатая функция . Она совпадает с при

(1.1)

Таким образом, решетчатая функция изменяет свое значение при целочисленных значениях независимого переменного n, а интервал между дискретами равен 1.

Дискретная функция не является однозначной, что видно из рис. 1.15.

Рис. 1.15. Решетчатая функция

Для устранения этой неоднозначности вводят смещенные дискретные функции, позволяющие “просматривать” процессы внутри периодов Т.

Записывают смещенную функцию так

. (1.2)

Однако на основе теоремы Котельникова можно сделать вывод, что если непрерывный сигнал 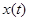не содержит гармоническую составляющую с частотой выше , то при квантовании с периодом дискретная решетчатая функция точно отобразит непрерывную функцию, т.е. потери информации при дискретизации не будет.

Для математического описания динамики дискретных систем применяют разностные уравнения. Они определяют связь между значениями решетчатой функции и, таким образом, форму огибающей данной решетчатой функции. Оценка связи значений решетчатой функции производится с помощью конечных разностей. Они являются аналогами производных в дифференциальных уравнениях.

Переход от дифференциальных уравнений к разностным основан на замене производных разностями соответствующих порядков (табл. 1.1).

Соответствие производных и правых разностей

Порядок производной или разности	Непрерывная функция	Дискретная функция
.	. . .	. . .
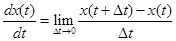m

Первая разность решетчатой функции:

,

и т.д.

То есть, для определения первой разности (рис. 1.16) надо знать два последовательных значения решетчатой функции.

Рис. 1.16. К определению разностей решетчатой функции

Упомянутая выше аналогия между первой разностью и первой производной видна из того, что первая разность, как и первая производная, равна по существу, отношению приращения функции к приращению аргумента

,

,

то ее значение просто равно .

Вторая разность решетчатой функции:

Для нахождения второй разности надо знать три последовательных значения решетчатой функции. Разность m-го порядка определяется выражением

Рассмотрим простой пример дискретной функции и ее первой разности (рис. 1.17). Пусть . Ее первая разность т.е. является единичной ступенчатой дискретной функцией . Вторая и высшие разности этой функции равны нулю.

Рис. 1.17. Пример дискретной функции и ее первой разности

На рис. 1.18 в качестве примера приведена решетчатая функция произвольного вида x[n] (рис. 1.18, а), а также ее первая Dx[n] (рис. 1.18, б) и вторая D 2 x[n] (рис. 1.18, в) разности.

Разностное уравнение k-го порядка соответствует дифференциальному уравнению k-го порядка. Если линейное дифференциальное уравнение записывают в виде

(1.3)

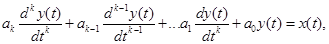
то линейное разностное уравнение с постоянными коэффициентами можно записать так

(1.4)

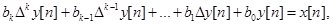
где – известная дискретная функция;

– искомая дискретная функция, получаемая в результате решения разностного уравнения.

Рис. 1.18. Решетчатая функция произвольного вида x[n],

а также ее первая Dx[n] и вторая D 2 x[n] разности

Дифференциальное уравнение можно рассматривать как предельное выражение для разностного уравнения при . Решать разностные уравнения можно различными методами, аналогичными методам решения дифференциальных уравнений.

В теории управления часто применяют операционный метод решения дифференциальных уравнений, который позволяет свести решение к решению алгебраического уравнения.

Для решения разностных уравнений также используют операционный метод, основанный на дискретном преобразовании Лапласа, в частности Z-преобразовании.

1.2.3. Понятие о Z-преобразовании

Метод Z – преобразования нашел широкое применение при исследовании импульсных и цифровых систем управления [6]. Если поведение системы достаточно полно описывается только в дискретные моменты времени, то наиболее удобным математическим аппаратом для анализа и синтеза является аналог преобразования Лапласа – дискретное преобразование Лапласа или так называемое Z – преобразование.

Z – преобразованием решетчатой функции называется функция комплексного аргумента Z, определяемая выражением

. (1.5)

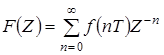
Это выражение может быть получено следующим образом. Если предыстория системы относительно учитывается соответствующими граничными условиями, то допустимо полагать, что непрерывная функция времени при t