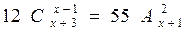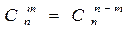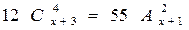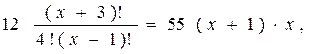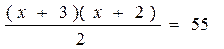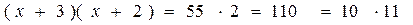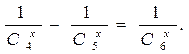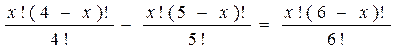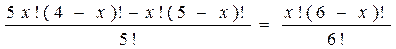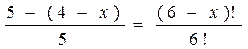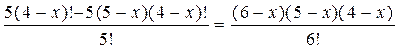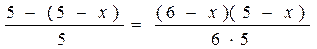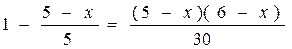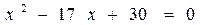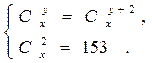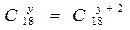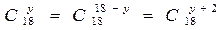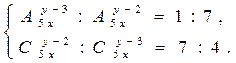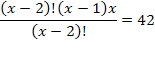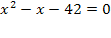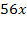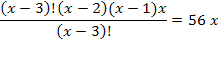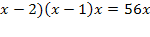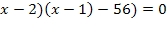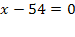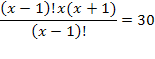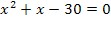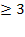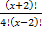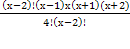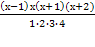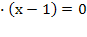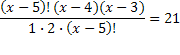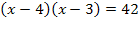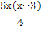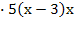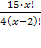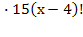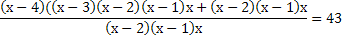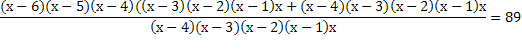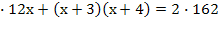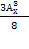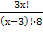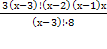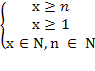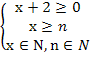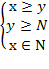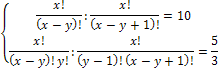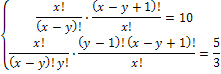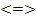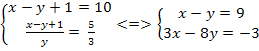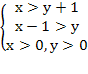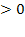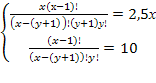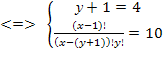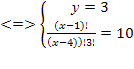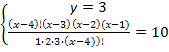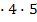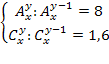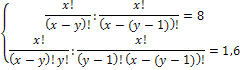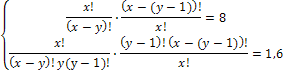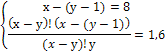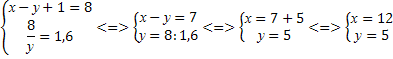Решить комбинаторное уравнение 2x 28

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Решить систему уравнений

Немного теории.

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ \left\< \begin 3x+y=7 \\ -5x+2y=3 \end \right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ \left\< \begin y = 7—3x \\ -5x+2(7-3x)=3 \end \right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 \Rightarrow -5x+14-6x=3 \Rightarrow -11x=-11 \Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 \cdot 1 \Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ \left\< \begin 2x+3y=-5 \\ x-3y=38 \end \right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ \left\< \begin 3x=33 \\ x-3y=38 \end \right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение \( x-3y=38 \) получим уравнение с переменной y: \( 11-3y=38 \). Решим это уравнение:
\( -3y=27 \Rightarrow y=-9 \)

Таким образом мы нашли решение системмы уравнений способом сложения: \( x=11; y=-9 \) или \( (11; -9) \)

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.

Конспект урока на тему «Решение комбинаторных уравнений» (10 класс)

Сочетаниями без повторений занимался еще великий Паскаль. Он предложил специальную таблицу значений сочетаний без повторений.

Значения представлены в табл. которая называется треугольником Паскаля.

Этот треугольник удивительно красив своей математической красотой, и в его числах можно при желании отыскать различные закономерности. Его можно представить несколько иначе – в виде [26]: равнобедренного треугольника (рис. 10).

Рис. 10. Треугольник Паскаля

Здесь каждое число, кроме единиц на боковых сторонах, является суммой двух чисел, стоящих над ним. Поэтому:

(приводим к общему знаменателю)

(выносим n ! за скобку в знаменателе)

Из этого соотношения и вытекает эффективный способ рекуррентного вычисления значений биномиальных коэффициентов.

Докажем соотношение 1)

Это может использоваться при вычислениях, например, вместо можно вычислить .

Докажем соотношение 2)

Имеется формула, называемая биномом Ньютона, которая использует выражения числа сочетаний с повторениями

где а, b – действительные или комплексные числа.

Коэффициенты называются биномиальными.

Докажем формулу бинома Ньютона по индукции. Доказательство по индукции предполагает:

1) базис индукции – доказательство того, что формула верна для конкретного n , например, для n =1. В нашем случае мы убедились, что формула верна для n =2,3,4. Убедимся, что она верна и для n =1.

2) индукционный шаг. Предполагая, что формула верна для некоторого n , убеждаются, что тогда она верна и для n +1.

3) при истинности шагов 1 и 2 заключают, что формула верна для любого n .

Приступим к индукционному шагу.

Возьмем выражение и получим из него выражение для n +1. Очевидно, что это можно сделать путем умножения на a + b :

Преобразуем полученное выражение:

Для выполнения индукционного шага необходимо показать, что это выражение равно выражению:

Рассмотрим подвыражение выражения (1): и заменим i на i -1.

Получим , т.е. одинаковые коэффициенты перед выражениями , для числа сочетаний в первом и втором подвыражении выражения (1).Это позволит вынести за скобку. Но тогда в не учтен n -й член подвыражения (суммирование идет до n ): тогда, учитывая его, получаем:

Нетрудно видеть, что можно заменить на , кроме того, мы уже доказали, что , поэтому: , что, очевидно, равно выражению:

По индукции получаем, что формула бинома Ньютона верна для любого n .

С использованием бинома Ньютона докажем следствие №1 о количестве подмножеств множества из n элементов:

Рассмотрим следствие №2: .

На использовании бинома Ньютона основано понятие производящей функции – функции, позволяющей получать комбинаторные числа без вычисления факториала:

. Здесь – функция, производящая биномиальные коэффициенты.

При n =1 получаем 1+ x , т.е. (коэффициент перед 1), (коэффициент перед x ).

При n =2 получаем (1+ x ) 2 =1+2 x + x 2 , т.е. и т.д.

Решение комбинаторных уравнений

В комбинаторике тоже могут решаться уравнения, особенностью которых является то, что неизвестная принадлежит множеству натуральных чисел. Например, уравнения вида , xN , где N – множество натуральных чисел или вида:

При решении комбинаторных уравнений часто необходимо уметь выполнять действия с факториалами типа:

Например, в задаче о сравнении пар записей в базе данных из n записей:

, – что и требовалось доказать.

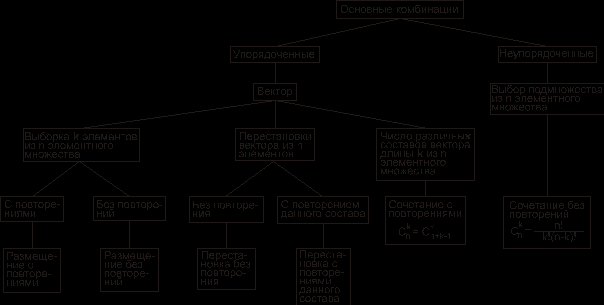
В комбинаторике рассматриваются и другие типовые комбинаторные комбинации, например, разбиения n -элементного множества на k подмножеств, которые называются блоками разбиения. В информатике вычисления на конечных математических структурах часто называют комбинаторными вычислениями, и они требуют комбинаторного анализа для установления свойств и оценки применимости используемых алгоритмов. На рис. 11 приведен один из возможных вариантов классификации основных комбинаций.

Рис. 11. Основные комбинации

Комбинаторные задачи могут быть решены, например, системой компьютерной математики Matematica (3,4) фирмы Wolfram Research , Inc . – пакет расширения «Дискретная математика» ( DiscreteMath ) – комбинаторика и ее функции ( Combinatorica , CombinatorialFunctions ): функции перестановок и сочетаний и др.

Пример 1. Решить уравнение

и представим правую часть в виде

,

откуда следует

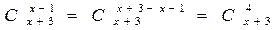
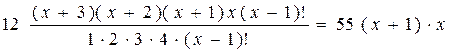
x + 3 = 11 и x = 8.

Пример 2. Решить уравнение

Решение. По условию x – целое число, удовлетворяющее неравенством 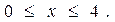Перепишем уравнение в виде

откуда, после упрощений, получаем

> 4

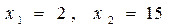
Пример 3. Решить систему уравнений

Решение. Из второго уравнение находим

Решая последнее уравнение, получаем Но так как не пригодно к решению уравнения, значит x = 18.

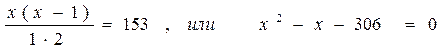
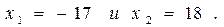
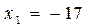
Подставляя x = 18 в первое уравнение системы, найдем

18 – y = y + 2, y = 8.

Итак, x = 18, y = 8.

Пример 4. Решить систему уравнений

Решение. Перепишем систему уравнений в виде

или, после упрощений получим

откуда следует x = 2, y = 6.

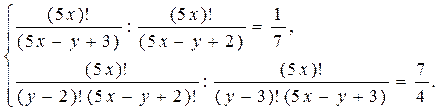
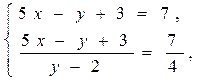
Решите уравнение (22–25) .

1)=42;

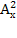
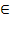
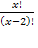
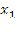
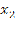
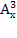
ОДЗ: хN; x > 2

= 42

=-6( исключить – не входит в ОДЗ); =7

=56х;

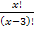
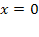
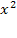
ОДЗ: хN; x > 3

=

(

((

или -3

1 =0(исключить) или х 2 =-6 (исключить); х 3 =9 (входит в ОДЗ).

3)=30;

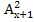
ОДЗ: хN; x+1 > 2; х > 1

=

=-6( исключить – не входит в ОДЗ); =5.

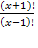
4) 5=;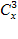

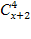
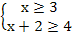
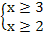
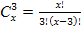
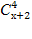
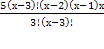
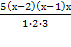
ОДЗ: х

; =

=

=

(20(х-2)-(х+1)(х+2))х

(20х-40-х 2 +2х+х+2)=0 или х=0 или х-1=0

х 2 +3х-20х+42=0 х 1 =0 х 2 =1

х 2 -17х+42=0 корни 0 и 1 не входят в ОДЗ

= 21 ОДЗ: хN; x-3 > 2 ; x > 3

=

— 7х + 12 – 42 = 0

— 7х – 30 = 0

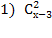
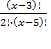
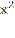
х 1 =10 х 2 = — 3 (не входит в ОДЗ)

2) ; ОДЗ: хN; x > 3

=

=

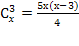
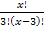
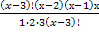
4х(х-2)(х-1) = 6

х(4х 2 – 12х+8-30х+90)=0

х=0 или 4х 2 – 42х + 98 = 0

2х 2 – 21х + 49 = 0

= 15(х-1) ОДЗ: хN; x > 3

= 15(х-1)

= (х-1)х х 1 = 0 или х 2 = 1 — не входят в ОДЗ

= ОДЗ: хN; x > 4

=

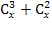
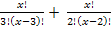
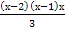
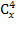
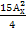
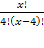
4(х-2)! = 24

х 1 =12; х 2 = — 7(не входит в ОДЗ)

= 43 ОДЗ: хN; x > 5

= 43

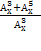
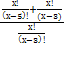
х 1 =10; х 2 = 3 (не входит в ОДЗ)

= 89 ОДЗ: хN; x > 7

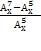
х 2 – 11х – 60 = 0

х 1 =15; х 2 = — 4(не входит в ОДЗ)

+ = 162 ОДЗ: хN; x > 1

= 162

= 162

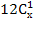
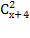
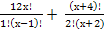
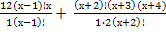
2

24х + х 2 + 7х + 12 – 324 = 0

х 2 + 31х – 312 = 0

х 1 =8; х 2 = — 39(не входит в ОДЗ)

=

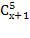
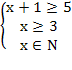
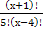
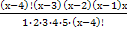
ОДЗ: x > 4

=

=

(х-2)(х-1)х = 0 или (х-3)-45 = 0

х 1 =2; х 2 = 1 х 3 =0 — не входят в ОДЗ х 4 = 48

= 42 ОДЗ: хN; x > 4

= 12

= 12 х 2 – х – 12 = 0 х 1 =4; х 2 = — 3(не входит в ОДЗ) Ответ: 4.

= 90 ОДЗ:

= 90

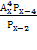
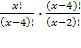
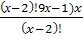
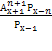
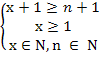
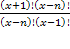
х 1 =10; х 2 = — 9(не входит в ОДЗ)

= 132 ОДЗ:

= 132

= 132

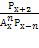
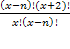
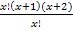
x 2 +3 x +2–132 = 0

х 1 =10; х 2 = — 13(не входит в ОДЗ)

= 110 ОДЗ:

= 110

= 110

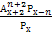
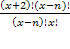
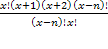
x 2 +3 x +2– 110 = 0

x 2 +3 x – 108 = 0

х 1 =9; х 2 = — 12(не входит в ОДЗ)

ОДЗ:

решаем методом сложения — 5у = -30; у = 6

ОДЗ: ; у

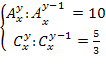
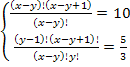
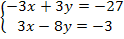
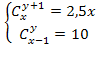
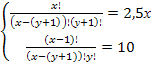
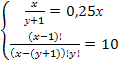
(х-3)(х-2)(х-1) = 3

4)

Сколько двузначных чисел можно составить из цифр 1. 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр?

Из 6 открыток надо выбрать 3. Сколькими способами это можно сделать?

Решить комбинаторное уравнение : C_x ^ 3 + C_x ^ 2 = 15(x — 1)?

Математика | 10 — 11 классы

Решить комбинаторное уравнение : C_x ^ 3 + C_x ^ 2 = 15(x — 1).

Из определений следует, что х&gt ; = 3

раскрываем сокращаем получаем в конце концов кв уравнение относ х

Очень нужна ваша помощь?

Очень нужна ваша помощь!

Надо придумать 2 комбинаторные задачи и решить их !

По логике, Пожалуйста.

Придумайте сами три комбинаторные задачи?

Придумайте сами три комбинаторные задачи!

Придумайте комбинаторную задачу?

Придумайте комбинаторную задачу.

Придумайте комбинаторную задачу про лошадей?

Придумайте комбинаторную задачу про лошадей.

Решите комбинаторные уравнения?

Решите комбинаторные уравнения.

Решите пожалуйста номер 973 за 15 балов?

Решите пожалуйста номер 973 за 15 балов.

Тема : комбинаторные задачи.

Придумайте три комбинаторные задачи?

Придумайте три комбинаторные задачи.

Придумайте сами 3 комбинаторные задачи?

Придумайте сами 3 комбинаторные задачи.

Придумайте сами три комбинаторные задачи?

Придумайте сами три комбинаторные задачи.

Помогите придумать 3 комбинаторные задачи?

Помогите придумать 3 комбинаторные задачи!

Вы открыли страницу вопроса Решить комбинаторное уравнение : C_x ^ 3 + C_x ^ 2 = 15(x — 1)?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

426 : х = 213 х = 426 : 213 х = 2 8 * х = 288 х = 288 : 8 х = 36.

№1. |5| + | — 3| + |8| — | — 15| = 5 + 3 + 8 — 15 = 16 — 15 = 1 №2. | — 13| * | — 5| * |4| = 13 * 5 * 4 = 260 №3. А) |х| = 3 х = — 3 или х = 3 б) |х| = — 1 х — ни чему неравен.

Если у графика «обычного» синуса период — 2π или 360°, то у «нашего — всего 360 : 3 = 120° Амплитуда графика при этом не меняется. Потребуются дополнительные точки. Для синуса : х = 0, у = 0 х = 30, у = 0, 5 х = 60 , у = 0, 87 х = 90, у = 1. Для н..

99 — 88 = 11 Ответ : это число 11. 99 это наибольшее двузначное число.

Наибольшее двузначное число — 99 99 — 88 = 11.

1) 14 * 18 = 252 (км) — высота космического корабля. Рисунки не представлены далее.

Ax + 3x — 2a² — 6a = 0 x(a + 3) — (2a² + 6a) = 0 x(a + 3) — 2(a + 3) = 0 (a + 3)(x — 2) = 0 x — 2 = 0 x = 2 при a∈( — ∞ ; — 3)U( — 3 ; + ∞) x∈( — ∞ ; + ∞) при а = — 3.

1 / 2 — 2 / 7 = 7 / 14 — 4 / 14 = 3 / 14 х — 1 дробь у — 2 дробь х + у = 1 / 2 х — у = 3 / 14 х = у + 3 / 14 у + 3 / 14 + у = 1 / 2 2у = 1 / 2 — 3 / 14 2у = 7 / 14 — 3 / 14 2у = 4 / 14 = 2 / 7 у = 2 / 7 : 2 у = 2 / 7 * 1 / 2 у = 1 / 7 — 2 дробь х = 1..

Ответ 188 : D 44 + 39 = 83 83 — 17 = 66 66 + 99 = 165 165 — 1 = 164 164 + 24 = 188 188 * 2 = 376 376 / 2 = 188.