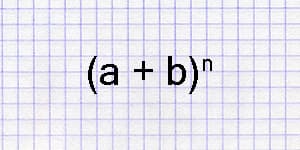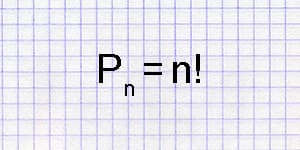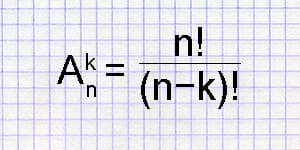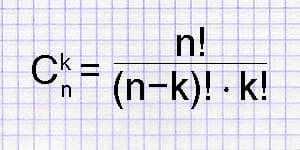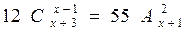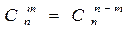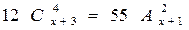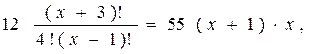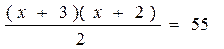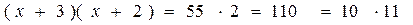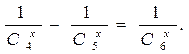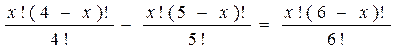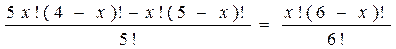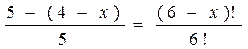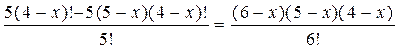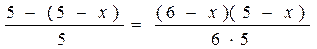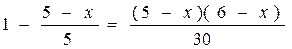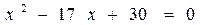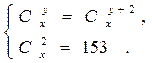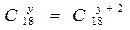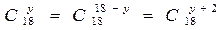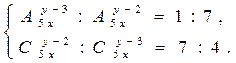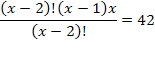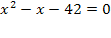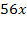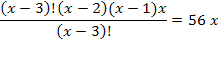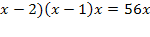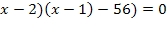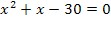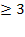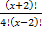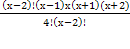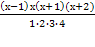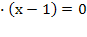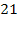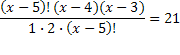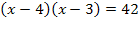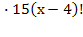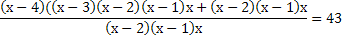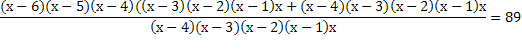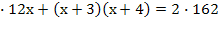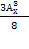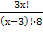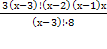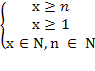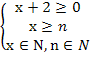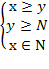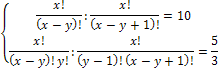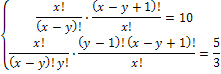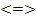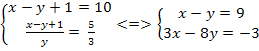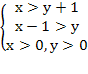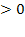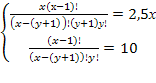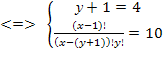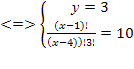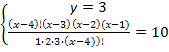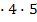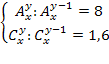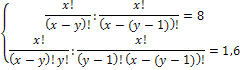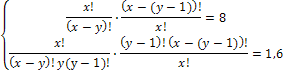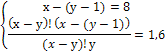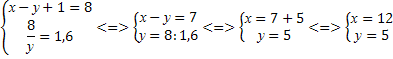Комбинаторика
Комбинаторика онлайн калькуляторы
| Элементы комбинаторики перестановки, размещения, сочетания | Число перестановок находит все варианты перестановки |
| Обратная перестановка онлайн калькулятор | Количество инверсий в перестановке это количество пар элементов |
| Циклическая перестановка перевод цикла в стандарт | Число сочетаний вычисление числа сочетаний из n по k элементов |
| Порядок перестановки стандартной и циклической | Число сочетаний с повторениями онлайн калькулятор для нахождения сочетаний |
| Число размещений нахождение количества размещений | Разложение Бинома Ньютона калькулятор разложения степени |
| Комбинаторные уравнения решение комбинаторных уравнений |
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
Комбинаторика
Комбинаторика – раздел математики, занимающийся изучением количества возможных комбинаций определенного типа, которые возможно сделать из некоторого набора элементов. Эти вычисления необходимы для решения различных задач в теории вероятностей и получения распределений случайных величин.
Правила в комбинаторике
Правило суммы: если есть взаимоисключающие друг друга действия A и B, которые можно выполнить способами m и n соответственно, то выполнить любое из этих действий можно m + n способами.
Правило произведения: если есть последовательность действий k, и первое действие его можно выполнить n1 способом, второе n2 и далее до nk, то все действия этой последовательности можно выполнить n1 · n2 · nk способами.
Элементы комбинаторики
Размещения из n по k – упорядоченное множество, состоящее из k элементов, которые выбраны из n элементов. Для расчета способов размещения следует воспользоваться формулой: P k n = n! / (n — k)!
Перестановки – конечное множество, в котором указан порядок его элементов. Количество перестановок вычисляется по формуле: Pn = n!
Сочетания из n по k – неупорядоченное множество, состоящее из k элементов, которые выбраны из n элементов. Число сочетаний из n элементов по k рассчитывается так: n! / (n — k)! · k!
Калькулятор разложения бинома Ньютона с использованием треугольника Паскаля.
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.
Конспект урока на тему «Решение комбинаторных уравнений» (10 класс)
Сочетаниями без повторений занимался еще великий Паскаль. Он предложил специальную таблицу значений сочетаний без повторений.
Значения представлены в табл. которая называется треугольником Паскаля.
Этот треугольник удивительно красив своей математической красотой, и в его числах можно при желании отыскать различные закономерности. Его можно представить несколько иначе – в виде [26]: равнобедренного треугольника (рис. 10).
Рис. 10. Треугольник Паскаля
Здесь каждое число, кроме единиц на боковых сторонах, является суммой двух чисел, стоящих над ним. Поэтому:
(приводим к общему знаменателю)
(выносим n ! за скобку в знаменателе)
Из этого соотношения и вытекает эффективный способ рекуррентного вычисления значений биномиальных коэффициентов.
Докажем соотношение 1)
Это может использоваться при вычислениях, например, вместо можно вычислить .
Докажем соотношение 2)
Имеется формула, называемая биномом Ньютона, которая использует выражения числа сочетаний с повторениями
где а, b – действительные или комплексные числа.
Коэффициенты называются биномиальными.
Докажем формулу бинома Ньютона по индукции. Доказательство по индукции предполагает:
1) базис индукции – доказательство того, что формула верна для конкретного n , например, для n =1. В нашем случае мы убедились, что формула верна для n =2,3,4. Убедимся, что она верна и для n =1.
2) индукционный шаг. Предполагая, что формула верна для некоторого n , убеждаются, что тогда она верна и для n +1.
3) при истинности шагов 1 и 2 заключают, что формула верна для любого n .
Приступим к индукционному шагу.
Возьмем выражение и получим из него выражение для n +1. Очевидно, что это можно сделать путем умножения на a + b :
Преобразуем полученное выражение:
Для выполнения индукционного шага необходимо показать, что это выражение равно выражению:
Рассмотрим подвыражение выражения (1): и заменим i на i -1.
Получим , т.е. одинаковые коэффициенты перед выражениями , для числа сочетаний в первом и втором подвыражении выражения (1).Это позволит вынести за скобку. Но тогда в не учтен n -й член подвыражения (суммирование идет до n ): тогда, учитывая его, получаем:
Нетрудно видеть, что можно заменить на , кроме того, мы уже доказали, что , поэтому: , что, очевидно, равно выражению:
По индукции получаем, что формула бинома Ньютона верна для любого n .
С использованием бинома Ньютона докажем следствие №1 о количестве подмножеств множества из n элементов:
Рассмотрим следствие №2: .
На использовании бинома Ньютона основано понятие производящей функции – функции, позволяющей получать комбинаторные числа без вычисления факториала:
. Здесь – функция, производящая биномиальные коэффициенты.
При n =1 получаем 1+ x , т.е. (коэффициент перед 1), (коэффициент перед x ).
При n =2 получаем (1+ x ) 2 =1+2 x + x 2 , т.е. и т.д.
Решение комбинаторных уравнений
В комбинаторике тоже могут решаться уравнения, особенностью которых является то, что неизвестная принадлежит множеству натуральных чисел. Например, уравнения вида , xN , где N – множество натуральных чисел или вида:
При решении комбинаторных уравнений часто необходимо уметь выполнять действия с факториалами типа:
Например, в задаче о сравнении пар записей в базе данных из n записей:
, – что и требовалось доказать.
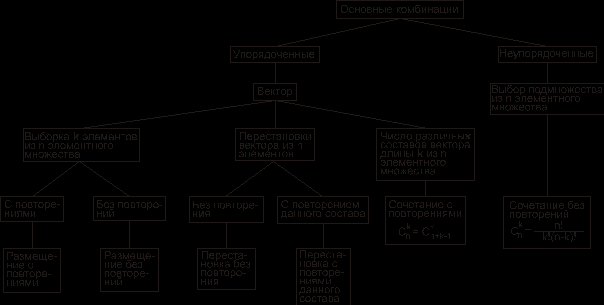
В комбинаторике рассматриваются и другие типовые комбинаторные комбинации, например, разбиения n -элементного множества на k подмножеств, которые называются блоками разбиения. В информатике вычисления на конечных математических структурах часто называют комбинаторными вычислениями, и они требуют комбинаторного анализа для установления свойств и оценки применимости используемых алгоритмов. На рис. 11 приведен один из возможных вариантов классификации основных комбинаций.
Рис. 11. Основные комбинации
Комбинаторные задачи могут быть решены, например, системой компьютерной математики Matematica (3,4) фирмы Wolfram Research , Inc . – пакет расширения «Дискретная математика» ( DiscreteMath ) – комбинаторика и ее функции ( Combinatorica , CombinatorialFunctions ): функции перестановок и сочетаний и др.
Пример 1. Решить уравнение
и представим правую часть в виде
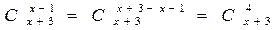
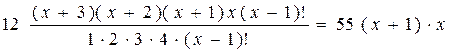
x + 3 = 11 и x = 8.
Пример 2. Решить уравнение
Решение. По условию x – целое число, удовлетворяющее неравенством 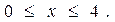
откуда, после упрощений, получаем
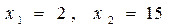
Пример 3. Решить систему уравнений
Решение. Из второго уравнение находим
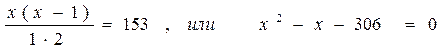
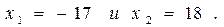
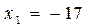
Подставляя x = 18 в первое уравнение системы, найдем
18 – y = y + 2, y = 8.
Итак, x = 18, y = 8.
Пример 4. Решить систему уравнений
Решение. Перепишем систему уравнений в виде
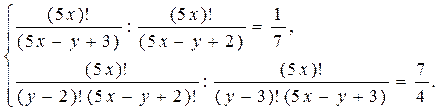
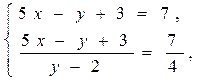
Решите уравнение (22–25) .
1)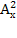
ОДЗ: х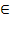
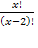
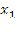
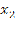
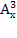
ОДЗ: х
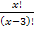
(

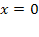
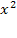

3)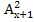
ОДЗ: х
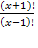


4) 5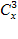
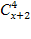
ОДЗ: 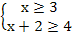
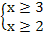
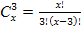
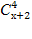
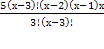
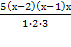
(20(х-2)-(х+1)(х+2))
(20х-40-х 2 +2х+х+2)=0 или х=0 или х-1=0
х 2 +3х-20х+42=0 х 1 =0 х 2 =1
х 2 -17х+42=0 корни 0 и 1 не входят в ОДЗ
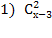

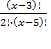
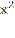

х 1 =10 х 2 = — 3 (не входит в ОДЗ)
2) 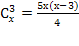

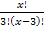
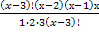
4х(х-2)(х-1) = 6
х(4х 2 – 12х+8-30х+90)=0
х=0 или 4х 2 – 42х + 98 = 0
2х 2 – 21х + 49 = 0
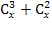

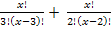
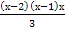
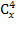
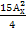

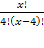
4(х-2)! = 24
х 1 =12; х 2 = — 7(не входит в ОДЗ)
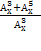

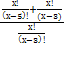
х 1 =10; х 2 = 3 (не входит в ОДЗ)
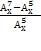

х 2 – 11х – 60 = 0
х 1 =15; х 2 = — 4(не входит в ОДЗ)
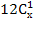
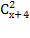

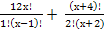
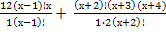
2
24х + х 2 + 7х + 12 – 324 = 0
х 2 + 31х – 312 = 0
х 1 =8; х 2 = — 39(не входит в ОДЗ)
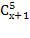
ОДЗ: 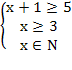
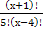
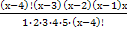
(х-2)(х-1)х = 0 или (х-3)-45 = 0
х 1 =2; х 2 = 1 х 3 =0 — не входят в ОДЗ х 4 = 48
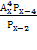

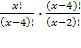
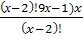
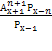
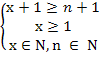
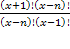
х 1 =10; х 2 = — 9(не входит в ОДЗ)
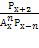
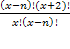
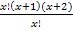
x 2 +3 x +2–132 = 0
х 1 =10; х 2 = — 13(не входит в ОДЗ)
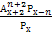
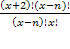
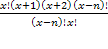
x 2 +3 x +2– 110 = 0
x 2 +3 x – 108 = 0
х 1 =9; х 2 = — 12(не входит в ОДЗ)
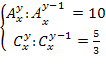
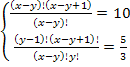
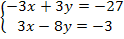
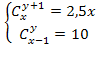
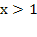
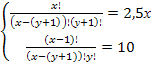
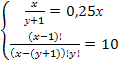
(х-3)(х-2)(х-1) = 3
4)
Сколько двузначных чисел можно составить из цифр 1. 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр?
Из 6 открыток надо выбрать 3. Сколькими способами это можно сделать?
http://poformule.ru/matematika/kombinatorika
http://urokimatematiki.ru/konspekt-uroka-na-temu-reshenie-kombinatornih-uravneniy-klass-5297.html