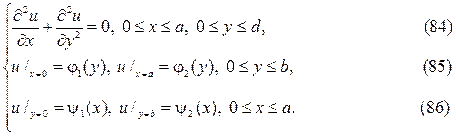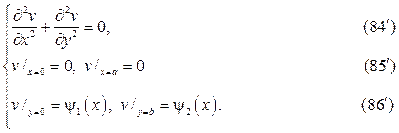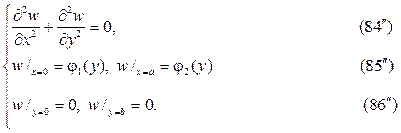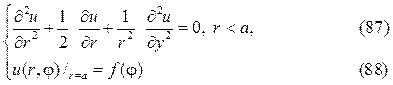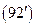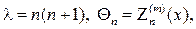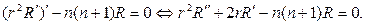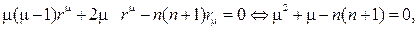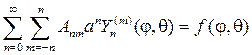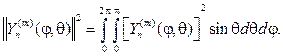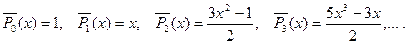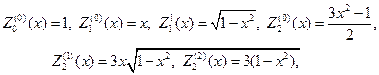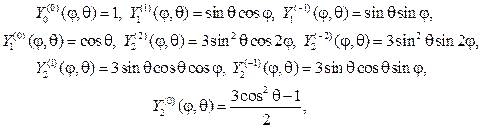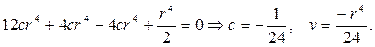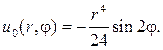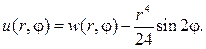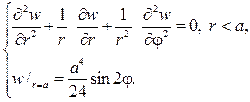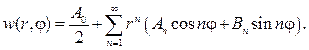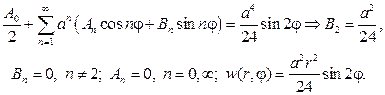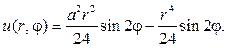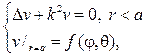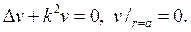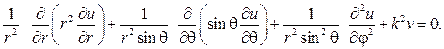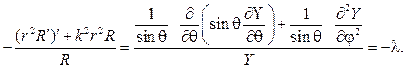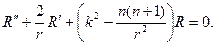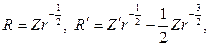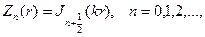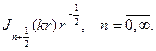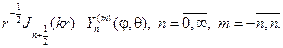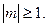Решить краевую задачу для уравнения гельмгольца в круге

Решить краевую задачу для уравнения гельмгольца в круге

Настоящая книга является естественным дополнением пособия А. Г. Свешникова, А. Н. Боголюбова, В. В. Кравцова «Лекции по математической физике». Её основная цель — помочь студентам приобрести необходимые практические навыки исследования математических моделей физических явлений, являющихся краевыми или начально-краевыми задачами для линейных дифференциальных уравнений в частных производных второго порядка. С этой целью каждая глава пособия построена следующим образом. В начале каждого параграфа главы приводятся необходимые минимальные сведения теоретического характера, используемые для решения данного типа задач. Затем эти методы демонстрируются в работе, для чего даются примеры решения конкретных задач. В конце главы приводятся задачи с ответами для самостоятельного решения.

Содержание пособия полностью соответствует курсу «Методы математической физики», читаемому на физическом факультете МГУ. Пособие написано на основе более чем двадцатилетнего опыта преподавания на физическом факультете Московского университета. Оно рассчитано в первую очередь на студентов физических специальностей университетов, но будет полезно и студентам инженерных специальностей и лицам, занимающимся математической физикой и прикладной математикой.

Авторы выражают свою глубокую благодарность заведующему кафедрой Московского государственного института электронной профессору А. С. Поспелову, профессорам А. В. Ефимову, А. С. Ильинскому и С. Я. Секерж-Зеньковичу, взявшим на себя труд ознакомиться с рукописью и сделавшим ряд ценных замечаний.

МЕТОД РАЗДЕЛЕНИЯ ДЛЯ УРАВНЕНИЙ

ЭЛЛИПТИЧЕСКОГО ТИПА

Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма Лиувилля своеобразны, их граничные ус- ловия определяются спецификой областей:

следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач

Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.

Рассмотрим задачу Дирихле для круга

где f(j)кусочно-непрерывная функция.

Следуя схеме метода Фурье полагаем

подставляем в (87) и разделяем переменные. В результате получим ра -венство

(90)

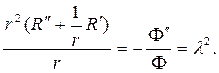
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма Лиувилля

откуда следует, что

(91)

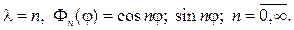
Возвращаясь к (80), решаем уравнение для радианальной функции. При

r 2 R² + rR¢ n 2 R = 0,

решение следует искать в виде степенной функции R=r m . Для определе- ния m получим соотношение

m(m 1)r m +m r m n 2 r m =0Û m 2 n 2 =0,

Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции

R₀(r) = 1; lnr.

С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге

Если предположить, что ряд

(93)

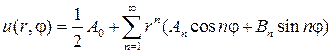
можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем

(94)

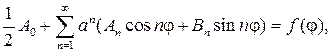
откуда с учетом формул коэффициентов Фурье следует

(95)

(96) Итог состоит в том, что решение задачи (87 88) дается рядом (93), коэффициенты которого определены равенствами (95-96).

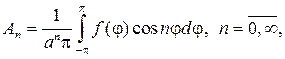
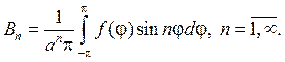
Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r — n и lnr, поскольку они разрывны в

центре круга r=0.

Напротив, если рассматривать область r>a, то нельзя привлекать r — n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом

(97)

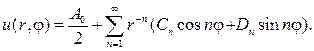
В случае кругового кольца a 2 q= 1-x 2 , найдем

(104¢)

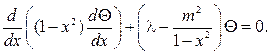
Соответственно и граничные условия (105) перейдут после замены в неравенства

(105′)

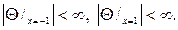
Задача (104¢) (105¢) есть известная задача для присоединенных функций Лежандра, ее решение (см., например, [3], стр. 115)

и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):

(106)

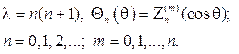
Составив произведения функций (106) на найденные выше функции F_m(j), получим множество решений уравнения (102)

(107)

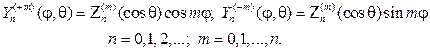
Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.

Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m₁¹m₂ или n₁¹n₂

(108)

Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции

Оно имеет решение в виде степенной функции R=r m . Действительно, после подстановки

откуда находим значения m=n; (n+1) и соответственно решения

(109)

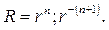
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:

Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами

(110)

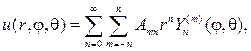
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.

Для нахождения коэффициентов А_nm подставим (110) в (100), тогда

и с учетом (108) найдем

(111)

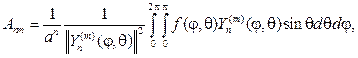
Последний интеграл вычисляется и при m=0 :

(112)

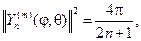
если же |m| ³ 1, то имеем

(113)

Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).

Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам

(114)

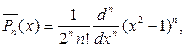
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.

(115)

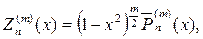
в частности будем иметь

(116)

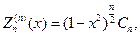
где С_n определенная константа.

С учетом (107), (115) и (116) выпишем несколько сферических функций:

(117)

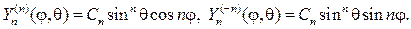
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд

(118)

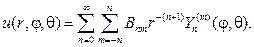
Общий вид гармонической функции в шаровом слое a 4 , и получим

Таким образом, частным решением будет функция

Вводим новую неизвестную функцию w(r,j) , полагая

Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа

Согласно (93), решение этой задачи дается формулой

Подставляя ее в граничное условие, получим

Ответом в задаче будет функция

254. Найдите решение первой краевой задачи для уравнения Гельмгольца

предполагая, что k не является собственным значением задачи

Р е ш е н и е. Запишем уравнение в сферических координатах

Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:

Функция 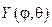будет решением уравнения (72), которое нужно решать при условии ограниченности и 2p-периодичности по j. В результате при- дем к сферическим функциям при l=n(n+1):

Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение

Выполняя в этом уравнении замену

придем к соотношению относительно новой функции Z(r):

Последнее уравнение в качестве ограниченных в окрестности нуля

r=0 решений имеет бесселевы функции

соответственно будем иметь набор радиальных функций

Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:

Составляем ряд с числовыми коэффициентами

(119)

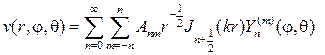
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a

где d = 4 при m = 0 и d =2 при

При найденных коэффициентах A_nm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.

255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1

ТЕМА: Уравнения эллиптического типа

ТИТУЛЬНЫЙ ЛИСТ

1 Теоретические обоснования уравнений эллиптического типа………………. 4

1.1. Задачи приводящие к уравнению Лапласа………………. 5

1.2. Уравнение Шредингера и его стационарный аналог. 9

1.3. Уравнение Гельмгольца……………………………………………. ……10

2 Примеры решения задач на уравнения эллиптического типа……………………12

Список использованных источников……………………………………………. …16

В курсовой работе будут рассмотрены уравнения эллиптического типа.

Актуальность исследования заключается в том, что благодаря данному типу уравнений можно описать стационарные процессы, проходящие в различных физических полях. Например, с помощью уравнения Пуассона можно описать электростатическое поле, поле давления [1].

Исследование затронет следующие проблемы: применение уравнений эллиптического типа на практике и способы их решения.

Целью исследования является: изучение вопроса, касающегося применения уравнений эллиптического типа на практике.

Основными задачами, поставленными для достижения цели можно считать:

— ознакомиться с положениями, характеризующими уравнения эллиптического типа;

— выявить основные уравнения, относящиеся к данному типу;

— освоить навык решения задач, используя данные уравнения;

— показать специфику проблем, которые могут возникнуть на этапах решения.

Объектом исследования заданной темы являются дифференциальные уравнения в частных производных.

Предметом исследования выступают уравнения эллиптического типа.

Теоретической и методологической основой исследования послужили труды отечественных и зарубежных деятелей, методические пособия по дисциплине «методы математической физики».

1. ТЕОРЕТИЧЕСКИЕ ОБОСНОВАНИЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА

Помимо физических явлений, развивающихся в пространстве и во времени, существует множество процессов, которые не изменяются с течением времени. Эти процессы называются стационарными. При исследовании данных процессов, различной физической природы (колебания, теплопроводность, диффузия и др.) обычно приходят к уравнениям эллиптического типа. Примерами могут выступать:

1. Уравнения Лапласа и Пуассона, описывают различные стационарные физические поля.

2. Стационарный аналог уравнения Шредингера, когда предполагается гармоническая зависимость от времени.

3. Уравнение Гельмгольца.

4. Уравнения, получаемые из уравнения Максвелла, если предполагается, что электромагнитное поле не изменяется с течением времени [1].

Наиболее распространенным уравнением этого типа является уравнение Лапласа

.

Этим уравнением характеризуется гравитационный и электростатический потенциалы в точках свободного пространства, оно описывает потенциал скорости безвихревого потока несжимаемой жидкости, и оно же справедливо для температуры однородной изотропной среды при установившемся движении тепла.

Функция называется гармонической в области , если она непрерывна в этой области вместе со своими производными до 2-го порядка и удовлетворяют уравнению Лапласа.

При изучении свойств гармонических функций были разработанные различные математические методы, оказавшиеся плодотворными и в применении к уравнениями гиперболического и параболического типов [1].

1.1. ЗАДАЧИ ПРИВОДЯЩИЕ К УРАВНЕНИЮ ЛАПЛАСА

1. Стационарное тепловое поле. Постановка краевых задач.

Рассматривается стационарное тепловое поле. Температура нестационарного теплового может быть представлена дифференциальным уравнением теплопроводности

Если процесс стационарен, то устанавливается распределение температуры , не меняющееся с течением времени и, следовательно, удовлетворяющее уравнению Лапласа

(1)

При наличии источников тепла получается уравнение

(2)

где – плотность тепловых источников, а – коэффициент теплопроводности. Неоднородное уравнение Лапласа (2) часто называют уравнением Пуассона.

Рассматривается некоторый объем , ограниченный поверхностью . Задача о стационарном распределении температуры внутри тела формулируется следующим образом:

Найти функцию , удовлетворяющую внутри Т уравнению

,

(3)

и граничному условию, которое может быть взято в одном из следующих видов:

I. на (первая краевая задача);

II. на (вторая краевая задача);

III. на (третья краевая задача).

где , , , — заданные функции, – производная по внешней нормали к поверхности

Первую краевую задачу называют для уравнений Лапласа часто называют задачей Дирехле, а вторую задачу – задачей Неймана.

Если ищется решение в области , внутренней (или внешней) по отношению к поверхности , то соответствующую задачу называют внутренней (или внешней) краевой задачей [3].

2. Потенциальное течение жидкости. Потенциал стационарного тока и электростатического поля.

В качестве второго примера будет рассмотрено потенциальное течение жидкости без источников. Пусть внутри некоторого объема с границей имеет место стационарное течение несжимаемой жидкости (плотность ), характеризуемое скоростью . Если течение жидкости не вихревое, то скорость является потенциальным вектором, т.е

(4)

где – скалярная функция, называемая потенциалом скорости. Если отсутствуют источники, то

.

(5)

При подстановке сюда выражения (3) для υ, выходит:

,

,

(6)

то есть потенциал скорости удовлетворяет уравнению Лапласа.

Пусть в однородной проводящей среде имеется стационарный ток с объемной плотностью . Если в среде нет объемных источников тока, то

.

(7)

Электрическое поле определяется через плотность тока из дифференциального закона Ома

(8)

где – проводимость среды.

Поскольку процесс стационарный, то электрическое поле является безвихревым или потенциальным, т.е. существует такая скалярная функция для которой

).

(9)

Отсюда на основании формул (6) и (7) заключается, что

,

(10)

т.е. потенциал электрического поля стационарного тока удовлетворяет уравнению Лапласа.

Рассматривается электрическое поле стационарных зарядов. Из стационарности процесса следует, что

,

(11)

т.е. поле является потенциальным и

.

Пусть – объемная плотность заряда, имеющихся в среде, характеризуемой диэлектрической постоянной .

Исходя из основного закона электродинамики

(12)

где – некоторый объем, – поверхность, его ограничивающая, где – сумма всех зарядов внутри , и пользуясь теоремой Отроградского

(13)

.

При подстановке сюда выражение (8) для , выходит:

,

(14)

т.е. электростатический потенциал удовлетворяет уравнению Пуассона. Если объемных зарядов нет , то потенциал должен удовлетворять уравнению Лапласа

Нами был рассмотрен ряд процессов. Основные краевые задачи для которых относятся к трем типам, приведенным выше [1].

1.2. УРАВНЕНИЕ ШРЕДИНГЕРА И ЕГО СТАЦИОНАРНЫЙ АНАЛОГ

В квантовой механике состояние частицы описывается волновой функцией , квадрат модуля которой имеет смысл плотности вероятности найти частицу в окрестности данной точки в момент времени [2]. Волновая функция удовлетворяет уравнению Шредингера

где — постоянная Планка. Оператор Гамильтона для движения частицы в поле имеет вид

Уравнение Шредингера является уравнением в частных производных второго порядка по координатам, но первого порядка по времени. В отличие от волнового уравнения, чтобы выделить частное решение из общего, надо задавать при одно начальное условие, а не два.

Если искать решение в виде стационарных состояний , имеющих определенную энергию , то время можно исключить и получить стационарное уравнение Шредингера

(15)

Требуется найти не только решение , но и такие значения энергии , при которых эти решения удовлетворяют граничным условиям. Такая постановка называется спектральной задачей [3].

1.3 УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА

Эллиптическое дифференциальное уравнение в частных производных, получаемое из уравнение Максвелла, если предполагается, что электромагнитное поле либо не меняется с течением времени, либо меняется по гармоническому закону. Может быть представлено как

где – это оператор Лапласа, а неизвестная функция определена в (на практике уравнение Гельмгольца применяется для ).

В уравнение Гельмгольца не входят операторы дифференцирования по времени, следовательно, сведение исходной задачи в частных производных к уравнению Гельмгольца может упростить её решение. Для примера рассматривается волновое уравнение:

(16)

Пусть функции и допускают разделение переменных: , и пусть . Нужно заметить, что в пространстве Фурье – преобразований дифференцирование по времени соответствует умножению на множитель . Таким образом, уравнение приводится к виду:

(17)

где = — это квадрат модуля волнового вектора.

Решение уравнения Гельмгольца зависит от вида граничных условий. В двумерном случае уравнение Гельмгольца применяется для решения задачи о колеблющейся мембране, тогда естественным образом задаются однородные граничные условия, что физически соответствует закреплению мембраны на границе. В таком случае решение будет зависеть от формы мембраны. Так, для круглой мембраны радиуса в полярных координатах уравнение принимает вид:

(18)

Метод разделения переменных позволяет перейти к задаче на собственные значения для части решения, зависящей только от :

(19)

(20)

а функция, зависящая только от радиуса, будет удовлетворять уравнению:

(21)

Фундаментальными решениями этих уравнений являются, соответственно, функции , где – i-корень функции Бесселя λ-го порядка [4].

2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА

В отличие от смешанных задач, для эллиптических уравнений ставится только краевая задача

где – внешняя нормаль к границе области .

При этом, если , задача называется задачей Дирихле, если , задачей Неймана, если то задача называется смешанной.

Задачи буду решаться в полярных или сферических координатах. Заданные краевые условия произвольные, неоднородные. Однородные краевые условия для нахождения собственных функций возникают из-за того, что области имеют специальный вид, а потому решение должно иметь период , а в случае прибавляются условия (уравнение Лапласа в новых координатах при этом имеет особенность). [5].

Предлагаю рассмотреть метод нахождения решения уравнения Лапласа в круге, то есть метод нахождения функции , удовлетворяющий уравнению Лапласа внутри круга радиусом c центром в полюсе полярной системы координат и граничному условию на окружности

где – заданная функция, непрерывная на окружности.

Задача № 1. Решить краевую задачу для уравнения в круге , если на границе круга φ.

Решение: Уравнение Лапласа в полярных координатах имеет вид

(22)

1. Частное решение уравнения в соответствии с методом Фурье ищется в виде

причем и периодическая с периодом

При подстановке в уравнение (22) и разделяя переменные, выходит

Поэтому функции и являются решениями связанных задач:

a)

b)

2. Решается задача

Общее решение уравнения имеет вид

(23)

где и – константы.

Это решение периодично при и имеет период при

Если

Если

3. Решается задача

Если Общее решение этого уравнения

Так как

Если ,

Общее решение этого уравнения

Так как

4. Вспомогательные решения имеют вид:

5. Тогда решение исходной задачи ищется в виде

6. При использовании граничного условия sin3φ,

получается sin3φ. Отсюда

В результате

Ответ:

Задача № 2. Решить краевую задачу

Решение: Проводятся преобразования, аналогичные предыдущей задачи до момента нахождения коэффициентов .

Нужно представить граничное условие в виде

Следовательно,

Далее предлагаю рассмотреть примеры решения краевых задач уравнения Гельмгольца.

Задача № 3. Решить краевую задачу для уравнения Гельмгольца в круге

(здесь , где – собственное значение однородной задачи Дирехле для уравнения ).

Решение: Используя метод разделения переменных (метод Фурье). Полагая, и подставляя предполагаемую форму решения в Уравнении Гельмгольца, получается

где – постоянная разделения.

Собственные значения и собственные функции определяются как решения данной задачи:

Выходит

то для определения получается уравнение

(24)

Обозначив , переписывается уравнение (24) в виде

Это уравнение Бесселя порядка . Его общее решение есть

где – функция Бесселя первого рода порядка – функция Бесселя второго рода порядка – произвольные постоянные.

Значит, решение уравнения (1) имеет вид

Поскольку и имеется дело с ограниченными решениями, то полагаем Таким образом, . Решение нашей задачи представляется рядом

(25)

Постоянные находятся из граничного условия. Полагая в (25) , получаем

В частности, при выходит

и в этом случае решение имеет вид

В проделанной нами работе, мы акцентировали внимание на такой теме как «Уравнения эллиптического типа». В ходе нашего исследования мы сумели выполнить поставленные перед нами задачи, что повлекло за собой достижение цели работы. Изучив теоретические материалы, мы разобрались с основными уравнениями, научились выводить их и применять в решениях задач. Были обозначены проблемы и пути их решения. В качестве примера выступили три задачи, требующие решение эллиптического уравнения.

Материалом данного исследования выступали труды советских и российских деятелей, содержащие в себе подробную информацию, касающуюся нашей проблемы.

В ходе выполнения данной работы появилась возможность оценить важность заданной темы в современной науке, определить основные задачи, которые можно решать с помощью уравнений эллиптического типа.

Подводя итог, хочется отметить, что изучение данного вопроса способствовала возникновению большого интереса, что позволило с энтузиазмом продолжать с ознакомлением трудов знаменитых авторов для дальнейшего анализа и использования в работе.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.А.Н. Тихонов, А.А. Самарский, Уравнения математической физики М., издательство «наука», 1977. – 735 с.

2. Л.Д. Ландау, Е. М. Лифшиц, Квантовая механика,
М., Изд. 4е, «Наука», 1989. – 767 с.

3. Д.А. Шапиро, Конспект лекций по методам математической физики ч.1, кафедра теоретической физики НГУ, 2004. – 123 с.

4. В. С. Владимиров, В. В. Жаринов, Уравнения математической физики. — М.: «Физматлит», 2004. – 400 с.

5. С.И. Колесникова, Методы решения основных задач уравнений математической физики, М., МФТИ, 2015. – 80 с.