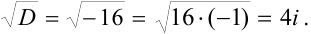Решить квадратное уравнение отрицательный дискриминант

Решение квадратных уравнений с отрицательным дискриминантом

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:

Пример №42.4.

Решить уравнение: .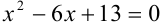

Решение:

Найдем дискриминант: .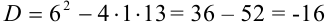

Тогда .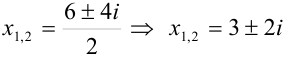

Ответ: .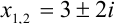

Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.

Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение -й степени имеет комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Другие лекции по высшей математике, возможно вам пригодятся:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Дискриминант

Дискриминантом квадратного трехчлена называют выражение \(b^<2>-4ac\), где \(a, b\) и \(c\) – коэффициенты данного трехчлена.

Например, для трехчлена \(3x^2+2x-7\), дискриминант будет равен \(2^2-4\cdot3\cdot(-7)=4+84=88\). А для трехчлена \(x^2-5x+11\), он будет равен \((-5)^2-4\cdot1\cdot11=25-44=-19\).

Дискриминант обозначается буквой \(D\) и часто используется при решении квадратных уравнений . Также по значению дискриминанта можно понять, как примерно выглядит график квадратичной функции (см. ниже).

Дискриминант и корни квадратного уравнения

Значение дискриминанта показывает количество корней квадратного уравнения:
— если \(D\) положителен – уравнение будет иметь два корня;
— если \(D\) равен нулю – только один корень;
— если \(D\) отрицателен – корней нет.

Это не надо учить, к такому выводу несложно прийти, просто зная, что квадратный корень из дискриминанта (то есть, \(\sqrt\) входит в формулу для вычисления корней квадратного уравнения: \(x_<1>=\) \(\frac<-b+\sqrt><2a>\) и \(x_<2>=\) \(\frac<-b-\sqrt><2a>\) . Давайте рассмотрим каждый случай подробнее.

Если дискриминант положителен

В этом случае корень из него – это некоторое положительное число, а значит \(x_<1>\) и \(x_<2>\) будут различны по значению, ведь в первой формуле \(\sqrt\) прибавляется, а во второй – вычитается. И мы имеем два разных корня.

Пример: Найдите корни уравнения \(x^2+2x-3=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Найдем корни уравнения

Получили два различных корня из-за разных знаков перед \(\sqrt\)

На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение \(x^2+2x-3=0\) имеет корни \(x_<1>=1\) и \(x_<1>=-3\), значит при подстановке \(1\) и \(-3\) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию \(y=x^2+2x-3\) получим \(y=0\). То есть, функция \(y=x^2+2x-3\) проходит через точки \((1;0)\) и \((-3;0)\) (подробнее смотри статью Как построить график функции ).

Если дискриминант равен нулю

А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.

Формулы корней выглядят так: \(x_<1>=\) \(\frac<-b+\sqrt><2a>\) и \(x_<2>=\) \(\frac<-b-\sqrt><2a>\) . И если дискриминант – ноль, то и корень из него тоже ноль. Тогда получается:

То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.

Пример: Найдите корни уравнения \(x^2-4x+4=0\)
Решение:

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.

На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция \(y=x^2-4x+4\) будет выглядеть вот так:

Если дискриминант отрицателен

В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.

Пример: Найдите корни уравнения \(x^2+x+3=0\)
Решение

Вычисляем дискриминант по формуле \(D=b^2-4ac\)

Находим корни уравнения

Оба корня содержат невычислимое выражение \(\sqrt<-11>\), значит, и сами не вычислимы

То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение \(x^2+x+3\) получился ноль.

Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.

Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение квадратного уравнения.

С помощью этой математической программы вы можете решить квадратное уравнение.

Программа не только даёт ответ задачи, но и отображает процесс решения двумя способами:
— с помощью дискриминанта
— с помощью теоремы Виета (если возможно).

Причём, ответ выводится точный, а не приближенный.
Например, для уравнения \(81x^2-16x-1=0\) ответ выводится в такой форме:

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода квадратного многочлена, рекомендуем с ними ознакомиться.

В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5z +1/7z^2
Результат: \( 3\frac<1> <3>— 5\frac<6> <5>z + \frac<1><7>z^2 \)

При вводе выражения можно использовать скобки. В этом случае при решении квадратного уравнения введённое выражение сначала упрощается.
Например: 1/2(y-1)(y+1)-(5y-10&1/2)

Немного теории.

Квадратное уравнение и его корни. Неполные квадратные уравнения

Каждое из уравнений
\( -x^2+6x+1<,>4=0, \quad 8x^2-7x=0, \quad x^2-\frac<4><9>=0 \)
имеет вид
\( ax^2+bx+c=0, \)
где x — переменная, a, b и c — числа.
В первом уравнении a = -1, b = 6 и c = 1,4, во втором a = 8, b = —7 и c = 0, в третьем a = 1, b = 0 и c = 4/9. Такие уравнения называют квадратными уравнениями.

Определение.
Квадратным уравнением называется уравнение вида ax 2 +bx+c=0, где x — переменная, a, b и c — некоторые числа, причём \( a \neq 0 \).

Числа a, b и c — коэффициенты квадратного уравнения. Число a называют первым коэффициентом, число b — вторым коэффициентом и число c — свободным членом.

В каждом из уравнений вида ax 2 +bx+c=0, где \( a \neq 0 \), наибольшая степень переменной x — квадрат. Отсюда и название: квадратное уравнение.

Заметим, что квадратное уравнение называют ещё уравнением второй степени, так как его левая часть есть многочлен второй степени.

Квадратное уравнение, в котором коэффициент при x 2 равен 1, называют приведённым квадратным уравнением. Например, приведёнными квадратными уравнениями являются уравнения
\( x^2-11x+30=0, \quad x^2-6x=0, \quad x^2-8=0 \)

Если в квадратном уравнении ax 2 +bx+c=0 хотя бы один из коэффициентов b или c равен нулю, то такое уравнение называют неполным квадратным уравнением. Так, уравнения -2x 2 +7=0, 3x 2 -10x=0, -4x 2 =0 — неполные квадратные уравнения. В первом из них b=0, во втором c=0, в третьем b=0 и c=0.

Неполные квадратные уравнения бывают трёх видов:
1) ax 2 +c=0, где \( c \neq 0 \);
2) ax 2 +bx=0, где \( b \neq 0 \);
3) ax 2 =0.

Рассмотрим решение уравнений каждого из этих видов.

Для решения неполного квадратного уравнения вида ax 2 +c=0 при \( c \neq 0 \) переносят его свободный член в правую часть и делят обе части уравнения на a:
\( x^2 = -\frac \Rightarrow x_ <1,2>= \pm \sqrt< -\frac> \)

Так как \( c \neq 0 \), то \( -\frac \neq 0 \)

Значит, неполное квадратное уравнение вида ax 2 +bx=0 при \( b \neq 0 \) всегда имеет два корня.

Неполное квадратное уравнение вида ax 2 =0 равносильно уравнению x 2 =0 и поэтому имеет единственный корень 0.

Формула корней квадратного уравнения

Рассмотрим теперь, как решают квадратные уравнения, в которых оба коэффициента при неизвестных и свободный член отличны от нуля.

Решим квадратне уравнение в общем виде и в результате получим формулу корней. Затем эту формулу можно будет применять при решении любого квадратного уравнения.

Решим квадратное уравнение ax 2 +bx+c=0

Разделив обе его части на a, получим равносильное ему приведённое квадратное уравнение
\( x^2+\fracx +\frac=0 \)

Преобразуем это уравнение, выделив квадрат двучлена:
\( x^2+2x \cdot \frac<2a>+\left( \frac<2a>\right)^2- \left( \frac<2a>\right)^2 + \frac = 0 \Rightarrow \)

Подкоренное выражение называют дискриминантом квадратного уравнения ax 2 +bx+c=0 («дискриминант» по латыни — различитель). Его обозначают буквой D, т.е.
\( D = b^2-4ac \)

Теперь, используя обозначение дискриминанта, перепишем формулу для корней квадратного уравнения:
\( x_ <1,2>= \frac < -b \pm \sqrt> <2a>\), где \( D= b^2-4ac \)

Очевидно, что:
1) Если D>0, то квадратное уравнение имеет два корня.
2) Если D=0, то квадратное уравнение имеет один корень \( x=-\frac <2a>\).
3) Если D 0), один корень (при D = 0) или не иметь корней (при D

Теорема Виета

Приведённое квадратное уравнение ax 2 -7x+10=0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Мы видим, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Таким свойством обладает любое приведённое квадратное уравнение, имеющее корни.

Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Т.е. теорема Виета утверждает, что корни x₁ и x₂ приведённого квадратного уравнения x 2 +px+q=0 обладают свойством:
\( \left\< \begin x_1+x_2=-p \\ x_1 \cdot x_2=q \end \right. \)