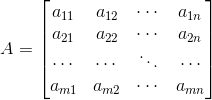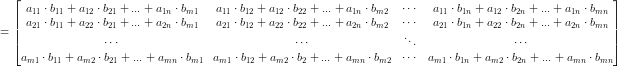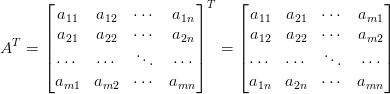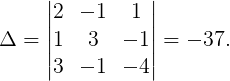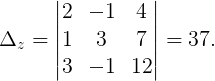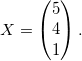Линейная алгебра
Линейная алгебра – специализированный раздел математики, предназначенный для изучения алгебраическими методами при помощи матриц, сопряжений и определителей систем линейных уравнений, линейных и векторных пространств.
Методы линейной алгебры являются универсальными, они применяются при решении задач, относящихся к другим разделам математики. В частности, в функциональном анализе в применении к линейным пространствам с особыми бесконечномерными свойствами задействуются не только методики математического анализа, но и инструментарий линейной алгебры.
Линейная алгебра находит применение в эконометрике, квантовой механике и иных естественных науках. Ее методы с увеличением технических возможностей компьютерной техники все более широко используются в линейном программировании различных приложений, используемых при решении разнообразных производственных, транспортных, логистических и иных практических задач.
Решение задач по линейной алгебре
| Срок выполнения | от 1 дня |
| Цена | от 50 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
Линейная алгебра: определение, объекты, инструменты
Линейная алгебра – это раздел алгебры, в котором изучаются объекты линейной природы, в частности:
- линейные отображения;
- векторные пространства;
- системы линейных уравнений.
Истоки элементов линейной алгебры относятся к временам Евклида. Различные методы линейной алгебры применялись также у древних вавилонян и древних китайцев.
Основными инструментами, которые применяются в линейной алгебре, являются матрицы, определители матриц, а также сопряжение.
Изучение перечисленных выше объектов образует соответствующие разделы линейной алгебры. Не секрет, что наиболее простым будет раздел, в котором изучаются системы линейных уравнений, методы их решения. Линейные отображения и векторные пространства более сложны для изучения и понимания и, как правило, изучаются на физико-математических факультетах.
Изучение систем линейных уравнений и методов их решения включает рассмотрение следующих понятий:
- матрицы;
- определители;
- операции над матрицами;
- системы линейных алгебраических уравнений (СЛАУ), их виды;
- методы решения СЛАУ.
В данной статье остановим свое внимание именно на выделенном разделе линейной алгебры. Однако не будем сильно вдаваться в теорию, поскольку данная статья не является учебником по линейной алгебре; рассмотрим кратко и только основное, чтобы иметь первоначальное представление о том, с чем приходится иметь дело.
Линейная алгебра: основные понятия и формулы
Матрица – это система элементов (функций, чисел и др. величин), которые расположены в виде прямоугольной таблицы. Общий вид записи матрицы представлен ниже:
Произвольный элемент матрицы обозначается через aij (элемент i-й строки и j-го столбца). Тем, кто знаком с основами алгоритмизации и программирования, будет проще, если сравнить матрицу с двумерным массивом данных (в частном случае с одномерным массивом). Матрица имеет размерность, определяемую количеством строк и столбцов.
Основными действиями над матрицами являются:
- сравнение (для матриц одинаковой размерности):
- сложение и вычитание (для матриц одинаковой размерности):
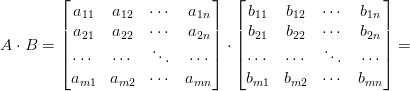
- умножение (количество столбцов первой матрицы равно количеству строк второй матрицы):
- транспонирование:
- обращение:
При нахождении обратной матрицы появляются определитель и алгебраические дополнения, подробнее о которых можно прочитать в любом учебнике по линейной алгебре.
Итак, зная перечисленные формулы, можно смело приступать к их применению, например, при решении СЛАУ вида:
где 
При решении систем линейных уравнений, как правило, используют следующие методы:
- метод Крамера (или формулы Крамера);
- метод Гаусса (реже метод Жордана-Гаусса);
- метод обратной матрицы.
Метод Крамера основан на вычислении определителей матриц, название метода обратной матрицы говорит само за себя. Оба метода применяются в основном при решении систем двух (трех) уравнений с двумя (тремя) неизвестными, что связано с проблематичностью и громоздкостью вычислений определителей и обратных матриц размерности больше трех.
В отличие от предыдущих методов метод Гаусса достаточно легко применяется и для систем с большим числом неизвестных.
В данной статье не будем рассматривать теорию перечисленных методов, а представление о них дадим на соответствующих примерах.
Линейная алгебра: примеры решения задач
Рассмотрим несколько простейших задач из курса линейной алгебры.
Пример 1. Вычислить определитель а) по формуле Саррюса и б) путем разложения по элементам строки: 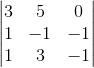
Решение:
а)
б) 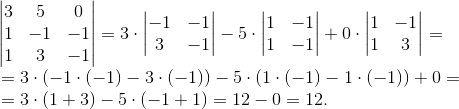
Ответ: Δ = 12 .
Пример 2. Даны две матрицы 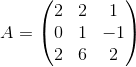
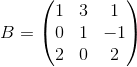
Решение: 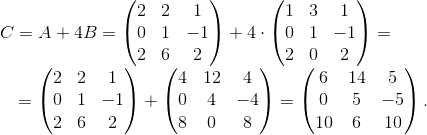
Ответ: 
Пример 3. Решить СЛАУ, используя формулы Крамера: 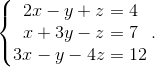
Решение:
Формулы Крамера:
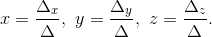
Вычислим все необходимые определители:
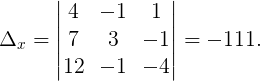
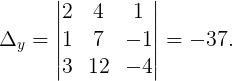
Следовательно, 
Ответ: x = 3 , y = 1 , z = -1 .
Пример 4. Решить СЛАУ методом обратной матрицы: 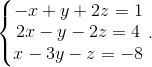
Решение:
Запишем систему уравнений в матричном виде:
AX = B , где
Решение уравнения найдем по формулам:
Найдем обратную матрицу:

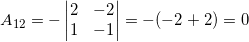




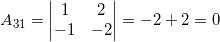



Ответ:
Заключение
Здесь будет правильным привести примерный список учебников для изучения курса линейной алгебры:
- Ильин В.А., Позняк Э.Г. Линейная алгебра: Учеб. Для вузов – 4-е изд. – М. Наука, 1999. – 296 с.
- Мальцев А. И., Основы линейной алгебры, 3-е изд. – М.: Наука, 1970.
Решение линейной алгебры на заказ
Заказать решение задач по линейной алгебре можно здесь. Достаточно просто заполнить форму заказа.
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
http://reshatel.org/reshenie-zadach/reshenie-zadach-po-linejnoj-algebre/
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij