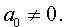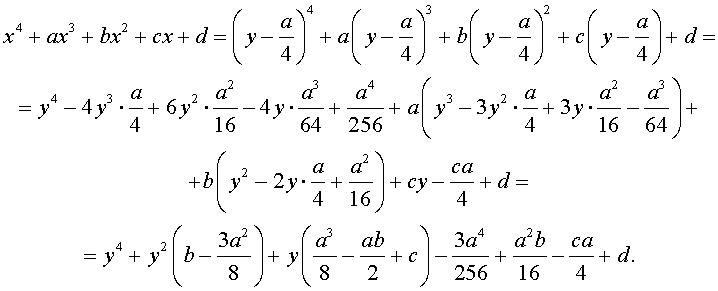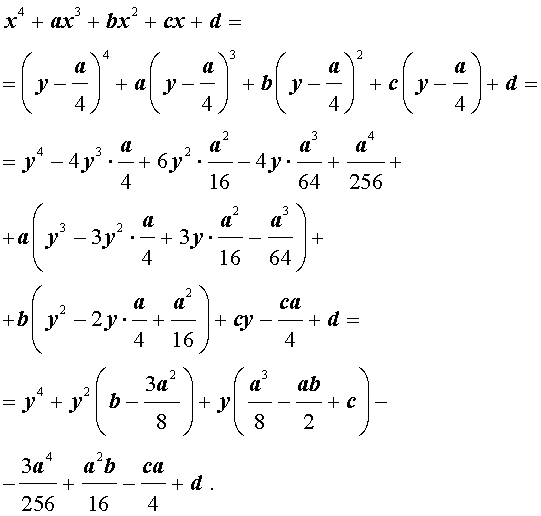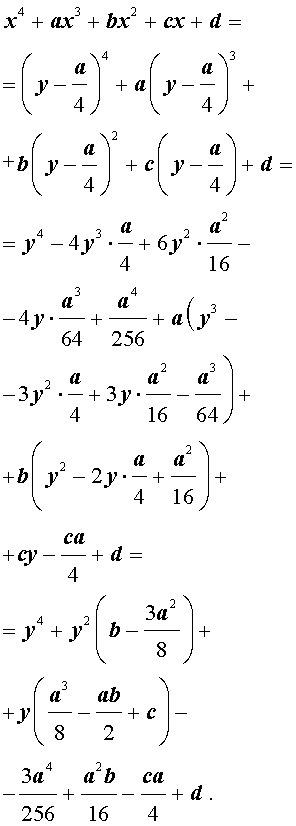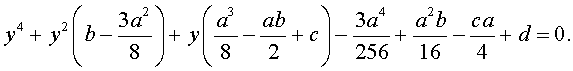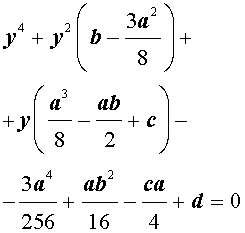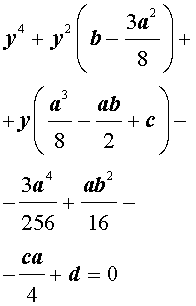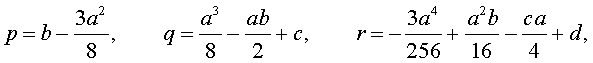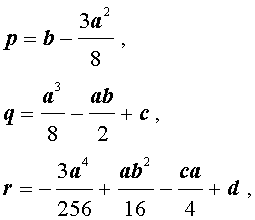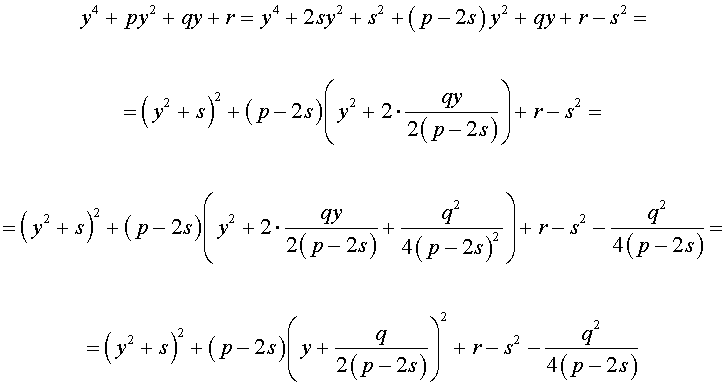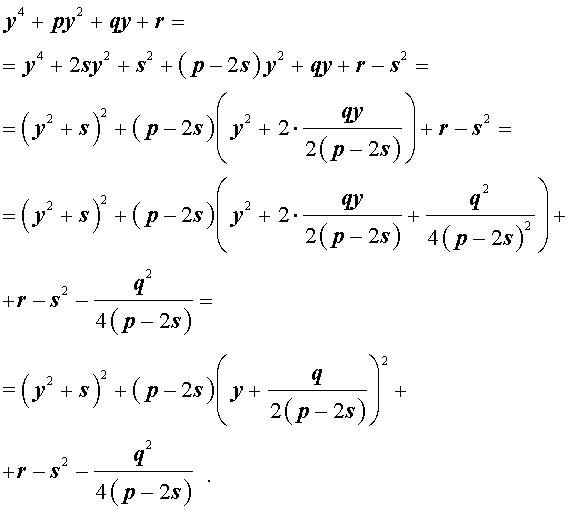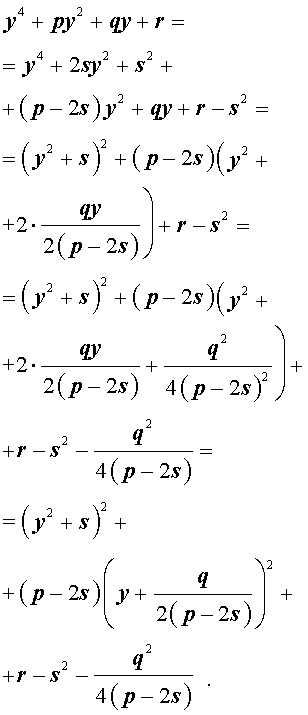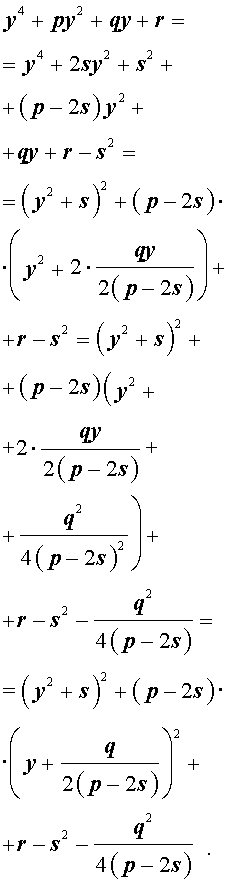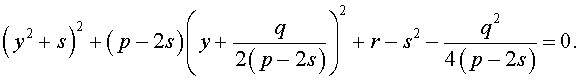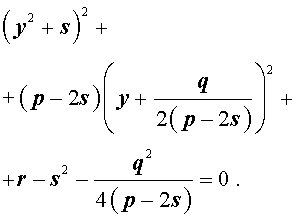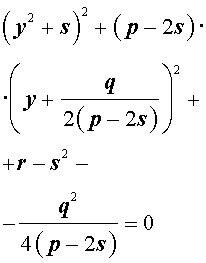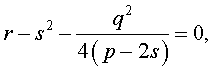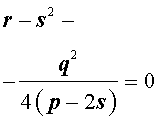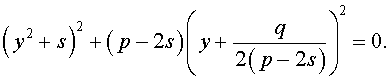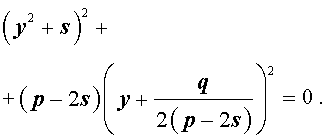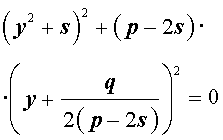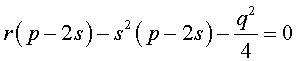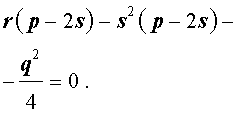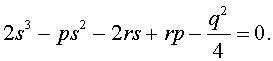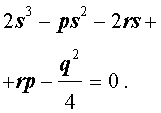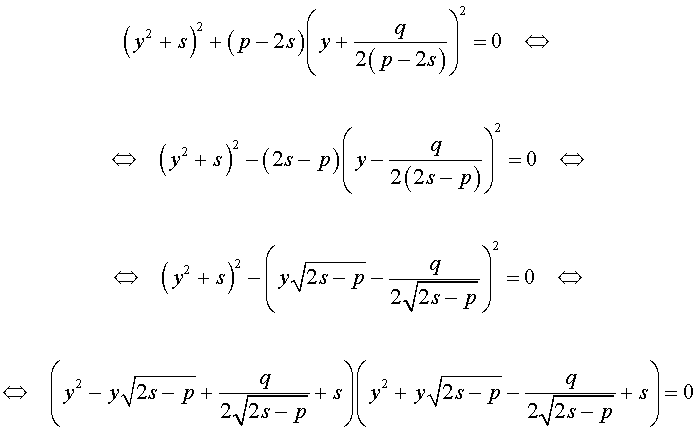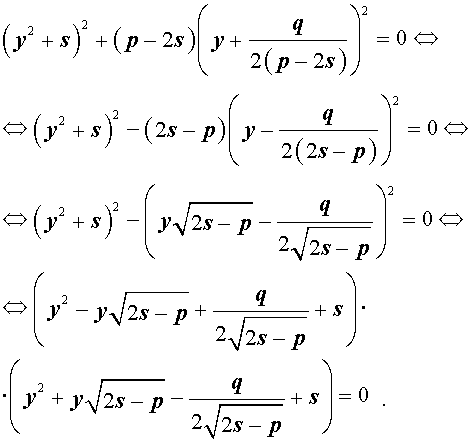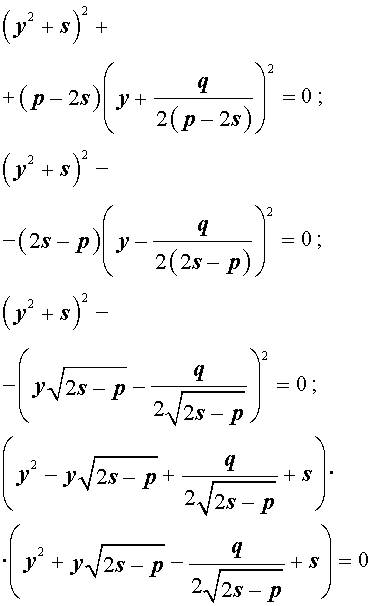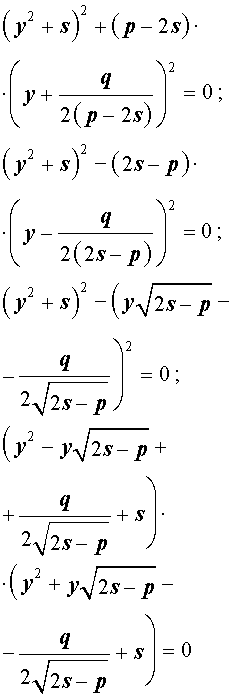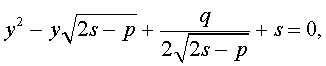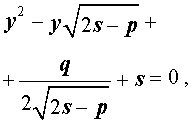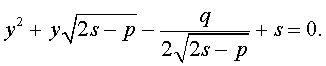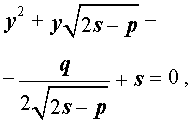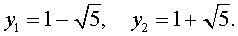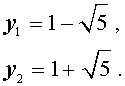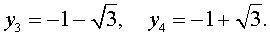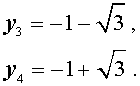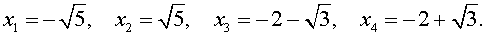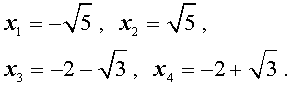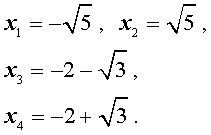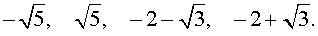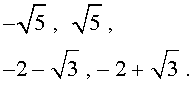Решение уравнений 4-ой степени. Метод Феррари
 Схема метода Феррари Схема метода Феррари |
 Приведение уравнений 4-ой степени Приведение уравнений 4-ой степени |
 Разложение на множители. Кубическая резольвента Разложение на множители. Кубическая резольвента |
 Пример решения уравнения 4-ой степени Пример решения уравнения 4-ой степени |
Схема метода Феррари
Целью данного раздела является изложение метода Феррари , с помощью которого можно решать уравнения четвёртой степени
| a0x 4 + a1x 3 + a2x 2 + + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем
Метод Феррари состоит из двух этапов.
На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Приведение уравнений 4-ой степени
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 4 + ax 3 + bx 2 + + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа.
Сделаем в уравнении (2) замену
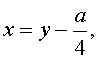 | (3) |
где y – новая переменная.
то уравнение (2) принимает вид
В результате уравнение (2) принимает вид
Если ввести обозначения
то уравнение (4) примет вид
| y 4 + py 2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа.
Первый этап метода Феррари завершён.
Разложение на множители. Кубическая резольвента
Добавив и вычитая в левой части уравнения (5) выражение
где s – некоторое число, которое мы определим чуть позже, из (5) получим
Следовательно, уравнение (5) принимает вид
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения
то уравнение (6) примет вид
Избавляясь от знаменателя, уравнение (7) можно переписать в виде
или, раскрыв скобки, — в виде
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).
Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение
а также квадратное уравнение
Вывод метода Феррари завершен.
Пример решения уравнения 4-ой степени
Пример . Решить уравнение
| x 4 + 4x 3 – 4x 2 – – 20x – 5 = 0. | (12) |
Решение . В соответствии с (3) сделаем в уравнении (12) замену
| x = y – 1. | (13) |
то в результате замены (13) уравнение (12) принимает вид
| y 4 – 10y 2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства
| p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение
которое при сокращении на 2 принимает вид:
| s 3 + 5s 2 – 8s – 42 = 0. | (16) |
| s = – 3. | (17) |
Подставляя значения (15) и (17) в формулу (10), получаем уравнение
Подставляя значения (15) и (17) в формулу (11), получаем уравнение
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):
Замечание . При решении примера мы попутно получили разложение левой части уравнения (14) на множители:
| y 4 – 10y 2 – 4y + 8 = = (y 2 – 2y – 4) (y 2 + + 2y – 2). | (20) |
Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.
Уравнение четвертой степени
Квадратные уравнения, уравнения третьей степени, уравнения четвертой степени – как это все не ново, но только жизнь такая штука, что стоит только покинуть стены родной школы, как все знания также покидают наши головы. Да и решение такого рода уравнений зачастую отнимает слишком много времени, которого в современном ритме жизни и так всегда не хватает.
Наш онлайн калькулятор поможет вам решить любое уравнение, особенно, он поможет тем, для кого ход решения не так важен как правильный ответ. Все что о вас может потребоваться это ввести искомые значения в уравнение и ровно через пару секунд вы получите значение всех неизвестных. Наш онлайн калькулятор это легко, просто и быстро!
Уравнение четвертой степени
Равенство, содержащее неизвестное число, которое обозначено буквой, называется уравнением. Решение уравнения предполагает нахождение всех значений неизвестного (неизвестных), при которых соблюдается верное равенство. Такие значения неизвестного (неизвестных) являются корнями или решением уравнения.
Уравнение вида ах 4 + bх 3 + сх 2 + dх + е = 0 называется уравнением 4-й степени с одним неизвестным. В результате решения уравнения получается 4 комплексных или вещественных корня.
Для решения приведенного уравнения 4-й степени вида: х 4 + Ах 3 + Вх 2 +Сх + D = 0 можно воспользоваться методом Феррари.
Составим кубическое уравнение: у 3 — Ву 2 + (АС — 4D)у — А 2 D + 4ВD — С 2 = 0.
Решаем полученное уравнение, находим один из его вещественных корней у0, который используем для дальнейшего нахождения корней квадратных уравнений.
Получаем и решаем два квадратных уравнения: 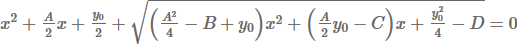
Если дано биквадратное уравнение 4-й степени вида: Ах 4 + Вх 2 + С = 0 и нужно найти его корни, можно свести его к квадратному, заменив переменную х 2 на у (у = х 2 ). В результате получим уравнение вида: Ау 2 + Ву + С = 0. Далее решаем квадратное уравнение через дискриминант.
Если дано возвратное уравнение 4-й степени вида: Ах 4 + Вх 3 + Сх 2 + Вх + А = 0 и нужно найти его корни, следует разделить уравнение на х 2 , получим:
Ах 2 + Вх + С + В / х + А / х 2 = 0.
Группируем и выносим коэффициенты за скобки: Ах 2 + А / х 2 + Вх + В / х + С = 0; А(х 2 + 1 / х 2 ) + В(х + 1 / х) + С = 0.
Произведем замену переменных: х + 1 / х = у; х 2 + 1 / х 2 = у 2 — 2, получим: А(у 2 — 2) + Ву + С = 0.
Сводим уравнение 4-й степени к квадратному уравнению и решаем его через дискриминант Ау 2 + Ву + С — 2А = 0.
Находим у1 и у2, после чего возвращаемся к замене и находим корни.
Быстро решить любое уравнение вы сможете с помощью представленного на сайте онлайн калькулятора.
http://allcalc.ru/node/552
http://infofaq.ru/uravnenie-chetvertoj-stepeni.html