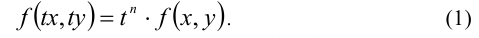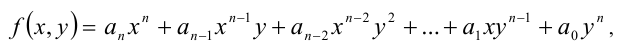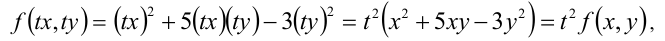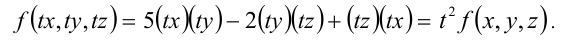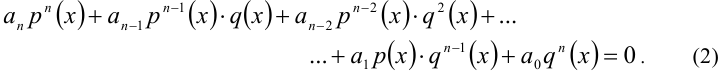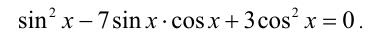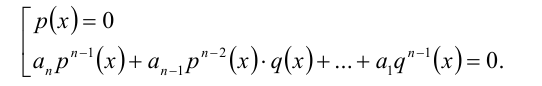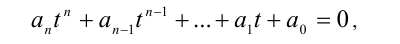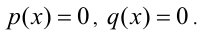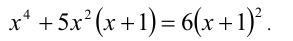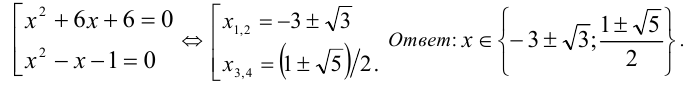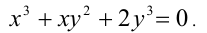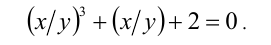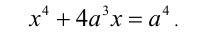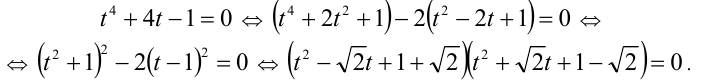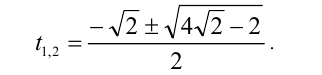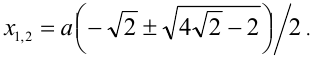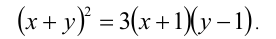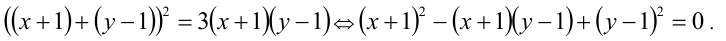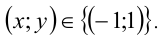Однородные уравнения и неравенства
Однородные уравнения – это уравнения, в которых все слагаемые имеют одинаковую суммарную степень.
Однородные неравенства – это неравенства, в которых все слагаемые имеют одинаковую суммарную степень.
Пример. Решить уравнение \(\sinx=\sqrt<3>\cosx\).
Ответ | Уравнение | Ответ |
x = | x = | |
x = — | x = — | |
x = — | x = | |
x = | x = 2 | |
x = | x = |
II. Изучение нового материала
A. sin x — 
Заканчивая предыдущий урок, я сказала, что пока мы не умеем решать такое уравнение, но некоторые сомневались и предлагали разделить обе части уравнения на cos x. Сохранится ли равносильность? Может быть, решения уравнения cos x = 0 являются решениями данного уравнения? Нет! Почему? Как это доказать?
Если cos x = 0 , то sin x — 

sin x — 
tg x — 




(Ответ: x = 


Если это неубедительно, то обратимся к квадратному уравнению у 2 — у = 0; если разделим его на у, то потеряем корень 0.
Можно ли делить на sin x? Если делить на sin x, то выдвигать условие sin x 

Учащиеся изучают “Материалы к уроку”.
Материалы к уроку (раздаются каждому ученику)
Тема урока: “Однородные уравнения и уравнения, сводимые к однородным”
a·sin 2 x + b·sin x·cos x + c·cos 2 x = 0,
a·sin 3 x + b·sin 2 x·cos x + c·sin x·cos 2 x + d·cos 3 x = 0 и т.д.,
где a, b, с, d — действительные числа, называют однородными относительно sin x и cos x.
2. Сумма показателей степеней при sin x и cos x у всех членов такого уравнения одинакова. Эта сумма называется степенью однородного уравнения. Рассмотренные уравнения имеют соответственно первую, вторую и третью степень.
3. Делением на cos k x, где k — степень однородного уравнения, уравнение приводится к алгебраическому относительно функции tg x.
4. Разделим обе части уравнения на cos x. Значения x, при которых cos x = 0, не являются решениями данного уравнения, т.к. если cos х = 0, то и sin x должен обращаться в 0, а косинус и синус одного аргумента не могут быть равны нулю одновременно. Следовательно, при делении на cos x получаем уравнение, равносильное данному.
5. Например, sin x — 


B. sin 2 x + sin x cos x — 2cos 2 x = 0 — однородное II степени.
sin 2 x + sin x cos x — 2cos 2 x = 0 | : cos 2 x
cos 2 x 

tg 2 x + tg x — 2 = 0
Пусть tg x = t, тогда t 2 + t — 2 = 0.
В полученном квадратном уравнении a + b + c = 0, значит, t1 = 1, t2 = — 2.
tg x = 1 или tg x = — 2
x = 




Ответ: x = 




C. sin x cos x — 3cos 2 x + 1 = 0. Является ли уравнение однородным?
Нет, т.к. слагаемое 1 — нулевой степени. Следовательно, чтобы привести это уравнение к однородному необходимо заменить 1 на sin 2 x + cos 2 x.
sin x cos x — 3cos 2 x + sin 2 x + cos 2 x = 0
sin 2 x + sin x cos x — 2 cos 2 x = 0 | : cos 2 x
tg 2 x + tg x — 2 = 0 и т.д. (см. пример B).
D. 4 sin 2 x + sin x cos x + cos 2 x = 3 — уравнение не является однородным.
4 sin 2 x + sin x cos x + cos 2 x = 3(sin 2 x + cos 2 x)
4 sin 2 x + sin x cos x + cos 2 x — 3 sin 2 x — 3 cos 2 x = 0
sin 2 x + sin x cos x — 2 cos 2 x = 0 | : cos 2 x однородное II степени
tg 2 x + tg x — 2 = 0 и т.д. (см. пример B).
E. sin 2 x + 3sin x cos x — 8cos 2 x = — 2 — уравнение не является однородным.
sin 2 x + 3sin x cos x — 8cos 2 x + 2(sin 2 x + cos 2 x) = 0
3sin 2 x + 3sin x cos x — 6cos 2 x = 0 | : 3
sin 2 x + sin x cos x — 2 cos 2 x = 0 | : cos 2 x однородное II степени
tg 2 x + tg x — 2 = 0 и т.д. (см. пример B)
III. Устная работа
Указать прием решения уравнения:
2) 3sin 2 x — 4sin x cos x + cos 2 x = 0
3) sin 3 x cos x — 2sin 2 x cos 2 x = 3sin x cos 3 x — 6cos 4 x
4) sin 2 x + sin 2x = 0 (sin 2 x + 2sin x cos x = 0)
5) cos 2 x + sin 2x = 0 (cos 2 x + 2sin x cos x = 0)
IV. Неполные однородные уравнения
Уравнения 4) и 5) из устной работы два ученика решают одновременно на доске.
Традиционная ошибка школьников при решении неполных однородных уравнений II степени делением на одну из функций — потеря корней. Решая уравнения разложением на множители оба ученика получают две серии корней. А при решении новым способом (деление на функцию) у одного получаются две серии корней, а у другого — одна. В чём ошибка?
После обсуждения проблемы сформулировали вывод: “дели на то, чего мало”.
sin 2 x + 2sin x cos x = 0.
разложим левую часть уравнения на множители
sin x = 0 или sin x + 2cos x = 0 | : cos x (получили однородное уравнение I степени)
x = 



Ответ: x = 



Решаем данное уравнение как однородное II степени
sin 2 x + 2sin x cos x = 0 | : cos 2 x
tg 2 x + 2tg x = 0
tg x = 0 или tg x + 2 = 0
x = 



cos 2 x + 2sin x cos x = 0.
I способ (решаем как однородное уравнение II степени):
cos 2 x + 2sin x cos x = 0 | : sin 2 x (“дели на то, чего мало”)
если sin x = 0, то cos 2 x + 2·0·cos x = 0 U сos x = 0,что невозможно
сtg 2 x + 2сtg x = 0
сtg x = 0 или сtg x + 2 = 0
х = 





Ответ: х = 





II способ для проверки (решаем разложением на множители):
cos x (cos x + 2sin x ) = 0
cos x = 0 или cos x + 2sin x = 0 | : cos x
х = 



x = — arctg 


V. Самостоятельная работа
1)
1)
2)
2)
3)
 sin 2x — 5cos 2 x = 2
sin 2x — 5cos 2 x = 23)
 sin 2x — cos 2 x = 2
sin 2x — cos 2 x = 24)
 + x) + 3 cos 2 (
+ x) + 3 cos 2 (  + x) =1
+ x) =14)
 —
—  sin x + 5sin 2
sin x + 5sin 2  = 3
= 35)
5)
Ответы: во всех случаях полагается n, kI Z
1)
 +
+  n.
n.1)
 +
+  n.
n.2)
 +
+  n; x = arctg
n; x = arctg  +
+  k.
k.2)
 +
+  n; x = arctg 3 +
n; x = arctg 3 +  k.
k.3)
 +
+  n; x = — arctg
n; x = — arctg  +
+  k.
k.3)
 +
+  n; x = arctg
n; x = arctg  +
+  k.
k.4)
 +
+  n.
n.4)
 + 2
+ 2 n; x = 2arctg
n; x = 2arctg  + 2
+ 2 k.
k.5)
 + 2
+ 2 n; x = 2arctg
n; x = 2arctg  + 2
+ 2 k.
k.5)

VI. Домашнее задание (Колмогоров А.Н. и др., “Алгебра и начала анализа”)
VII. Рефлексия (ответы на вопросы ученики пишут на листочках и сдают их учителю)
Однородные уравнения
Однородные уравнения
Алгебраический многочлен f(x,y) с двумя переменными x и у называется однородным многочленом n -й степени относительно этих переменных 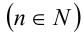
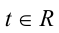
Это означает, что однородный многочлен n-й степени f (х, у) можно представить в виде
где 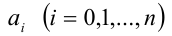
Уравнение f(x,y) = 0 называется однородным алгебраическим уравнением n -й степени с двумя неизвестными x,у, если f(x,y) — однородный многочлен n-й степени относительно этих переменных.
Например, уравнение вида 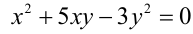
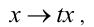
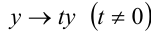
т.е. условие (1) из определения выполняется (n = 2).
Аналогично, уравнение 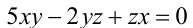
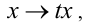
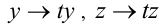
Итак, однородное алгебраическое уравнение — это уравнение, не меняющее своего вида при одновременном умножении всех его неизвестных на одно и то же число, отличное от нуля. Можно распространить понятие однородности на случай неалгебраических уравнений.
Пусть р(х) и q(x) — две произвольные функции, определённые на одном и том же множестве, 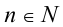
Однородным уравнением n -й степени относительно функций р(х), q(x) называется уравнение вида
В частности, если функции р(х) и q(x) являются целыми алгебраическими многочленами, то и уравнение (2) будет относиться к аналогичному классу. В качестве другого примера рассмотрим уравнение вида
Оно является однородным тригонометрическим уравнением 2-й степени относительно функций
Перейдём к процедуре решения уравнения (2).
Если хотя бы один из коэффициентов 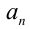
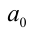
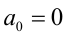
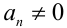
Если же 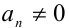
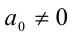
1) Если 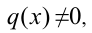
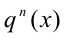
решив которое и сделав обратную подстановку, найдём часть решений однородного уравнения.
2) Если q(х) = 0. то, подставив в уравнение вместо q(x) нуль, получим, что тогда и р(х) должно обращаться в нуль. Таким образом, этот случай сводится к решению системы уравнений
Осталось объединить все найденные решения. Уравнение (2) решено. Обратимся к примерам.
Пример №185.
Решить уравнение
Решение:
Перепишем уравнение: 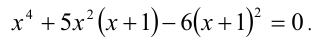
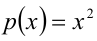
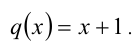
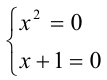
2) Пусть теперь 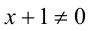
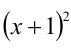
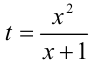
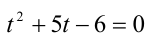
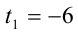
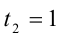
Пример №186.
Решить в целых числах уравнение
Решение:
Заметим, что если у = 0, то x = 0, и, значит, пара (0;0) удовлетворяет уравнению. Пусть 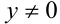
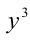
Обозначим t = x/у, тогда имеем кубическое уравнение 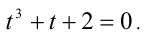
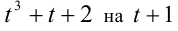
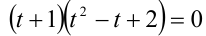
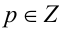
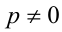
Ответ: 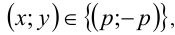
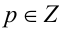
Пример №187.
Для каждого действительного значения параметра а решить уравнение
Решение:
Заметим, что данное уравнение можно рассмотреть как однородное алгебраическое уравнение 4-й степени относительно x и а.
1) Если а = 0 , то х = 0 .
2) Если 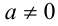
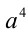
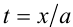
Первый сомножитель в нуль не обращается, а второй имеет два корня
Ответ: при а = 0 единственное решение x = 0 ;
при 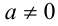
Пример №188.
Найти действительные корни уравнения
Решение:
Данное уравнение в исходном виде не является однородным, но может быть сведено преобразованиями к однородному. Действительно, достаточно привести его к виду
Получили однородное уравнение 2-й степени относительно x + 1 и у — 1.
1) Если 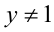
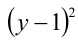
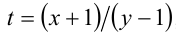
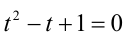
2) Если у = 1, то, подставляя в уравнение, находим x = — 1 .
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://urok.1sept.ru/articles/212251
http://lfirmal.com/odnorodnyie-uravneniya-v-matematike/

 +
+ 
 +
+  +
+ 
 +
+