Решить показательное уравнение и неравенство калькулятор

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение показательных неравенств.

Этот математический калькулятор онлайн поможет вам решить показательное неравенство. Программа для решения показательного неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное неравенство
Решить неравенство

Немного теории.

Показательные неравенства

Неравенства вида
\( a^x > b \) и \( a^x 0, \; a \neq 0, \; b \in \mathbb \)
называют простейшими показательными неравенствами.

Напомним, что решением неравенства называют число \(x_0\), при подстановке которого в неравенство получается верное числовое неравенство.

Решить неравенство — значит найти все его решения или показать, что их нет.

Случай \( b \leqslant 0\)

Поскольку \( a^x >0 \) для любого \( x \in \mathbb \), то при \( b \leqslant 0\) неравенство \( a^x > b \) верно для любого \( x \in \mathbb \).
И нет ни одного \( x \in \mathbb \) для которого было бы верно неравенство \( a^x \leqslant b \) при \( b \leqslant 0\).

Таким образом, если \( b \leqslant 0\), то множество всех решений неравенства \( a^x > b \) есть интервал \( (-\infty; \; +\infty) \), а неравенство \( a^x 0\)

Если же \( b > 0\), то исходные неравенства можно переписать в виде
\( a^x > a^c \) и \( a^x 1\)

Рассмотрим решение неравенств \( a^x > a^c \) и \( a^x 1\)
Так как для такого \(a\) функция \( y = a^x \) является возрастающей, то для любого числа \( x > c \) верно неравенство \( a^x > a^c \), а для любого числа \( x 0\) и \( a > 1\) множество всех решений неравенства \( a^x > a^c \) есть интервал \( (c; \; +\infty) \), а множество всех решений неравенства \( a^x c \) верно неравенство \( a^x a^c \).
Кроме того, равенство \( a^x = a^c \) справедливо лишь при \( x = c \).

Таким образом, при \( b > 0\) и \( 0 a^c \) есть интервал \( (-\infty; \; c) \), а множество всех решений неравенства \( a^x 0, то неравенство можно переписать в виде \(2x 1, то функция \(y = 2^x\) возрастающая. Поэтому решением неравенства, являются все x 0, то это неравенство можно переписать в виде
$$ \left( \frac<1><3>\right)^x log_<\frac<1><3>>5 \)
Ответ: \( (log_<\frac<1><3>>5 ; \; +\infty) \)

ПРИМЕР 3. Решим неравенство \( 2^ + 2^

Решить показательное уравнение и неравенство калькулятор

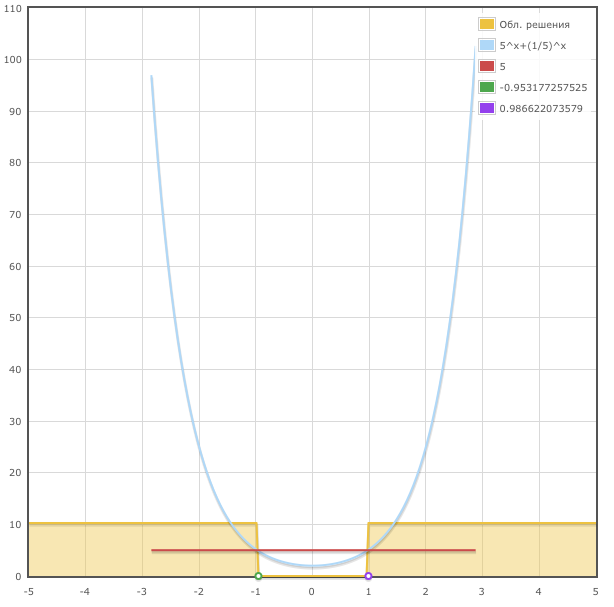
>>решение неравенств онлайн 5$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$5^ + \left(\frac<1><5>\right)^ = 5$$ Решаем:
Дано уравнение: $$5^ + \left(\frac<1><5>\right)^ = 5$$ или $$5^ + \left(\frac<1><5>\right)^ — 5 = 0$$ Сделаем замену $$v = \left(\frac<1><5>\right)^$$ получим $$v — 5 + \frac<1> = 0$$ или $$v — 5 + \frac<1> = 0$$ делаем обратную замену $$\left(\frac<1><5>\right)^ = v$$ или $$x = — \frac<\log<\left (v \right )>><\log<\left (5 \right )>>$$ $$x_ <1>= \frac<1><\log<\left (5 \right )>> \left(- \log <\left (2 \right )>+ \log <\left (\sqrt<21>+ 5 \right )>\right)$$ $$x_ <2>= \frac<1><\log<\left (5 \right )>> \left(\log <\left (- \sqrt<21>+ 5 \right )> — \log<\left (2 \right )>\right)$$ $$x_ <1>= \frac<1><\log<\left (5 \right )>> \left(- \log <\left (2 \right )>+ \log <\left (\sqrt<21>+ 5 \right )>\right)$$ $$x_ <2>= \frac<1><\log<\left (5 \right )>> \left(\log <\left (- \sqrt<21>+ 5 \right )> — \log<\left (2 \right )>\right)$$ Данные корни $$x_ <2>= \frac<1><\log<\left (5 \right )>> \left(\log <\left (- \sqrt<21>+ 5 \right )> — \log<\left (2 \right )>\right)$$ $$x_ <1>= \frac<1><\log<\left (5 \right )>> \left(- \log <\left (2 \right )>+ \log <\left (\sqrt<21>+ 5 \right )>\right)$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_ <0>5$$

значит одно из решений нашего неравенства будет при:
$$x \frac<1><\log<\left (5 \right )>> \left(- \log <\left (2 \right )>+ \log <\left (\sqrt<21>+ 5 \right )>\right)$$

Также вы будете иметь графическое решение показательного неравенства:

Тэги: неравенство

© Контрольная работа РУ — примеры решения задач

Решение показательных уравнений онлайн

Показательным называется уравнение в котором неизвестная переменная находится в степени, например:

Для решения таких уравнений применяются различные подходы, одним из которых является логарифмирование. Например, прологарифмируем обе части, приведенного выше уравнения:

Приведенный выше пример является простейшим. Наш калькулятор, построенный на системе Wolfram Alpha способен решить практически любые показательные уравнения с подробным решением.