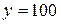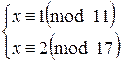Решить систему уравнений используя китайскую теорему об остатках

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Вспомогательная страница к разделу МОДУЛЯРНАЯ АРИФМЕТИКА

Китайская теорема об остатках

Пример [1]. Найти натуральное число, которое при делении на $ 3_<> $ дает в остатке $ 2_<> $, при делении на $ 7_<> $ дает в остатке $ 3_<> $, а при делении на $ 10_<> $ — в остатке $ 9_<> $.

Решение. Пусть $ u,v,w $ — частные от деления неизвестного числа на $ 3, 7 $ и $ 10_<> $ соответственно. Имеем: $$ 3\,u+2=7\,v+3,\ 3\,u+2=10\, w+9,\ 7\,v+3=10\, w+9 \ . $$ Решаем последнее уравнение в целых числах, применяя рассуждения, приведенные ☞ ЗДЕСЬ: $$ w=7\,t_1-2,\ v=10\,t_1-2 \quad npu \quad \forall t_1 \in \mathbb Z \ . $$ Подставим найденное выражение для $ v_<> $ в первое уравнение $ 3\,u+2=7\,v+3 $: $$ 3\,u-70\, t_1=-13 \ , $$ которое также можно решить: $ u=19+70\, t_2 $ при $ \forall t_2 \in \mathbb Z $. Следовательно, общий вид искомых чисел: $$ 3\,u+2=3 (19+70\, t_2)+2=59+210\, t_2 \quad npu \quad \forall t_2 \in \mathbb Z \ . $$ Наименьшее положительное число получается при $ t_2=0 $.

Ответ. $ 59 $.

Теорема [Китайская теорема об остатках (КТО)]. Пусть числа $ M_1 , M_2, \dots, M_k $ — попарно взаимно простые, и $$ M= M_1 M_2 \times \dots \times M_k \ .$$ Тогда система

$$ x \equiv B_1 \pmod,\ x \equiv B_2 \pmod, \dots,\ x \equiv B_k \pmod $$ имеет единственное решение среди чисел $ \ <0,1,\dots,M-1 \>$, и это решение может быть представлено в одном из следующих видов:
1. либо $ x = x_1 \pmod $ при $$ x_1= \frac B_1 y_1 +\frac B_2 y_2+ \dots + \frac B_k y_k $$ и $ y_j $ обозначающем число, обратное числу $ M\big/ M_j $ относительно умножения по модулю $ M_j $: $$\frac y_j \equiv 1 \pmod \ ;$$ 2. либо $ x = x_2 \pmod $ при $$ x_2= B_1 +z_1M_1+z_2M_1M_2 +\dots + z_M_1M_2\times \dots \times M_ \ , $$ и числах $ z_1,\dots,z_ $ последовательно определяемых из сравнений $$ \begin B_1+z_1M_1 &\equiv B_2 \pmod \, , & \\ B_1 +z_1M_1+z_2M_1M_2 &\equiv B_3 \pmod \, ,& \\ \dots & \dots & \\ B_1 +z_1M_1+z_2M_1M_2 +\dots + z_M_1M_2\times \dots \times M_ & \equiv B_k \pmod \, . & \end $$

Доказательство. 1. При любых целых числах $ y_2,\dots,y_k $ число $ x_ <1>$, определяемое формулой 1 , удовлетворяет сравнению $$x_1\equiv \frac B_1 y_1 \pmod$$ (поскольку числа $ M/M_2,\dots,M/M_k $ делятся на $ M_ <1>$). Пусть число $ y_1\in \ < 1, \dots ,M_1-1 \>$ удовлетворяет сравнению $$\frac y_1 \equiv 1 \pmod$$ (на основании теоремы существования и предположений доказываемой теоремы такое число существует и оно единственно). Тогда $ x_1\equiv B_1 \pmod $, т.е. удовлетворяет первому из сравнений системы. Аналогично показывается справедливость остальных сравнений.

2. Фактически, этот алгоритм заключается в последовательном решении сравнений системы. Решение первого имеет вид $ B_1+M_1t_1 $ при $ t_1\in \mathbb Z $; оно подставляется во второе, из которого находим представление для $ t_1 $ в виде $ t_1=z_1+M_2t_2 $ при $ t_2\in \mathbb Z $, и т.д. Формально: число $ x_2 $, определяемое формулой 2 , очевидно удовлетворяет первому из сравнений системы: $ x_2 \equiv B_1 \pmod $. Далее, $ x_2\equiv B_1+ z_1M_1 \pmod $ и сравнение $ x_2 \equiv B_2 \pmod $ будет выполнено, если $ z_1 $ удовлетворяет сравнению $ B_1+ z_1M_1 \equiv B_2 \pmod $. Поскольку $ \operatorname (M_1,M_2)=1 $, то на основании теоремы существования, такое число существует и оно единственно при условии $ z_1\in \ < 1, \dots ,M_2-1 \>$. Установив его, продолжаем далее по индукции.

В заключение покажем, что любые два решения $ \tilde $ и $ \tilde<\tilde> $ системы сравнимы между собой по модулю $ M_<> $. В самом деле: $$ \tilde \equiv B_j \pmod,\ \tilde<\tilde> \equiv B_j \pmod \ \Rightarrow \ \tilde — \tilde<\tilde> \equiv 0 \pmod $$ для $ \forall j \in \ <1,\dots, k \>$. Поскольку числа $ M_1,\dots,M_ $ попарно взаимно просты, то на основании теоремы 4, приведенной ☞ ЗДЕСЬ, имеем: $ \tilde — \tilde<\tilde> \equiv 0 \pmod $. ♦

Математическое руководство Сунь Цзы

китайского математика Сунь Цзы 1) (孫子, ок. 400 — ок. 460), о котором не известно ничего, кроме того, что он является автором этой книги; годы его жизни устанавливались историками науки на основе анализа текста.

Задача 26 главы 3. Предположим, что имеется неизвестное количество объектов. Разбив их на тройки, получаем в остатке 2, разбив на пятерки — 3, разбив на семерки — 2. Сколько имеется объектов?

После решения этой конкретной задачи, в книге приводится алгоритм решения и общей — при произвольных остатках:

«Умножь число остатков при делении на тройки на $ 70 $, добавь к полученному произведение числа остатков при делении на пятерки на $ 21 $, и затем добавь произведение числа остатков при делении на семерки на $ 15 $. Если результат равен $ 106 $ или более — вычти кратное $ 105 $.»

Эти рассуждения фактически соответствуют представлению решения системы формулой 2 .

Некоторые специалисты полагают, что алгоритм решения системы сравнений позволял китайским генералам пересчитывать армию без особых усилий последовательностью однотипных распоряжений:

«В колонну по $ 7_<> $ становись!»

По выполнении команды, подсчитывалось количество солдат, стоящих в последнем ряду. Затем производились аналогичные подсчеты по результатам выполнения команд:

«В колонну по $ 11 $ становись!»

«В колонну по $ 13 $ становись!»

«В колонну по $ 17 $ становись!»

В соответствии с утверждением теоремы, по четырем остаткам однозначно восстанавливается число солдат, если оно не превосходит $ 17017=7\times 11\times 13 \times 17 $.

Однако некоторые соображения, основанные на знании реалий армейской жизни, позволяют усомниться в практической пользе подобных — математически абсолютно безупречных — рассчетов… — см. упражнение ниже.

Пример 1. Решить систему сравнений

$$x \equiv 7 \pmod<8>,\ x \equiv -1 \pmod<11>,\ x \equiv 3 \pmod <15>\ .$$

Решение. Проиллюстрируем оба способа из теоремы. Для представления 1 сначала решаем сравнения $$165 \cdot y_1 \equiv 1 \pmod <8>,\quad 120 \cdot y_2 \equiv 1 \pmod <11>,\quad 88 \cdot y_3 \equiv 1 \pmod <15>\ , $$ которые, очевидно, эквивалентны следующим: $$ 5 \cdot y_1 \equiv 1 \pmod <8>,\quad 10 \cdot y_2 \equiv 1 \pmod <11>,\quad 13 \cdot y_3 \equiv 1 \pmod <15>\ . $$ Алгоритм решения линейного сравнения даст решения в виде $$y_1=5, \quad y_2=10 , \quad y_3=7 \ . $$ По формуле 1 получаем $$x_1= \underbrace<7\cdot 5 \cdot 165 + (-1)\cdot 10 \cdot 120 + 3 \cdot 7 \cdot 88>_ <6423>= 1143+1320\times 4 \equiv 1143 \pmod <1320>\ .$$

Для 2 решением сравнения $ 7+ 8\, z_1 \equiv -1 \pmod <11>$ очевидно является $ z_1 \equiv_<_<11>> -1 \equiv_<_<11>> 10 $. Сравнение $ 7+8 \cdot 10 + 8\cdot 11 \, z_2 \equiv 3 \pmod <15>$ эквивалентно $ 13\, z_2 \equiv 6 \pmod <15>$ и имеет решение $ z_2=12 $. Окончательно $$x_2= 87 + 8\cdot 11 \cdot 12 =1143 \ .$$

Ответ. $ x \equiv 1143 \pmod <1320>$.

При вычислениях по формуле 1 один из коэффициентов $ y_jM/ $ можно легко установить, если все остальные уже вычислены:

Доказать, что при условиях (и в обозначениях) теоремы имеет место сравнение

$$ \frac y_1 +\frac y_2+ \dots + \frac y_k \equiv 1 \pmod \ . $$

Какой из алгоритмов теоремы — 1 или 2 — предпочтителен при расчетах ?

Для фиксированной системе сравнений эти алгоритмы равноэффективны. Однако если идет речь о решении серии однотипных систем с изменением входящих в них параметров, то проявляются преимущества каждого из алгоритмов. Рассмотрим сначала серию систем сравнений $$ x \equiv B_1 \pmod,\ x \equiv B_2 \pmod, \dots,\ x \equiv B_k \pmod $$ при фиксированном их числе $ k_<> $ и фиксированных же модулях $ M_1,\dots,M_ $, но варьируемых $ B_1,\dots,B_ $. В этом случае имеет смысл использовать представление решения в форме 1 , поскольку для получения решения каждой новой системы серии нужно будет произвести лишь пересчет суммы при уже вычисленных ранее величинах $ y_1,\dots,y_k $. С другой стороны, если решается серия систем сравнений, в которой каждая следующая система получается из предыдущей добавлением одного нового сравнения — т.е., например, система дополняется сравнением $ x\equiv B_ \pmod> $ — то более удобным для вычисления решения становится вариант 2 , так как при его использовании приходится дополнительно решать лишь одно новое сравнение относительно $ z_ $ и добавить соответствующее слагаемое в сумму — т.е. просто прибавить его к решению стартовой системы.

Пример 2. Решить системы сравнений

а) $ x \equiv 3 \pmod<8>,\ x \equiv 1 \pmod<11>,\ x \equiv 12 \pmod <15>$;

б) $ x \equiv 7 \pmod<8>,\ x \equiv -1 \pmod<11>,\ x \equiv 3 \pmod<15>,\ x \equiv 4 \pmod <7>$.

Решение. Обе системы могут рассматриваться как вариации одной и той же системы примера 1, и решение каждой из этих систем может быть получено модифицированием соответствующего варианта решения того примера. Так, для системы а) получить решение не представляет труда, если были заранее вычислены величины $ y_1,y_2 $ и $ y_3 $: $$x_1= \underbrace<3\cdot 5 \cdot 165 + 1\cdot 10 \cdot 120 + 12 \cdot 7 \cdot 88>_ <11\,067>\equiv 507 \pmod <1320>\ .$$ А для системы б) удобнее использовать алгоритм 2 теоремы, тем более, что решение системы из первых трех сравнений у нас уже имеется. $$ 1320\, z_4 \equiv 4 \pmod <7>\quad \Rightarrow \quad z_4 =4 \quad \Rightarrow \quad x_2 =1143+1320\, z_4 =6423 \ . $$

Ответ. а) $ x \equiv 507 \pmod <1320>$; б) $ x \equiv 6423 \pmod <9240>$.

Определить число $ x_<> $ солдат китайской армии, если

а) $ x \equiv 3 \pmod<7>,\ x \equiv 1 \pmod<11>, \ x \equiv 12 \pmod<13>,\ x \equiv 10 \pmod <17>$;

б) $ x \equiv 3 \pmod<7>,\ x \equiv 1 \pmod<11>, \ x \equiv 12 \pmod<13>,\ x \equiv 11 \pmod <17>$.

Доказать, что если $ p_1,p_2,p_3 $ — различные простые числа, то а) решение системы

$$ x \equiv B_1 \pmod,\ x \equiv B_2 \pmod, \ $$ можно представить в виде $$ x \equiv p_2^B_1 + p_1^B_2 \pmod \ , $$ а б) решение системы $$ x \equiv B_1 \pmod,\ x \equiv B_2 \pmod, \ x \equiv B_3 \pmod $$ — в виде $$ x \equiv p_2^p_3^ B_1 + p_1^ p_3^ B_2 + p_1^p_2^ B_3 \pmod \ . $$ Решить эти системы при $ B_1=1,B_2=2,B_3=3 $ и $ p_1=7,p_2=11,p_3=17 $.

Cистема сравнений может иметь решения и при нарушении условий КТО.

[Фибоначчи]. Крестьянка несла на базар корзину яиц. Неосторожный всадник, обгоняя женщину, задел корзину, и все яйца разбились. Желая возместить ущерб, всадник спросил у крестьянки, сколько яиц было в корзине. Женщина ответила, что числа яиц не знает, но когда она раскладывала их по два, по три, по четыре, по пять и по шесть, то каждый раз одно яйцо оставалось лишним, а когда она разложила по семь, лишних яиц не осталось. Сколько яиц несла крестьянка на базар?

Теорема. Система

$$ x \equiv B_1 \pmod,\ x \equiv B_2 \pmod, \dots,\ x \equiv B_k \pmod $$ разрешима тогда и только тогда, когда числа $$ B_j-B_ <\ell>\qquad \mbox < делятся на >\qquad \operatorname(M_j,M_<\ell>) \quad \mbox < при >\quad \\> \subset \ <1,\dots,k\>\quad . $$ Если это условие выполнено, то решение единственно по модулю $ \operatorname(M_1,M_2,\dots,M_k) $.

По поводу КТО см. оригинальный результат ☞ ЗДЕСЬ.

Решить систему сравнений

$$ x \equiv M_1-1 \pmod,\ x \equiv M_2-1 \pmod, \dots,\ x \equiv M_k-1 \pmod \ . $$

Интерполяция

Читатель, знакомый с проблемой интерполяции, безусловно заметит аналогию вариантов 1 и 2 китайской теоремы об остатках с формами соответственно Лагранжа и Ньютона представления интерполяционного полинома $ y_<>=f(x) $, составляемого по таблице значений $$ \begin x & M_1 & \dots & M_k \\ \hline f(x) & B_1 & \dots & B_k \end $$ Действительно, задачу интерполяции можно «перевести на язык остатков»: найти полином $ f(x)_<> $, дающий при делении на $ x-M_1 $ в остатке число $ B_ <1>$, при делении на $ x-M_2 $ в остатке $ B_ <2>$ и т.д.

Применения

Целочисленный определитель

Пример. Верно ли равенство $$ \left| \begin 51239 & 79922 & 55538 & 29177 \\ 46152 & 16596 & 37189 & 82561 \\ 71489 & 23165 & 26563 & 61372 \\ 44350 & 42391 & 91185 & 64809 \end \right|=0 \ ? $$

Решение. Фактическое вычисление подобного определителя — каким бы методом мы не воспользовались — задача довольно трудоемкая. Однако вопрос ставится не о фактическом значении, а о равенстве его нулю. Это обстоятельство может упростить вычисления. Обозначим неизвестное значение определителя через $ x_<> $; очевидно это число целое. Если $ x=0_<> $, то и его остаток при делении на любое число $ M\in \mathbb Z $ тоже должен быть равным нулю. Если же хоть для одного $ M\in \mathbb Z $ выполнится условие $ x\not\equiv 0 \pmod M $, то и $ x\ne 0 $. Вычисление определителя фактически сводится к умножению элементов определителя. Если же мы ставим задачу определения остатка от деления этого выражения на $ M_<> $, то имеет смысл сразу же «сократить» каждый элемент определителя до его остатка от деления на $ M_<> $.

Возьмем сначала $ M=10 $, т.е. от каждого элемента определителя оставляем только последнюю цифру: $$ \left| \begin 9 & 2 & 8 & 7 \\ 2 & 6 & 9 & 1 \\ 9 & 5 & 3 & 2 \\ 0 & 1 & 5 & 9 \end \right| \equiv_<_<10>> \left| \begin -1 & 2 & -2 & -3 \\ 2 & -4 & -1 & 1 \\ -1 & 5 & 3 & 2 \\ 0 & 1 & 5 & -1 \end \right| = \left| \begin -1 & 2 & -2 & -3 \\ 0 & 0 & -5 & -5 \\ 0 & 3 & 5 & -5 \\ 0 & 1 & 5 & -1 \end \right|= $$ $$ =- \left| \begin 0 & -5 & -5 \\ 3 & 5 & -5 \\ 1 & 5 & -1 \end \right| \equiv_<_<10>> 0 \ . $$ Итак, полученный ответ является необходимым, но не достаточным условием равенства определителя нулю. Сделаем еще одну проверку: возьмем $ M=7 $. $$ \left| \begin 6 & 3 & 0 & 1 \\ 1 & 6 & 5 & 3 \\ 5 & 2 & 5 & 3 \\ 5 & 6 & 3 & 3 \end \right|\equiv_<_<7>> 3 \ne 0 \ . $$

Ответ. Равенство неверно.

Понятно, что если бы определитель был равен нулю, то каждое вычисление по модулю только «увеличивало бы достоверность» этого события.

Можно ли на основе серии модулярных вычислений установить истинное значение определителя?

Попробуем это сделать для определителя из примера. Прежде всего, оценим сверху абсолютную величину определителя. Каждое слагаемое в разложении определителя по формуле из его определения представляет собой произведение четырех пятизначных чисел; очевидно, это произведение не превосходит $ 10^ <24>$. Всего таких слагаемых $ 24_<> $, из них половина — с отрицательным знаком. Поэтому $ |x| 2) $ p_j $, так чтобы их произведение превысило эту оценку: $$L = \underbrace<2\cdot 3 \cdot 5 \times \dots \times 67 \cdot 71>_ <20>> 1.2\cdot 10^ <25>$$ и вычисляем остатки $ B_= x \pmod $: $$B_2=0, B_3=0, B_5=0, B_7=3, B_<11>=7,\dots, B_<67>=64, B_<71>=39 \ .$$ Китайская теорема об остатках позволяет однозначно определить величину $ x_<> $ если она находится в пределах $ 0 ☞ ЗДЕСЬ.

Остатки от деления числа $ x_<> $ на последовательность целых чисел

$$ x \equiv 1 \pmod<7>,\ x \equiv 4 \pmod<8>,\ x \equiv 4 \pmod<9>, $$ $$ \ x \equiv 2 \pmod<10>,\ x \equiv 2 \pmod<11>,\ x \equiv 5 \pmod <13>$$ вычислены с ошибками; известно, однако, что не более двух остатков ложные. Установите число $ x_<> $.

Остатки степенных выражений

Материал настоящего пункта является естественным продолжением соответствующего пункта из раздела МОДУЛЯРНАЯ АРИФМЕТИКА.

Пример. Вычислить $ 888888^ <777777>\pmod <1488659>$.

Решение. Вычисление «в лоб» по алгоритму квадрирования-умножения кажется чудовищным; упрощение, предложенное в ☞ ПУНКТЕ, в данном конкретном случае не сработает: $ 777777 ☞ ЗДЕСЬ.

Приведенные в предыдущих пунктах примеры позволяют сформулировать основной принцип практического использования КТО: элементарные операции с большими числами подменяются аналогичными операциями над их остатками при делении на небольшие числа $ M_j $. Можно образно сказать, что мы действуем с «проекциями» чисел на множества остатков $ \ <0,1,\dots,M_j-1\>$.

Вычислить $ 456789^ <-1>\pmod <1488659>$ .

ЗАДАЧИ

Источники

[1]. Малининъ А., Буренинъ К. Руководство алгебры и собранiе алгебраическихъ задачъ для гимназiй, реальныхъ училищъ и учительскихъ институтовъ. Изданiе седьмое. М. Издание книжнаго магазина наследников бр. Салаевыхъ. 1884.

[2]. Бухштаб А.А. Теория чисел. М. Просвещение. 1966

[3]. LeVeque W.J. Topics in Number Theory. V.1. Addison-Wesley. Mass. 1956.

[4]. Утешев А.Ю., Калинина Е.А. Лекции по высшей алгебре. Часть I. Учеб. пособие. СПб. «СОЛО». 2007. 246 c.

Применения китайской теоремы об остатках.

Китайская теорема об остатках находит широкое применение в теории чисел и криптографии.

Применение Китайской теоремы об остатках в криптосистеме RSA.

В криптосистеме RSA при расшифровании требуется вычислить y d mod n, причем известно, что n=p∙q, где p, q – большие простые числа. Как было показано ранее, степень d, в которую требуется возвести шифрованный текст, можно понизить за счет использования теоремы Эйлера. Зная разложение числа n на простые сомножители и используя китайскую теорему об остатках, возможно еще более ускорить вычисления.

Как читатель мог заметить, при вычислениях для ускорения возведения в степень используется теорема Ферма.

Получим систему сравнений

.

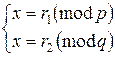
Решая ее по китайской теореме об остатках, получим решение .

Сложность возведения в степень с использованием китайской теоремы об остатках и теоремы Ферма составляет около 6k 3 против 24k 3 при использовании только теоремы Ферма (где k есть размерность числа n).

Пусть в RSA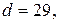

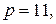
Требуется вычислить x=100 29 mod 187.

r₁=(100 mod 11) 29 mod 10 mod 11=1 9 mod 11 = 1,

r₂=(100 mod 17) 29 mod 16 mod 17=15 13 mod 17=2.

Пользуясь Китайской теоремой об остатках, решаем эту систему.

Ответ: 100 29 mod 187=155.

Схема разделения секрета на основе Китайской теоремы об остатках.

На основе китайской теоремы об остатках можно построить (n,k)–пороговую схему разделения секрета. Напомним основные принципы схем разделения секрета.

Пусть существует некая информация, которую следует сохранить в секрете, и имеется n участников, не доверяющих друг другу. Эти участники хотят, чтобы секретную информацию можно было получить только при условии того, что как минимум k участников из n собрались вместе.

(n,k)-пороговая схема разделения секрета – это схема разделения секретной информации между n участниками таким образом, чтобы только k из них (или более), собравшись вместе, могли получить этот секрет. Причем вероятность угадать верное значение секрета при наличии k–m долей секрета 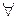m>0 равна вероятности угадать верное значение секрета без обладания долей секрета. При этом все участники протокола равноправны.

Как правило, схемы разделения секрета состоят из 2-х фаз: фазы разделения, когда каждому участнику протокола выдается его доля секрета, и фаза восстановления, когда k или более любых участников, собрав свои доли, восстанавливают общий секрет.

Схема разделения секрета на основе китайской теоремы об остатках выглядит следующим образом:

Пусть N – общий секрет.

Часть секрета, выдаваемая i-му участнику схемы, есть число x_i, вычисляемое как x_i≡N(mod p_i).

Заметим, что числа p₁, p₂,…, p_n должны быть такими, чтобы произведение любых k из них было больше, чем N. А это достигается, когда для всех i выполняется p_i> .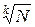

Для того, чтобы k–1 участников не смогли восстановить секрет без k-го участника, необходимо, чтобы p_i

Курсовая работа по дисциплине «Алгебра» на тему: «Китайская Теорема об остатках и её следствия»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

по дисциплине «Алгебра»

на тему: «Китайская Теорема об остатках и её следствия»

Глава 1. Элементарная теория сравнений, а ≡ b ( mod p )

. Определения и основные свойства сравнений

. Теорема Эйлера, теорема Ферма

Глава 2. Китайская теорема об остатках

. Китайская теорема об остатках (КТО)

. Примеры. Применение к решению олимпиадных задач

. КТО. Применение к открытию сейфа в банке

Первоначальные элементы математики связаны с появлением навыков счета, возникающих в примитивной форме на сравнительно ранних ступенях развития человеческого общества в процессе трудовой деятельности. Понятие натурального числа, появляющееся как результат постепенного абстрагирования, является основой всего дальнейшего развития математики. В теории чисел, естественно, выделяются и рассматриваются в первую очередь те проблемы, которые глубоко и достаточно непосредственно связаны с изучаемыми объектами и важны для построения математики в ее целом. Некоторые теоретико-числовые задачи возникают уже в рамках школьного курса арифметики. Исторически теория чисел возникла как непосредственное развитие арифметики. В настоящее время в теорию чисел включают значительно более широкий круг вопросов, выходящих за рамки изучения натуральных чисел. В теории чисел рассматриваются не только натуральные числа, но и множество всех целых чисел, а также множество рациональных чисел.

Современную теорию чисел можно в основном разбить на следующие разделы:

) Элементарная теория чисел (теория сравнений, теория форм, неопределенные уравнения). К этому разделу относят вопросы теории чисел, являющиеся непосредственным развитием теории делимости, и вопросы о представимости чисел в определенной форме. Более общей является задача решения систем неопределенных уравнений, т. е. уравнений, в которых значения неизвестных должны быть обязательно целыми числами. Неопределенные уравнения называют также диофантовыми уравнениями, так как Диофант был первым математиком, систематически рассматривавшим такие уравнения. Мы условно называем этот раздел „Элементарная теория чисел», поскольку здесь часто применяются обычные арифметические и алгебраические методы исследования.

) Алгебраическая теория чисел. К этому разделу относят вопросы, связанные с изучением различных классов алгебраических чисел.

) Диофантовы приближения. К этому разделу относят вопросы, связанные с изучением приближения действительных чисел рациональными дробями. К диофантовым приближениям примыкают тесно связанные с этим же кругом идей вопросы изучения арифметической природы различных классов чисел.

) Аналитическая теория чисел. К этому разделу относят вопросы теории чисел, для изучения которых приходится применять методы математического анализа.

В данной курсовой работе мы столкнемся с элементарной теорией чисел, а точнее с элементарной теорией сравнений, её основными свойствами и определениями, которые будут рассмотрены в первой главе.

Во второй главе будет рассмотрен один из важных результатов теории чисел, так называемая китайская теорема об остатках (KTO). По существу эта теорема утверждает, что можно восстановить целое число по множеству его остатков от деления на числа из некоторого набора попарно взаимно простых чисел. Эта теорема в её арифметической формулировке была описана в трактате китайского математика Сунь Цзы «Сунь Цзы Суань Цзин» (кит.упр. 孙子算经 , пиньинь: sunzi suanjing), предположительно датируемом третьим веком н. э. и затем была обобщена Цинь Цзюшао в его книге «Математические рассуждения в 9 главах» датируемой 1247 годом.

Китайская теорема об остатках широко применяется в теории чисел, криптографии и других дисциплинах:

. Взаимно однозначное соответствие между некоторым числом и набором его остатков, определяемым набором взаимно простых чисел, существование которого утверждается в теореме, на практике помогает работать не с длинными числами, а с наборами их коротких по длине остатков. Кроме того вычисления по каждому из модулей можно выполнять параллельно. Если в качестве базиса взять, к примеру, первые 500 простых чисел, длина каждого из которых не превосходит 12 бит, то этого хватит для представления десятичных чисел длиной до 1519 знаков. (Откуда взялось число 1519 понять очень просто: сумма десятичных логарифмов первых 500 простых чисел равна 1519,746…). Например, в алгоритме RSA вычисления производятся по модулю очень большого числа n , представимого в виде произведения двух больших простых чисел. Теорема позволяет перейти к вычислениям по модулю этих простых делителей, которые по величине уже порядка корня из n , а значит имеют в два раза меньшую битовую длину. Отметим также, что применение вычислений согласно китайской теореме об остатках делает алгоритм RSA восприимчивым к атакам по времени.

. На теореме основаны схема Асмута — Блума и схема Миньотта — пороговые схемы разделения секрета в группе участников. Секрет могут узнать только k из n участников, объединив свои ключи.

. Одним из применения является быстрое преобразование Фурье на основе простых чисел

. Теорема лежит в основе принципа Хассе поиска целочисленных корней уравнения.

. Из теоремы следует мультипликативность функции Эйлера.

. На теореме основывается алгоритм Полига-Хеллмана нахождения дискретного логарифма за полиномиальное время для чисел, имеющих специальный вид.

. Теорема имеет множество применений в шифровании и дешифровании в криптографических системах, например, в криптосистеме Рабина или в шифре Виженера.

Глава 1. Элементарная теория сравнений, а ≡ b ( mod p )

. Определения и основные свойства сравнений

В данном параграфе мы рассмотрим целые числа, а обозначать их будем латинскими буквами.

Возьмём произвольное фиксированное натуральное число p и будем рассматривать остатки при делении на р различных целых чисел.

При рассмотрении свойств этих остатков и проведении операций над ними удобно ввести понятие сравнения по модулю.

Определение . Целые числа а и b называются сравнимыми по модулю р, если разность чисел а — b делится на р, то есть, если . Таким образом сравнение представляет собой соотношение между тремя числами a , b и p , причем p ,играющее своего рода эталона сравнения, мы называем модулем. Для краткости мы будем это соотношение между a, b и p записывать следующим образом: a ≡ b ( mod p ), a и b будем называть соответственно левой и правой частями сравнения. Число p , стоящее под знаком модуля, будем всегда считать положительным, т.е запись mod p будет означать, что, числа а и b — вычеты. Если разность а — b не делится на р, то а не сравнимо с b по mod p .

Согласно определению а ≡ 0 ( mod p ) означает, что а делится на р.

≡ 17 ( mod 21)т. к. 101 — 17 = 84, а 84⁞21.

Теорема: число а сравнимо с числом b по модулю p тогда и только тогда, когда а и b имеют одинаковые остатки при делении на р, поэтому в качестве определения сравнения можно взять следующее:

Определение: Целые числа а и b называются сравнимыми по модулю р, если остатки от деления этих чисел на р равны.

Дадим основные свойства сравнений:

. Рефлексивность отношения сравнимости: а ≡ a ( mod p )

.Симметричность отношения сравнимости:

если, а ≡ b ( mod p ) то b ≡ a ( mod p ).

3. Транзитивность отношения сравнимости:

если а ≡ b ( mod p ), b ≡ c ( mod p ), то а ≡ c ( mod p ).

. Если а ≡ b ( mod p ) и k — произвольное целое число, то k а ≡ kb ( mod p )

. Если k а ≡ kb ( mod p ) и ( k , p ) = 1, то а ≡ b ( mod p ).

. Если а ≡ b ( mod p )и k — произвольное натуральное число, то k а ≡ kb ( mod kp )

. Если k а ≡ kb ( mod kp ), где k и р — произвольные натуральные числа, то а ≡ b ( mod p )

. Если а ≡ b ( mod p ), c ≡ d ( mod p ), то а+ c ≡ b + d ( mod p )и а- c ≡ b — d ( mod p ).

. Если а ≡ b ( mod p ), c ≡ d ( mod p ), то а c ≡ bd ( mod p )

. Если а ≡ b ( mod p ), то при любом целом n > 0,а ≡ b ( mod p ).

. Если а ≡ b ( mod p ) и f ( x )= +++. — произвольный многочлен с целыми коэффициентами, то f (а) ≡ f ( b ) ( mod p )

. Любое слагаемое левой или правой части сравнения можно перенести с противоположным знаком в другую часть.

. Если а ≡ b ( mod p ) и , то а ≡ b ( mod d )

. Если а ≡ b ( mod p ), то множество общих делителей а и р совпадает с множеством общих делителей b и р. В частности, ( a , p )=( b , p ).

. Если а ≡ b ( mod ),а ≡ b ( mod )…,а ≡ b ( mod ), то а ≡ b ( mod p ), где p =[,. ].

При делении целого числа на модуль р в остатке получается 0, 1, 2, 3,…,р- 1 чисел.

2. Теорема Эйлера, теорема Ферма

элементарный теорема китайский остаток

Теорема (Эйлера). Пусть m >1,( a , m )=1,  ( m )- функция Эйлера. Тогда: a  ( m )≡1( mod m )

Доказательство. Пусть х пробегает приведенную систему вычетов по mod m :

x =,. rc

где c =  ( m ) их число . — наименьшие неотрицательные вычеты по mod m . Следовательно, наименьшие неотрицательные вычеты, соответствующие числам ax суть соответственно: — тоже пробегают приведенную систему вычетов, но в другом порядке. Значит :

a≡(mod m) a≡(mod m) . arc≡ (mod m), c=φ(m)

Перемножим эти с штук сравнений. Получится:

≡ ( mod m )

Так как ≠0 и взаимно просто с модулем m , то, поделив последнее сравнение на r 1 r 2. rc , получим ).

Теорема (Ферма). Пусть р — простое число, р не делит a . Тогда: a p -1≡1( mod p ).

Доказательство 1. Положим в условии теоремы Эйлера m = p , тогда φ ( m )= p -1. Получаем.

Замечание: Необходимо отметить важность условия взаимной простоты модуля и числа a в формулировках теорем Эйлера и Ферма. Простой пример: сравнение очевидно не выполняется.

Однако можно легко подправить формулировку теоремы Ферма, чтобы снять ограничение взаимной простоты.

Глава 2. Китайская теорема об остатках

. Китайская теорема об остатках

Одним из важных результатов теории чисел является так называемая китайская теорема об остатках (KTO). По существу эта теорема утверждает, что можно восстановить целое число по множеству его остатков от деления на числа из некоторого набора попарно взаимно простых чисел. Эта теорема в её арифметической формулировке была описана в трактате китайского математика Сунь Цзы «Сунь Цзы Суань Цзин» (кит.упр. 孙子算经 , пиньинь: sunzi suanjing), предположительно датируемом третьим веком н. э. и затем была обобщена Цинь Цзюшао в его книге «Математические рассуждения в 9 главах» датируемой 1247 годом, где было приведено точное решение.Существует несколько формулировок данной теоремы, я предоставлю здесь некоторые из них.

Теорема. Пусть , 1 ≤ i ≤ k , взаимно простые числа

и пусть ai целые числа. Тогда существует такое число x ,

что имеет место

x ≡ mod ,

x ≡ ,

x ≡ .

Наконец, рассмотрим еще одну формулировку теоремы,

которую будем использовать в практических работах.

Теорема. Пусть <> — взаимно простые числа и M =

Пусть 0 ≤ ≤ , целые числа. Введем обозначение = . Пусть число, которое удовлетворяет сравнению ≡1 mod .При этих условиях сравнение

x ≡ mod , имеет на интервале [0, M — 1] единственное решение,которое определяется формулой x = + + … +

В рамках условий теоремы китайская теорема об остатках утверждает, что существует взаимно однозначное соответствие между целыми числами и некоторым наборами целых чисел. Другими словами, для каждого целого числа B найдется соответствующий ему единственный набор чисел и наоборот, для каждого набора чисел () найдется единственное соответствующему этому набору число B .

Арифметическая формулировка КТО:

Если числа попарно взаимно просты, то для любых остатков таких, что при всех i = 1,2. n ., найдётся число N , которое при делении на даёт остаток при всех i = 1,2. n .

Применим индукцию по n . При n =1 утверждение теоремы очевидно. Пусть теорема справедлива при n = k -1, т. е. существует число M , дающее остаток при делении на при .Обозначим и рассмотрим числа . Покажем, что хотя бы одно из этих чисел даёт остаток при делении на . Допустим это не так. Поскольку количество чисел равно , а возможных остатков при делении этих чисел на может быть не более чем (ведь ни одно число не даёт остаток ), то среди них найдутся два числа, имеющих равные остатки (принцип Дирихле). Пусть это числа и при и . Тогда их разность делится на , что невозможно, т.к. и взаимно просто с , ибо числа попарно взаимно просты (по условию). Противоречие.

Таким образом, среди рассматриваемых чисел найдётся число , которое при делении на даёт остаток . В то же время при делении на число N даёт остатки соответственно.

Наиболее используемая формулировка КТО:

Пусть — попарно взаимно простые числа и — произвольные целые числа. Тогда существует целое число ,такое что Целое число у удовлетворяет условию тогда и только тогда когда

Доказательство : Обозначим М=и . Тогда числа являются взаимно простыми для всех i. C ледовательно существует целое число такое что где . Положимтогда , поскольку числа . Аналогично доказывается, что . Пусть — остаток от деления числа a на M . Тогда и ≡ a ( mod M ). В частности Далее, пусть целое чисто у удовлетворяет условию . Тогда т. е. Число делится на каждое из чисел .В силу того, что числа попарно взаимно простые, получаем что делится на число . Таким образом, ≡0 ( mod ).Теорема доказана.

2. Примеры. Применение к решению олимпиадных задач

В этом параграфе я опишу один из методов решения систем линейных сравнений. Это очень древний алгоритм. Он применялся еще в античности для решения проблем астрономии. Приведу несколько примеров решения олимпиадных задач и примеров решения сравнений с помощью КТО. Начнем с задачи, сформулированной на современном языке, которая могла бы рассматриваться древними астрономами (Астрономический пример).

Пример 1: Три спутника пересекут меридиан города Лидса сегодня ночью: первый — в 1 ночи, второй — в 4 утра, а третий — в 8 утра. У каждого спутника свой период обращения. Первому на полный оборот вокруг Земли требуется 13 часов, второму — 15, а третьему — 19 часов. Сколько часов пройдет (от полуночи) до того момента, когда спутники одновременно пересекут меридиан Лидса?

Посмотрим, как эта задача переводится на язык сравнений.

Пусть х — количество часов, которые пройдут с 12 часов ночи до момента одновременного прохождения спутниками над меридианом Лидса. Первый спутник пересекает этот меридиан каждые 13 часов, начиная с часу ночи. Это можно записать

как х = 1 + 13 t для некоторого целого t . Другими словами, х ≡ 1 ( mod 13). Соответствующие уравнения для остальных спутников имеют вид: х ≡ 4 ( mod 15) и х≡ 8 ( mod 19). Таким образом, три спутника одновременно пересекут меридиан Лидса через х часов, если х удовлетворяет эти трем уравнениям. Следовательно, для ответа на поставленный вопрос достаточно решить систему сравнений:

х ≡4 ( mod 15), ( B 1)

Заметим, что мы не можем складывать или вычитать уравнения системы, поскольку модули сравнений в них разные. Будем решать эту задачу, переходя от сравнений к уравнениям в целых числах. Так, сравнение х ≡ 1 ( mod 13) соответствует диофантову уравнению: х = 1 + 13 t . Заменяя х во втором сравнении системы на 1 + 13 t , получаем:

+ 13 t ≡ 4 ( mod 15), т.е. 13 t ≡ 3 ( mod 15).

Но 13 обратимо по модулю 15, обратный к нему элемент — это 7. Умножая последнее сравнение на 7 и переходя в нем к вычетам по модулю 15, имеем:

Значит, t может быть записан в виде: t = 6+15 u для какого-то целого u . Следовательно,

х = 1 + 13 t = 1 + 13(6 + 15 u ) = 79 + 195 u .Заметим, что все числа вида 79 + 195 u являются целыми решениями первых двух сравнений системы ( B .1). Наконец, подставим в третье сравнение вместо х выражение 79 + 195 u :

+ 195 u ≡ 8 ( mod 19), так что 5 u ≡ 5 ( mod 19).

Ввиду обратимости остатка 5 по модулю 19, на него можно сократить и увидеть, что

u ≡ 1 ( mod 19). Переписывая это сравнение как диофантово уравнение, мы получим

u = 1 + 19 v для некоторого целого v .

Итак, х = 79 + 195 u = 79 + 195(1 + 19 v ) = 274 + 3705 v .

Какой отсюда можно сделать вывод относительно спутников? Напомним, что х — количество часов, которые пройдут от полуночи до момента одновременного прохождения спутников над меридианом Лидса. Поэтому нам нужно было найти наименьшее натуральное значение переменной х, удовлетворяющее системе ( B .1). Мы это сделали. Поскольку решение системы: х = 274 + 3705 v , то ответ: 274. Итак, спутники одновременно пройдут над меридианом Лидса через 274 часа после 0 часов сегодняшней ночи, что соответствует 11 дням и 10 часам. Но общее решение системы дает больше информации. Прибавляя к 274 любое кратное 3705, мы получаем другое решение системы. Иначе говоря, спутники одновременно пересекают означенный меридиан каждые 3705 часов после первого такого момента, что соответствует 154 дням и 9 часам.

Пример 2 : Найти все целые решения системы сравнений:

Решение: М= 3*5*7=105

Найдем целые числа ,,такие что :

1)*35≡1 (mod 3) *2≡1 (mod 3)

=-1(mod 3)

)*21≡1 (mod 5) *1≡1 (mod 5)

=1

) *15≡1 ( mod 7)

=1

≡ ,

подставим найденные нами значения в формулу:

≡ -1*35*2+ 1*21*3+1*15*2=23, т. е.

Числа вида 23+105 t , где ,исчерпывают все множество решений исходной системы сравнений.

Пример 3 : Доказать что сравнение ≡ 0 ( mod m )разрешимо для каждого натурально числа m >1, несмотря на то, что уравнение =0 не имеет целых решений.

Поскольку =(2 x +1)(3 x +1), то уравнение не имеет решений в кольце . Пусть m =(2 b +1). тогда по китайской теореме об остатках существует целое число х, такое, что 3х≡ -1( mod ) и 2х≡-1( mod (2 b +1)). Следовательно ≡0 ( mod m ).

Пример 4: Доказать что в каждой возрастающей арифметической прогрессии, состоящей из натуральных чисел, существует отрезок произвольной длины, состоящий только из составных чисел.

Рассмотрим арифметическую прогрессию b , b + a , b +2 a ,…, где a , bN , Пусть ,. — простые числа, причем a a ≡- b — aj ( mod ), где j =1,2,…, m . Это означает, что числа b + a (+1), b + a (+2), b + a (+ m ) являются составными.

Пример 5: Доказать что для любых натуральных чисел ,таких что )=)=…=(=1, уравнение имеет бесконечно много натуральных решений. Если n =1,то , — решение уравнения = при любом z .Если n >2, то по китайской теореме об остатках существует бесконечно много таких чисел z , что z ( mod ), z ( mod ). Для каждого такого z числа

,…,,

являются решениями нашего уравнения.

3. КТО. Применение к открытию сейфа в банке

Бенджамен Франклин ( Franklin ) однажды сказал: «Трое могут хранить тайну, если двое из них мертвы». В этом параграфе мы изучаем безопасную систему допуска живых к секретным сведениям, основанную на китайской теореме об остатках. Представьте себе следующую ситуацию

Пусть -попарно взаимно простые числа, такие, что .Пусть S — произвольное целое число с условием M S N и — остатки от деления S на .

Предположим, далее, что в некотором банке работают n кассиров. Кассир с номером i знает пару чисел .Для открытия сейфа необходимо знать ключевое число S . Докажем, что любые k кассиров смогут открыть сейф, но никакие ( k -1) кассиров не смогут это сделать. Действительно, пусть собрались кассиры с номерами , тогда им известен набор чисел По КТО можно найти такое число , что . Так как, то a = S (ввиду единственности решения этой системы сравнений по модулю) и ключевое число найдено, т.е. сейф можно открыть. Если собрались ( k -1) кассиров, то они знают пары чисел. По КТО они могут найти такое целое число b , что и , т. е. b ≠ S . Таким образом, b не является искомым ключом к открытию сейфа.

В качестве конкретного примера можно рассмотреть числа : и,например, S =4001. Каждый из пяти кассиров знает одну из пар чисел (5,9), (1.10), (32,49), (32,53),(48,59).

Из предыдущего следует, что любые три кассира смогут найти ключ (равный S =4001) и открыть сейф, но никакие два не смогут этого сделать.

В выше приведённой работе была сформулирована китайская теорема об остатках, приведены её доказательства, а также указанно применение КТО к решению олимпиадных задач и к некоторым прикладным вопросам теории чисел.

1. Бухштаб А.А. Теория чисел. — М: Просвящение,1996.

. Кузьмина А.С., Мальцев Ю.А. Теория чисел: учебное пособие/ А.С. Кузьмина, Ю.Н. Мальцев. — Барнаул: АлтГПА,2011.-240с.

. Коутинхо С. Введение в теорию чисел. Алгоритм RSA . Москва: Постчаркет, 2001. — 328 с.

. Рыбников К.А. История математики: учебное пособие для университетов-Издательство Московского Университета,1960.