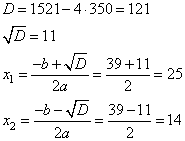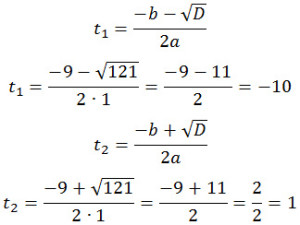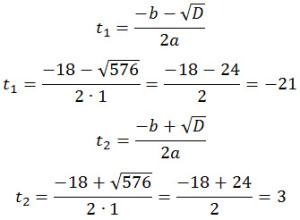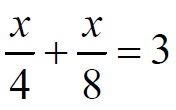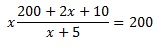ОГЭ 2018. Алгебра. 2 часть, задание №21 с решением.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Задание 21. Решите уравнение
Решение. 1. Найдем один из корней кубического уравнения. Для этого рассмотрим числа 1; -1 и 3; -3 (наименьшие делители свободного члена кубического уравнения). Путем подстановки каждого из этих числе вместо x, проверим, является ли один из них корнем (для этого уравнение должно быть равно 0):
— для x=1: 
— для x=-1: 
— для x= 3: 
2. Теперь выполним деление кубического многочлена на x-3, воспользовавшись схемой Горнера, имеем:
3. Получаем квадратное уравнение для вычисления оставшихся двух корней:

Получили три корня 3; -3; -4. Ответ: 3; -3; -4.
Задание 21. Решите уравнение
1. Найдем один из корней кубического уравнения. Для этого рассмотрим числа 1; -1 и 2; -2 (делители свободного члена кубического уравнения). Путем подстановки каждого из этих чисел вместо x, проверим, является ли один из них корнем (для этого уравнение должно быть равно 0):
— для x=1: 
2. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
3. Получаем квадратное уравнение для вычисления оставшихся двух корней:

Задание 21. Решите уравнение
Решение. 1. Найдем один из корней кубического уравнения. Для этого рассмотрим числа 1; -1 и 3; -3 (делители свободного члена кубического уравнения). Путем подстановки каждого из этих чисел вместо x, проверим, является ли один из них корнем (для этого уравнение должно быть равно 0):
— для x=1: 
— для x=-1: 
— для x=3: 
2. Теперь выполним деление кубического многочлена на x-3, воспользовавшись схемой Горнера, имеем:
3. Получаем квадратное уравнение для вычисления оставшихся двух корней:

Задание 21. Решите уравнение
1. Извлечем кубический корень из левой и правой частей уравнения, получим:
2. Решаем квадратное уравнение, получаем два корня:
Задание 21. Решите уравнение
Возьмем корень третьей степени из обеих частей уравнения, получим:
Решим квадратное уравнение:
Задание 21. Решите уравнение
Возьмем корень кубической степени от обеих частей уравнения, получим:
Решаем квадратное уравнение, имеем два корня:
Задание 21. Решите уравнение 
Решение. 1. Запишем ОДЗ уравнения:

2. Упросим уравнение и найдем его корни:
Решаем квадратное уравнение, получаем:

Из двух корней только один x=-3 удовлетворяет ОДЗ. Ответ: -3.
Задание 21. Решите уравнение 
1. Запишем ОДЗ уравнения:

2. Упростим уравнение, получим:
Решаем квадратное уравнение, получаем корни:
Только один корень x=-4 удовлетворяет ОДЗ.
Задание 21. Решите уравнение x^3 + 6x^2 = 4x + 24.
Решение. Упростим выражение, приведем его к виду:
Данное выражение равно 0, если хотя бы один из сомножителей равен 0, то есть имеем два уравнения:

Получаем три корня: -6; -2; 2.
Задание 21. Решите уравнение x^3+4x^2 = 9x +36.
Решение. Сначала преобразуем выражение: в левой части вынесем 
Последнее выражение будет равно нулю, если хотя бы один из множителей равен нулю. То есть, имеем два уравнения:

Задание 21. Сократите дробь 
Заметим, что число 

Задание 21. Сократите дробь 
Учитывая, что 

Задание 21. Решите систему уравнений
Решение. Для решения данной системы можно вычесть второе уравнение из первого, это позволит избавиться от переменной y, получим:

Для каждого из найденных корней найдем соответствующее значение y, подставив 


Задание 21. Решите систему уравнений
Решение. Так как оба уравнения равны одному и тому же значению y, то их можно приравнять, получим:



Найдем теперь значения y для каждого x, имеем:

Задание 21. Решите систему уравнений
Решение. Разделим первое уравнение на 2, а второе – на 4, получим:





Таким образом, имеем решение (2, -2), (2,2). Ответ: (2, -2), (2,2).
Задание 21. Решите систему уравнений
Решение. Разделим второе уравнение на 2, получим систему



Задание 21. Решите уравнение
Решение. Преобразуем уравнение, приведем его к следующему виду:
Полученное выражение будет равно 0, если 
Таким образом, получили следующие корни: -4; -3; 2. Ответ: -4; -3; 2.
Задание 21. Решите уравнение 
Решение. Упростим выражение, перепишем его в следующем виде:
Полученное выражение будет равно 0, если 
Получили три корня: -5; -4; -3.
Задание 21. Решите систему уравнений
Сложим оба уравнения, получим:
Для найденных корней x вычислим из первой формулы соответствующие значения y, имеем:
— для 

— для 

Получили два решения: (-1;5), (1;5).
Задание 21. Решите систему уравнений
Сложим оба уравнения, получим:
Вычислим соответствующие значения y при x=-2 и 2, подставив эти значения в первую формулу системы:
— при x=-2: 
— при x=2: 
Имеем следующие решения: (-2; 3) и (2; 3).
Задание 21. Решите неравенство 
Решение. Можно заметить, что данное неравенство будет больше либо равно 0, если

Из последнего выражения имеем две точки, делящие числовую ось:




Ответ: 
Задание 21. Решите неравенство 
Решение. Из неравенства можно видеть, что оно будет соблюдаться, если

Перепишем его в следующем виде:
Последнее выражение дает две точки, делящие числовую ось:



Ответ: 
Задание 21. Решите неравенство
Сложим оба уравнения системы, избавимся таким образом от переменной y, получим:
Теперь, для каждого из найденных x, вычислим y из первого уравнения:
Получаем решения: (-1; 8), (1; 8).
Задание 21. Решите неравенство
Сложим оба уравнения системы, избавимся от переменной y, получим:
Для каждого найденного корня x вычислим соответствующее значение y из первого уравнения, имеем:
То есть получили следующие решения: (-2; 1), (2; 1).
Задание 21. Найдите значение выражения 28a-7b+40, если 
Приведем выражение 

Ответ: 5.
Задание 21. Найдите значение выражения 33a-23b+71, если 
Приведем выражение 

Задание 21. Решите уравнение 
Решение. Учитывая, что слагаемые в уравнении всегда больше либо равны 0, то уравнение будет равно нулю, если каждое из слагаемых равно нулю. Соответственно, получаем следующую систему уравнений:

Из второго уравнения, получаем следующие два корня:
Из полученных значений видно, что оба уравнения одновременно будут принимать значение 0 при x=-5.
Задание 21. Решите уравнение 
Решение. Любое число в квадрате всегда больше 0, следовательно, уравнение будет равно 0, если оба слагаемых равны 0. Это условие можно записать в виде следующей системы:

Из второго уравнения, имеем корни:
Общий корень, при котором оба уравнения переходят в 0, равен -4. Ответ: -4.
Задание 21. Решите уравнение 
Упростим уравнение, приведем его к следующему виду:
Данное уравнение будет равно 0, если
Решаем первое квадратное уравнение, получаем корни:
Оба корня удовлетворяют неравенству 
Ответ: 
Задание 21. Решите уравнение 
Преобразуем уравнение к виду
Данное уравнение будет равно 0, если
Найдем корни уравнения из квадратного уравнения:
Оба корня не равны 0, следовательно, являются решениями уравнения.
Ответ: 
Задание 21. Решите уравнение 
Сначала преобразуем выражение, получим:
Последнее выражение показывает, что уравнение будет равно 0, если хотя бы один из множителей будет равен 0, то есть имеем 3 уравнения и 3 корня:
Задание №21 ОГЭ по математике
В двадцать втором задании необходимо решить задачу, составив уравнение с неизвестными. Ниже мы приводим алгоритмы решения типовых вариантов.
Алгоритм решения:
- Введем неизвестную величину: скорость третьего.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Выясняем, на какой
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Решение:
1. Обозначим через x км/ч скорость третьего велосипедиста. 2. Составим таблицу их краткого условия:
| v, км/ч | t, ч | S, км |
| 1 велосипедист | 21 | На 2 ч раньше всех |
| 2 велосипедист | 15 | На 1 ч раньше третьего |
| 3 велосипедист | х |
3. Задача на движение водном направлении, значит, для определения совместной скорости (сближения), необходимо из большей скорости вычитать меньшую. Наибольшая скорость была у третьего велосипедиста, потому что он догонял двух других.
4. Перед тем, как выехал третий велосипедист, первый двигался уже 2 часа. За это время он проехал 42 км, а второй проехал 15 км, поскольку был в пути 1 час. Совместная скорость третьего и второго велосипедистов равна (x-15) км/ч. так как они движутся в одном направлении. Третий велосипедист догнал второго спустя 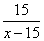
Совместная скорость третьего и первого велосипедистов равна (x-21)км/ч. Третий велосипедист догнал первого через 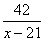
По условию третий велосипедист догнал первого спустя 9 ч после того, как догнал второго.
5. Исходя из этого, составим равенство:
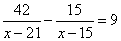
Преобразуем полученное уравнение:
6. Получили квадратное уравнение. Решим его:
По условию скорость третьего велосипедиста была наибольшей, значит, второй
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста.
2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км |
| 1 велосипедист | 15 | t +7 |
| 2 велосипедист | 10 | t +1 |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км.
Скорость второго велосипедиста 10 км/ч. В пути он находился t + 1 часов к моменту встречи с третьим велосипедистом. Тогда в момент встречи велосипедисты находились на расстоянии 10·(t + 1) км от поселка. Расстояния эти одинаковы, значит, x·t = 10·(t + 1).
Первого велосипедиста третий догонит через t + 5 ч – время, за которое он догнал первого велосипедиста после второго, тогда до места встречи с первым велосипедистом третий проехал x·(t + 5) км.
Первый велосипедист ехал со скоростью 15 км/ч и был в пути до встречи с третьим t + 7 часов, потому как выехал он на 2 часа раньше. Расстояние, которое проехал первый велосипедист, равно 15·(t + 7) км.
Получаем еще одно равенство: x·(t + 5) = 15·(t + 7)
4. Составляем систему уравнений:
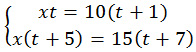

Подставляем вместо x в первое уравнение системы правую часть равенства и решаем полученное уравнение.
(t + 19)·t = 10t + 10
t 2 + 19t = 10t + 10
По формуле дискриминанта и корней:
D = 9 2 — 4·1·(-10) = 81 + 40 = 121
Первый ответ не может удовлетворять условию задачи, поскольку время не может иметь отрицательных значений. Следовательно,
x = t + 19 = 1 + 19 = 20
Скорость третьего велосипедиста 20 км/ч.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста. 2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км |
| 1 велосипедист | 24 | t +9 |
| 2 велосипедист | 21 | t +1 |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км. Второй велосипедист до момента, когда его догонит третий велосипедист, двигался t + 1 часов . Он проехал до места встречи 21·(t + 1) км. Расстояния, пройденные велосипедистами, одинаковы. Получим первое равенство x·t = 21·(t + 1). Третий велосипедист до момента встречи с первым велосипедистом после встречи о вторым, ехал t + 9 ч тогда до места встречи с первым велосипедистом он проехал расстояние x·(t + 9) км. Первый велосипедист до встречи с третьим ехал t + 11 часов, поскольку до момента выезда третьего, уже проехал 2 часа. До места встречи он проехал 24·(t + 11) км. Расстояния одинаковы. Тогда получим еще одно равенство: x·(t + 9) = 24·(t + 11) Составим систему уравнений для решения задачи: 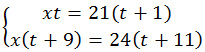
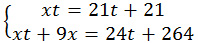
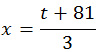
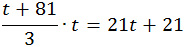
t 2 + 81t = 63t + 63
t 2 + 18t – 63 = 0
D = 18 2 — 4·1·(-63) = 324 + 252 = 576
Первое значение не подходит, поскольку время по условию не может иметь отрицательные значения. Значит, 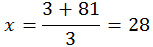
pазбирался: Даниил Романович | обсудить разбор | оценить
Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно
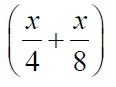
Из условия задачи следует, что это время равно 3 часам. Составим уравнение:
Решая уравнение, получаем x = 8.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Находим число процентов (или долю) твердого вещества в свежих фруктах. Находим эту величину в кг.
- Вычисляем кол-во процентов твердого вещества в сушеных фруктах.
- Составляем пропорцию и определяем общую массу сушеных фруктов.
Решение:
В сушеных фруктах масса твердого вещества, по сравнению со свежими, не меняется (а только снижается объем воды). Поэтому в искомой массе сухих фруктов мякоти тоже будет 4,2 кг. Но в процентном соотношении эта масса составит 100%–30%=70% (30% по условию приходится на воду). Искомая же (общая) масса сухих фруктов в данном случае – это 100%.
Тогда обозначим искомую массу через Х и составим пропорцию: 4,2 кг – 70% Х – 100%
Решим эту пропорцию:
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Вводим переменные-обозначения для скорости наполнения резервуара (л/мин) и для времени наполнения (мин). Выражаем через соответствующие переменные параметры наполнения для 1-й и 2-й труб.
- Составляем систему уравнений (1-е уравнение для первой трубы, 2-е – для второй).
- Решаем систему.
Решение:
Обозначим через х скорость наполнения 1-й трубы (это наша искомая величина). Тогда скорость наполнения 2-й трубы равна (х+5).Обозначим через t время наполнения 2-й трубы. Тогда время наполнения 1-й трубы составит (t+2).
Через каждую из труб должно пройти 200 л воды. Для 1-й трубы получим:
Аналогично для 2-й трубы:
Из уравнения для 2-й трубы выразим t через х:
Подставим полученное для t выражение в уравнение для 1-й трубы: 
Корень х2 не может быть принят в качестве ответа, поскольку он не удовлетворяет условию (скорость наполнения резервуара не может быть отрицательной величиной).
Значит, искомая скорость наполнения равна 20 л/мин.
pазбирался: Даниил Романович | обсудить разбор | оценить
Составим для удобства решения таблицу, в которую внесем данные из условия задачи, обозначив переменной х неизвестную величину – скорость 1 автомобиля:
| Скорость | Время | Расстояние | |
| 1 автомобиль | х | 800 х . . | 800 |
| 2 автомобиль | х – 36 | 800 х − 36 . . | 800 |
Пояснения к заполнению таблицы:
Так как мы обозначили за х скорость 1 авто, значит скорость 2 авто будет на 36 км/ч меньше.
Расстояние у каждого авто будет 800 км.
Для нахождения времени надо расстояние разделить на скорость, поэтому мы получили дроби с переменной в знаменателе.
Зная, что первый прибывает к финишу на 5 ч раньше второго, составим и решим уравнение:
800 х − 36 . . − 800 х . . = 5
Приведем к общему знаменателю х(х-36) наше уравнение и решим его:
800х – 800х+28800=5х 2 – 180
5х 2 – 180 – 28800 =0; разделим на 5 каждый коэффициент:
Решим полученное квадратное уравнение
D=b 2 – 4ac=36 2 – 4 ∙ ( − 5760 ) =24336
х1,2= − b ± √ D 2 a . . = 36 ± 156 2 . .
Отсюда х1=96, а х2 не удовлетворяет условию задачи, так как оно отрицательное, а скорость не может быть выражена отрицательным числом.
Значит, скорость первого автомобиля 36 км/ч
pазбирался: Даниил Романович | обсудить разбор | оценить
ОГЭ по математике: 2 часть
Смотрите бесплатные видео-уроки по теме “ОГЭ 2 часть” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
На этой странице я буду публиковать бесплатные видео-уроки по теме 2 часть ОГЭ по математике.
Задание 21: уравнения
Для того, чтобы научиться решать уравнения в 21 задании во 2 части ОГЭ по математике необходимо сначала научиться решать самые простые уравнения:
http://spadilo.ru/zadanie-21-oge-po-matematike/
http://epmat.ru/oge-po-matematike-2-chast/