Решить систему уравнений в языке с

BestProg

Разработка приложения решения системы линейных алгебраических уравнений методом Гаусса

Условие задачи

Задана система линейных алгебраических уравнений:

Разработать приложение, которое осуществляет решение системы линейных алгебраических уравнений с помощью метода Гаусса. Работа приложения должна быть реализована в виде мастера, в котором информация для каждого следующего шага определяется из информации на предшествующем шаге.

Выполнение

При сохранении проекта имя модуля главной формы приложения оставляем по умолчанию « Unit1.cpp «.

Рис. 1. Форма приложения с созданными файлами

2. Разработка главной формы приложения

2.1. Название приложения

Задать название приложения. Для этого свойство Caption главной формы устанавливаем в значение «Метод Гаусса».

2.2. Установка свойств формы

Выделить форму. В Object Inspector установить значение следующих свойств:
– свойство Border Style = bsDialog ;
– свойство Position = poScreenCenter ;
– в свойстве Font выбрать параметры шрифта: шрифт Tahoma , размер шрифта 12 (рис. 2).

Рис. 2. Установка параметров шрифта главной формы приложения

В результате, форма приложения примет вид как показано на рисунке 3.

Рис. 3. Главная форма приложения

2.3. Компонент типа TGroupBox

Размещаем на форме компонент (элемент управления) типа TGroupBox из палитры компонент « Tool Palette «.

Рис. 4. Компонент типа TGroupBox

В результате, система создаст объект-переменную с именем GroupBox1 .

Изменяем размеры компонента GroupBox1 на всю ширину окна главной формы.

Свойство Caption компонента GroupBox1 устанавливаем в значение « Условие задачи «. Форма приложения будет иметь вид, как показано на рисунке 5.

Рис. 5. Форма приложения после размещения компонента TGroupBox

2.4. Компонент типа TLabel .

Размещаем компонент типа TLabel в области компонента TGroupBox . Автоматически создается объект-переменная с именем Label1 (рис. 6).

Устанавливаем свойство WordWrap компонента Label1 в значение « true » (рис. 6).

С помощью мышки изменяем ширину вывода текста компонента Label1 (рис. 6).

Рис. 6. Компонент Label1 , свойство WordWrap

Свойство Caption компонента Label1 устанавливаем в значение:

Решить систему линейных алгебраических уравнений методом Гаусса

В результате, форма приложения примет вид, как показано на рисунке 7.

Рис. 7. Форма приложения после размещения компонента Label1

2.5. Компоненты типа TButton .

Размещаем на форме компоненты типа TButton . В результате образуются два объекта-переменные с именами Button1 и Button2 .

Для лучшей наглядности изменяем размеры компонент так как показано на рисунке 8.

Рис. 8. Форма приложения с размещенными компонентами Button1 и Button2

Устанавливаем такие свойства компонент Button1 и Button2:
– в компоненте Button1 свойство Caption = «Выход» ;
– в компоненте Button2 свойство Caption = «Расчет >>» .

В результате форма приложения примет вид, как показано на рисунке 9.

Рис. 9. Главная форма приложения после размещения всех компонент

3. Программирование события клика на кнопке «Выход».

Вызовем событие OnClick компонента Button1 (кнопка « Выход «) (рис. 10). Событие размещается на вкладыше Events в Object Inspector .

Процесс программирования события OnClick подробно описан здесь.

Рис. 10. Вызов события OnClick компонента Button1

В результате, откроется окно с программным кодом метода обработки события. Между скобками < >вводим вызов метода Close() .

Метод Close() закрывает окно главной формы приложения и осуществляет все необходимые операции по освобождению памяти, ресурсов и т.д.

Листинг метода обработки события следующий:

4. Разработка формы ввода числа уравнений n.

4.1. Размещение компонент на форме и их настройка.

Процесс создания новой формы подробно описан здесь.

Для создания новой формы вызовем команду

В результате, будет создана новая форма, как показано на рисунке 11. Сохраняем форму под именем « Unit2.cpp «.

Создаются файлы, которые соответствуют форме:
– файл « Unit2.h «, содержащий описания глобальных переменных и подключения других модулей;
– файл « Unit2.cpp «, содержащий реализацию методов формы;
– файл « Unit2.dfm «, содержащий описание изображения формы на экране (размеры окна, координаты формы относительно окна экрана, значение цветов и прочее).

Новосозданной форме отвечает объект с именем Form2 . С помощью этого имени можно приступаться к свойствам и методам формы Form2 .

Рис. 11. Новосозданная форма Form2

Осуществим настройку формы Form2 .

Сначала настроим свойства формы:
– свойство Caption = «Задайте число уравнений» ;
– свойство BorderStyle = bsDialog ;
– свойство Position = poScreenCenter ;
– в свойстве Font нужно выбрать следдующие параметры шрифта: шрифт Tahoma, размер шрифта 12.

Размещаем на форме такие компоненты:
– компонент типа TGroupBox которому будет отвечать объект GroupBox1;
– компонент типа TLabel, размещается внутри области компонента GroupBox1 . Компоненту типа TLabel отвечает объект-переменная Label1 ;
– компонент типа TEdit , размещается внутри области компонента GroupBox1 . Этому компоненту отвечает объект (переменная) Edit1 ;
– два компонента типа TButton , которым отвечают объекты с именами Button1 и Button2 .

Осуществим настройку свойств компонент:
– в компоненте GroupBox1 значение свойства Caption = «» (пустая строка);
– в компоненте Label1 значение свойства Caption = «n = « ;
– в компоненте Edit1 значение свойства Text = «» ;
– в компоненте Button1 значение свойства Caption = « ;
– в компоненте Button2 значение свойства Caption = «Далее >>» .

После размещения компонент и корректирования размеров формы, форма Form2 имеет вид как показано на рисунке 12.

Рис. 12. Форма Form2 после размещения и настройки всех компонент

4.2. Программирование обработчиков событий формы Form2 .

В форме Form2 программируем два обработчика событий:
– обработчик события OnClick клика на кнопке « «;
– обработчик события OnClick клика на кнопке « Далее >> «.

Листинг обработчика события клика на кнопке Button1 (« «):

Листинг обработчика события клика на кнопке Button2 (« Продолжить >> «):

Глобальная переменная ModalResult отвечает за состояние формы. Если глобальная переменная ModalResult=0 , то это означает что форма открытая как модальное окно. Как только значение ModalResult станет ненулевым, то форма Form2 закроется с кодом возврата, помещенным в ModalResult .

Таким образом, если пользователь сделает клик на кнопке Button1 , то форма Form2 закроется с кодом возврата mrNo. Если пользователь сделает клик на кнопке Button2, то форма Form2 закроется с кодом возврата mrOk .

5. Построение формы ввода коэффициентов в уравнениях.

5.1. Размещение компонент на форме и их настройка.

Создание формы происходит стандартным путем и описано в п. 4.

Сохраняем форму под именем предлагаемым по умолчанию « Unit3.cpp «.

После создания формы получим объект с именем Form3 . С помощью этого объекта можно будет использовать методы и свойства формы Form3 .

Данной форме отвечают файлы с именами « Unit3.h «, « Unit3.cpp » и « Unit3.dfm «.

Сначала осуществим настройку свойств формы Form3 так, как описано в п. 4:
– свойство Caption = «Ввод коэффициентов уравнений «;
– свойство BorderStyle = bsDialog ;
– свойство Position = poScreenCenter ;
– в свойстве Font нужно выбрать параметры шрифта: шрифт Tahoma , размер шрифта 12 .

Для построения формы ввода коэффициентов уравнений используем такие компоненты:
– два компонента типа TLabel . Автоматически будут созданы объекты с такими именами: label1 и label2 ;
– компонент типа TStringGrid (рис. 13) для ввода коэффициентов, которые размещаются в левой части системы уравнений.

Компонент TStringGrid размещается во вкладке Additional панели инструментов « Tool Palette «. Создается объект с именем StringGrid1 ;
– компонент типа TStringGrid (рис. 13) для введения коэффициентов, которые размещаются в правой части системы уравнений. Создается объект с именем StringGrid2 ;
– два компонента типа TButton (кнопки « » и « Продолжить >> «). Создаются два объекта с именами Button1 и Button2 .

Рис. 13. Компонент TStringGrid на палитре компонент

После размещения компонент и корректировки их размеров, форма Form3 будет иметь приблизительно следующий вид (рис. 14).

Рис. 14. Форма Form3

Формируем свойства компонент формы Form3:
– в компоненте Label1 свойство Caption = « Коэффициенты в левой части уравнения «;
– в компоненте Label2 свойство Caption = «Правая часть» ;
– в компоненте Button1 свойство Caption = « ;
– в компоненте Button2 свойство Caption = «Далее >>» .

Формируем свойства компонентов типа TStringGrid :
– в компоненте StringGrid1 свойство FixedCols = 0 (число фиксированных колонок);
– в компоненте StringGrid1 свойство FixedRows = 0 (число фиксированных строк);
– в компоненте StringGrid2 свойство FixedCols = 0 ;
– в компоненте StringGrid2 свойство FixedRows = 0 ;
– в компоненте StringGrid1 выбираем вкладку Options и устанавливаем опцию goEditing в значение « true «;
– в компоненте StringGrid2 во вкладке Options опция goEditing = « true «.

Рис. 15. Установление опции goEditing во вкладке Options компонента StringGrid1

После выполненных действий, форма Form3 будет иметь вид как показано на рисунке 16.

Рис. 16. Форма Form3 после окончательного формирования

5.2. Программирование обработчиков событий формы Form3 .

Программируем обработчики событий OnClick клика на кнопках Button1 и Button2 формы Form3 .

Листинг обработчиков событий приведен ниже.

6. Создание формы вывода результата.

Последней в приложении создается форма, которая будет выводить результат вычислений. Процесс создания и сохранения формы подробно описан здесь. При сохранении формы оставляем имя по умолчанию « Unit4.cpp «.

В результате получаем объект с именем Form4 .

Новосозданная форма Form4 описывается в файле « Unit4.dfm «. Также форме отвечают файлы « Unit4.h » и « Unit4.cpp «.

6.1. Построение формы Form4 .

Сначала настраиваем свойства формы Form4 :
– свойство Caption = «Результат» ;
– свойство BorderStyle = bsDialog ;
– свойство Position = poScreenCenter ;
– в свойстве Font нужно выбрать следующие параметры шрифта: шрифт Tahoma , размер шрифта 12 .

Также корректируем размеры формы.

Следующим шагом идет размещение на форме компонент.

Размещаем на форме следующие компоненты (рис. 17):
– один компонент типа TLabel ;
– два компонента типа TStringGrid ;
– один компонент типа TButton .

Корректируем размеры и позиции компонент для удобного отображения.

После размещения компонент будут созданы объекты с такими именами: Label1 , StringGrid1 , StringGrid2 , Button1 . В компоненте StringGrid1 выводятся номера переменных величин x в уравнении. В компоненте StringGrid2 выводятся значения решения системы уравнений.

Настраиваем компоненты формы следующим образом:
– в компоненте Label1 свойство Caption = «Решение системы» ;
– в компоненте Button1 свойство Caption = «OK» ;
– в компоненте StringGrid1 свойства FixedCols = 0 и FixedRows = 0 ;
– в компоненте StringGrid2 свойства FixedCols = 0 и FixedRows = 0 .

После размещения и настройки компонент, форма Form4 будет иметь вид, как показано на рисунке 17.

Рис. 17. Форма Form4 после окончательного формирования

6.2. Программирование события клика на кнопке « ОК » формы Form4 .

Листинг обработчика события клика на кнопке « ОК » следующий:

7. Написание программного кода расчета.

7.1. Подключение модулей «Unit2.h», «Unit3.h», «Unit4.h» к модулю «Unit1.h».

Для того, чтобы из главной формы приложения Form1 вызвать второстепенные формы, нужно осуществить их подключения в модуле « Unit1.h «.

Подключение модулей форм Form2 , Form3 , Form4 к форме Form1 осуществляется стандартным для языка C/C++ способом.

Сначала нужно перейти в модуль « Unit1.h «.

Затем после строк

Сопромат .in.ua

изучаем сопротивление материалов

Некоторые варианты решения системы уравнений

Решение online

На странице “Решение системы линейных уравнений“ вы можете решить систему до 10 уравнений online.

Решение системы линейных алгебраических уравнений в OpenOffice.org

Из линейной алгебры нам известно, что для системы линейных уравнений A*x=b решением 1 есть x=A -1 *b, если детерминант матрицы A не равен нулю. Здесь A -1 – обратная матрица коэффициентов СЛАУ .

Решим систему из двух уравнений.

В ячейках (A1:B2) вводим данные.
Детерминант матрицы: MDETERM(A1:B2)

Затем получаем обратную мартицу A -1 :
=

Умножаем полученную обратную матрицу на столбик з правою частью систем уравнений:
=

Осталось проверить проверить правильность решения, подставив полученные неизвестные в систему уравнений.

Пример решения системы линейных уравнений в Scilab

Scilab — мощный открытый пакет прикладных математических программ (система компьютерной математики) для инженерных и научных расчётов.

решать задачи линейной алгебры;
решать нелинейные уравнения и системы;
решать задачи оптимизации;
дифференцировать и интегрировать;
решать обыкновенные дифференциальные уравнения и системы.
обрабатывать экспериментальные данные (интерполяция и аппроксимация, метод наименьших квадратов);
создавать различные виды графиков и поверхностей.

Более подробно с пакетом можно ознакомится на домашней странице Scilab или в википедии

Пример

Решим систему из двух уравнений вида A*x=b

Задаем матрицу коэффициентов: —>A=[1,2;3,4] A = 1. 2. 3. 4. Задаем вектор свободных коэффициентов: —>b=[2;1] b = 2. 1.

Определяем детерминант матрицы: —>det(A) ans = — 2 Так как определитель матрицы отличен от нуля, решение СЛАУ существует.

Решение СЛАУ методом обратной матрицы —>x=A\b x = — 3. 2.5 Запись A\b соответствует математической операции A -1 b. Записи x=A\b эквивалентна запись x=inv(A)*b

Эту систему уравнений также можно решить с помощью специальной функции linsolve (эта функция решает уравнение вида Ax+b=0, поэтому поменяем знак вектора b) x=linsolve(A,-b) x = — 3. 2.5 и получили ответ: x₀= -3; x₁= 2.5;

Проверяем A*x-b ans = 1.0D-14 * 0.2220446 0.3552714 результирующий вектор близок к нулю, то есть система решена верно.
Существуют и другие способы решения системы линейных уравнений в среде Scilab.

Пример решения системы линейных уравнений в среде программирования R

R — язык программирования для статистической обработки данных и работы с графикой, а также свободная программная среда вычислений с открытым исходным кодом.

Пример

Решаем систему Ax=b (из двух уравнений)

A A [,1] [,2] [1,] 1 2 [2,] 3 4 > b b [1] 2 1 > x x [1] -3.0 2.5 и получили ответ: x₁= -3; x₂= 2.5;

Проверка: > A %*% x [,1] [1,] 2 [2,] 1

Определитель матрицы: > det(A) [1] -2

Решение системы линейных уравнений Ax=b в Euler Math Toolbox

Домашняя страница Euler Math Toolbox . В пакет интегрирована система компьютерной алгебры Maxima. Система напоминает Matlab, но имеет собственный стиль, и немного иной синтаксис.
Домашняя страница автора René Grothmann

Пример

This is Euler Math Toolbox, Version 5.8. >A:=[1,2;3,4] 1 2 3 4 >b:=[2;1] 2 1 >x:=A\b -3 2.5 Получили ответ: x₀= -3; x₁= 2.5;

Определитель матрицы: >det(A) -2

Проверка: умножим A на x (операция умножения обозначается точкой «.») >A.x 2 1

Решить указанную систему можно также с помощью следующего выражения (inv(A) — обратная матрица) >x:=inv(A).b -3 2.5

1 Этот способ решения называется — решение СЛАУ методом обратной матрицы

Решение системы линейных уравнений

Министерство образования и науки Республики Беларусь

Белорусский государственный университет

информатики и радиоэлектроники

Факультет информационных технологий и управления

Кафедра Вычислительных Методов и Программирования

к курсовой работе

«Решение системы линейных уравнений»

ст.гр.020603 Навроцкий А.А.

1. Анализ существующих методов решения задачи.

2. Описание используемого метода.

3. Анализ результатов.

Список использованной литературы.

Приложение (распечатка программы, результатов).

Решение систем линейных алгебраических уравнений (СЛАУ) является одной из основных задач линейной алгебры. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.

Применяемые на практике численные методы решения СЛАУ делятся на две группы — прямые и итерационные.

В прямых (или точных) методах решение системы получают за конечное число арифметических действий. К ним относятся известное правило Крамера нахождения решения с помощью определителей, метод последовательного исключения неизвестных (метод Гаусса) и его модификации, метод прогонки и другие. Сопоставление различных прямых методов проводится обычно по числу арифметический действий, необходимых для получения решения. Прямые методы являются универсальными и применяются для решения систем до порядка 10 3 . Отметим, что вследствие погрешностей округления при решении задач на ЭВМ прямые методы на самом деле не приводят к точному решению системы.

Итерационные (или приближенные) методы являются бесконечными и находят решение системы как предел при k®¥ последовательных приближений x ( k ) , где k — номер итерации. Обычно задается точность e, и вычисления проводятся до тех пор, пока не будет выполнена оценка ºx ( k ) – x ( k -1) º 2 числовым равенствам

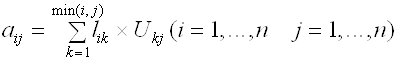
Разложение матрицы A на множители обычно получают посредством алгоритма, который называется компактной схемой метода Гаусса. Элементы l_i_m и U_m_i могут быть вычислены по формулам

Тогда решение системы Ax=b сводится к последовательному решению двух систем — Ly=b и Ux=y.

Рассмотренный метод можно применять к решению серии систем с одной и той же матрицей.

Метод простых итераций (Якоби).

Для решения итерационным методом система линейных алгебраических уравнений Ax = b должна быть приведена к виду x = Gx+f , где G — некоторая матрица, f — преобразованный вектор свободных членов. Затем выбирается начальное приближение — произвольный вектор x (0) — и строится рекуррентная последовательность векторов x (1) , x (2) . x ( k ) . по формуле

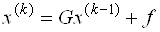
Для сходимости этой последовательности при любом начальном приближении необходимо и достаточно, чтобы все собственные значения матрицы G были по абсолютной величине меньше единицы. На практике это трудно проверить, и обычно пользуются достаточными условиями сходимости — итерации сходятся, если какая-нибудь норма матрицы меньше единицы, т.е.

или .

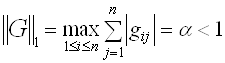
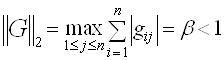
Чем меньше норма матрицы G, тем быстрее сходится итерационный процесс.

Преобразование системы можно осуществить, просто решая каждое i-е уравнение относительно x_i :

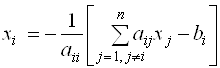
Метод Якоби использует следующий алгоритм построения приближений:

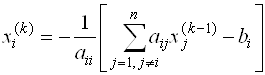
Если A — матрица с доминирующей диагональю, т.е. 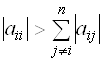, то метод Якоби сходится при любом начальном приближении x (0 ) .

Метод Якоби относится к одношаговым итерационным методам, когда для нахождения x ( k +1) требуется помнить только одну предыдущую итерацию x ( k ) . Для исследования сходимости удобнее записывать итерационные методы не в координатной, а в матричной форме, придерживаясь стандартной формы записи итерационных методов.

Канонической формой одношагового итерационного метода решения СЛАУ называется его запись в виде

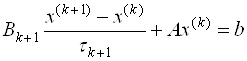
где B_k+1 — матрица, задающая тот или иной итерационный метод, t_k+1 — итерационный параметр. Числовые параметры t_k вводят для ускорения сходимости. Способ выбора итерационных параметров определяется при исследовании сходимости метода, когда выясняется при каких значениях параметров метод сходится и когда сходимость будет наиболее быстрой (соответствующие параметры называются оптимальными).

Итерационный метод называют явным, если B_k+1 — единичная матрица. Неявные итерационные методы имеет смысл применять лишь в том случае, когда решение системы уравнений с матрицей B_k требует меньше машинной памяти или времени или алгоритмически проще, чем решение исходной системы.

Методом простой итерации называют явный метод с постоянм параметром

, или,

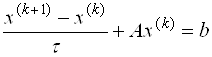
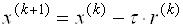
где r ( k ) = Ax ( k ) -b — вектор невязки. Метод сходится для симметричных положительно определенных матриц при .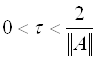

Для окончания итерационного процесса используют три способа. При первом определяют величину стабилизации и прекращают вычисления, если она меньше e, т.е.

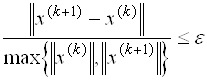
Недостатком этого способа является то, что при медленно сходящихся итерациях величина стабилизации может быть малой, хотя приближенное решение сильно отличается от точного.

При втором способе вычисляют нормы невязки до начала итераций и на каждой итерации. Итерации прекращают при выполнении неравенства

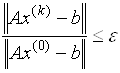
При третьем способе предварительно оценивается число итераций, необходимое для получения заданной точности e. Если для погрешности итерационного метода выполняются оценки

источники:

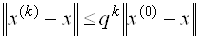
http://sopromat.in.ua/examples/nekotorye-varianty-resheniya-sistemy-uravnenii

http://kazedu.com/referat/133236

Решить систему уравнений в языке с

BestProg

Разработка приложения решения системы линейных алгебраических уравнений методом Гаусса

Условие задачи

Выполнение

Рубрики

Свежие записи

Сопромат .in.ua

Некоторые варианты решения системы уравнений

Решение online

Решение системы линейных алгебраических уравнений в OpenOffice.org

Пример решения системы линейных уравнений в Scilab

Пример

Пример решения системы линейных уравнений в среде программирования R

Пример

Решение системы линейных уравнений Ax=b в Euler Math Toolbox

Пример

Решение системы линейных уравнений