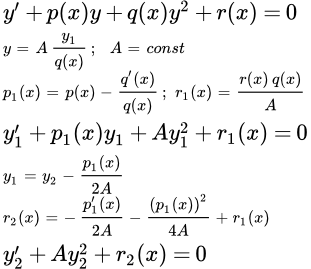Решить специальное уравнение риккати заменой переменных

Дифференциальное уравнение Риккати

Общее решение этого уравнения можно получить только в некоторых частных случаях.

Решение дифференциального уравнения Риккати при известном частном решении

Рассмотрим дифференциальное уравнение Риккати:
(1) .
Пусть известно его частное решение :

Тогда подстановкой уравнение Риккати (1) приводится к уравнению Бернулли:
;
;
;
;
.
Это уравнение Бернулли с n = 2 .

Свойства уравнения Риккати

Не меняет вид уравнения:

• Произвольное преобразование независимого переменного:
• Произвольное дробно-линейное преобразование зависимого переменного:

При таких подстановках уравнение также является уравнением Риккати, но с другими функциями p, q, r.

Вид общего решения

Общее решение уравнения Риккати есть дробно-линейная функция от произвольной постоянной:

И наоборот если общее решение уравнения есть дробно-линейная функция от произвольной постоянной, то соответствующее уравнение есть уравнение Риккати.

Упрощение уравнения Риккати

Снова рассмотрим дифференциальное уравнение Риккати:
(1) .
Подстановкой
,
где А – постоянная, оно приводится к виду:
(2) ,
где .

Далее, подстановкой

оно приводится к виду:
(3)
где .

Упрощенное уравнение Риккати

Упрощенное уравнение Риккати – это уравнение вида:
(4) ,
где A, B – постоянные. Оно интегрируется при
,
где – целое.

Покажем это. Сделаем подстановку:
;
.
Подставляем в (4):
.
Умножаем на :
(5) .
Но
.
Подставляем в (5):

Или
(6)
где
.
Уравнение (6) интегрируется при
.
Для этого разделим его на и перепишем в следующем виде:
;
;
.
Это уравнение с разделяющимися переменными. Оно легко интегрируется.

При уравнение (6) можно преобразовать двумя путями.

1. Подстановкой , где , оно преобразуется к виду: .
2. Подстановкой , где , оно преобразуется к виду:

Таким образом, при , где n — целое число, ряд подстановок приводит к полному решению.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 14-08-2012

Дифференциальное уравнение Риккати

Дифференциальное уравнение первого порядка вида

где — известные функции, называется уравнением Риккати (обобщенным). Если коэффициенты в уравнении Риккати постоянны, то уравнение допускает разделение переменных, и мы сразу получаем общий интеграл

Как показал Лиувилль, уравнение (1) в общем случае не интегрируется в квадратурах.

Свойства уравнения Риккати

1. Если известно какое-нибудь частное решение уравнения (1), то его общее решение может быть получено при помощи квадратур.

В самом деле, положим

где — новая неизвестная функция. Подставляя (2) в (1), найдем

откуда, в силу того что есть решение уравнения (1) получим

Уравнение (3) является частным случаем уравнения Бернулли.

Пример 1. Решить уравнение Риккати

зная его частное решение .

Решение. Положим и подставим в уравнение (4); получим

Таким образом, общее решение уравнения (4) .

Замечание. Вместо подстановки (2) часто бывает практически более выгодной подстановка

которая сразу приводит уравнение Риккати (1) к линейному .

2. Если известны два частных решения уравнения (1), то его общий интеграл находится одной квадратурой.

Пусть известны два частных решения и уравнения (1). Используя тот факт, что имеет место тождество

представим уравнение (1) в виде

Для второго частного решения аналогично находим

Вычитая из равенства (5) равенство (6), получаем

Пример 2. Уравнение имеет частные решения . Найти его общий интеграл.

Решение. Используя формулу (7), получаем общий интеграл исходного уравнения

Способ решения уравнения Риккати и линейные уравнения второго порядка Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Чочиев Тимофей Захарович

Более коротким и доступным путем изучается уравнение Риккати. Устанавливается решение . В данном варианте замечательны доказательства трех тождеств . Решается специальное уравнение Риккати. Решается линейное уравнение второго порядка.

Похожие темы научных работ по математике , автор научной работы — Чочиев Тимофей Захарович

Текст научной работы на тему «Способ решения уравнения Риккати и линейные уравнения второго порядка»

данный момент ситуацию, но и проанализировать, насколько успешны будут будущие проекты инвестирования в НИОКР.

Список использованной литературы

3. Knott A.M., Vieregger C., IQ and the R&D Market Value Puzzle // Management Science, 54. 2011. P. 2067.

Более коротким и доступным путем изучается уравнение Риккати. Устанавливается решение. В данном варианте замечательны доказательства трех тождеств. Решается специальное уравнение Риккати. Решается линейное уравнение второго порядка.

дифференциальное уравнение, решение, выполнимость, линейность, понижение порядка, переменность

коэффициентов, класс Риккати, тождества.

П.1. О тождествах уравнения Риккати.

В работе [2. 394 — 403; 3. 224 — 234] подробно было изучено уравнение Риккати. Установлено условие, выполнимость которого гарантирует решение в квадратурах. Доказывается выполнимость условия. В настоящем продолжаем изучать то же уравнение, но в другом варианте, с решением которого связаны три тождества [4.10 — 12].

Упомянутое уравнение в общей форме дается [1. с. 468]:

где I — искомая функция, А, В, и C заданные непрерывно дифференцируемые функции. (1.1.1) допускает ещё представление вида

©Иванова М.К., 2015

Чочиев Тимофей Захарович

Кандидат физико — математических наук, старший научный сотрудник ЮМИ ВНЦ РАН и РСО — А.

г. Владикавказ, РФ E — mail: madina-rso@yandex.ru

СПОСОБ РЕШЕНИЯ УРАВНЕНИЯ РИККАТИ И ЛИНЕИНЫЕ УРАВНЕНИЯ ВТОРОГО

Г + А(х)/2 + В(х)/ + ад = 0 ,

где Л-! и Я2 корни квадратного трёхчлена (1.1.1). Пусть I даётся формулой

-¡¿(АЛ^юах ll0 + J (АЛ1 — h)Aiefo(AÄi-h)dxdx

-f*(AX2-h)dx ll0 + J(AÄ2 — h)Ä2efo(AÄ2-h)dxdx

A* — A(Ä1 + Ä2) — ^ B* — -A2Ä1Ä2 — A(Ä1 + A2)’.

где 10 — постоянная, а к(х) решение нелинейного уравнения

к’ — к2 +А*к + В* = 0, (1.1.4)

Справедлива следующая теорема.

Теорема 1: Если в равенстве (1.1.2) 1(х) определяется формулой (1.1.3), к(х) удовлетворяет уравнению (1.1.4), то имеет место тождественная выполнимость равенств:

— е-!(AÄ2-h)dx (lo + |(AÄ2 — h)Ä2ef(AÄ2-h)dxdx )

2) I’ + A(l — Ä1)(l — Ä2) — 0,

3) AI + h — A(Ä1 + Ä2).

1) Первое равенство (1.1.5) переписывается

l0 +I(АЛ1 — h)Ä1e^0>(AXi-h->dxdx 0

— lo + IШ2 — h)Ä2e$°(AÄ2-h)dxdx,

или, дифференцируя, а потом сгруппировав, получим:

l0 + I (AÄ2 — h)A2e£(AX2-h)dxdx

= [—А(Х2 — Л2) + к(Л1 — Л2)]е£(А(Л2-,г)а^х.

Или, сократив на Л1 — Л2 и ещё раз продифференцировав,

-[к — А&1 + Л2)] — АШ2 — к)Л2 = = [к — А(Л1 + Л2)]’ + (АЛ2 — к)[к — А(Л1 + Л2)].

Отсюда после группировки следует:

h — А2Л1Л2 — А(Л1 + Л2)’ — 0.

Но последнее есть уравнение (1.1.4), которое по условию удовлетворяет. 2) Второе равенство (1.1.5) умножим на (Л1 — Л2),

(Л1 — Л2)1′ = —А(Л1 — Л2)(1 — Л1)(1 — Л2) и снова его переписываем в равносильной форме

II’ — II’ + (Л1 — Л2)1′ = —А(Л1 — Л2)(1 — Л1)(1 — Л2) ^

^ 1′(1 — Л2) — 1′(1 — Л1) = —А&1 — Л2)(1 — Л1)(1 — Л2) Очевидно, последнее есть уравнение (1.1.2). С другой стороны, из (1.1.3) следует:

Отсюда замечая, что

С4Я2 — Л)/ + (АЯ2 — Л)Я2 = -(ЛЯ2 — Л)(/ — Я2) Я = Я2.

га — Я2) — -(ЛЯ1 — л)(/ — Я1)(/ — Я2) i’d — Я1) — -Ш2 — л)(/ — Я2)(/ — Я1)

и подставляя значения в левую часть (1.1.6) получим:

—(ЛЯ! — к)(/ — яоа — Я2) + (^ — к)(/ — Л2)(/ — ЯО = = —л (Яг — Л2)(/ — Яг)(/ — Я2),

или, сокращая на — Яг)(/ — Я2), придём к тождеству

ЖЯ1 — Я2) = — ЖЯ1— Я2). То есть, если к(х) удовлетворяет уравнению (1.1.4), то (1.1.3) является решением уравнения (1.1.2), или уравнения (1.1.1).

3) В третьем равенстве выражения (1.1.5),

вместо / подставим одно из значений выражения (1.1.3) (пусть будет случай, когда Я = Я2,) будем иметь:

( Z0 + /(ЛЯ2 — Л)Я2е-Оя2-Л)^х ) — л(Я1 + Я2) — Л,

/0 + / (ЛЯ2 — Л)Я2е.оХ(лЯ2-h)dxdx — (я1 + Я2 — Л)

Отсюда после дифференцирования,

(яг + Я2 — к) + (ЛЯ2 — к) (яг + Я2 — к) = (ЛЯ2 — к)Я2, и приведя подобные члены получим уравнение,

Л — Л2Я1Я2 — Л(Я1 + Я2)’ — 0,

совпадающее с (1.1.4) и которое удовлетворяет. Что и требовалась.

Итак, если I дается формулой (1.1.3), к(х)-решение уравнения (1.1.4), то (1.1.3) удовлетворяет уравнению (1.1.2), или (1.1.6);тождественно выполняются первое и третье равенства выражения (1.1.5).

Таким образом, остается установить выполнимость уравнения (1.1.4), допускающее представление

П. 2. Решении уравнения (1.1.9).

Решение уравнения (1.1.9) будем искать в виде

/Очл^о)^ ( С1(х) — / (Я* + Л0)Я*1е-.оХ(я1+ло)й^ dx ), д — Я1,

где С1(х) и С2(х) — искомые функции, а к0 — неизвестная постоянная. Из (1.2.1) следует:

(Я1 + Л0)(Л(х) — Я*) + С1(х)е.оХ(я1+ло)^^ , (Я2 + Л0)(Л(Х) -Я2) + C2(x)e№+^ .

— -i* + hn | №) c(*rn+hnux 2* — л1 + h0 + h — 21 e 0

_h_ — X*+hn + C2(x) eS№+ho)d*

_ 2* — л2 + h0 + h — X*2e 0

С другой стороны, уравнение (1.1.9) допускает себя переписать

или, сгруппировав левую часть,

hh’ — hh’ + (А2* — A*2)h’ — (А\ — A*2)(h — A*)(h — Ä*2) ,

(h — A*2)h’ — (h — A\)h’ — (A\ — A*2)(h — A\)(h — A*2) ,

и разделив обе части на (к — А1)(к — А2) получим равносильное (1.1.9) соотношение

которое с учетом (1.2.2), переписывается

С1(х) c(*m+hn)dx — ^2 h — AI

С1(Х^> — JÜVdx . h — AI ‘

Или с учётом (1.2.1)

Отсюда следуют дифференциальные равенства

Н2(х) — —e^ridx Следовательно,

Я* + е£(Г1+>г0их j (Г* + hQ)Ale-£(ri+h°)dxdx 0

,2 + ei:(‘2+ho^»j(r2 + ho)r2e-i:»2+ho^»äX

— ef*efo^2+^dx ^ + j H1(x)e-foX^foX(Äl+Ä2+ho)dXdxdxj,

— efoxefo(^2+bo)dxdx I + fH2(x)e-foX^foX(Äl+Ä2+ho)dxäxdx),

удовлетворяют соответственно уравнениям (1.2.5), или (1.2. 4)’. Но тогда (1.2.4), или равенство (1.2.3), согласно (1.2.2)’ также удовлетворяет тождественно; то есть, (1.1.9) выполняется тождественно. Этим теорема 1 доказана.

Таким образом, функция к(х), определенная формулой (1.2.1), где Сг(х) и С2(х) выражаются соответственно через (1.2.6), удовлетворяет уравнению (1.2.3), или уравнению (1.1.9); функция 1(х), определенная через (1.1.3), удовлетворяет уравнению (1.1.6), или что тоже самое, уравнению (1.1.2), установлена тождественная выполнимость соотношений (1.1.5).

Нужно ещё уточнить к0 входящей в (1.2.1) и неизвестных постоянных у0 и (см. (1.1.3) и (1.2.6)), нахождение которых связано со значением функции к(х) и /(х) в нулевой точке.

Согласно (1.2.5) и (1.2.6)

ГС1(0) — С1(0) 1с2(0) — С2(0)

Я1(0) —/0-Я1(0) , Я2(0) — 70-^2(0) .

С другой стороны из (1.2.2) в нулевой точке имеем (см. (1.2.7)),

[Я1(0) + Ло][Л(0) — Я1(0)] + Го — Я*(0) , [Я2 (0) + Ло] [Л(0) — Я2 (0)] + Го — ¿2 (0) .

Поскольку к(0) — неизвестна, то её будем искать совпадением значений к'(0) в нулевой точке [Я*(0) + к0][к(0) — Я*(0)] +70 — Я!(0) = = [Я2(0) + к0][к(0) — Я2(0)] +70 — Я2(0)

[Я!(0) — Я2(0)]к(0) — я*2(0) + Я22(0) — ^(¿1(0) — Я2(0)> =

— я*(0) — Я2(0) ^ л(0) — л0 — 1 + Я1(0) + Я2(0).

Считая, что к0 = —к(0) для к(0) будем иметь:

Третье тождество выражения (1.5) дает:

к(0) =Л(0)[Яг(0)+Я2(0) — /(0)] . Отсюда и из (2.7)х для /(0) (/0 = /(0)) устанавливаем:

На основании (1.2.7) и (1.2.1)

Таким образом, располагая значениями постоянных (1.2.8), (1.2.9), функции /(х) и к(х), выраженные соответственно формулами (1.1.3) и (1.2.1) и удовлетворяющие (1.1.2) и (1.1.9), стали вполне определенными.

§2. О решении специального уравнения Риккати.

Известным, распространенным частным случаем уравнения Риккати считается пример Риккати,

где а,Ь и а — постоянные числа. Его называют специальным уравнениям Риккати [2.1]. (2.1.1) запишем