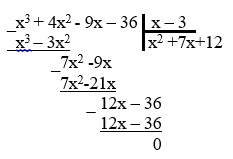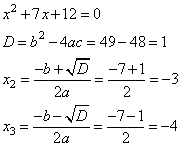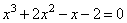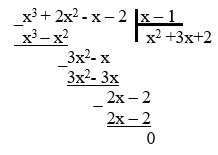Решение №886 Решите уравнение x^6 = – (12 – 8x)^3
Решите уравнение x 6 = – (12 – 8x) 3
x 6 = – (12 – 8x) 3
x 6 = x 2·3 = (x 2 ) 3 | –a 3 = (–a) 3
(x 2 ) 3 = (– (12 – 8x)) 3
a 3 = b 3
a = b
x 2 = – (12 – 8x)
x 2 = – 12 + 8x
x 2 – 8x + 12 = 0
D = (–8) 2 – 4·1·12 = 64 – 48 = 16 = 4 2
Ответ: 2; 6.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.5 / 5. Количество оценок: 54
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
«Решение уравнений высших степеней». 9-й класс
Разделы: Математика
Класс: 9
Учебная:
Развивающая:
- Развитие внимания учащихся.
- Развитие умения добиваться результатов труда.
- Развитие интереса к изучению алгебры и навыков самостоятельной работы.
Воспитывающая:
Оборудование: компьютер, проектор.
1 этап работы. Организационный момент.
2 этап работы. Мотивация и выход на постановку проблемы
Уравнение 
В школьном курсе изучения математики очень много внимания уделяется решению различного вида уравнений. До девятого класса мы умели решать только линейные и квадратные уравнения. Уравнения третьей, четвёртой и т.д. степеней называются уравнениями высших степеней. В девятом классе мы познакомились с двумя основными приёмами решения некоторых уравнений третьей и четвёртой степеней: разложение многочлена на множители и использование замены переменной.
А можно ли решить уравнения более высоких степеней? На этот вопрос мы постараемся сегодня найти ответ.
3 этап работы. Повторить ранее изученный материал. Ввести понятие уравнения высших степеней.
1) Решение линейного уравнения.
Линейным называется уравнение вида 


2) Решение квадратного уравнения.
Квадратным называется уравнение вида 







Из рассмотренных линейных и квадратных уравнений видим, что количество корней уравнения не более его степени. В курсе высшей алгебры доказывается, что уравнение 

Будем называть уравнения третьей, четвёртой и т.д. степеней уравнениями высших степеней. Некоторые уравнения высоких степеней удаётся решить с помощью двух основных приёмов: разложением многочлена 
3) Решение кубического уравнения.
Решим кубическое уравнение
Сгруппируем члены многочлена, стоящего в левой части уравнения, и разложим на множители. Получим:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три линейных уравнения:
Итак, данное кубическое уравнение имеет три корня: 


4) Решение биквадратного уравнения.
Очень распространены биквадратные уравнения, которые имеют вид 


Решим биквадратное уравнение 
Введём новую переменную 


Вернёмся к старой переменной 






Итак, данное биквадратное уравнение имеет четыре корня:



Попробуем решить уравнение 
4 этап работы. Привести некоторые утверждения о корнях многочлена вида 

Приведём некоторые утверждения о корнях многочлена вида 
1) Многочлен 


2) Многочлен нечётной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т.д. степени имеют хотя бы один корень. Многочлены чётной степени корней могут и не иметь.
3) Если на концах отрезка 


4) Если число 








5) Если уравнение 



5 этап работы. Показать как применяется теория делимости для решения уравнений высших степеней. Рассмотреть примеры решения уравнений высших степеней , в которых для разложения левой части на множители используется способ деления многочлена на многочлен “уголком”.
Пример 1. Решим уравнение 
Если это уравнение имеет целый корень, то он является делителем свободного члена (-1), т.е. равняется одному из чисел: 




Таким образом, мы фактически разложили левую часть уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:
Итак, данное уравнение имеет три корня:
Пример 2. Решим уравнение 
Если это уравнение имеет целый корень, то он является делителем свободного члена (9),т.е. равняется одному из чисел: 

Значит, многочлен 



Таким образом, мы разложили левую часть уравнения на множители:
Аналогичным образом поступим и с многочленом 
Если это уравнение 


Значит, многочлен 
произведения 


Таким образом, мы разложили левую часть исходного уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три уравнения:
Итак, данное уравнение имеет четыре корня:
6 этап работы. Закрепление изученного материала.
Решите уравнения высших степеней, используя способ деления многочлена на многочлен “уголком”.
7 этап работы. Вывод урока.
Решить уравнения высших степеней можно следующим образом:
- используя формулы для нахождения корней (если они известны);
- используя замену переменной;
- раскладывая многочлен в левой части уравнения на множители, используя способ деления многочлена на многочлен “уголком”.
8 этап работы. Домашнее задание.
Дома решить уравнения высших степеней, используя способ деления многочлена на многочлен “уголком” (раздать листы с заданиями).
Задание №21 ОГЭ по математике
Решение уравнений
В данном задании необходимо решить уравнение степени больше двух — это может быть биквадратное или кубическое уравнение. Ниже мы приводим алгоритмы решения типовых заданий!
Разбор типовых вариантов задания №21 ОГЭ по математике
Демонстрационный вариант ОГЭ 2019
Алгоритм решения:
- Определить тип уравнения.
- Перенести правую часть уравнения в левую.
- Привести уравнение к виду, при котором можно его многочлен слева разложить на множители.
- Разложить на множители.
- Приравнять каждый множитель к нулю
- Решить полученные уравнения.
- Записать ответ.
Решение:
1. Уравнение четвертой степени.
2. Перенесем правую часть уравнения в левую:
x 4 — (4x — 5) 2 = 0
3. Уравнение уже приведено к виду, при котором можно его левую часть разложить на множители.
4. Данное уравнение разложим на множители по формуле разности квадратов. Получим:
(х 2 – (4х-5))( х 2 + (4х-5)) = 0, или (х 2 – 4х+5)(х 2 + 4х-5) = 0.
5. Приравняем каждый множитель к нулю:
х 2 – 4х+5 = 0 и х 2 + 4х-5 = 0
6. Решим каждое из уравнений по формулам дискриминанта и корней:
Для первого уравнения:
D = b 2 -4ac = 16-20 = — 4, это означает, что первое уравнение х 2 – 4х+5 = 0 не имеет корней.
Для второго уравнения:
Определим корни второго уравнения:
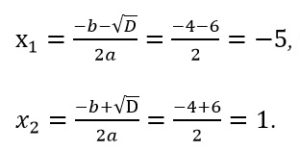
Первый вариант задания
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
Решение:
1. Перед нами уравнение третьей степени общего типа.
2. Найдем делители свободного члена данного уравнения. Это числа: 1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 12; -12;.18; -18; 36; -36.
3. Рассмотрим числа 1; -1; 2; -2; 3; -3. Это наименьшие среди найденных делителей. Подставим их по очереди в уравнение вместо х:
- для x=1:
— не подходит;
- для x=-1:
— не подходит;
- для х=2: 2 3 +4∙2 2 -9∙2=8=16-18-36=-38≠0 — не подходит;
- для х=-2: (-2) 3 +4∙(-2) 2 -9∙(-2)-36=-8+16+18-36=-10≠0 – не подходит;
- для x=3:
— подходит.
Мы нашли один корень.
4. Теперь выполним деление кубического многочлена на x-3, воспользовавшись схемой Горнера, имеем:
| 1 | 4 | -9 | -36 | |
| 3 | 1 | 7 | 12 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
5. После деления получаем квадратный трехчлен:
Составим квадратное уравнение для вычисления оставшихся двух корней:
6. Решим его с помощью формул корней и дискриминанта
7. Получили три корня 3; -3; -4.
Второй вариант задания
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
— для x=1: 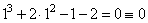
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
| 1 | 2 | -1 | -2 | |
| 1 | 1 | 3 | 2 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
5. Получаем квадратный трехчлен
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
http://urok.1sept.ru/articles/657320
http://ezmath.ru/ogje/zadanie-21/

















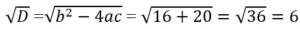
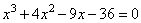
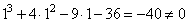 — не подходит;
— не подходит;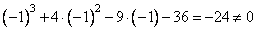 — не подходит;
— не подходит;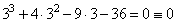 — подходит.
— подходит.