Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение показательных уравнений.
Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение
Немного теории.
Показательная функция, её свойства и график
Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m
4) (ab) n = a n b n
7) a n > 1, если a > 1, n > 0
8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \( a \neq 1\)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.
3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.
Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2
Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3 х = 7 х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac<3^x> <7^x>= 1 \), откуда \( \left( \frac<3> <7>\right) ^x = 1 \), х = 0
Ответ х = 0
Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t1 = 9, t2 = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2
Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
\( \left( \frac<2> <5>\right) ^
x — 2 = 0
Ответ х = 2
Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
5 класс. Математика. Виленкин. Учебник. Ответы к стр. 61
Ноя 19
5 класс. Математика. Виленкин. Учебник. Ответы к стр. 61
Натуральные числа
Сложение и вычитание натуральных чисел
Уравнение
Ответы к стр. 61
374. Составьте уравнение по рисунку 45 и решите его. 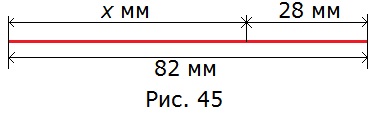
375. Решить уравнение (у + 64) — 38 = 48 можно двумя способами:
1) сначала найти неизвестное уменьшаемое у + 64:
у + 64 = 48 + 38, у + 64 = 86,
а потом найти неизвестное слагаемое у:
у = 86 — 64, у = 22 или
2) сначала упростить выражение, стоящее в левой части уравнения, использовав свойства вычитания:
у + 64 — 38 = 48, у + 26 = 48, а затем найти неизвестное слагаемое у:
у = 48 — 26, у = 22.
Подобным образом решите двумя способами уравнение:
а) (х + 98) + 14 = 169; б) (35 + у) — 15 = 31.
а) (х + 98) + 14 = 169, (х + 98) + 14 = 169,
х + 98 = 169 — 14, х + 98 + 14 = 169,
х + 98 = 155, х + 112 = 169,
х = 155 — 98, х = 169 — 112,
х = 57; х = 57;
б) (35 + у) — 15 = 31, (35 + у) — 15 = 31,
35 + у = 31 + 15, 35 + у — 15 = 31,
35 + у = 46, у + 20 = 31,
у = 46 — 35, у = 31 — 20,
у = 11; у= 11.
376. Решите уравнение и выполните проверку:
а) (х + 15) — 8 = 17; г) (у — 35) + 12 = 32;
б) (24 + х) — 21 = 10; д) 56 — (х + 12) = 24;
в) (45 — у) + 18 = 58; е) 55 — (х — 15) = 30.
а) (х + 15) — 8 = 17,
х + 15 = 17 + 8,
х + 15 = 25,
х = 25 — 15,
х = 10,
Проверка:
(10 + 15) — 8 = 17,
25 — 8 = 17,
17 = 17;
б) (24 + х) — 21 = 10,
24 + х = 10 + 21,
24 + х = 31,
х = 31 — 24,
х = 7,
Проверка:
(24 + 7) — 21 = 10,
31 — 21 = 10,
10 = 10;
в) (45 — у) + 18 = 58,
45 — у = 58 — 18,
45 — у = 40,
у = 45 — 40,
у = 5,
Проверка:
(45 — 5) + 18 = 58,
40 + 18 = 58,
58 =58;
г) (у — 35) + 12 = 32,
у — 35 = 32 — 12,
у — 35 = 20,
у = 20 + 35,
у = 55,
Проверка:
(55 — 35) + 12 = 32,
20 + 12 = 32,
32 = 32;
д) 56 — (х + 12) = 24,
56 — 24 = х + 12,
32 = х + 12,
х = 32 — 12,
х = 20,
Проверка:
56 — (20 + 12) = 24,
56 — 32 = 24,
24 = 24;
е) 55 — (х — 15) = 30,
55 — 30 = х — 15,
25 = х — 15,
х = 25 + 15,
х = 40,
Проверка:
55 — (40 — 15) = 30,
55 — 25 = 30,
30 = 30.
377. Решите с помощью уравнения задачу:
а) Витя задумал число. Если к этому числу прибавить 23 и к полученной сумме прибавить 18, то будет 52. Какое число задумал Витя?
б) Маша задумала число. Если к этому числу прибавить 14 и от полученной суммы отнять 12, то будет 75. Какое число задумала Маша?
в) В бензобак, где был бензин, перед поездкой долили ещё 39 л. Во время поездки израсходовали 43 л бензина, после чего в бензобаке осталось 27 л. Сколько литров бензина было в бензобаке первоначально?
г) В ателье было 60 м ткани. Из неё сшили платья, ещё 16 м израсходовали на детские костюмы, после чего осталось 20 м этой ткани. Сколько метров ткани пошло на платья?
Будем обозначать через х неизвестную величину.
а) (х + 23) + 18 = 52,
х + 23 = 52 — 18
х + 23 = 34,
х = 34 — 23,
х = 11.
О т в е т: задумано число 11.
б) (х + 14) — 12 = 75,
х + 14 = 75 + 12,
х + 14 = 87,
х = 87 — 14,
х = 73.
О т в е т: задумано число 73.
в) (х + 39) — 43 = 27,
х + 39 = 27 + 43,
х + 39 = 70,
х = 70 — 39,
х = 31.
О т в е т: был 31 л бензина.
г) (60 — х) — 16 = 20,
60 — х = 20 + 16,
60 — х = 36,
х = 60 — 36,
х = 24.
О т в е т: на платье пошло 24 м ткани.
ГДЗ учебник по математике 4 класс Петерсон. 21 урок. Движение по координатному лучу. Номер №9
Реши уравнения:
а) ( 300 * x − 72 ) : 7 = 96 + 108 ;
б) 200 − 560 : (y + 36 ) = 48 * 4 .
Решение а
( 300 * x − 72 ) : 7 = 96 + 108
( 300 * x − 72 ) : 7 = 204
300 * x − 72 = 204 * 7
300 * x − 72 = 1428
300 * x = 1428 + 72
300 * x = 1500
x = 1500 : 300
x = 5
Решение б
200 − 560 : (y + 36 ) = 48 * 4
200 − 560 : (y + 36 ) = 192
560 : (y + 36 ) = 200 − 192
560 : (y + 36 ) = 8
y + 36 = 560 : 8
y + 36 = 70
y = 70 − 36
y = 34
http://razviwaika.ru/5-klass-matematika-vilenkin-uchebnik-otvety-k-str-61/
http://reshalka.com/uchebniki/4-klass/matematika/peterson/706
