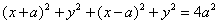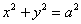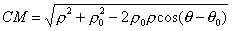Решить уравнение геометрического места точек

Решить уравнение геометрического места точек

Найти уравнение геометрического места точек, произведение расстояний которых до двух данных точек A и B есть величина постоянная, равная a 2 . Длину AB считать равной 2a.

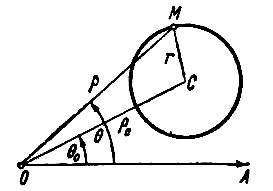
Проведем вывод уравнения в прямоугольных координатах. Направим ось Ox по прямой, соединяющей A и B, как обычно, вправо, начало координат поместим в середине отрезка AB, ось Oy направим вверх по перпендикуляру к оси Ox. Длина отрезка AB по условию равна 2a (AB = 2a); тогда точки A и B будут иметь координаты: A(-a, 0); B(a, 0). Пусть точка M принадлежит кривой. Ее координаты обозначим через x и y (см. рисунок).

Из условия задачи AM * BM = a 2 . По формуле расстояния между двумя точками

Возведем обе части этого уравнения в квадрат:

Решить уравнение геометрического места точек

Глава 10. Вывод уравнений заранее данных линий

В задачах предыдущего параграфа линия определялась при помощи данного уравнения. Здесь мы будем иметь задачи противоположного характера; в каждой из них линия определяется чисто геометрически, а уравнение ее требуется найти.

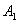
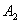
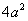
ПРИМЕР 1. В декартовой прямоугольной системе координат вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух данных точек (-а; 0) и (а; 0) есть величина постоянная, равная .

РЕШЕНИЕ. Обозначим буквой М произвольную точку линии, буквами х и у обозначим координаты этой точки. Так как точка М может занимать на линии любое положение то х и у являются переменными величинами; их называют текущими координатами.

Запишем геометрическое свойство линии символически:

(1).

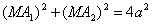
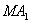
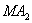
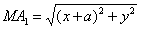
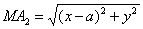
В этом отношении при движении точки М могут меняться длины и . Выразим их через текущие координаты точки М:

, (2)

Подставив полученные выражения в равенство (1), найдем уравнение, связывающее координаты х, у точки М:

Это и есть уравнение данной линии.

Действительно, для каждой точки М, лежающей на этой инии, выполняется условие (1) и, следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на линии, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).

Таким образом, задача решена. Однако уравнение (2) можно упростить; раскрывая скобки и приводя подобные члены, получим уравнение данной линии в виде:

Теперь легко понять, что данная линия есть окружность с центром в начале координат и радиусом, равным а.

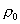
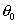
ПРИМЕР 2. В полярной системе координат вывести уравнение окружности, которая имеет центр С( ; ) и радиус r (см. рис.).

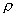
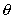
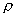
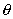
РЕШЕНИЕ. Олозначим буквой М произвольную точку окружности, буквами и — ее полярные координаты. Так как точка М может занимать на окружности любое положение, то и являются переменными величинами. Как и в случае декартовой системы, их называют текущими координатами.

Все точки окружности отстоят от центра на расстоянии r ; запишем это условие символически:

(1).

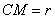
Выразим СМ через текущие координаты точки М (воспользуемся теоремой косинусов):

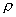
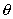
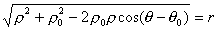
Подставив полученное выражение в равенство (1), найдем уравнение, связывающее координаты , точки М:

(2)

Это и есть уравнение данной окружности.

Действительно, для каждой точки М, лежащей на данной окружности, выполняется условие (1) и , следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на данной окружности, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).

Таким образом, задача решена. Можно лишь несколько упростить полученное уравнение и представить его в виде, свободным от радикала:

.

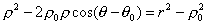
Составить уравнение геометрического места точек одинаково удаленных

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему нахождения геометрического места точек (ГМТ) по определенным условиям: удаленности от начала координат или произвольных точек, удаленности от кривых и прямых и т.п.

Геометрическое место точек: решения онлайн

Задача 1. Написать уравнение геометрического места точек, удаленных от прямой $х + 2у – 5 = 0$ на расстояние $sqrt $.

Задача 2. Составить уравнение линии, расстояние каждой точки которой от начала координат и от точки $(5;0)$ относятся как $2:1$.

Задача 3. Составить уравнение множества точек, для каждой из которых выполняется следующее условие: квадрат расстояния до точки $A(2,0)$ на 16 больше квадрата расстояния до оси ординат.

Задача 4. Составить уравнение линии, для каждой точки которой расстояние от точки $A(0,1)$ вдвое меньше расстояния от прямой $y=4$.

Задача 5. Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек $A(-3,0)$ и $B(0,3)$ равна 26. Построить эту линию.

Задача 6. Составить уравнение геометрического места точек, отношение расстояний которых до данной точки $A(2;0)$ и до данной прямой $x=4,5$ равно числу $2/3$. Полученное уравнение привести к простейшему виду и затем построить кривую.

Составить каноническое уравнение параболы, вершина которой лежит в начале координат и которая проходит через точку F(2;-4); ox– ось симметрии.

Ответ: .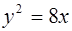

Задача 67.

Составить уравнение геометрического места точек, одинаково удаленных от точки F(2;0) и от прямой .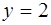

Ответ: .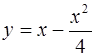

Задача 68.

Составить каноническое уравнение параболы, если ее фокус находится в точке пересечения прямой 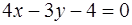с осью 0х.

Ответ: .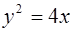

Задача 69.

На параболе 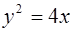найти точку, фокальный радиус которой равен 4.

Ответ: , .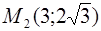

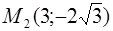
Задача 70.

Написать уравнение окружности, проходящей через начало координат и точки пересечения параболы 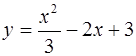с осями координат.

Ответ: .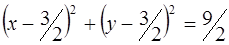

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8921 – | 7229 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Составить уравнение геометрического места точек, одинаково удаленных от точки F(0,2) и от прямой y=4. Найти точки пересечения этой кривой с осями координат и построить её

задан 23 Дек ’13 19:51

Надо приравнять квадраты расстояний от точки то точки, то есть $%x^2+(y-2)^2$%, и от точки до прямой, то есть $%(y-4)^2$%. После упрощений получится уравнение параболы. Остальное просто.

Здравствуйте

Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.