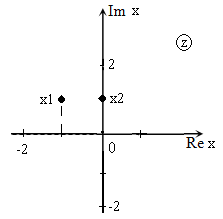Решить уравнение изобразить его корни

Решить уравнение изобразить его корни

. Вы вводите его по ссылке решение уравнений онлайн , указываете, что i — это комплексная единица (после того как ввели уравнение и нажали кнопку «решить»), нажимаете кнопку под формой «Обновить» и получаете ответ как здесь. Если в ответе присутствуют корни из комплексных чисел, то можно воспользоваться калькулятором по упрощению комлексных чисел по ссылке

© Контрольная работа РУ — примеры решения задач

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ <3>=8$.

Так как $A>0$, то $x_ =\sqrt[<3>] <8>\cdot \left(\cos \frac<2k\pi > <3>+i\cdot \sin \frac<2k\pi > <3>\right),\, \, \, k=0. 2$.

При $k=0$ получаем $x_ <0>=\sqrt[<3>] <8>\cdot \left(\cos 0+i\cdot \sin 0\right)=\sqrt[<3>] <8>=2$.

При $k=1$ получаем

\[x_ <1>=\sqrt[<3>] <8>\cdot \left(\cos \frac<2\pi > <3>+i\cdot \sin \frac<2\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>+\frac <\sqrt<3>> <2>\cdot i)=-1+\sqrt <3>\cdot i.\]

При $k=2$ получаем

\[x_ <2>=\sqrt[<3>] <8>\cdot \left(\cos \frac<4\pi > <3>+i\cdot \sin \frac<4\pi > <3>\right)=\sqrt[<3>] <8>\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=2\cdot (-\frac<1> <2>-\frac <\sqrt<3>> <2>\cdot i)=-1-\sqrt <3>\cdot i.\]

Решить уравнение: $x^ <3>=1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

\[\varphi =\arg z=arctg\frac<1> <1>=arctg1=\frac<\pi > <4>\]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ <0>=\sqrt[<3>] <\sqrt<2>> \cdot \left(\cos \frac<\pi /4> <3>+i\cdot \sin \frac<\pi /4> <3>\right)=\sqrt[<3>] <\sqrt<2>> \cdot \left(\cos \frac<\pi > <12>+i\cdot \sin \frac<\pi > <12>\right)=\sqrt[<6>] <2>\cdot \left(\cos \frac<\pi > <12>+i\cdot \sin \frac<\pi > <12>\right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

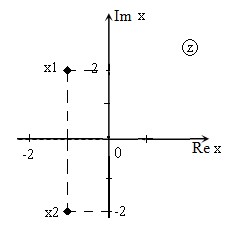
Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.

\[D=2^ <2>-4\cdot 1\cdot 5=4-20=-16.\]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $\overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.

Зная корни уравнения $x_ <1,2>=1\pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

\[x^ <2>-(1-2i)\cdot x-x\cdot (1+2i)+(1-2i)\cdot (1+2i)=0\] \[x^ <2>-x+2i\cdot x-x-2i\cdot x+1-4i^ <2>=0\] \[x^ <2>-2x+1+4=0\] \[x^ <2>-2x+5=0\]

Следовательно, $x^ <2>-2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ <2>+(1-2i)\cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 11 2021

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Работаем по будням с 10:00 до 20:00 по Мск

. и многие другие.
Успешной учебы! Будем рады вам помочь!

Урок по теме «Решение уравнений с модулем, используя его геометрический смысл». 9-й класс

Класс: 9

Ключевые слова: Решение уравнений с модулем

Цели урока:

• предметная:
  • формирование умения применять геометрическую интерпретацию модуля при решении линейных уравнений;
• метапредметные:
  • развивать умения анализировать, сравнивать, обобщать, делать выводы,
  • развитие информационной, коммуникативной, исследовательской компетентностей;
• личностные:
  • содействовать формированию личностно-адаптивной компетентности (быть подготовленным к самообразованию и самовоспитанию),
  • развивать внимание, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цели.

Тип урока: изучение нового материала.

Методы организации и осуществления учебной деятельности:

• по источникам знаний: практические;
• по характеру мыслительных операций: индуктивные;
• по степени взаимодействия учитель-ученик: исследование объектов изучения под руководством учителя;
• относительно дидактических задач: обобщение изученного;
• относительно характера познавательной деятельности: исследовательский;
• относительно стимулирования и мотивации учебной деятельности:
• стимулирование интересов к учению: опора на неожиданность, создание ситуации новизны;
• устные и письменные;
• групповые (работа в группах);
• технические (мультимедийная аппаратура).

Оборудование: мультимедийный комплекс, компьютер, задания для групп, геометрическая модель.

Структура урока.

1. Психологический настрой на деятельность. Мотивация учебной деятельности.
2. Изучение нового материала.
   1. учебное исследование;
   2. обсуждение итогов учебного исследования;
   3. схематизация материала.
3. Домашнее задание.
4. Рефлексия. Подведение итогов.

Ход урока

I. Психологический настрой на деятельность. Мотивация учебной деятельности

Слайд 1. Записываем дату и тему урока.

Слайд 2. Вспомним:

Модуль числа a равен a, если a больше или равно нулю и равен –a, если a меньше нуля.

Из определения следует, что для любого действительного числа a:

Слайд 3. Решаем устно:

2. | |

3. | |

4.

5.

6.

Слайд 4. Работа устно:

Сколько корней имеет данное уравнение? Найдите их.

II. Изучение нового материала

1. Объяснение нового материала

Эти уравнения можно решить другим способом, используя геометрический смысл модуля. Давайте дадим геометрическое истолкование модуля действительного числа а?

Слайд 5. Геометрический смысл модуля:

Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).

1. Модуль числа 5 равен 5. Пишут: |5| = 5.
2. Число 6 называют модулем числа -6. Пишут: |-6| = 6.
3. Модуль числа не может быть отрицательным.
4. Противоположные числа имеют равные модули:| -а | = | а |

1. Как изобразить на координатной прямой | 5 | и | -6 |?
   1. | 5 | – расстояние от начала координат О до точки В(5).
   2. | -6 | – расстояние от начала координат О до точки М(-6).
2. Почему модуль не может быть отрицательной величиной?
3. Почему противоположные числа имеют равные модули?

Слайд 6.

1. Как расположены на числовой прямой точки с координатами -4; -2; 1 и 5?
2. Как найти расстояние между точками на координатной прямой?

Слайд 7.

• Что называется расстоянием между двумя точками на координатной прямой?
• В чем состоит геометрический смысл модуля разности действительных чисел?

Слайд 8. Прочитать и объяснить словесную запись:

Записать аналитическую модель рисунка в тетради (рисунок на доске).

Слайд 9. |х-2|=3

Вопрос: в чем заключается смысл задания с геометрической точки зрения?

Ответ: Найти точки, которые находятся на расстоянии 3 ед. отрезков от точки 2 (изображаем на доске)

Вопрос: Прочитайте данное уравнение с помощью геометрического смысла модуля |х+5|=3, найдите его корни, используя координатную прямую.

Ответ: Найти точки, которые находятся на расстоянии 3 ед. отрезков от точки -5.

Корни уравнения: х=-2; х=-8.

Слайд 9. Решение уравнений с помощью геометрической интерпретации модуля:

Вопрос: Посмотрите внимательно на данное уравнение и попробуйте сами сформулировать задание с геометрической точки зрения

Ответ: Расстояние от х до -5 и 2 должно быть одинаковым.

Вопрос: Попробуйте составить план решения этого уравнения с помощью координатной прямой.

а) найдем расстояние между точками -5 и 2. 5+2=7.

б) т.к. х равноудалена от точек -5 и 2, найдем половину этого расстояния: 7/2=3,5

в) найдем координату точки: -5+3,5=-1,5 или 2-3,5=-1,5

Слайд 10. Вопрос: Как решить уравнение?

Ответ: Выражение |х-5| можно истолковать, как расстояние между точками с координатами х и 5.

Выражение |х+1| можно истолковать, как расстояние между точками с координатами х и -1.

Тогда уравнение означает, что нужно найти такую точку Х(х), сумма расстояний от которой до точек с координатами 5 и -1 равна 8.

Расстояние между точками с координатами 5 и -1 равно 6 23.11.2020