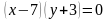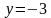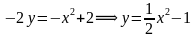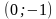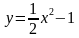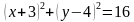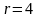Решить уравнение изобразить его корни на координатной плоскости

Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными

Примеры изображения на координатной плоскости множества решений уравнений, неравенств и систем неравенств с двумя переменными

Просмотр содержимого документа
«Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными»

Изображение на координатной плоскости множества решений уравнений и неравенств

с двумя переменными.

1. Изображение множества решений уравнений с двумя переменными.

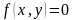
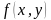
Определение. Уравнение вида , где — некоторая функция переменных х и у, называется неравенством с двумя неизвестными х и у.

Решить уравнение – значит найти множество всех его корней.

Решением уравнения с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное уравнение в верное числовое равенство.

Для того, чтобы решить уравнение с двумя переменными нужно построить его график.

Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.

Задача 1. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения

Так как произведение равно нулю, то каждый из множителей также равен нулю.

Решим каждое из полученных уравнений:

или

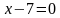
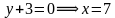
Решением является множество точек двух прямых: ,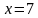

Задача 2. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения .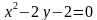

Для этого выразим переменную .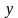

Уравнение задает параболу с вершиной в точке

То есть решением уравнения является множество точек параболы

Задача 3. Изобразить на координатной плоскости множество решений уравнений

Построим график уравнения

Уравнение задает окружность с центром в точке 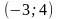, радиусом

То есть решением уравнения является множество точек построенной окружности

2. Изображение множества решений неравенств с двумя переменными.

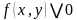
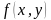
Определение. Выражение вида , где — некоторая функция переменных х и у, называется неравенством с двумя неизвестными х и у.

Решить неравенство – значит найти множество всех его решений.

Решением неравенства с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное неравенство с переменными в верное числовое неравенство.

Алгоритм решения неравенства

1. Построить график уравнения .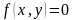

Если неравенство «строгое», тогда график изображаем пунктирной линией;

Если неравенство «нестрогое», тогда график изображаем сплошной линией.

2. Выделить штриховой часть координатной плоскости, соответствующей знаку неравенства.

Задача 1. Изобразить на координатной плоскости множество решений неравенства

Построим график заданного неравенства . Для этого выразим переменную .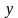

Уравнение задает линейную функцию, проходящую через точки:

Поскольку неравенство имеет знак «больше либо равно», значит выделяем часть координатной плоскости, которая лежит выше построенной прямой . Выделенная часть является решением заданного неравенства.

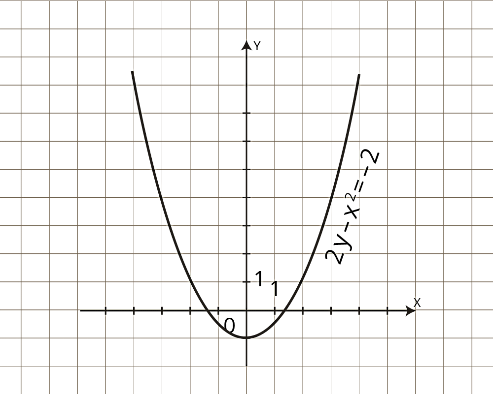
Задача 2. Изобразить на координатной плоскости множество решений неравенства

Построим график заданного неравенства.

Уравнение задает параболу с вершиной в точке

Поскольку заданное неравенство имеет знак «больше либо равно», значит решением неравенства является множество всех точек, расположенных выше (внутри) параболы.

Задача 3. Изобразить на координатной плоскости множество решений неравенства .

Графиком уравнения является гипербола .

Данная гипербола разбивает координатную плоскость на три области А, В и С.

Для определения необходимой области нужно выбрать контрольные точки, по одной из каждой области.

Возьмем из области А точку с координатами (5;4). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область А входит в решение заданного неравенства.

Возьмем из области В точку с координатами (1;2). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили неверное неравенство. Значит область В не входит в решение заданного неравенства.

Возьмем из области С точку с координатами Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область С входит в решение заданного неравенства.

3. Изображение множества решений системы неравенств с двумя переменными.

Решить систему неравенств – значит найти множество всех решений системы.

Решением системы неравенств с двумя переменными называется любая упорядоченная пара (х; у), которая обращает все неравенства заданной системы в верные числовые неравенства.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы

Задача 4. Изобразить на координатной плоскости множество решений системы неравенств

На координатной плоскости множество всех решений неравенства

изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой (смотри задачу 1).

Аналогично строим график неравенства .

То есть строим на координатной плоскости прямую

Множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.

Задача 5. Изобразить на координатной плоскости множество решений системы неравенств

На координатной плоскости множество всех решений неравенства

изображается в виде множества точек полуплоскости, лежащих ниже параболы и на этой параболе.

Аналогично, множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше параболы и на этой параболе.

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.

Извлечение корня из комплексного числа

Третий урок по комплексным числам. В этом уроке вы узнаете:

Начнём с ключевого определения.

1. Определение комплексного корня

Определение. Корнем $n$-й степени из комплексного числа $z$, где $n\in \mathbb$, $n \gt 1$, называется такое комплексное число $\omega $, что

т.е. $n$-я степень числа $\omega $ равна $z$.

Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:

Пример. Вычислить $\sqrt[3]<-1>$ на множестве комплексных чисел.

Очевидно, привычная нам единица является таким корнем, потому что $<<\left( -1 \right)>^<3>>=-1$. Но есть ещё два корня:

Итого три корня. Как и предполагалось.

Теорема. Для любого комплексного числа $z\ne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$

Все эти корни считаются по следующей формуле.

2. Формула корней

Теорема. Пусть комплексное число записано в тригонометрической форме:

\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]

Тогда все корни степени $n$ из этого числа можно найти по формуле:

По сути, эта теорема является обратной к формуле Муавра:

Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:

1. Перевести комплексное число в тригонометрическую форму;
2. Записать общую формулу корня степени $n$;
3. Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
4. Получим $n$ комплексных корней. Вместе они и будут ответом.

В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $z\ne 0$.

Представим число $-8i$ в тригонометрической форме:

\[\begin -8i &=0+\left( -8 \right)\cdot i= \\ & =8\cdot \left( 0+\left( -1 \right)\cdot i \right)= \\ & =8\cdot \left( \cos \left( -\frac<\pi > <2>\right)+i\sin \left( -\frac<\pi > <2>\right) \right) \end\]

Запишем формулу корней в общем виде:

\[\sqrt[3]<-8i>=2\cdot \left( \cos \left( -\frac<\pi > <6>\right)+i\sin \left( -\frac<\pi > <6>\right) \right)=\sqrt<3>-i\]

В ответе нужно указать все три числа: $-2i$; $\sqrt<3>-i$; $-\sqrt<3>-i$.

Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $\left\< 0,1. n-1 \right\>$, то корни начнут повторяться, и ничего нового мы не получим.

3. Геометрическая интерпретация

Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $z\ne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=\sqrt[n]<\left| z \right|>$. Более того: эти точки образуют правильный $n$-угольник.

Отметить на комплексной плоскости все числа вида $\sqrt[3]$.

Представим число $z=i$ в тригонометрической форме:

\[\begin z & =1\cdot \left( 0+i\cdot 1 \right)= \\ & =1\cdot \left( \cos \frac<\pi ><2>+i\sin \frac<\pi > <2>\right) \end\]

Формула комплексных корней:

\[\sqrt[3]=1\cdot \left( \cos \left( \frac<\pi ><6>+\frac<2\pi k> <3>\right)+i\sin \left( \frac<\pi ><6>+\frac<2\pi k> <3>\right) \right)\]

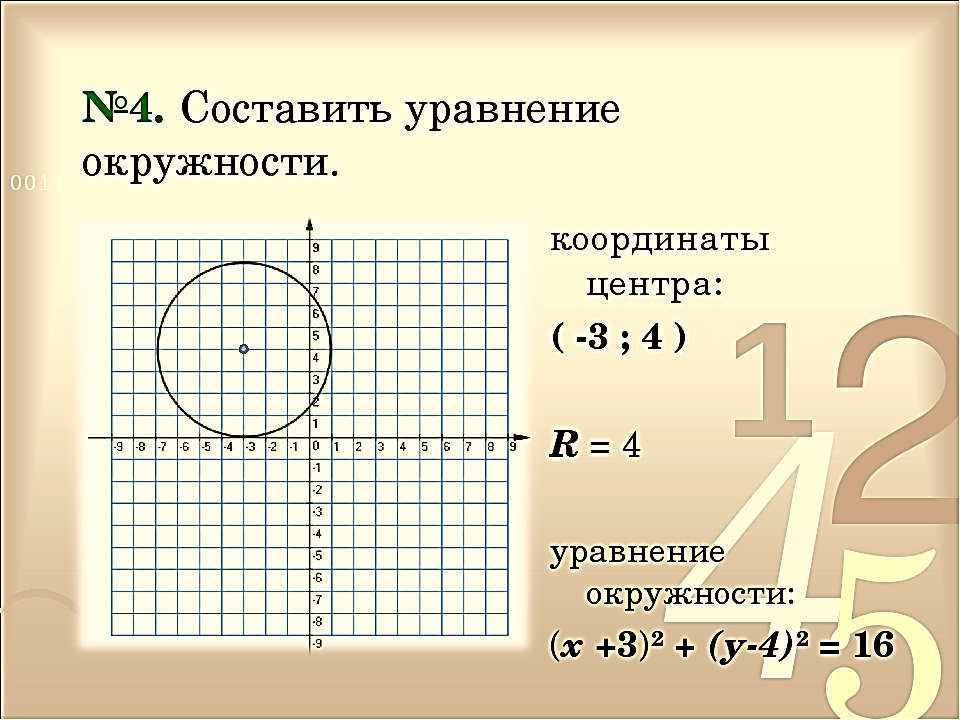
Это три точки $<_<1>>$, $<_<2>>$ и $<_<3>>$ на окружности радиуса $R=1$:

Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол $<\pi >/<6>\;$.

Рассмотрим более сложный пример:

Отметить на комплексной плоскости все числа вида $\sqrt[4]<1+i>$.

Сразу запишем формулу корней с выделением начального луча:

\[\sqrt[4]=\sqrt[8]<2>\cdot \left( \cos \left( \frac<\pi ><16>+\frac<\pi k> <2>\right)+i\sin \left( \frac<\pi ><16>+\frac<\pi k> <2>\right) \right)\]

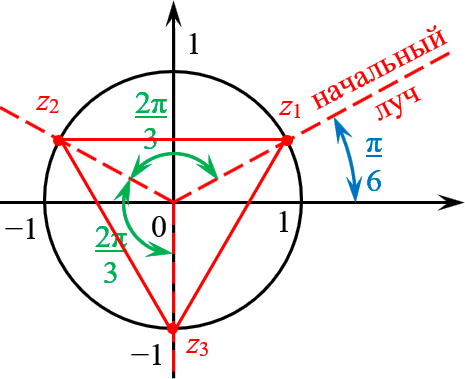
Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=\sqrt[8]<2>$, начальный луч $<\pi >/<16>\;$:

И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча $<\pi >/<16>\;$.

Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:

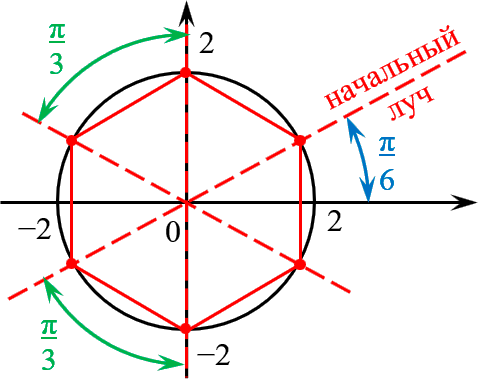
Отметить на комплексной плоскости все числа вида $\sqrt[6]<-64>$.

Формула корней с выделением начального луча:

\[\sqrt[6]=2\cdot \left( \cos \left( \frac<\pi ><6>+\frac<\pi k> <3>\right)+i\sin \left( \frac<\pi ><6>+\frac<\pi k> <3>\right) \right)\]

Получили правильный шестиугольник со стороной 2 и начальным лучом $<\pi >/<6>\;$.

Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $z\ne 0$:

1. Перевести число в тригонометрическую форму;
2. Найти модуль корня: $\sqrt[n]<\left| z \right|>$ — это будет радиусом окружности;
3. Построить начальный луч с отклонением $\varphi =<\arg \left( z \right)>/\;$;
4. Построить все остальные лучи с шагом $<2\pi >/\;$;
5. Получим точки пересечения лучей с окружностью — это и есть искомые корни.

Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $\varphi $ — стандартные «табличные» углы вроде $<\pi >/<6>\;$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)

4. Почему корней всегда ровно n

С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.

Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:

Последовательно подставим в эту формулу указанные значения параметра $k$:

Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:

Поскольку синус и косинус — периодические функции с периодом $2\pi $, $<<\omega >_>=<<\omega >_<0>>$, и далее корни будут повторяться. Как мы и заявляли в самом начале урока.

5. Выводы

Ключевые факты из урока.

Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $\omega $, что $<<\omega >^>=z$.

Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $\omega =\sqrt[n]$.

Замечание. Если $z\ne 0$, таких чисел корней будет ровно $n$ штук.

Алгоритм нахождения корней состоит из двух шагов.

Шаг 1. Представить исходное число в тригонометрической форме:

\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]

Шаг 2. Воспользоваться формулой Муавра для вычисления корней:

Все полученные корни лежат на окружности радиуса $\sqrt[n]<\left| z \right|>$ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол $<\varphi >/\;$. Остальные вершины обычно легко находятся из соображений симметрии с помощью циркуля и линейки.

Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».

Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)

Презентация к уроку по математике на тему «Решение квадратных уравнений с помощью комплексных чисел» 1 курс специальность «Мастер по лесному хозяйству»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Решение квадратных уравнений с помощью комплексных чисел

«Комплексное число – это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием». Г. Лейбниц

Термин “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века — Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа i(мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово «комплекс» (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. образующих единое целое.

Н. Н. Богомолов и В. С. Владимиров — к проблемам квантовой теории поля. Большой вклад в развитие теории функций комплексного переменного внесли русские и советские ученые: Н. И. Мусхелишвили занимался ее применениями к теории упругости; М. В. Келдыш и М. А. Лаврентьев — к аэро- и гидродинамике;

Обозначение: – алгебраическая форма записи комплексного числа Комплексным числом называется число вида a+ib , где a, b − некоторые действительные числа, а i− мнимая единица, при чем:

Множество комплексных чисел обозначается С, N Z Q I R C

Число a называется действительной частью комплексного числа z. Обозначается a=Re z. Число b называется мнимой частью комплексного числа z. Обозначается b=Im z.

Мнимая ось Действительная ось 0 1 1 a b M(a; b) z=a+jb

Примеры: 1) Изобразите комплексные числа

2) Запишите комплексные числа, изображенные на координатной плоскости, в алгебраической форме. 0 1 1 -2 4 3 2 -3 -4 -5

3) На какой из координатных плоскостей изображено число 0 1. 2. 3. 4. 0 0 0

Степени мнимой единицы По определению: Таким образом, можно вывести формулу для вычисления

Исследование алгебраических уравнений является одним из важнейших вопросов математики. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение x²+1=0 Для того чтобы это уравнение имело решение, необходимо расширить множество действительных чисел путем присоединения к нему корня уравнения x²=-1 Обозначим этот корень через i,тогда по определению i²+1=0 i²=-, а следовательно i=√-1

На множестве С можно находить корни любых квадратных уравнений! Как извлечь квадратный корень из отрицательных действительных чисел? Решение квадратных уравнений с действительными коэффициентами и D

Краткое описание документа:

Урок на тему: «Решение квадратных уравнений с помощью комплексных чисел».

Цели:

Образовательные: расширить понятие числа, ввести понятие комплексного числа, действия над комплексными числами, заданными в алгебраической форме.

Воспитательные: прививать интерес к математике, ознакомить учащихся с историей развития комплексных чисел, воспитывать

Развивающие: развивать творческое мышление, пространственное мышление, научить применять теоретические знания при решении практических задач, формировать активность и самостоятельность при работе в группах.

Используемые технологии и методы: 1) проблемный диалог; 2) информационно- коммуникационные технологии.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 920 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 685 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 582 839 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 11.08.2018
• 209
• 0

• 11.08.2018
• 366
• 2

• 11.08.2018
• 441
• 1

• 11.08.2018
• 1407
• 30

• 11.08.2018
• 355
• 0

• 11.08.2018
• 648
• 2

• 10.08.2018
• 913
• 25

• 10.08.2018
• 600
• 7

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 11.08.2018 1756
• PPTX 1.6 мбайт
• 74 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Ломова Людмила Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 14488
• Всего материалов: 21

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.