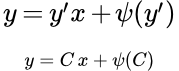Дифференциальное уравнение Клеро
Решение дифференциального уравнения Клеро
Рассмотрим уравнение Клеро:
(1)
Не трудно убедиться, что его общее решение имеет вид:
(2)
Действительно, поскольку – постоянная, то – тоже постоянная. Тогда дифференцируя (2) имеем:
;
(3) .
Подставляя (2) и (3) в (1), получаем тождество:
.
Особое решение дифференциального уравнения Клеро
Уравнение Клеро может иметь особое решение. Как известно, если общее решение дифференциального уравнения имеет вид:
,
то особое решение может получиться исключением из уравнений:
;
.
В нашем случае, решение (2) можно записать в виде:
.
Тогда
.
Тогда особое решение может получиться, исключением из уравнений:
;
.
Поскольку возможны посторонние решения, то после нахождения особого решения, необходимо проверить, удовлетворяет ли он исходному уравнению (1).
Пример
Решить уравнение:
(1.1)
Это уравнение Клеро. Его общее решение имеет вид:
Ищем особое решение. Перепишем общее решение в виде:
.
Дифференцируем по :
.
Тогда особое решение может получиться исключением из уравнений:
(1.2) ;
(1.3) .
Исключаем . Из уравнения (1.3) имеем:
(1.4) .
Возводим в квадрат и преобразуем:
;
;
. Отсюда следует, что .
Извлекаем квадратный корень:
(1.5) .
Поскольку мы возводили в квадрат, то, возможно, (1.5) содержит лишние решения, которые не удовлетворяют (1.4). Сейчас мы примем (1.5), а отсев лишних решений сделаем в самом конце.
Подставим (1.4) и (1.5) в (1.2):
.
Итак, особые решения имеют вид:
(1.6) .
Теперь сделаем проверку, чтобы выяснить, удовлетворяет ли исходному уравнению (1.1):
(1.1) .
Находим производную (1.6) и выполняем преобразования:
;
;
.
Подставляем в (1.1):
(1.7) .
При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять нижний знак:
.
То есть при , .
При , . Уравнение (1.7) принимает вид:
.
Оно выполняется, если взять верхний знак:
.
То есть при , .
Общее решение уравнения имеет вид:
При уравнение имеет особое решение:
.
При уравнение имеет особое решение:
.
Автор: Олег Одинцов . Опубликовано: 24-08-2012 Изменено: 10-04-2016
Уравнение Клеро
Вы будете перенаправлены на Автор24
Дифференциальные уравнения первого порядка, не разрешенные относительно производной.
В общем виде дифференциальные уравнения первого порядка, не разрешенные относительно производной, записываются как $F\left(x,y,y’\right)=0$.
Основной метод решения таких дифференциальных уравнений состоит в том, чтобы выполнить некоторые преобразования, приводящие к уравнениям, разрешенным относительно производной. В дальнейшем могут применяться любые из известных методов, соответствующие тому, что в результате получилось: или уравнение с разделяющимися переменными, или однородное уравнение, или линейное уравнение и т.п.
Решить дифференциальное уравнение $y’^ <3>-y’^ <2>\cdot x+2\cdot y’=2\cdot x$.
Данное дифференциальное уравнение не разрешено относительно производной, поэтому известные методы для его решения применить не удается.
Поэтому выполняем следующие преобразования:
- все слагаемые переносим в одну сторону $y’^ <3>-y’^ <2>\cdot x+2\cdot y’-2\cdot x=0$;
- выражение слева разлагаем на множители $\left(y’^ <2>+2\right)\cdot \left(y’-x\right)=0$;
- так как $y’^ <2>+2\ne 0$, то исходное уравнение эквивалентно $y’-x=0$.
Получено дифференциальное уравнение, допускающее непосредственное интегрирование: $\frac
Отсюда: $y=\int x\cdot dx $; $y=\frac
Решить дифференциальное уравнение
\[y’^ <2>-y’\cdot y+\cos x\cdot \left(y’-y\right)=0.\]
Данное дифференциальное уравнение не разрешено относительно производной, поэтому выполняем преобразования:
\[y’\cdot \left(y’-y\right)+\cos x\cdot \left(y’-y\right)=0;\] \[\left(y’-y\right)\cdot \left(y’+\cos x\right)=0.\]
Таким образом, данное дифференциальное уравнение эквивалентно двум другим: $y’-y=0$ и $y’+\cos x=0$.
Первое дифференциальное уравнение $y’-y=0$ решается посредством разделения переменных:
Второе дифференциальное уравнение $y’+\cos x=0$ допускает непосредственное интегрирование: $\frac
Метод введения параметра
В ряде случаев дифференциальное уравнение вида $F\left(x,y,y’\right)=0$ не удается разрешить относительно производной. Но вполне возможно, что оно разрешимо или относительно $y$, или относительно $x$. Тогда мы получаем дифференциальное уравнение общего вида $y=u\left(x,y’\right)$ или $x=v\left(y,y’\right)$. Некоторые из дифференциальных уравнений подобного вида можно решить методом введения параметра.
Рассмотрим пример дифференциального уравнения вида $x=f\left(y’\right)$.
Решается введением параметра $\frac
В результате имеем решение данного дифференциального уравнения в параметрической форме, задаваемое следующими выражениями:
Готовые работы на аналогичную тему
Решить дифференциальное уравнение $8\cdot y’^ <3>=27\cdot x$.
Здесь мы имеем дифференциальное уравнение вида $x=f\left(y’\right)$, не разрешенное относительно производной.
Вводим параметр $\frac
Здесь $f\left(p\right)=\frac<8> <27>\cdot p^ <3>$, откуда $\frac
Таким образом, решение данного дифференциального уравнения в параметрической форме задается следующими выражениями:
Отсюда получаем: $\left\<\begin
Параметр $p$ из этой системы уравнений можно исключить:
из $x=\frac<8> <27>\cdot p^ <3>$ получаем $p^ <3>=\frac<27> <8>\cdot x$ или $p=\frac<3> <2>\cdot x^<\frac<1> <3>> $;
подставляем в $y=\frac<2> <9>\cdot p^ <4>+C$ и получаем $y=\frac<2> <9>\cdot \left(\frac<3> <2>\cdot x^<\frac<1> <3>> \right)^ <4>+C$ или $y=\frac<9> <8>\cdot x^<\frac<4> <3>> +C$.
Таким образом, получено общее решение $y=\frac<9> <8>\cdot x^<\frac<4> <3>> +C$ данного дифференциального уравнения $8\cdot y’^ <3>=27\cdot x$ в явной форме.
Решение уравнения Клеро
Уравнение Клеро имеет вид $y=x\cdot y’+\psi \left(y’\right)$ и относится к более сложным видам дифференциальных уранений, не разрешенных относительно производной.
Введим параметр $\frac
После дифференцирования и простых преобразований получаем уравнение $\frac
Из этого уравнения следует $p=C$. Отсюда получаем общее решение дифференциального уравнения Клеро $y=x\cdot C+\psi \left(C\right)$. Иначе говоря, общее решение можно получить из данного уравнения $y=x\cdot y’+\psi \left(y’\right)$ формальной заменой $y’$ на $C$.
Уравнение $x+\psi ‘\left(p\right)=0$.
Это уравнение дает особое решение в параметрической форме:
Оно представляет собой огибающую семейства кривых общего решения.
Решить дифференциальное уравнение $y=x\cdot y’+y’$.
Имеем уравнение Клеро, в котором $\psi \left(y’\right)=y’$.
Вводим параметр $\frac
Формально заменив в данном дифференциальном уравнении $y’$ на $C$, получим его общее решение $y=x\cdot C+C$ или $y=C\cdot \left(x+1\right)$.
Находим особое решение.
Так как $\psi \left(p\right)=p$ и $\frac
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 19 01 2022
Дифференциальные уравнения 1-го порядка,
не разрешенные относительно производной
Уравнения 1-го порядка n-ой степени относительно производной
Пусть имеем дифференциальное уравнение
Решаем это уравнение относительно . Пусть
— вещественные решения уравнения (1).
Общий интеграл уравнения (1) выразится совокупностью интегралов:
где есть интеграл уравнения .
Таким образом, через каждую точку области, в которой принимает вещественные значения, проходит интегральных линий.
Пример 1. Решить уравнение .
Решение. Разрешим это уравнение относительно :
Пример 2. Решить уравнение .
Решение. Разрешим уравнение относительно переменной :
Положим , где — параметр; тогда получим Дифференцируя, найдем . Но так как , то будем иметь
Рассмотрим два случая:
1) , откуда , где — произвольная постоянная. Подставляя значение , получаем общее решение данного уравнения:
В равенстве нельзя заменить на и интегрировать полученное уравнение (так как при этом появится вторая произвольная постоянная, чего не может быть, поскольку рассматриваемое дифференциальное уравнение является уравнением первого порядка).
2) , откуда . Подставляя, получим еще одно решение .
Проверим, нарушится ли свойство единственности в каждой точке решения , т.е. является ли оно особым (см. часть 1.11). Для этого возьмем на интегральной кривой произвольную точку , где . Будем теперь искать решение, которое содержится в общем решении и график которого проходит через точку . Подставляя координаты этой точки в общее решение , будем иметь
откуда . Это значение постоянной подставим в . Тогда получим частное решение
которое не совпадает с решением . Для этих решений имеем соответственно . При обе производные совпадают. Следовательно, в точке нарушается свойство единственности, т. е. через эту точку проходят две интегральные кривые с одной и той же касательной. Так как произвольно, то единственность нарушается в каждой точке решения , а это означает, что оно является особым.
2°. Уравнения вида f(y,y’)=0 и f(x,y’)=0
Если уравнения и легко разрешимы относительно , то, разрешая их, получим уравнения с разделяющимися переменными. Рассмотрим случаи, когда эти уравнения не разрешимы относительно .
А. Уравнение вида разрешимо относительно :
Полагаем , тогда . Дифференцируя это уравнение и заменяя на , получим
Получаем общее решение уравнения в параметрической форме
Пример 3. Решить уравнение , где — постоянные.
Решение. Положим , тогда , или . Отсюда и .
Общим решением будет .
Б. Если уравнение вида неразрешимо (или трудно разрешимо) как относительно , так и относительно , но допускает выражение и через некоторый параметр :
то поступаем следующим образом. Имеем . С другой стороны, , так что и ; отсюда
Таким образом, получаем общее решение данного дифференциального уравнения в параметрической форме
Пример 4. Решить уравнение .
Решение. Полагаем , тогда имеем
Отсюда , общее решение .
В. Уравнение вида . Пусть это уравнение разрешимо относительно , то есть .
Полагая , получим . Но и, следовательно, , так что
Таким образом — общее решение уравнения в параметрической форме ( — параметр).
Замечание. В формулах нельзя рассматривать как производную. В них является просто параметром.
Пример 5. Решить уравнение .
Решение. Положим , тогда
Итак, — общее решение.
Аналогично случаю Б можно пытаться решать уравнение методом введения параметра .
3°. Уравнения Лагранжа
Уравнение Лагранжа имеет вид
Полагая , дифференцируя по и заменяя на , приводим это уравнение к линейному относительно как функции . Находя решение этого последнего уравнения , получаем общее решение исходного уравнения в параметрической форме:
Кроме того, уравнение Лагранжа может иметь еще особые решения вида , где — корень уравнения .
Пример 6. Проинтегрировать уравнение .
Решение. Полагаем , тогда . Дифференцируя, находим
Получили уравнение первого порядка, линейное относительно ; решая его, находим
Подставляя найденное значение в выражение для , получим окончательно
Уравнения Клеро
Уравнение Клеро имеет вид .
Метод решения тот же, что и для уравнения Лагранжа. Общее решение уравнения Клеро имеет вид
Уравнение Клеро может иметь еще особое решение, которое получается исключением из уравнений .
Пример 7. Проинтегрировать уравнение .
Решение. Полагая , получаем . Дифференцируя последнее уравнение и заменяя на , найдем
Приравнивая нулю первый множитель, получаем , откуда и общее решение исходного уравнения есть , однопараметрическое семейство прямых. Приравнивая нулю второй множитель, будем иметь . Исключая из этого уравнения и из уравнения , получим — это тоже решение нашего уравнения (особое решение).
С геометрической точки зрения кривая есть огибающая семейства прямых, даваемых общим решением (рис. 14).
http://spravochnick.ru/matematika/differencialnye_uravneniya/uravnenie_klero/
http://mathhelpplanet.com/static.php?p=differentsialnye-uravneniya-pervogo-poryadka—ne-razreshennye-otnositelno-proizvodnoi