Решить уравнение онлайн wolfram alpha

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Решение «буквенных» уравнений в Wolfram|Alpha

Задача «выразить х из уравнения (с несколькими неизвестными)» встречается довольно часто. Ее можно рассматривать, как решение уравнения с буквенными коэффициентами. Поэтому логично, что Wolfram|Alpha использует для решения таких «буквенных» уравнений запрос solve, который обычно служит для решения уравнений с одним неизвестным.

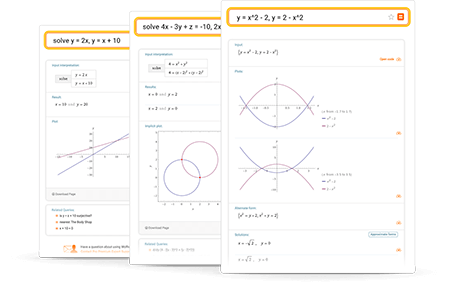
Вот простой пример такой задачи.

Запрос solve применительно к этому уравнению дает такой результат:

Здесь Wolfram|Alpha отдает приоритет отысканию переменной y. Возможно, полагая, что y это — функция, а x — ее аргумент? Кстати, тот же самый результат дает и запрос solve 2x+3y-1.

Если же из данного уравнения нужно найти именно х, то это следует указать явно. И вот, каким образом:

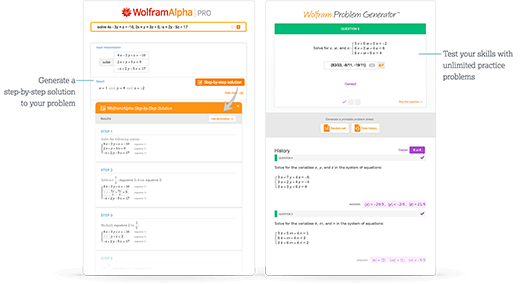
При этом, в отличие от первого варианта, здесь Wolfram|Alpha дает возможность посмотреть пошаговое решение задания с подробным текстовым комментарием:

(Эта замечательная особенность Wolfram|Alpha уже обсуждалась в одном из предыдущих постов Математика с Wolfram|Alpha: шаг за шагом. )

Итак, рассмотренный выше пример уже дает представление о том, как легко Wolfram|Alpha справляется с «буквенными» уравнениями. Однако, пойдет ли дело так же гладко, если вместо x и y взять другие буквы?

Запрос solve 2a+3b-1 дает следующее:

Однако, абсолютно аналогичный по структуре запрос solve 2n+3m-1 выводит совсем другой результат:

Конечно же! Логика здесь есть: Wolfram|Alpha по умолчанию считает неизвестным то, что обозначено буквой, расположенной ближе к концу алфавита. Но, если вы не уверены в своем знании английского алфавита, тогда, решая в Wolfram|Alpha буквенное уравнение, лучше каждый раз явно указывать неизвестную величину.

Естественно, теперь возникает вопрос: а что будет, если взять уравнение, которое содержит не два буквенных обозначения, а больше? Например, такое:

Как и следовало ожидать, здесь Wolfram|Alpha по запросу solve (без указания неизвестного) выводит решение квадратного уравнения относительно x:

Если же из данного уравнения нужно найти b, то запрос должен быть таким:

Аналогичным образом следует поступить, если ищем c:

Также ясно, что решение кубического уравнения

А вот, если нас интересует, как выражается из данного уравнения a, то запрос формулируем иначе:

Под конец, хочется задать Wolfram|Alpha вопрос посложнее. Например, сможет ли система решить такое «буквенное» уравнение?

Запрос solve без явного указания неизвестного выводит решение этого уравнения относительно z:

Если же нужно найти, к примеру, w, тогда, естественно, получим:

Что же касается решения трансцендентных «буквенных» уравнений, то все зависит от вида конкретного уравнения. Если уравнение допускает аналитическое решение, тогда это решение получается точно так же, как и ранее. Если же нет, тогда, по-возможности, Wolfram|Alpha выдает неявное решение в графическом виде.

Рассмотрим несколько типичных примеров.

Некоторые решения оказываются довольно неожиданными и по-своему красивыми:

Online Systems of Equations Solver

Solve equations and systems of equations with Wolfram|Alpha

A powerful tool for finding solutions to systems of equations and constraints

Wolfram|Alpha is capable of solving a wide variety of systems of equations. It can solve systems of linear equations or systems involving nonlinear equations, and it can search specifically for integer solutions or solutions over another domain. Additionally, it can solve systems involving inequalities and more general constraints.

Learn more about:

Tips for entering queries

Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about solving systems of equations.

Access instant learning tools

Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator

Learn more about:

What are systems of equations?

A system of equations is a set of one or more equations involving a number of variables.

The solutions to systems of equations are the variable mappings such that all component equations are satisfied—in other words, the locations at which all of these equations intersect. To solve a system is to find all such common solutions or points of intersection.

Systems of linear equations are a common and applicable subset of systems of equations. In the case of two variables, these systems can be thought of as lines drawn in two-dimensional space. If all lines converge to a common point, the system is said to be consistent and has a solution at this point of intersection. The system is said to be inconsistent otherwise, having no solutions. Systems of linear equations involving more than two variables work similarly, having either one solution, no solutions or infinite solutions (the latter in the case that all component equations are equivalent).

More general systems involving nonlinear functions are possible as well. These possess more complicated solution sets involving one, zero, infinite or any number of solutions, but work similarly to linear systems in that their solutions are the points satisfying all equations involved. Going further, more general systems of constraints are possible, such as ones that involve inequalities or have requirements that certain variables be integers.

Solving systems of equations is a very general and important idea, and one that is fundamental in many areas of mathematics, engineering and science.

Задача Коши онлайн

Данная задача возникает при поиске частного решения дифференциального уравнения. Наш онлайн калькулятор, построенные на основе системы Wolfram Alpha, позволяет найти решение задачи Коши для различных типов дифференциальных уравнений. Чтобы начать работу, необходимо ввести данные своей задачи (дифференциальное уравнение и начальные условия) в калькулятор.

Найти решение задачи Коши для дифференциального уравнения:

при заданных начальных условиях:

При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке .

Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения:

удовлетворяющее начальным условиям:

Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:

Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции полученной ранее:

Далее, поставляем начальные условия в функцию и её производную :

Решая полученную систему уравнений получаем значения произвольных постоянных и :

Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение:

Другие полезные разделы:

Оставить свой комментарий:

Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме