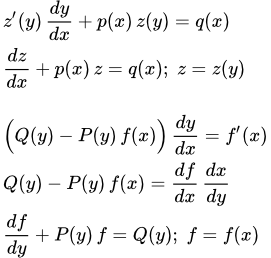Решить уравнение относительно переменной что это значит

Дифференциальные уравнения первого порядка, приводящиеся к линейным

Метод решения

К линейным уравнениям первого порядка приводится уравнения вида:
(1) ,
где z – функция от y ; p и q – функции от x .
Действительно, по правилу дифференцирования сложной функции:
.
Подставляя в (1), получаем уравнение, линейное относительно z :
.

Дифференциальные уравнения, линейные относительно переменной x

Ранее мы рассматривали уравнения, линейные относительно переменной y . То есть мы считали, что x является независимой переменной, а y является зависимой переменной. Однако, всегда стоит иметь в виду, что возможен противоположный подход. То есть можно считать переменную y независимой переменной, а x – зависимой переменной. На практике часто встречаются задачи, в которых уравнение линейно относительно переменной x , а не y . В общем виде такое уравнение можно записать так:
(2) ,
где P, Q, R –функции от y .

Покажем, что это уравнение линейно относительно переменной x . Для этого выполняем преобразования. Представим производную в виде отношения дифференциалов:
.
Тогда уравнение (2) примет вид:
.
Умножаем на и выполняем алгебраические преобразования:
;
.
Разделив на R ( y ) , приводим уравнение к виду:
,
где .
Это – линейное относительно x дифференциальное уравнение.

Пример решения дифференциального уравнения, приводящегося к линейному уравнению первого порядка

Решить уравнение:
(П.1) .

Подставим в (П.1):
.
Считаем, что y – это независимая переменная, а x – зависимая. То есть x – это функция от y . Умножим на :
(П.2) .
Делаем подстановку:
.
Здесь z – сложная функция от y , .
Дифференцируем по y . По правилу дифференцирования сложной функции:
.
Подставляем в (П.2):
;
.
Это линейное, относительно z , дифференциальное уравнение. Решаем его с помощью интегрирующего множителя. Умножаем уравнение на интегрирующий множитель e y :
;
;
.
Интегрируем по частям:

;

;
;
.
Переходим к переменной x :
;
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 05-08-2012 Изменено: 26-06-2015

Линейные уравнения с параметрами в 7-м классе (методические рекомендации)

Разделы: Математика

Известно, что в программе по математике для неспециализированных школ задачам с параметрами отводится незначительное место.
К задачам с параметрами, рассматриваемым в школьном курсе, относятся, например, задачи, в которых отыскивается решение линейных и квадратных уравнений в общем виде, исследуется количество их корней в зависимости от значений параметров.
Естественно, что такой небольшой класс задач не позволяет учащимся овладеть методами решения задач с параметрами. В результате, у учащихся возникает психологический барьер уже при «первом» знакомстве с параметрами — это неизвестное и известное, переменная и постоянная. Выход из сложившейся ситуации — включать задачи с параметрами в каждую тему.

• Для решения задач с параметрами требуется:

а) свободное владение навыками решения уравнений;
б) знание специфических преобразований, которые используются в уравнениях;
в) умение построить логическую цепочку рассуждений.

а) отработку навыков решения уравнений;
б) повышают интеллектуальный уровень ученика и его логическое мышление;
в) формируют навыки исследовательской деятельности;
г) повышают интерес к математике.

Прежде чем ввести понятие «параметр», учащимся необходимо напомнить роль букв в алгебре. Обратить внимание ребят на то, что за буквой скрывается число.
Предложите учащимся задания, в которых надо выразить одну переменную через другую. К этим задачам надо возвращаться постоянно, особенно в 7-м классе, поскольку умение выражать одну переменную через другую очень пригодится при решении задач по физике, где требуется вначале составить буквенное выражение и только затем подставить числовые значения.

Пример №2.
Выразить х : а) ах = а-1; б) (а+2) х = а-1; в) а х = а -1.
Укажите, при каких значениях а имеет смысл полученное выражение.
Найдите значение х при а=2; а=3; а= -10.
Повторите на простых примерах, что такое уравнение, что значит решить уравнение. При решении уравнений типа 2х-2=-1;14х=-4; 3-3х=1 обратите внимание учащихся на то, что мы выразили неизвестное, которое надо найти, через числа.
Покажите, что в уравнение, помимо неизвестного, могут быть введены и другие буквы, и буквенные выражения. Например, ах=а-1, (а+2)х=а-1, (а+2)х=(а+2)-1, а х=а -1.
При этом, как всегда в алгебре, мы полагаем, что буквы могут принимать любые числовые значения. Например, задавая произвольно значения а для уравнения ах=а-1 получаем
при а=2 имеем 2х=2-1; при а=3 имеем 3х=3-1; при а=0 имеем 0х=0-1; при а=-4 имеем -4х=-4-1.

Пример №3.
Дано уравнение ах=5а-9.
Напишите уравнение, которое получится, если а=10; а=-2; а=0.

Пример №4.
Решить уравнение относительно х:
х+2=а+7.
Решение: х=а+5.
Переменную, которую надо найти, будем называть неизвестной, а переменную, через которую будем выражать искомую неизвестную, назовем параметром.

• Параметр — это переменная величина, которая в процессе решения уравнения (задачи) считают фиксированной и относительно которойпроводится анализ полученного решения.
• Решить уравнение с параметром — этозначит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению.

Заметим, что в нашем примере параметр а может принимать любые значения.
Ответ запишем так: при любом значении параметра а

х=а+5 .
Основное, что нужно усвоить при первом «знакомстве» с параметром, это необходимость осторожного обращения с фиксированным, но неизвестным числом. Необходимость аккуратного обращения с параметром хорошо видна в примерах, где замена параметра числом делает задачу банальной. К таким задачам, например, относятся задачи, в которых требуется сравнить два числа.

Пример №5.
Сравнить числа: а) а и 3а;
б) -а и 3а.
Решение:
а) естественно рассмотреть три случая:
если а 3а; если а = 0, то а = 3а; если а > 0, то а 3а; если а = 0, то -а = 3а; если а > 0, то -а -1 уравнение имеет два корня.

Как было сказано ранее, к уравнениям с параметрами надо возвращаться постоянно. Поэтому, на конец учебного года можно вынести уравнения:
1) (а-3)х=а2-9;
2) (3-2а)х=4а2-12а+9;
3) (а2-4)х=а2-5а+6;
4) (а2-1)х=а3+1
Решение.1) (а2-1)=0, а=±1.
При а=1 уравнение имеет вид 0х=2. Следовательно, решений нет.
При а=-1 уравнение имеет вид 0х=0. Следовательно, х- любое число.

Задачи для самостоятельного решения.

Для всех значений параметров а и в решите уравнения:

1. (5а+1)х+25а2+10а+1=0;
2. ах-а=х-1;
3. (а2-4)х=а2+а-2;
4. (а2-1)х-а2+2а-1=0;
5. (а-2в)х+а+в=3;
6. 
7. каких значениях параметра а уравнение а2(х-2)=х+а-3 имеет бесконечное множество решений?
8. каком значении параметра а корень уравнения х+3=2х-а будет отрицательным числом?
9. каждого значения параметра а определить число корней уравнения |x-1| =а.
10. каждого значения параметра а определить число корней уравнения|5x-3| =а.

Используемая литература.

1. Газета «Математика». Учебно-методическое приложение к газете «Первое сентября»: Е.Пронина, « Линейные уравнения с параметрами» №12, 2000 г.; C.Неделяева, «Особенности решения задач с параметрами» №34, 1999 г.
2. Азаров А.И., Барвенов С.А., Федосенко В.С. Методы решения задач с параметрами. Математика для старшеклассников. Минск: «Аверсэв», 2003.
3. Мочалов В.В., Сильвестров В.В. Уравнения и неравенства с параметрами. Чебоксары: Изд-во Чувашского университета, 2004.
4. Соколовская С.И., ДухонМ.Ю. Линейные уравнения и неравенства с параметром. Пособие для учащихся старших классов. М., 2005.

Метод решения относительно одной переменной

Методы решения нелинейных уравнений и неравенств в целых числах

При решении нелинейных уравнений в целых и натуральных числах можно условно выделить следующие методы:

1. Метод разложения на множители;

2. Метод решения относительно одной переменной;

4. Метод остатков;

6. Метод доказательства от противного;

7. Метод параметризации уравнения;

8. Функционально-графический метод.

Метод разложения на множители

· Вынесение общих множителей за скобку.

Задание 1. Решить в целых числах уравнение 2х 3 +ху-7=0

Решение: Приведем уравнение к виду: х(2х 2 +у)=7. Так как , то рассмотрим четыре системы уравнений:

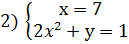
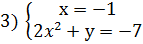
Из каждой системы получаем решения.

· Применение формул сокращенного умножения.

Задание 2. Найти все пары натуральных чисел, разность квадратов которых равна 55.

Решение: Запишем условие задачи в виде уравнения n 2 -k 2 =55 или (n-k)(n+k)=55. Так как (n+k)>0, то (n-k)>0, причем (n+k)>(n-k). Поскольку , то возможны только два случая:

. Из каждой системы получаем решения

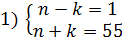
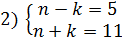
Задание 3. Решить в целых числах уравнение ху+3х-у=6..

Задание 3. Решить в целых числах уравнение ху+3х-у=6.

Решение: Запишем уравнение в виде х(у+3)-(у+3)=3 или (х-1)(у+3)=3. Так как , то рассмотрим четыре системы

Из каждой системы получаем решения.

Разложение квадратного трехчлена.

Задание 4. Решить в целых числах уравнение х 2 -3ху+2у 2 =11.

Решение: решим квадратное уравнение х 2 -3ху+2у 2 =11 относительно переменной х: х₁=у и х₂=2у. Тогда получаем: (х-у)(х-2у)=11. Так как … (продолжи решение)

Задание 5. Решить в целых числах уравнение 2х 2 -2ху++9х+у=2.

Решение: Перепишем уравнение в виде 2х 2 -х(2у-9)+у-2+а=аи разложим левую часть уравнения на множители как квадратный трехчлен относительно х. Найдем дискриминант D=4у 2 -44у+97-8а. Очевидно, если 97-8а=121, то дискриминант будет полным квадратом. При этом а=-3 и х= 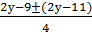. Отсюда х₁=0,5 и х₂=у-5. Уравнение принимает вид (2х-1)(х-у+5)=-3. (продолжи решение)

Метод решения относительно одной переменной

· Выделение целой части.

Задание 6 (МГУ, 1997). Найти все пары целых чисел х и у, удовлетворяющих уравнению 3ху+14х+17у+71=0

Решение: выразим из данного уравнения у через х: 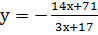. При этом следует отметить, что величина 3х+17 не равна нулю, так как х – целое число. Выделим из дроби в правой части этого равенства правильную Алгебраическую дробь (у которой степень числителя меньше степени знаменателя): . Умножим обе части последнего равенства на 3: или . Поскольку числа 3у и 14 – целые, то 3х+17 должно быть делителем числа 25, т.е. 3у+17= – всего 6 возможностей. Отсюда для х получаем три возможных значения: -4, -6, -14 (в остальных трех случаях х не является целым) Соответствующие значения у равны: -3, -13, -5.

Замечание: в данном примере суть выделения целой части состоит в избавлении переменной х из числителя. В решении был использован прием домножения обеих частей равенства на коэффициент при х в знаменателе. Этот прием домножения также удобно использовать при решении уравнений методом разложения на множители.

· Использование дискриминанта (неотрицательность).

Задание 7: Решить в целых числах уравнение 3(х 2 +ху+у 2 )=х+8у

Решение: Рассмотрим уравнение, как квадратное относительно х: 3(х 2 +ху+у 2 )-х-8у=0. Найдем дискриминант D=-27у 2 +90у+1. Данное уравнение имеет корни, если , т.е. -27у 2 +90у+1 . Т.к. то получаем, что . Перебирая эти значения, получаем решения уравнения.

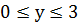
· Использование дискриминанта (полный квадрат).

Задание 7: Решить в целых числах уравнение х 2 -ху+у 2 =х+у

Решение: Рассмотрим уравнение как квадратное относительно х: х 2 –(у+1)х+у 2 -у=0. Его дискриминант D=-3у 2 +6у+1=t 2 должен быть квадратом некоторого целого числа t. Получаем новое уравнение: 3у 2 -6у-1+ t 2 =0; 3(у-1) 2 + t 2 =4. Из последнего уравнения следует, что t 2 4, .

1. Если t 2 =0, то уравнение 3(у-1) 2 =4 не имеет целого решения у.

2. Если t 2 =1, то уравнение 3(у-1) 2 =3 имеет целые решения у₁=2 и у₂=0. При у=2 получаем квадратное уравнение х 2 -3х+2=0 с корнями х=1 или х=2. При у=0 получаем квадратное уравнение х 2 -х=0 с корнями х=0 или х=1.

3. Если t 2 =4, то уравнение 3(у-1) 2 =0 имеет одно целое решение у=1. При у=1 получаем квадратное уравнение х 2 -2х=0 с корнями х=0 или х=2.

Метод оценки

· Использование известных неравенств.

Задание 8: Решить в натуральных числах уравнение

Решение: Пусть для определенности . Проведем перебор для первых значений неизвестной х.

1. Если х=1, то получаем неверное равенство 1+ , так как 1+ при любых натуральных у.

2. Если х=2, то получаем неверное равенство + , так как + при любых натуральных у.

3. Если х=3, то получаем + ; , у=6.

4. Если х=4, то получаем + ; , у=4.

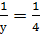
5. Если х=5, то получаем + ; , у= — не натуральное

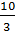
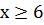
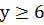
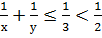
6. Пусть . По условию , следовательно, . Тогда , а значит, . Таким образом, при исходное уравнение решений не имеет.

Заметим, что в уравнении неизвестные х и у равноправны, поэтому снимая условие имеем еще одно решение (6;3). Кроме того, можно сделать вывод, что при исходное уравнение не имеет решений.

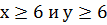
Задание 9: Решить в целых числах уравнение

Решение: Можно найти вначале решения только в натуральных числах, так как если (х₀; у₀; z₀) – решение, то, изменив знак у любых двух чисел этой тройки, снова получим решение. Данное уравнение умножим на 2xyz и воспользуемся неравенством ,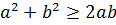

6xyz=2x 2 y 2 +2x 2 z 2 +2y 2 z 2 =(x 2 y 2 +x 2 z 2 )+(x 2 y 2 +y 2 z 2 )+(x 2 y 2 +y 2 z 2 ) 2x 2 yz+2y 2 xz+2z 2 xy=2xyz(x+y+z), откуда x+y+z 3. Но х,у, z – натуральные, поэтому х=у= z=1 единственное решение в натуральных числах. Остальные решения в натуральных числах. Остальные решения исходного уравнения таковы: (-1; -1; 1); (1; -1; -1); (-1; 1; -1).

Ответ: (1; 1; 1); (-1; -1; 1); (1; -1; -1); (-1; 1; -1)

· Приведение к сумме неотрицательных выражений

Задание 10: Решить в целых числах уравнение х+у=х 2 -ху+у 2

Решение: приведем уравнение к виду (х-1) 2 +(у-1) 2 +(х-у) 2 =2. Так как (х-1) 2 2, то имеем (х-1) 2 =0 или (х-1) 2 =1. Отсюда получаем три значения х: 1, 0, 2. Подставляя эти значения в исходное уравнение, найдем значения у.