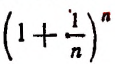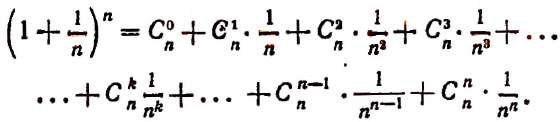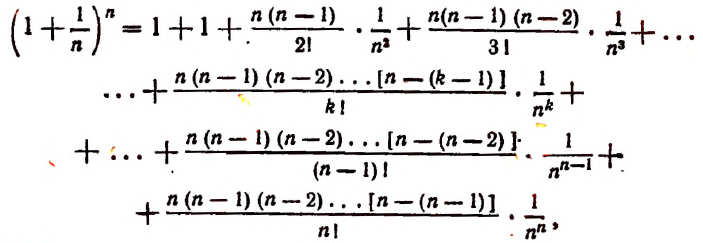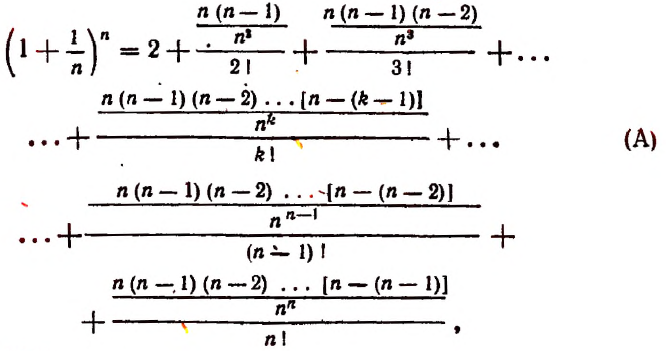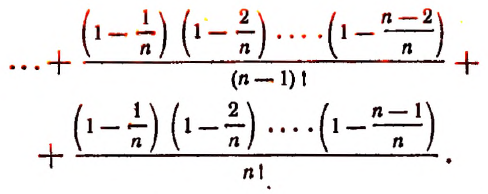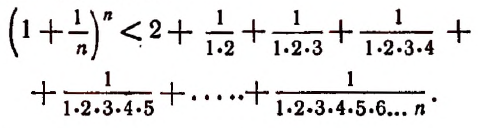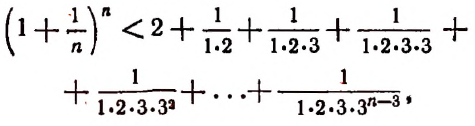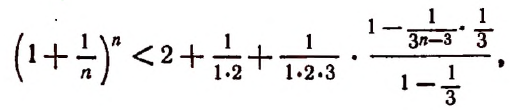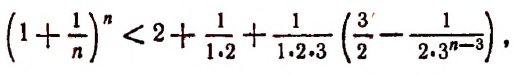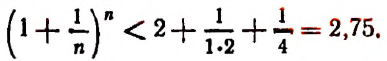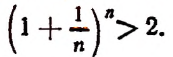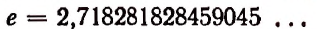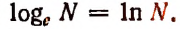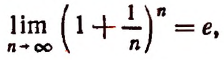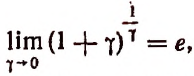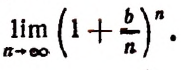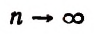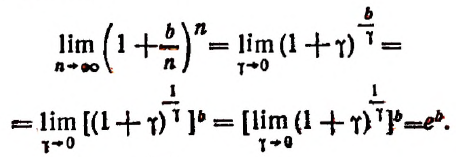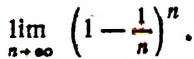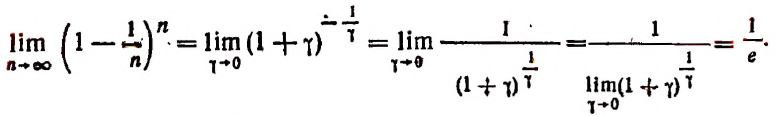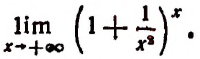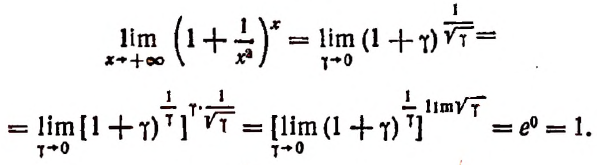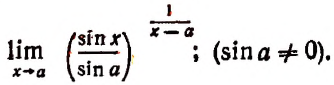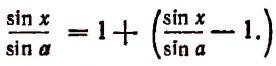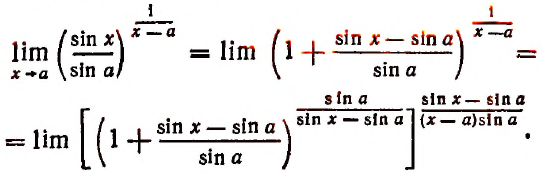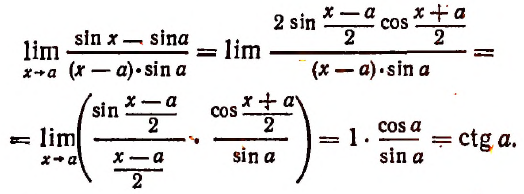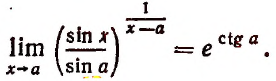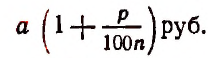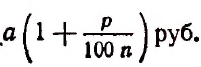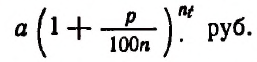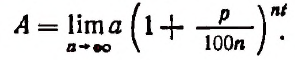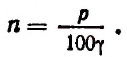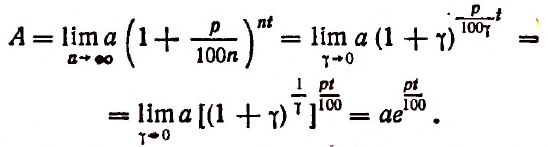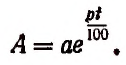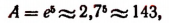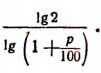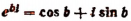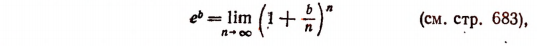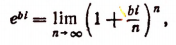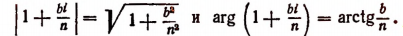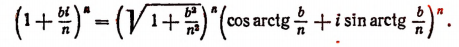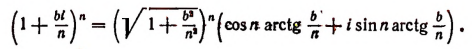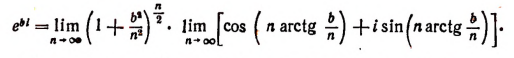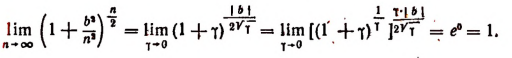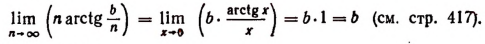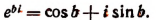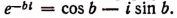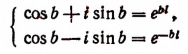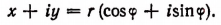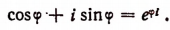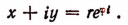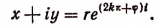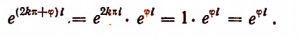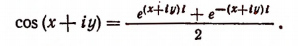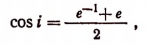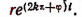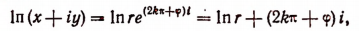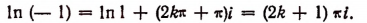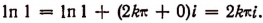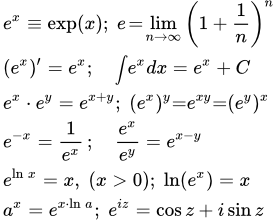Число е в математике и его применение с примерами решения
Возникновение числа е:
в котором n — натуральное число.
Изучение этого выражения необходимо для решения очень многих крайне важных задач (см., например, следующий параграф и главу «Производная, дифференциал, интеграл и их простейшие применения»).
Если мы станем натуральное число n неограниченно увеличивать, то величина выражения
станет величиной переменной. Эта переменная не стремится к единице, как это может показаться на первый взгляд. Действительно, мы сейчас убедимся в том, что при возрастании натурального числа n значение выражения
будет монотонно* возрастать, начиная со значения, равного двум. Например,
- Последовательность
называется возрастающей, если
неубывающей, если
убывающей, если
невозрастающей, если
Все такие последовательности называются монотонными.
Чтобы доказать, что переменная
монотонно возрастает при возрастании n, применим формулу бинома Ньютона:
Перепишем эту формулу в следующем виде:
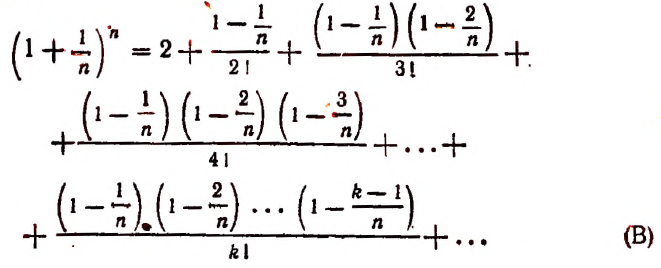
Все слагаемые в правой части этого равенства положительны.
При возрастании числа n правая часть этого равенства будет монотонно возрастать, так как будет возрастать число слагаемых и каждое слагаемое, начиная со второго.
Значит, доказано, что переменная 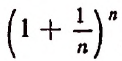
Теперь докажем, что, несмотря на то что переменная 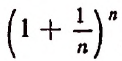
Из формулы (В) видно, что
Тем более будет верным неравенство
К сумме, написанной в квадратных скобках, применим формулу суммы членов конечной геометрической прогрессии. Тогда получим:
и тем более будет верным неравенство
Кроме этого, из формулы (А) видно, что всегда
Теперь перейдем к самому важному выводу.
Мы доказали, что переменная 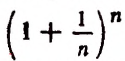
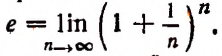
Число е выражается бесконечной непериодической десятичной дробью. Первые цифры этой дроби идут в таком порядке:
Напомним, что логарифмы по основанию е называются натуральными и обозначаются символом 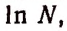
Применения числа е
Исходя из полученного равенства
можно доказать, что
где 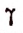
Последнее равенство можно сформулировать так:
Степень, основанием которой служит единица плюс бесконечно малое слагаемое 7, а показателем величина, обратная этому слагаемому, стремится к числу е, как к своему, пределу (доказательство опускается).
Обратим внимание на то, что основание этой степени стремится к единице, но, несмотря на это, сама степень не стремится к единице.
Рассмотрим пределы степеней, в которых основанием служит единица плюс бесконечно малое слагаемое, а показатель есть величина, обратная этому слагаемому.
Примеры:
1. Найти
Решение:
Полагая 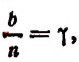
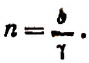
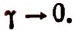
2. Найти
Полагая 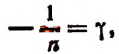
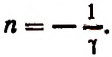
3. Найти
Полагая 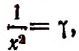
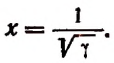
4. Найти
Представим 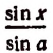
Здесь первое слагаемое есть единица, а второе, стоящее в скобках, есть величина бесконечно малая при
Таким образом, получим:
В квадратных скобках мы имеем степень, основанием которой является единица плюс бесконечно малое слагаемое, а показатель степени есть величина, обратная этому бесконечно малому слагаемому. Предел такой степени, как мы знаем, равен числу е.
Теперь найдем предел показателя степени, в который возводится выражение, стоящее в квадратных скобках:
Задачи:
1. Пусть банк принял вклад в a руб. и обязался присоединять процентные деньги к вкладу через каждую 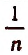
Одну n-ю часть года назовем установленным промежутком времени. Тогда один год будет содержать n, a t лет nt таких промежутков.
К концу первого промежутка времени вклад обратится в
Действительно, за первый промежуток времени процентные деньги, подлежащие присоединению к вкладу, будут равны 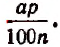
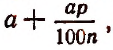
Обратим внимание на то, что для получения возросшей суммы за один промежуток времени достаточно вклад, имевшийся в начале промежутка, умножить на 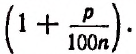
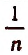
Значит, чтобы получить возросшую сумму к концу второго промежутка времени, достаточно вклад, образовавшийся к началу второго промежутка времени, умножить на множитель процентного наращения и т. д.
Итак, первоначальный вклад в а руб. обратится через t лет в
Теперь вообразим, что 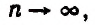
Полагая 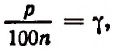
Итак, для органического роста вклада получилась следующая формула:
Например, при а = 1, р = 5 и f = 100
т. е. один рубль превращается через 100 лет приблизительно в 143 руб., если органический рост происходит по 5 годовых процентов.
2. Лесная делянка содержит в данный момент а куб. м древесины. Сколько окажется на этой делянке древесины через t лет, если органический рост древесины происходит по р годовых процентов.
Oтв. 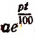
3. Численность населения города увеличивается ежегодно на р% (по отношению к началу года). Через сколько лет численность населения удвоится?
Отв.
Формула Эйлера
Формула Эйлера
В заключение этой главы приведем еще одно важное соотношение, найденное гениальным Эйлером, устанавливающее связь между тригонометрическими функциями и показательной функцией. Было доказано, что
где b — любое действительное число.
Обобщая этот результат, примем по определению, что
где b — любое действительное число, a i — мнимая единица. Теперь вычислим предел правой части последнего равенства.
Комплексное число 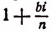
Пользуясь формулой Муавра, найдем, что
Вычислим каждый из пределов, входящих в правую часть последней формулы. Обозначив 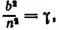
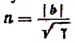
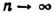
Далее, обозначим 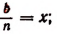
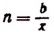
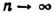
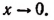
Эта формула и носит название формулы Эйлера.
Следствия из формулы Эйлера
1. Полагая в формуле Эйлера вместо b число 2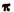
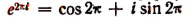
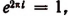
2. Полагая в формуле Эйлера вместо b число — b, получим, что
3. Пользуясь формулой Эйлера, можно представить любое комплексное число еще в одной новой форме.
Действительно, обозначив модуль комплексного числа х + iy буквой r, а главное значение аргумента буквой 
Но по формуле Эйлера
Выражение 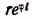
Справедливой будет и следующая запись:
4. Исходя из формулы Эйлера, мы можем находить тригонометрические функции от комплексного числа.
Действительно, обобщая формулу 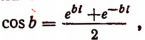
Полагая в последней формуле, например, х = 0 и у = 1, получим:
т. е. получим, что косинус мнимой единицы представляет собой действительное число.
5.Опираясь на формулу Эйлера, можно показать, что логарифм любого действительного или мнимого числа имеет в области комплексных чисел бесконечное множество различных значений. Представим комплексное число х + iy в показательной форме
где k — любое целое число.
Под выражением In r здесь понимается лишь действительное значение логарифма положительного числа r, которое легко вычисляется по таблицам логарифмов.
Примеры:
1. Модуль числа— 1 равен 1, а главное значение аргумента равно 
2. Модуль числа 1 есть 1, а главное значение аргумента 0. Поэтому
Под выражением In 1, написанным в левой части последнего равенства, подразумеваются все возможные комплексные значения логарифма единицы.
Под таким же выражением In 1, написанным в правой части, подразумевается лишь одно действительное значение логарифма единицы, т. е. нуль.
Числа е и 
С помощью этих чисел выражаются многие законы, по которым происходят процессы в природе. Числа е и 
Дополнение к числу е

Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Уравнения экспоненты по математике
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Экспонента представляет собой показательную функцию \[y(x) =e^x,\] производная которой равна самой функции. Экспоненту обозначают: \[e^x, exp(x), Exp(x) \]
Экспонента обладает свойствами показательной функции с основанием степени е > 1. Основанием степени экспоненты является число «е». Это иррациональное число. Оно примерно равно:
Выражение числа «е» через предел последовательности. Число «е» можно выразить через предел последовательности. Это, так называемый, второй замечательный предел:
Выражение числа е в виде ряда
\[e = 2+1/2!+1/3!+1/3!+ \cdots +1/n!+ \cdots \]
На графике представлена экспонента, \[e\] в степени \[x:\]
На графике видно, что экспонента монотонно возрастает.
Что касается основных формул, то они такие же, как и для показательной функции с основанием степени \[е.\]
Выражение показательной функции через экспоненту:
Где можно решить уравнение с экспонентой онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Экспонента, е в степени х
Определение
Экспоненту обозначают так , или .
Число e
Основанием степени экспоненты является число e . Это иррациональное число. Оно примерно равно
е ≈ 2,718281828459045.
Число e определяется через предел последовательности. Это, так называемый, второй замечательный предел:
.
Также число e можно представить в виде ряда:
.
График экспоненты
На графике представлена экспонента, е в степени х.
y ( x ) = е х
На графике видно, что экспонента монотонно возрастает.
Формулы
Основные формулы такие же, как и для показательной функции с основанием степени е .
Выражение показательной функции с произвольным основанием степени a через экспоненту:
.
Частные значения
Пусть y ( x ) = e x . Тогда
.
Свойства экспоненты
Экспонента обладает свойствами показательной функции с основанием степени е > 1 .
Область определения, множество значений
Экспонента y ( x ) = e x определена для всех x .
Ее область определения:
– ∞ .
Ее множество значений:
0 .
Экстремумы, возрастание, убывание
Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
| y = е х | |
| Область определения | – ∞ |
| Область значений | 0 |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 |
| + ∞ | |
| 0 |
Обратная функция
Производная экспоненты
Производная е в степени х равна е в степени х:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Комплексные числа
Действия с комплексными числами осуществляются при помощи формулы Эйлера:
,
где есть мнимая единица:
.
Выражения через гиперболические функции
Выражения через тригонометрические функции
Разложение в степенной ряд
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов . Опубликовано: 25-02-2014 Изменено: 09-06-2018
http://www.pocketteacher.ru/solve-equation-with-exponent-ru
http://1cov-edu.ru/mat_analiz/funktsii/eksponenta/
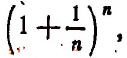
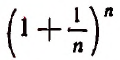
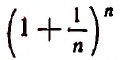

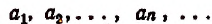 называется возрастающей, если
называется возрастающей, если 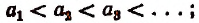 неубывающей, если
неубывающей, если 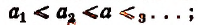 убывающей, если
убывающей, если 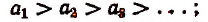 невозрастающей, если
невозрастающей, если 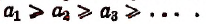 Все такие последовательности называются монотонными.
Все такие последовательности называются монотонными.