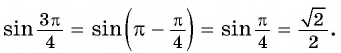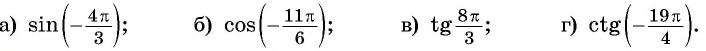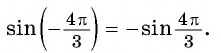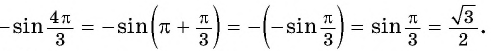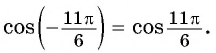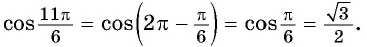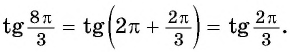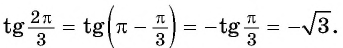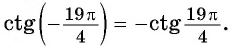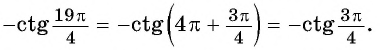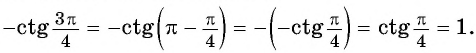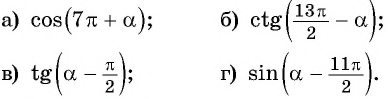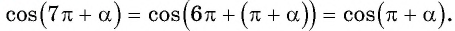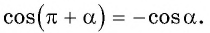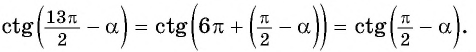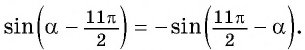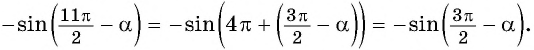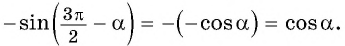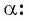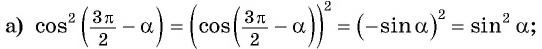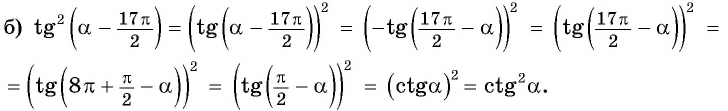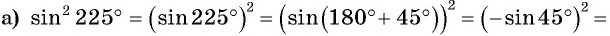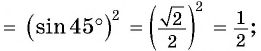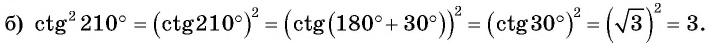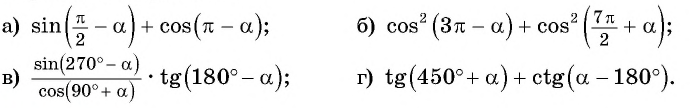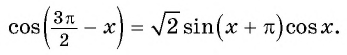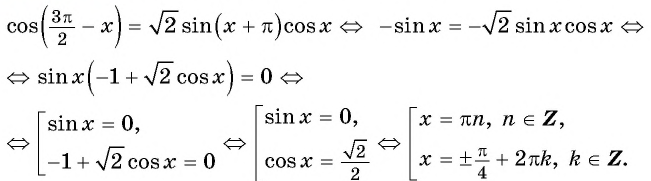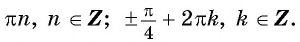Формулы приведения. Примеры из ЕГЭ
Как вы, наверное, уже обратили внимание, формулы приведения разработаны для углов, представленных в одном из следующих видов: \(\frac<\pi><2>+a\), \(\frac<\pi><2>-a\), \(π+a\), \(π-a\), \(\frac<3\pi><2>+a\), \(\frac<3\pi><2>-a\), \(2π+a\) и \(2π-a\). Аналогично их можно использовать для углов представленных в градусах: \(90^°+a\), \(90^°-a\), \(180^°+a\), \(180^°-a\), \(270^°+a\), \(270^°-a\), \(180^°+a\), \(180^°-a\).
К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
Как быстро получить любую формулу приведения
Для начала обратите внимание, что все формулы имеют похожий вид:
Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс или котангенс , он либо останется синусом, либо превратиться в косинус . А котангенс никогда не станет синусом или косинусом, он либо останется котангенсом, либо станет тангенсом. И так далее.
Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
— как определить знак перед конечной функцией (плюс или минус)?
— как определить меняется ли функция на кофункцию или нет?
Как определить знак перед конечной функцией (плюс или минус)?
Какой знак был у исходной функции в исходной четверти, такой знак и нужно ставить перед конечной функцией.
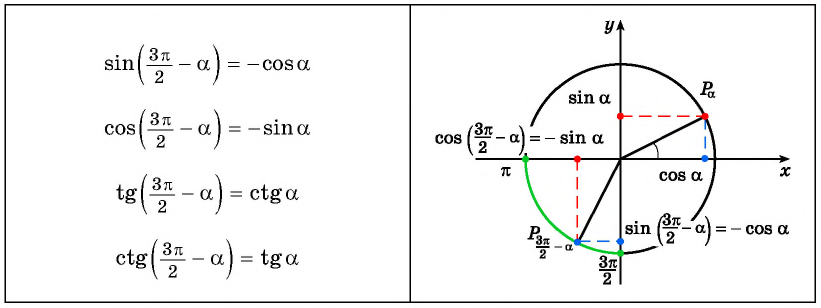
Например, выводим формулу приведения для \(cos(\frac<3\pi><2>-a) =. \) С исходной функцией понятно – косинус, а исходная четверт ь ?
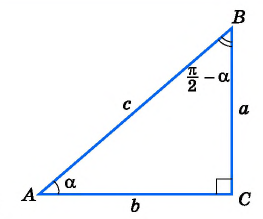
Для того, чтобы ответить на этот вопрос, представим, что \(a\) – угол от \(0\) до \(\frac<\pi><2>\), т.е. лежит в пределах \(0°…90^°\) (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол \(\frac<3\pi><2>-a\)?
Чтобы ответить на вопрос, надо от точки, обозначающей \(\frac<3\pi><2>\), повернуть в отрицательную сторону на угол \(a\).
В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус. Поэтому перед итоговой функцией будет стоят минус: \(cos(\frac<3\pi><2>-a)=-. \)
Менять ли функцию на кофункцию или оставить прежней?
Здесь правило еще проще:
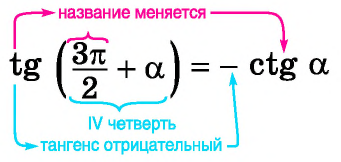
— если «точка привязки» \(\frac<\pi><2>\) (\(90^°\)) или \(\frac<3\pi><2>\) (\(270^°\))– функция меняется на кофункцию;
— если «точка привязки» \(π\) (\(180^°\)) или \(2π\) (\(360^°\)) – функция остается той же.
То есть, при аргументах исходной функции \(\frac<\pi><2>+a\), \(\frac<\pi><2>-a\), \(\frac<3\pi><2>+a\) или \(\frac<\pi><2>-a\), мы должны поменять функцию, а при аргументах \(π+a\), \(π-a\), \(2π+a\) или \(2π-a\) — нет. Для того, чтоб это легче запомнить, вы можете воспользоваться мнемоническим правилом, которое в школе называют «лошадиным правилом»:
Точки, обозначающие \(\frac<\pi><2>\) \((90^°)\) и \(\frac<3\pi><2>\) \((270^°)\), расположены вертикально, и если вы переводите взгляд с одной на другую и назад, вы киваете головой, как бы говоря «да».
Точки же, обозначающие \(π\) (\(180^°\)) и \(2π\) (\(360^°\)), расположены горизонтально, и если вы переводите взгляд между ними, вы мотаете головой, как бы говоря «нет».
Эти «да» и «нет» — и есть ответ на вопрос: «меняется ли функция?».
Таким образом, согласно правилу, в нашем примере выше \(\cos(\frac<3π><2>-a)=. \) косинус будет меняться на синус. В конечном итоге получаем, \(\cos(\frac<3π><2>-a)=-\sin\) \(a\). Это и есть верная формула приведения.
Примеры из ЕГЭ с формулами приведения:
Углы \(<41>^°\) и \(<49>^°\) нестандартные, поэтому «в лоб» без калькулятора вычислить непросто. Однако использовав формулы привидения, мы легко найдем правильный ответ.
Прежде всего, обратите внимание на один важный момент: \(49^°=90^°-41^°\). Поэтому мы можем заменить \(49^°\) на \(90^°-41^°\).
Теперь применим к синусу формулу приведения:
\(90^°-41^°\) – это первая четверть, синус в ней положителен. Значит, знак будет плюс;
\(90^°\)- находится на «вертикали» — функция меняется на кофункцию.
В числителе и знаменателе получились одинаковые косинусы. Сокращаем их.
Формулы приведения с примерами решения
При изучении геометрии вы установили, что
если
Свойство периодичности тригонометрических функций позволяет свести вычисление значений синуса, косинуса, тангенса и котангенса произвольного угла к вычислению значений этих функций при значениях аргумента, принадлежащих промежутку 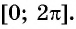
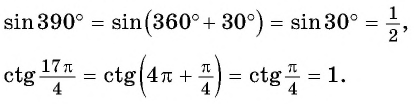
На практике принято сводить значения тригонометрических функций произвольного угла к вычислению значений этих функций для угла, принадлежащего промежутку 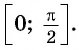
Это можно делать с помощью формул приведения.
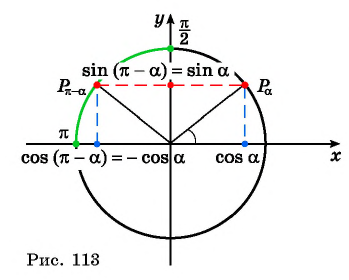
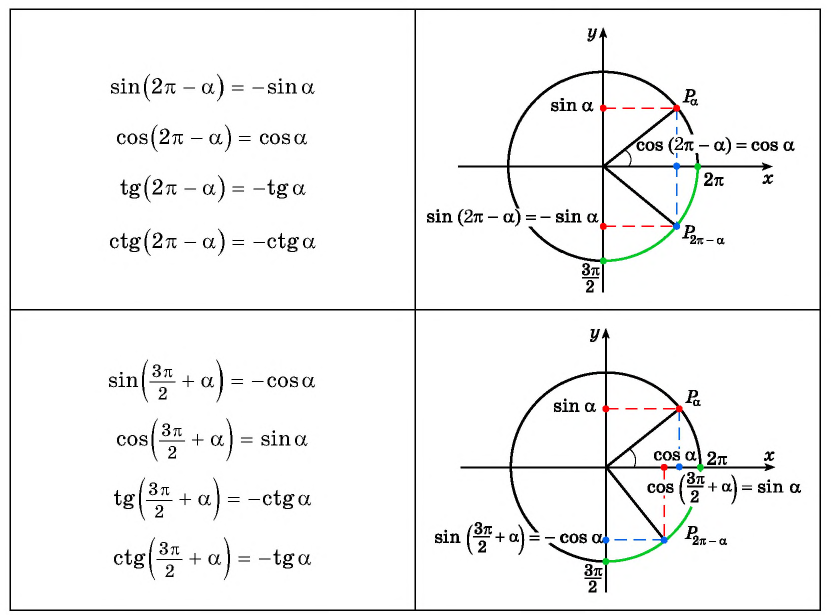
Рассмотрим промежуток 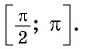
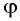
Например, 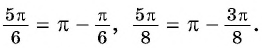
Поскольку ординаты точек 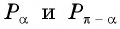
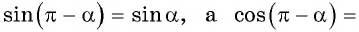
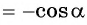
Тогда для 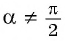
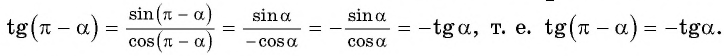
А для 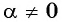
Вместе с тем любое число 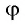
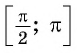
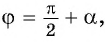
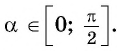
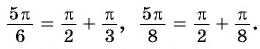
Так как ордината точки 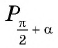
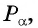
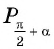
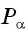
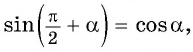
Для 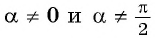
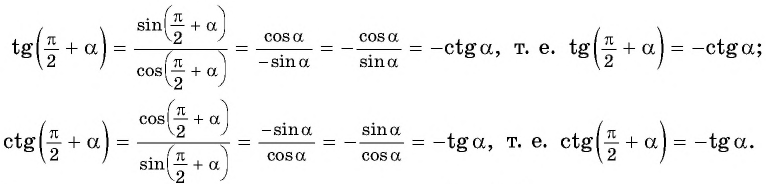
Так как любое число 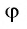
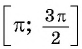
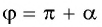
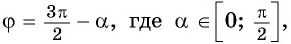
Поскольку любое число 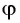
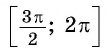
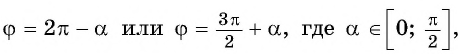
Проанализировав полученные формулы, можно заметить закономерности, позволяющие сформулировать правило, с помощью которого можно применять формулы приведения, не заучивая их:
В правой части формулы приведения ставится тот знак, который имеет в соответствующей четверти исходная функция, если считать, что угол 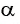
Если в формуле приведения аргумент имеет вид:
то название функции не меняется;
то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
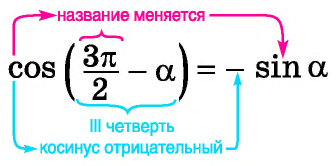
Например, применим полученное правило для выражения
- Если считать, что угол
— острый, то —
— угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».
- Поскольку аргумент имеет вид
то название функции «косинус» нужно поменять на «синус». Таким образом, получим:
Пример:
Приведите выражение к тригонометрической функции числа 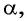
Решение:
а) 1. Так как 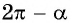
2. Поскольку аргумент имеет вид 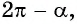
б) 1. Так как 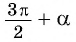
2.Поскольку аргумент имеет вид 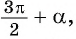
в) 1. Так как 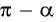
2. Поскольку аргумент имеет вид 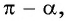
Пример:
Используйте формулы приведения и найдите значение выражения:
Решение:
Первый способ:
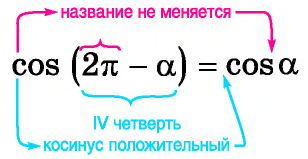
- Так как
угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».
- Поскольку аргумент имеет вид
то название функции «синус» не меняется. Значит,
Второй способ:
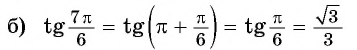
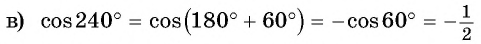
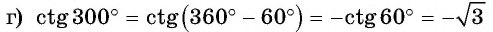
Пример:
Вычислите, используя формулы приведения:
Решение:
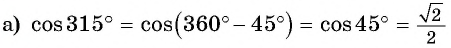
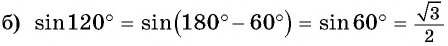

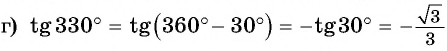
Пример:
Найдите значение выражения:
Решение:
а) Так как синус — нечетная функция, то
Применим формулы приведения:
б) Воспользуемся свойством четности косинуса и получим:
По формулам приведения:
в) Воспользуемся свойством периодичности тангенса и получим:
Применим формулы приведения:
г) Поскольку котангенс — нечетная функция, то
Используем свойство периодичности котангенса и получим:
Пример:
По формулам приведения:
Приведите к тригонометрической функции угла
Решение:
а) Используем свойство периодичности косинуса и получим:
По формулам приведения:
б) Воспользуемся свойством периодичности котангенса:
Применим формулы приведения:
в) Так как тангенс — нечетная функция, то 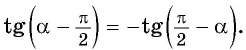
г) Поскольку синус — нечетная функция, то
Воспользуемся свойством периодичности синуса и получим:
По формулам приведения:
Пример:
Приведите к тригонометрической функции угла
Решение:
Пример:
Решение:
Пример:
Решение:
а) Применим формулы приведения:
б)Воспользуемся периодичностью косинуса и формулами приведения и получим:
в)Применим формулы приведения:
г) Используем периодичность тангенса, нечетность котангенса и формулы приведения:
Пример:
Решите уравнение:
Решение:
Применим формулы приведения и получим:
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Тригонометрические уравнения — формулы, решения, примеры
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:


Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`
Решение. Используя формулы приведения, имеем:
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.
Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a
`cos \varphi sin x + sin \varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt <3^2+4^2>`, получим:
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos \varphi sin x+sin \varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `\frac
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
http://www.evkova.org/formulyi-privedeniya
http://matemonline.com/dh/%D1%82%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F/trigonometricheskie-uravnenija/





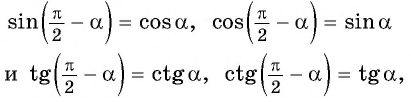
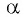
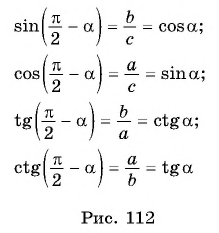
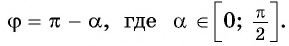
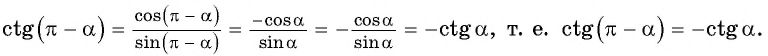
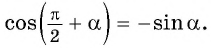
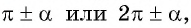 то название функции не меняется;
то название функции не меняется;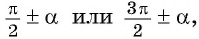 то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).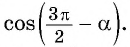
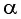 — острый, то —
— острый, то — 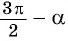 — угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».
— угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».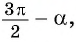 то название функции «косинус» нужно поменять на «синус». Таким образом, получим:
то название функции «косинус» нужно поменять на «синус». Таким образом, получим: 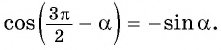
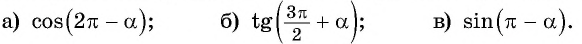
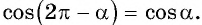
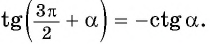
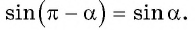

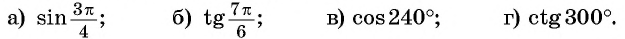
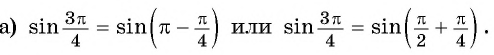
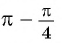 угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».
угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».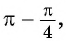 то название функции «синус» не меняется. Значит,
то название функции «синус» не меняется. Значит,