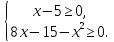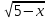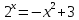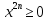Применение свойств функций для решения уравнений
В работе рассматриваются сособы решения уравнений с использованием свойств и характеристик функций: монотонности, ограниченности, области определенийи области значений функции.
Просмотр содержимого документа
«Применение свойств функций для решения уравнений»
II. Применение свойств функций для решения уравнений
Использование ОДЗ для решения уравнений .………….. 2стр
Монотонность функции и наличие корней уравнении…. 3стр
Используемая литература………………………………………. 10 стр
Найти и освоить приемы решения уравнений способами, позволяющими значительно сократить время нахождения корней уравнений.
В ходе сбора и изучения информации по данной теме, были найдены и изучены рациональные приемы решения уравнений с применением свойств монотонности, ограниченности функций, а также области определения и значений функций, позволяющие эффективно (практически устно) решать некоторые виды уравнений, рассмотренных в качестве примеров в нашей работе.
В наших школьных учебниках алгебры в основном изучаются такие методы и приемы решения уравнений как возведение в степень, замена переменной, применение тождественных преобразований, Но использование этих способов при решении некоторых видов уравнений приводит к довольно долгим и сложным преобразованиям, особенно если уравнения в левой и правой части которой находятся функции, имеющие различную природу.
В ходе наших поисков мы познакомились с одним из эффективных способов решения уравнений вида f(x)=g(x), который и демонстрируем в нашей работе. Это способ решения уравнений с использованием свойств функций.
Начнем с уравнений, которые можно решить, используя область определения функции или область допустимых значений переменной. Напомним, что множество значений переменной, при которых обе части данного уравнения (или неравенства) имеют смысл называют областью допустимых значений уравнения или неравенства. Рассмотрим такие уравнения, которые можно решить просто найдя ОДЗ.
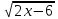
Пусть f(x) = 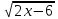
Значит правая часть уравнения должна быть неотрицательной, т.е. должно выполнятся условие 3−x ≥ 0, тогда x ≤ 3. Определяется системой двух неравенств: x≥3 и x ≤ 3. Получаем, что ОДЗ уравнения: х=3.Легко видеть, что 3 будет корнем исходного уравнения.
Приведем еще один пример уравнения:
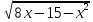
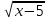
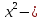
Решение: Найдем ОДЗ, решив систему неравенств
Решая неравенства этой системы получим 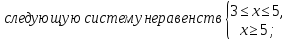
Монотонность функции и наличие корней уравнения.
Рассмотрим как применяются такое свойство функции как монотонность. Для успешного решения уравнения этим способом необходимо знать следующие утверждения: 1) если функция f (х) на некотором промежутке возрастает, а функция g(х) убывает на этом же промежутке, то уравнение f(х) = g(х) имеет на этом промежутке не более одного корня; 2) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)). Применение свойства продемонстрируем на следующих примерах:
1) x 1991 +1 =
1) В левой части этого уравнения стоит возрастающая функция на на R
в правой – убывающая на (-∞;5].
Если уравнение и будет иметь корень, то только на промежутке (-∞;5]. Легко заметить, что этот корень 1, и он, согласно теореме, единственный.
2) 5x 19 + 4x 3 +3х=12. Функция, стоящая в левой части уравнения является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.
3) 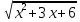
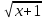
4) 2 x 15 + 3x=5/х. Функция f(x) = 5/х на каждом из промежутков (-∞;0) и (0:∞) убывает, а функция g (х) = 2 x 15 + 3x возрастает на каждом из них, поэтому наше уравнение на каждом из этих промежутков имеет не более одного корня. Убеждаемся, что это числа 1 и -1.
5) 2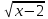
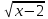
6) найти положительные корни уравнения
Функция 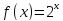
Убывает на промежутке [ 0; ∞). Следовательно, на промежутке [ 0; ∞) уравнение имеет не более одного корня. Подбором находим что х =1.
Функция 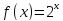
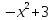
Рассмотрим, как можно применить к решению уравнений такое свойство функции как ограниченность. Метод, с помощью которого решаются уравнения с применением ограниченности функции, получил название метода мажорант. Ну, а само название метода происходит от французского слова majorer — объявлять большим. Мажорантой данной функции f(х) на множестве Р, называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р. Основная идея метода состоит в следующем: Пусть имеется уравнение f(х) = g(х) и существует такое такое число М, что для любого х из области определения f(х) и g(х) имеем f(х) ≤ М и g(х) ≥ М. Тогда уравнение f(х) = g(х) равносильно системе 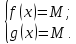
1. 
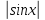
2. -1≤cosx≤1 или 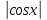
3.
4.

6.

1) Решим уравнение: + =0.
4и 10 степени – это четные числа, значит и при любом значении x. Тогда наше уравнение будет равносильно системе уравненийПервое уравнение имеет единственный корень – это число3, значит, если система и будет иметь решение, то не более одного. Проверкой убеждаемся, что3 является корнем и второго уравнения системы, а следовательно и исходного уравнения.
Заменим левую часть уравнения логарифмом, используя свойство разности логарифмов:
Представим дробь в виде , и используя неравенство Коши оценим подлогарифмическое выражение. Получаем (x + ) ≥ 4, а значит
log2 (x + ) ≥ 2. Таким образом, левая часть уравнения не меньше 2.
Рассмотрим правую часть уравнения. В правой части содержится квадратный трехчлен, поэтому выделив из него квадрат двучлена приходим к выводу, что данное выражение принимает значения не больше 2:
4 x – x 2 – 2 = – x 2 + 4 x – 2 = – ( – 4 x + 4 – 2) = – (x — 2) 2 + 2 = 2 – ( x — 2) 2
Получили, что правая часть уравнения не больше 2, т.к. (x — 2) 2 ≥ 0 при любых х. Значит, равенство левой и правой частей уравнения достигается, если они одновременно равны 2.
Из первого уравнения системы находим корень х = 2. Убеждаемся, что этот корень удовлетворяет и второму уравнению системы. Следовательно, решением исходного уравнения будет х = 2.
3) Решить уравнение:
В левой части уравнения стоит тригонометрическая функция, а в правой – сумма показательных. Формул, позволяющих находить корни в таких случаях, не существует. Оценим каждую из частей уравнения. Очевидно, что левая часть уравнения не больше 2. И так как
Поскольку 0, то причем равенство достигается только при x = 0. В данном случае
Получили, что левая часть уравнения не больше двух, а правая часть – больше или равняется двум. Таким образом, уравнение имеет решение, только если имеет решение система уравнений:
Проверкой убеждаемся, что x=0 – корень уравнения: . Значит число 0 – корень исходного уравнения. Получили ответ: x = 0.
Рассмотрим решение еще одного уравнения:
Рассмотрим две функции
Уравнение имеет решение, если наибольшее значение функции f(х) равно наименьшему значению функции g(х). Таким образом, уравнение имеет решение, только если обе части равны 2. И наше уравнение равносильно системе:
Решим первое уравнение системы:
Подставив данный корень во второе уравнение системы, получим верное равенство. Значит, решением исходного уравнения будут числа вида .
Функция y= (квадратичная функция) имеет наименьшее значение при , равное y(2)=4
Функция у= является возрастающей и, следовательно, принимает наименьшее значение при x=2
Правая часть уравнения, в силу ограниченности функции принимает значения не больше 2, поэтому исходное уравнение равносильно системе:
Так как 2-корень первого уравнения, то убедимся, что число 2-корень второго уравнения. Получаем:
Таким образом, 2-корень исходного уравнения.
Рассмотренные нами примеры могли быть решены и другими методами, но традиционные методы в данных конкретных примерах достаточно трудоемки. В нашей работе мы постарались продемонстрировать применение некоторых нестандартных приемов решения уравнений, основанных на свойствах и характеристиках функций. Планируем продолжить изучение нетрадиционных и эффективных приемов решения уравнений.
«Применение свойств функции при решении уравнений и неравенств»
Работа носит одновременно и прикладной и исследовательский характер. Для полноты исследования были рассмотрены следующие вопросы:
– Как отражаются свойства функции при решении уравнений и неравенств?
– Какие уравнения и неравенства решаются через определение свойств области определения, множества значений, инвариантности?
– Каков алгоритм решения?
– Рассмотрены задания с параметром, предлагаемых в материалах КИМ при подготовке к ЕГЭ.
В работе Екатерина исследовала большой круг задач и систематизировал их по внешнему виду.
Скачать:
| Вложение | Размер |
|---|---|
| nou_sv-v_funktsiy_05.04.pptx | 1.87 МБ |
| nou_sv-v_funktsiy_05.04.pptx | 1.87 МБ |
Предварительный просмотр:
Подписи к слайдам:
Применение свойств функции при решении уравнений и неравенств Выполнила работу: Галаева Екатерина МБОУ СОШ №149 Московского района Ученицы 11 «А» класса Научный руководитель: Фадеева И. А. Учитель математики
Основные направления: Изучение свойств функции: монотонность, ограниченность, область определения и инвариантность Узнать основные утверждения, которые наиболее часто используются при решении уравнений, неравенств и систем Решение задач из материалов КИМ для подготовке к ЕГЭ
Монотонность Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. f(x 1 ) f(x 2 ) x 1 x 2 f(x 1 ) f(x 2 ) x 1 x 2
Утверждение 1. Если функция у = f ( x ) монотонна, то уравнение f ( x ) = с имеет не более одного корня. x =2 f(x) = — монотонно убывающая, значит, других решений нет. Ответ: x =2
Утверждение 2. Если функция у = f ( x ) монотонно возрастает, а функция у = g ( x ) монотонно убывает, то уравнение f ( x ) = g ( x ) имеет не более одного корня. 2 — x = lg ( x +11) + 1 g ( x ) = 2 — x является монотонно убывающей, а функция f ( x ) = lg ( x + 11) + 1 монотонно возрастающей на области определения значит, уравнение f (х) = g ( x ) имеет не более одного корня. Подбором определяем, что х =-1 . Выше изложенное утверждение обосновывает единственность решения.
а ) f (х) ≤ g ( x ) в том и только в том случае, когда х ϵ (- ∞ ; x 0 ]; б) f (х) ≥ g ( x ) в том и только в том случае, когда х ϵ [х 0 ; +∞). Наглядный смысл этого утверждения очевиден Утверждение 3. Если функция у = f (х) монотонно возрастает на всей числовой прямой, функция у = g ( x ) монотонно убывает на всей числовой прямой и f (х 0 ) = g ( x 0 ), то справедливы следующие утверждения:
Решить неравенство Решение . Функция f (х) = монотонно возрастает на всей числовой прямой, а функция g ( x ) = монотонно убывает на всей области определения. Поэтому неравенство f (х) > g ( x ) выполняется, если х > 2. Добавим область определения неравенства. Таким образом , получим систему Ответ : (2; 5).
Утверждение 4. Если функция у = f (х) монотонно возрастает, то уравнения f (х)=х и f ( f (х))=х имеют одно и то же множество корней, независимо от количество вложений. Следствие. Если n — натуральное число, а функция у = f (х) монотонно возрастает, то уравнения f (х)=х и n раз имеют одно и то же множество корней.
Решить уравнение . Ответ: Решение. П ри x ≥1 правая часть уравнения не меньше 1, а левая часть меньше 1. Следовательно, если уравнение имеет корни, то любой из них меньше 1. При x ≤0 правая часть уравнения неположительная, а левая часть положительна, в силу того что . Таким образом, любой корень данного уравнения принадлежит интервалу (0; 1) Умножив обе части данного уравнения на х, и разделив на x числитель и знаменатель левой части, получим
Откуда = . Обозначив через t , где t 0, получим уравнение = t . Рассмотрим возрастающую на своей области определения функцию f ( t )= 1+ . Полученное уравнение можно записать в виде f ( f ( f ( f ( t ))))= t , и по следствию утверждения 4 оно имеет то же множество решений, что и уравнение f ( t )= t , т.е. уравнение 1 + = t , откуда . Единственным положительным корнем этого квадратного относительно уравнение является . Значит, , откуда , т.е. , или . Ответ:
Утверждение 1. Если max f ( x ) = с и min g ( x ) = с , то уравнение f ( x )= g ( x ) имеет то же множество решений, что и система Ограниченность Максимальное значение левой части равно 1 и минимальное значение правой части 1 , значит, решение уравнения сводиться к системе уравнений: , из второго уравнения находим возможный претендент x=0 , и убеждаемся, что он является решением и первого уравнения. Ответ: x=1 .
Решить уравнение Решение. Так как sin3x≤1 и cos4x≤1, левая часть данного уравнения не превосходит 7. Равной 7 она может быть в том и только том случае, если откуда где k , n ϵ Z . Остается установить, существуют ли такие целые k и n , при которых последняя система имеет решения. Ответ: Z
В задачах с неизвестными x и параметром a под областью определения понимают множество всех упорядоченных пар чисел ( x ; a ) , каждая из которых такова, что после подстановки соответствующих значений x и a во все входящие в задачу соотношения они будут определены. Пример 1. При каждом значение параметра a решите неравенство Решение. Найдем область определения этого неравенства. Из которых видно, что система Не имеет решений. Значит, область определения неравенства не содержит никаких пар чисел x и a , а поэтому неравенство не имеет решений. Область определения Ответ:
Инвариантность, т.е. неизменность уравнения или неравенства относительно замены переменной каким-либо алгебраическим выражением от этой переменной. Простейшим примером инвариантности является четность: если – четная функция, то уравнение инвариантно относительно замены x и – x , поскольку = 0. Инвариантность
Найти корни уравнения . Решение. Заметим, что пара инварианта относительно замене . Заменив в равенстве , получим . Умножив обе части данного равенства на 2 и вычтя из полученного равенства почленно равенство , находим 3 , откуда . Теперь осталось решить уравнение , откуда Корнями уравнения являются числа . Ответ: .
Найти все значения a , для каждого из которых уравнение имеет более трех различных решений. Решение задач с параметром Свойство монотонности
|x|= положительно X= |x|= Для существования двух корней числитель должен быть положителен. Поэтому При корни первого и второго уравнения совпадают, что не отвечает требованию условия: наличие более трех корней. Ответ : .
Найти все значения a , при каждом из которых уравнение имеет два корня. Преобразуем уравнение к виду И рассмотрим функцию f(x)= определенную и непрерывную на всей числовой прямой . График этой функции представляет собой ломаную, состоящую из отрезков прямых и лучей, каждое звено которой является частью прямой вида y= kt+l . f(x)= При любом раскрытие модуля первого выражения k не превосходит 8, поэтому возрастание и убывание функции f(x) будет зависеть от раскрытия второго модуля. При x f(x) будет убывать, а при x возрастать. То есть, при x=3 функция будет принимать наибольшее значение. Для того чтобы уравнение имело два корня, необходимо, чтобы f(3) Свойство монотонности
f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | — | 3+a | | 3+a | | 3+a | 3+a a Ответ: a
Найти все значения параметра а , при каждом из которых для любого действительного значения х выполнено неравенство Перепишем неравенство в виде , введем новую переменную t = и рассмотрим функцию f ( t ) = , определенную и непрерывную на всей числовой прямой. График этой функции представляет собой ломаную, состоящую из отрезков прямых и лучей, каждое звено которой является частью прямой вида , где к
Подписи к слайдам:
Применение свойств функции при решении уравнений и неравенств Выполнила работу: Галаева Екатерина МБОУ СОШ №149 Московского района Ученицы 11 «А» класса Научный руководитель: Фадеева И. А. Учитель математики
Основные направления: Изучение свойств функции: монотонность, ограниченность, область определения и инвариантность Узнать основные утверждения, которые наиболее часто используются при решении уравнений, неравенств и систем Решение задач из материалов КИМ для подготовке к ЕГЭ
Монотонность Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. f(x 1 ) f(x 2 ) x 1 x 2 f(x 1 ) f(x 2 ) x 1 x 2
Утверждение 1. Если функция у = f ( x ) монотонна, то уравнение f ( x ) = с имеет не более одного корня. x =2 f(x) = — монотонно убывающая, значит, других решений нет. Ответ: x =2
Утверждение 2. Если функция у = f ( x ) монотонно возрастает, а функция у = g ( x ) монотонно убывает, то уравнение f ( x ) = g ( x ) имеет не более одного корня. 2 — x = lg ( x +11) + 1 g ( x ) = 2 — x является монотонно убывающей, а функция f ( x ) = lg ( x + 11) + 1 монотонно возрастающей на области определения значит, уравнение f (х) = g ( x ) имеет не более одного корня. Подбором определяем, что х =-1 . Выше изложенное утверждение обосновывает единственность решения.
а ) f (х) ≤ g ( x ) в том и только в том случае, когда х ϵ (- ∞ ; x 0 ]; б) f (х) ≥ g ( x ) в том и только в том случае, когда х ϵ [х 0 ; +∞). Наглядный смысл этого утверждения очевиден Утверждение 3. Если функция у = f (х) монотонно возрастает на всей числовой прямой, функция у = g ( x ) монотонно убывает на всей числовой прямой и f (х 0 ) = g ( x 0 ), то справедливы следующие утверждения:
Решить неравенство Решение . Функция f (х) = монотонно возрастает на всей числовой прямой, а функция g ( x ) = монотонно убывает на всей области определения. Поэтому неравенство f (х) > g ( x ) выполняется, если х > 2. Добавим область определения неравенства. Таким образом , получим систему Ответ : (2; 5).
Утверждение 4. Если функция у = f (х) монотонно возрастает, то уравнения f (х)=х и f ( f (х))=х имеют одно и то же множество корней, независимо от количество вложений. Следствие. Если n — натуральное число, а функция у = f (х) монотонно возрастает, то уравнения f (х)=х и n раз имеют одно и то же множество корней.
Решить уравнение . Ответ: Решение. П ри x ≥1 правая часть уравнения не меньше 1, а левая часть меньше 1. Следовательно, если уравнение имеет корни, то любой из них меньше 1. При x ≤0 правая часть уравнения неположительная, а левая часть положительна, в силу того что . Таким образом, любой корень данного уравнения принадлежит интервалу (0; 1) Умножив обе части данного уравнения на х, и разделив на x числитель и знаменатель левой части, получим
Откуда = . Обозначив через t , где t 0, получим уравнение = t . Рассмотрим возрастающую на своей области определения функцию f ( t )= 1+ . Полученное уравнение можно записать в виде f ( f ( f ( f ( t ))))= t , и по следствию утверждения 4 оно имеет то же множество решений, что и уравнение f ( t )= t , т.е. уравнение 1 + = t , откуда . Единственным положительным корнем этого квадратного относительно уравнение является . Значит, , откуда , т.е. , или . Ответ:
Утверждение 1. Если max f ( x ) = с и min g ( x ) = с , то уравнение f ( x )= g ( x ) имеет то же множество решений, что и система Ограниченность Максимальное значение левой части равно 1 и минимальное значение правой части 1 , значит, решение уравнения сводиться к системе уравнений: , из второго уравнения находим возможный претендент x=0 , и убеждаемся, что он является решением и первого уравнения. Ответ: x=1 .
Решить уравнение Решение. Так как sin3x≤1 и cos4x≤1, левая часть данного уравнения не превосходит 7. Равной 7 она может быть в том и только том случае, если откуда где k , n ϵ Z . Остается установить, существуют ли такие целые k и n , при которых последняя система имеет решения. Ответ: Z
В задачах с неизвестными x и параметром a под областью определения понимают множество всех упорядоченных пар чисел ( x ; a ) , каждая из которых такова, что после подстановки соответствующих значений x и a во все входящие в задачу соотношения они будут определены. Пример 1. При каждом значение параметра a решите неравенство Решение. Найдем область определения этого неравенства. Из которых видно, что система Не имеет решений. Значит, область определения неравенства не содержит никаких пар чисел x и a , а поэтому неравенство не имеет решений. Область определения Ответ:
Инвариантность, т.е. неизменность уравнения или неравенства относительно замены переменной каким-либо алгебраическим выражением от этой переменной. Простейшим примером инвариантности является четность: если – четная функция, то уравнение инвариантно относительно замены x и – x , поскольку = 0. Инвариантность
Найти корни уравнения . Решение. Заметим, что пара инварианта относительно замене . Заменив в равенстве , получим . Умножив обе части данного равенства на 2 и вычтя из полученного равенства почленно равенство , находим 3 , откуда . Теперь осталось решить уравнение , откуда Корнями уравнения являются числа . Ответ: .
Найти все значения a , для каждого из которых уравнение имеет более трех различных решений. Решение задач с параметром Свойство монотонности
|x|= положительно X= |x|= Для существования двух корней числитель должен быть положителен. Поэтому При корни первого и второго уравнения совпадают, что не отвечает требованию условия: наличие более трех корней. Ответ : .
Найти все значения a , при каждом из которых уравнение имеет два корня. Преобразуем уравнение к виду И рассмотрим функцию f(x)= определенную и непрерывную на всей числовой прямой . График этой функции представляет собой ломаную, состоящую из отрезков прямых и лучей, каждое звено которой является частью прямой вида y= kt+l . f(x)= При любом раскрытие модуля первого выражения k не превосходит 8, поэтому возрастание и убывание функции f(x) будет зависеть от раскрытия второго модуля. При x f(x) будет убывать, а при x возрастать. То есть, при x=3 функция будет принимать наибольшее значение. Для того чтобы уравнение имело два корня, необходимо, чтобы f(3) Свойство монотонности
f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | — | 3+a | | 3+a | | 3+a | 3+a a Ответ: a
Найти все значения параметра а , при каждом из которых для любого действительного значения х выполнено неравенство Перепишем неравенство в виде , введем новую переменную t = и рассмотрим функцию f ( t ) = , определенную и непрерывную на всей числовой прямой. График этой функции представляет собой ломаную, состоящую из отрезков прямых и лучей, каждое звено которой является частью прямой вида , где к < 0 (поскольку при любом варианте «раскрытия» модулей коэффициент при t будет отрицательным). Следовательно , функция y = f (х) убывает на (—∞; +∞).
Так как , то t ϵ [—1; 1]. В силу монотонного убывания функции у = f ( t ) достаточно проверить левый край данного отрезка. З . А истинным является Значит , , что возможно, только если числа и и v одного знака либо какое-нибудь из них равно нулю. , = ( ) ( ) 0. Разложив квадратные трехчлены на множители, получим неравенство ( , из которого находим, что а ϵ (—∞; —1] U <2>U [ 4; +∞ ). Ответ: (—∞; — 1] U <2>U [4; +∞).
Пример 2. Найти все значения параметра , при каждом из которых система уравнений Решение. Поскольку и sin x 1, из первого уравнения следует, что a 6. Поскольку из второго уравнения системы следует, что a 0. Таким образом, 0 .Третье уравнение системы, раскрывая скобки в левой его части и приводя подобные слагаемые, можно переписать так: . Поскольку , из последнего уравнения следует, что , откуда a . Учитывая все 3 неравенства 0 , получаем, что допустимыми значениями параметра a являются только 0 и 6 . Пусть a 0 . Тогда из второго уравнения данной системы получим y .Поэтому первое уравнение системы примет вид sin x , откуда x , n Z .При a , x , n Z , y третье уравнение системы, очевидно, выполнено. Пусть a . Тогда левая часть первого уравнения данной системы не меньше 6, а правая не больше 6. Равенство возможно, если y Тогда второе уравнение данной системы принимает вид , и, значит, z При a x , последнее уравнение данной системы принимает вид . Из двух значений z только z принимает вид . Ответ: ( , k , при a=6 Свойство ограниченности
Решение. Необходимо выполнение условия ,откуда . При x = уравнение примет вид . Получим уравнение откуда или . Корнями двух последних уравнений являются При этих значениях параметра число -7 является корнем уравнения. При уравнение примет вид . Корнями того уравнения являются числа Значит, при 5 уравнение имеет больше одного корня. При и уравнение принимает вид . Теперь раскрываем модуль При уравнение сводится к уравнению , откуда Последнее уравнение, квадратное относительно , не имеет корней в силу отрицательности дискриминанта. При уравнение принимает вид и имеет единственный корень При получаем уравнение , откуда . И оно тоже не имеет корней как и при . Следовательно, при данное уравнение имеет единственный корень. Ответ: <3;7 >. Пример 3 . Найти все значения параметра a ,при каждом из которых уравнение имеет единственный корень. Свойство инвариантности
Свойство инвариантности Пример 4. Найти все значения параметра a , при каждом из которых система уравнений имеет единственное решение. Решение. Заметим, что если ( ) решение системы, то и ( ) Решение системы. Следовательно , для единственности решения необходимо, чтобы выполнялось условие . При y система имеет вид Если x Пусть a Тогда данная система имеет вид Поскольку Тогда Таким образом , 3 Следовательно, 3 , причём знак равенства возможен только в случае, когда 3 Получаем систему откуда Значит, при a данная система имеет единственное решение (-1;0). При a система имеет более одного корня. Ответ: a
Итоги моей работы В своей работе я изучила свойства функций: монотонность, ограниченность, область определения и инвариантность. Узнала очень много основных утверждений. Данные знания значительно упрощают задания с параметрами, которые имеют ужасающий вид. Систематизация задач по внешнему виду. Р ешение заданий типа 20. Цели , которые я поставила перед собой были достигнуты .
Применение свойств функций для решения уравнений
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Учитель математики: Гасраталиева Расинат Магомедовна
Применение свойств функций для решения уравнений
Найти и освоить приемы решения уравнений способами, позволяющими значительно сократить время нахождения корней уравнений.
В ходе сбора и изучения информации по данной теме, были найдены и изучены рациональные приемы решения уравнений с применением свойств монотонности, ограниченности функций, а также области определения и значений функций, позволяющие эффективно (практически устно) решать некоторые виды уравнений, рассмотренных в качестве примеров в нашей работе.
В наших школьных учебниках алгебры в основном изучаются такие методы и приемы решения уравнений как возведение в степень, замена переменной, применение тождественных преобразований, Но использование этих способов при решении некоторых видов уравнений приводит к довольно долгим и сложным преобразованиям, особенно если уравнения в левой и правой части которой находятся функции, имеющие различную природу.
В ходе наших поисков мы познакомились с одним из эффективных способов решения уравнений вида f(x)=g(x), который и демонстрируем в нашей работе. Это способ решения уравнений с использованием свойств функций.
В предлагаемой статье речь идет о нестандартных приемах решения уравнений, основанных на простых и хорошо известных учащимся свойствах и характеристиках функций, таких как непрерывность, монотонность наибольшее и наименьшее значение. Используя предлагаемые автором задачи и методы их решения, учитель сможет сформировать у учащихся более широкий взгляд на область применения различных этих свойств. Ведь не секрет, что в стандартном курсе школьной математики свойства функций применяются в основном для построения их графиков.
В соответствии с обязательным минимумом содержания среднего (полного) общего образования, утвержденным Министерством образования РФ (пр. №56 от 30.06.99), все учащиеся должны знать три основных метода решения уравнений:
Разложение на множители,
Использование свойств функций.
Рассмотрим на конкретных примерах сущность третьего метода. Этот метод применяется тогда, когда уравнение F(x)=G(x) в результате преобразований или замены переменных не может быть приведено к тому или иному стандартному уравнению, имеющему определенный алгоритм решения. Продемонстрируем использование некоторых свойств функций к решению уравнений указанного выше вида в случае, когда F(x) и G(x) — любые элементарные функции.
Монотонность функции и наличие корней уравнения.
Рассмотрим как применяются такое свойство функции как монотонность. Для успешного решения уравнения этим способом необходимо знать следующие утверждения: 1) если функция f (х) на некотором промежутке возрастает, а функция g(х) убывает на этом же промежутке, то уравнение f(х) = g(х) имеет на этом промежутке не более одного корня; 2) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)). Применение свойства продемонстрируем на следующих примерах:
1) В левой части этого уравнения стоит возрастающая функция на на R
в правой – убывающая на (-∞;5].
Если уравнение и будет иметь корень, то только на промежутке (-∞;5]. Легко заметить, что этот корень 1, и он, согласно теореме, единственный.
2) 5×19+ 4×3+3х=12. Функция, стоящая в левой части уравнения является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.
3) +=2. Областью определения функции, стоящей в левой части, является промежуток [-1; ∞). На этом промежутке функция возрастает. Следовательно, корень, равный -1 – единственный.
4) 2 x15 + 3x=5/х. Функция f(x) = 5/х на каждом из промежутков (-∞;0) и (0:∞) убывает, а функция g (х) = 2 x15+ 3x возрастает на каждом из них, поэтому наше уравнение на каждом из этих промежутков имеет не более одного корня. Убеждаемся, что это числа 1 и -1.
5) 2= 9/х – 1.Функция f(x)= 2 на промежутке [ 2; ∞) возрастает, а функция g (х) = 9/х – 1 на этом же промежутке убывает, значит уравнение имеет не более одного корня на этом промежутке. И этот корень равен 3.
6) найти положительные корни уравнения
Функция возрастает на R. g (х)=
Убывает на промежутке [ 0; ∞). Следовательно, на промежутке [ 0; ∞) уравнение имеет не более одного корня. Подбором находим что х =1.
Функция возрастает на(0; ∞) . а функция g (х)= на этом промежутке убывает. Значит, уравнение будет иметь корни только на промежутке (0; ∞). Подбором находим корень уравнения –это число 2.
Использование области определения и области значения функций
Решение: Множество решений этого уравнения совпадает с областью определения функции . Областью определения этой функции (в соответствии с определением степени с рациональным показателем) является множество положительных действительных чисел.
Решить уравнение sinxctgx=cosx.
Решение: Множество решений этого уравнения совпадает с областью определения уравнения. Область определения уравнения – это общая часть областей определения функций, входящих в уравнение. Следовательно, множество решений уравнения – множество всех действительных чисел, кроме x=k, где kZ.
Ответ: xk, где kZ.
Решение: У этого уравнения нет корней, так как область значений функции при x1 есть множество неотрицательных чисел, а функция при всех x принимает отрицательные значения.
Ответы: а) x>0, x1; б) x1; в) x0; г) x0; д) Нет корней; е) x0.
Использование экстремальных значений функций
Сущность этого способа решения уравнений в том, что оцениваются правая и левая части уравнения F(x)=G(x) и, если одна из функций принимает значение не меньше некоторого числа А, а другая – не больше этого же числа А, то данное уравнение заменяется системой уравнений:
Этот способ может быть применен к решению следующих уравнений:
в обеих частях уравнения стоят функции разного вида;
в одной части уравнения функция, ограниченная сверху, а в другой – ограниченная снизу;
в одной части уравнения стоит функция, ограниченная сверху или снизу, а в другой – конкретное число.
Рассмотрим конкретные примеры.
2.1 Решить уравнение
Решение: Оценим правую и левую части уравнения:
Оценка частей уравнения показывает, что левая часть не меньше, а правая не больше двух при любых допустимых значениях переменной x. Следовательно, данное уравнение равносильно системе
Первое уравнение системы имеет только один корень х=-2. Подставляя это значение во второе уравнение получаем верное числовое равенство:
2.2 Решить уравнение
Решение: левая часть уравнения не больше двух, а правая – не меньше двух, следовательно, данное уравнение равносильно системе:
Второе уравнение в этой системе имеет единственный корень х=0. Подставляя найденное значение х в первое уравнение, получаем верное числовое равенство.
2.3 Решить уравнение
Решение: Оценим левую часть уравнения: , следовательно, . Получили, что в данном уравнении левая часть не больше восьми, а правая часть равна девяти при всех действительных значениях переменной х, поэтому данное уравнение не имеет корней.
Ответ: нет корней.
2.4 Решить уравнения:
Ответы: а) ; б) 0; в) 0; г) 0.5; д) 1; е) нет корней.
Использование монотонности функций
Этот способ основан на следующих теоретических фактах:
Если одна функция возрастает, а другая убывает на одном и том же промежутке, то графики их либо только один раз пересекутся, либо вообще не пересекутся, а это означает, что уравнение F(x)=G(x) имеет единственное решение, либо вообще не имеет решений;
Если на некотором промежутке одна из функций убывает (возрастает), а другая принимает постоянные значения, то уравнение F(x)=G(x) либо имеет единственный корень, либо не имеет корней.
Сущность этого способа состоит в том, исследуются на монотонность левая и правая части уравнения и, если оказывается, что функции удовлетворяют какому — либо из приведенных условий, то найденное подбором решение будет единственным корнем уравнения.
Этот способ можно использовать для решения следующих типов уравнений:
уравнения, в обеих частях которых стоят функции разного вида;
уравнения, в одной части которых убывающая, а в другой – возрастающая на данном промежутке функции;
уравнения, одна часть которых – возрастающая или убывающая функция, а вторая – число.
3.1 Решить уравнение
Решение: область определения данного уравнения x>0. Исследуем на монотонность функции . Первая из них –убывающая (так как это — логарифмическая функция с основанием больше нуля, но меньше единицы), а вторая – возрастающая (это линейная функция с положительным коэффициентом при х). Подбором легко находится корень уравнения х=3, который является единственным решением данного уравнения.
3.2 Решить уравнение
Решение: Данному уравнению удовлетворяет число х=2. Проверим, удовлетворяют ли функции, образующие уравнение, условиям, при которых можно утверждать, что других корней нет. Сначала рассмотрим . Исследуем ее на монотонность с помощью производной: . Решаем биквадратное уравнение
поэтому при всех значениях хR., следовательно, функция f(x)- возрастающая.
Теперь исследуем функцию . Как легко установить, она убывает при всех значениях хR. Из проведенного исследования можно сделать вывод, что х=2 – единственный корень данного уравнения.
3.3 Решить уравнение
Решение: Легко проверить, что х=1 – корень данного уравнения, но мы пока не можем утверждать, что других корней нет, так как и левая и правя части уравнения – возрастающие функции. Преобразуем данное уравнение к виду . Функция в левой части – сумма двух убывающих функций, а следовательно, она также убывающая. В правой же части стоит постоянная функция. Таким образом, рассматриваемое уравнение может иметь только один корень.
3.4 Решить уравнения:
Ответы: а) х=1; б) х=0; в) х=0; г) х=2; д) х=4; е) х=5.
Рассмотренные нами примеры могли быть решены и другими методами, но традиционные методы в данных конкретных примерах достаточно трудоемки. В нашей работе мы постарались продемонстрировать применение некоторых нестандартных приемов решения уравнений, основанных на свойствах и характеристиках функций. Планируем продолжить изучение нетрадиционных и эффективных приемов решения уравнений.
http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2015/08/08/primenenie-svoystv-funktsii-pri-reshenii
http://infourok.ru/primenenie-svojstv-funkcij-dlya-resheniya-uravnenij-4185135.html