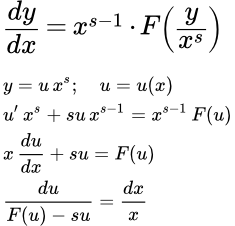Решить уравнение в обобщенных функциях

Обобщенные однородные дифференциальные уравнения первого порядка

Определение

Как определить, является ли дифференциальное уравнение обобщенным однородным

Для того, чтобы определить, является ли дифференциальное уравнение обобщенным однородным, нужно ввести постоянную t и сделать замену:
y → t α · y , x → t·x .
Если удастся выбрать такое значение α , при котором постоянная t сократится, то это – обобщенное однородное дифференциальное уравнение. Изменение производной y′ при такой замене имеет вид:
.

Пример

Определить, является ли данное уравнение обобщенным однородным:
.

Делаем замену y → t α · y , x → t·x , y′ → t α– 1 y′ :
;
.
Разделим на t α+ 5 :
;
.
Уравнение не будет содержать t , если
4 α – 6 = 0 , α = 3/2 .
Поскольку при α = 3/2 , t сократилось, то это обобщенное однородное уравнение.

Метод решения

Рассмотрим обобщенное однородное дифференциальное уравнение первого порядка:
(1) .
Покажем, что оно приводится к однородному уравнению с помощью подстановки:
t = x α .
Действительно,
.
Отсюда
; .
Подставляем в исходное уравнение (1):
;
.

Это – однородное уравнение. Оно решается подстановкой:
y = z · t ,
где z – функция от t .
При решении задач, проще сразу применять подстановку:
y = z x α ,
где z – функция от x .

Пример решения обобщенного однородного дифференциального уравнения первого порядка

Решить дифференциальное уравнение
(П.1) .

Проверим, является ли данное уравнение обобщенным однородным. Для этого в (П.1) делаем замену:
y → t α · y , x → t·x , y′ → t α– 1 y′ .
.
Разделим на t α :
.
t сократится, если положить α = – 1 . Значит – это обобщенное однородное уравнение.

Делаем подстановку:
y = z x α = z x – 1 ,
где z – функция от x .
.
Подставляем в исходное уравнение (П.1):
(П.1) ;
;
.
Умножим на x и раскрываем скобки:
;
;
.
Разделяем переменные – умножим на dx и разделим на x z 2 . При z ≠ 0 имеем:
.
Интегрируем, пользуясь таблицей интегралов:
;
;
;
.
Потенцируем:
.
Заменим постоянную e C → C и уберем знак модуля, поскольку выбор нужного знака определяется выбором знака постоянной С :
.

Возвращаемся к переменной y . Подставляем z = xy :
.
Делим на x :
(П.2) .

Когда мы делили на z 2 , мы предполагали, что z ≠ 0 . Теперь рассмотрим решение z = xy = 0 , или y = 0 .
Поскольку при y = 0 , левая часть выражения (П.2) не определена, то к полученному общему интегралу, добавим решение y = 0 .

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 03-08-2012 Изменено: 24-06-2015

Решение обыкновенных дифференциальных уравнений операторным методом в обобщенных функциях Текст научной статьи по специальности « Математика»

Похожие темы научных работ по математике , автор научной работы — В. П. Тимощенко

Текст научной работы на тему «Решение обыкновенных дифференциальных уравнений операторным методом в обобщенных функциях»

ТОМСКОГО ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ПОЛИТЕХНИЧЕСКОГО

ИНСТИТУТА имени С. М. КИРОВА

РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ОПЕРАТОРНЫМ МЕТОДОМ В ОБОБЩЕННЫХ

(Представлена научным семинаром вычислительной лаборатории ТПИ)

В работах [3, 4] строилось операторное исчисление на основе понятия обобщенной функции и разрабатывался аппарат для решения дифференциальных уравнений с постоянными коэффициентами. В настоящей работе операторный метод в обобщенных функциях распространяется на обыкновенные дифференциальные уравнения, имеющие как переменные, так и постоянные коэффициенты.

I. Множество К всех вещественных функций ф(х), каждая из которых имеет непрерывные производные всех порядков и финитна, т. е. обращается в нуль вне некоторой конечной области (зависящей от ф)г называется осноеным пространством основных финитных функций.

Последовательность основных функций ср, (х), • • ■ > ?п(х)> • ■ *

называется сходящейся к нулю в пространстве К, если эти функции обращаются в нуль вне одной и той же ограниченной области и равномерно сходятся к нулю так же, как и их производные любого порядка.

Каждый линейный непрерывный функционал, определенный на основном пространстве К, называется обобщенной функцией (см. [1], стр. 13).

Функционал, который ставит в соответствие каждой функции ф(х) ее значение в точке Хо^О, будем называть дельта-функцией и обозначать через 6(х); таким образом,

где ‘s (x) — произвольная основная функция из К; a¿ — const; pi = 0,1; ii = 0,1; gi(x) — бесконечно дифференцируемые функции; i — О, 1,2, . , л — 1.

Заметим, что для оператора Г (5, х) операции дифференцирования и умножения на функцию не перестановочны.

Сверткой /, ■■■■ fo двух обобщенных функций /х и /■> называется обобщенная функция, определяемая на любой’ основной функции ? равенством

(/. — и 0 (1) при следующих начальных данных Коши:

у(*>(0) = 0, к = 0, 1,2. п-2

Такое задание начальных условий не нарушает общности задачи Копш для уравнения (1), так как всякое уравнение порядка п, удовлетворяющее произвольным начальным данным

УФ) ‘ — Уо , К : — 0, I, 2, . , п— I,

можно с помощью некоторого преобразования свести к новому уравнению, удовлетворяющему начальным условиям (2).

Коэффициенты gi (х), . , gn-i(x) будем полагать беско-

нечно дифференцируемыми функциями, и при том некоторые из них могут быть постоянными величинами, а правую часть f(x) — непрерывной функцией на всей оси [0, сю). Решение же уравнения (I) будем искать на множестве К+ .

В операторной форме уравнение (I), с учетом условий (2), запишется следующим образом:

Если существует единственная обобщенная функция yf:K+ , удовлетворяющая уравнению (I) и условиям (2), то у будем называть решением этого уравнения и обозначать

0(,у) — I 0(,9)—I о (.у) — 1

Производя формально деление функции /, а затем ¿-функции на оператор ¿>»5) — Т (я, х), мы получим решение в виде следующего ряда: