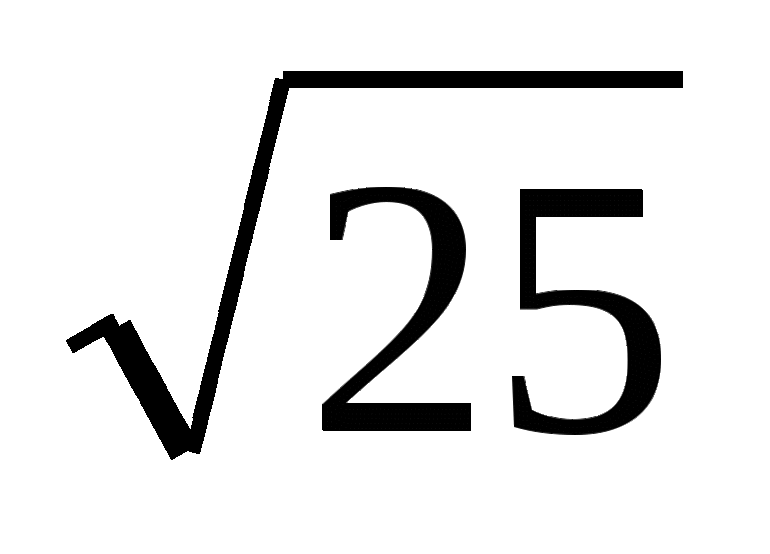Решить уравнение в зависимости от параметров

Решение показательных уравнений с параметрами

Разделы: Математика

Цели урока: Учащиеся должны знать способы решений уравнений вида – показательная функция и уметь применять при решении задач.

Ход урока.

Для первой группы учащихся выдавались следующие задания.

Для каждого значения a решить уравнения:

Задания для второй группы учащихся.

Указать число решений в зависимости от параметра а.

Третья группа решает уравнения, сводящиеся к квадратным.

Задание 1. Решить уравнение p · 4 x – 4 · 2 x + 1 = 0 и указать число решений в зависимости от параметра p.

Задание 2. При каких a уравнение 9 x + (2a + 4) · 3 x + 8a + 1 = 0 имеет единственное решение.

Задание 3. Указать число решений уравнения 49 x + 2p · 7 x + p 2 – 1 = 0 в зависимости от параметра p.

Задание 4. При каких значениях p уравнение 4 x – (5p – 3) · 2 x + 4p 2 – 3p = 0 имеет единственное решение.

Выступление первой группы – решение показательных уравнений вида

Докладывает лидер первой группы и привлекает к своему докладу участников этой группы. То есть диалог идёт ученик – ученик.

Решение исходного уравнения сводится к решению линейного уравнения с параметрами kx = b.

Если k = 0, b = 0, то 0 · x = 0, – любое действительное число.

Если k = 0, b ≠ 0, то 0 · x = b – нет решений.

Если k ≠ 0, то , один корень.

Задание 1. Решить уравнение .

Докладчик решает у доски с комментариями, остальные записывают в тетрадях.

Значит уравнение (1) можно представить в виде (a – 1)(a + 4)x = (a – 1)(a – 1)(a – 3).

Исследуем полученное уравнение:

Ответ:

На этом выступление первой группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 1.

Выступление второй группы – решение уравнений вида

Докладывает лидер второй группы и привлекает к обсуждению этого вопроса всех учащихся. Исходное уравнение равносильно уравнению ax 2 + bx + c₁ = c₀, или ax 2 + bx + c = 0.

Далее идёт диалог ученик–ученик.

1. Какое уравнение получили? – Это уравнение степени не выше второй.
2. При a = 0, bx + c = 0, получили линейное уравнение, которое может иметь одно решение, не иметь корней, или иметь бесконечное множество решений.
3. При a ≠ 0, ax 2 + bx + c = 0, квадратное уравнение.
4. От чего зависит число решений квадратного уравнения? – Число решений квадратного уравнения зависит от дискриминанта. Если D = 0 то квадратное уравнение имеет одно решение. Если D > 0, то два решения. Если D 2 + 2(a + 3)x + a + 2 = 0.

Ответ:

На этом выступление второй группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 2.

Выступление третьей группы – решение уравнений вида af 2 (x) + bf(x) + c = 0, где f(x) – показательная функция. Способ решения – введение новой переменной. f(x) = t, t > 0.

Слово предоставляется выступающему от третьей группы. Он докладывает, что их группа решала уравнения вида: (1) af 2 (x) + bf(x) + c = 0, где f(x) – показательная функция. Способ решения – введение новой переменной. f(x) = t, t > 0.

Исходное уравнение (1) равносильно

Далее докладчик задаёт вопросы, а учащиеся отвечают на них.

При каких условиях уравнение (1) имеет один корень?

1. При a = 0 уравнение (2) становится линейным, значит может иметь только один корень, и он должен быть положительным.
2. Если D = 0, уравнение (2) имеет один корень, и он должен быть положительным.
3. Если D > 0, уравнение (2) имеет два корня, но они должны быть различных знаков.
4. Если D > 0, уравнение (2) имеет два корня, но один из низ нуль. А второй положительный.

При каких условиях уравнение (1) имеет два корня?

Исходное уравнение имеет два корня, если уравнение (2) имеет два корня и оба они положительны.

При каких условиях уравнение (1) не имеет корней?

Если Dx – 4 · 2 x + 1 = 0 и указать число решений в зависимости от параметра p.

Ответим на вопрос: При каких значениях p уравнение (1) имеет один корень?

• Если одно решение. Обсуждается вопрос какие ещё могли быть варианты при t = 0 – нет решений, при t 0.

Уравнение будет иметь единственное решение при условии. Что дискриминант уравнения (2) есть число положительное, но корни при этом имеют различные знаки. Эти условия достигаются с помощью теоремы Виета. Чтобы корни квадратного трёхчлена были действительными и имели различные знаки, необходимо и достаточно выполнение соотношений.

Итак, уравнение (1) имеет единственное решение при p ≤ 0, p = 4.

Теперь остаётся ответить на вопрос. При каких условиях исходное уравнение (2) имеет два решения? Это возможно, если уравнение (2) имеет два корня и оба они положительны. По теореме Виета для того, чтобы корни квадратного трёхчлена были действительными и при этом оба были положительными, необходимо и достаточно выполнение соотношений.

Исходное уравнение имеет два корня при 0 0, то уравнение (2) имеет корни, но они оба отрицательны.

Итак, D 4. При p > 4 – нет решений. Второе условие равносильно следующим соотношениям.

Значит уравнение (1) не имеет решений при p > 4.

Ответ:

1. При p = 4, p ≤ 0 одно решение.
2. При 0 4 нет решений.

На этом выступление третьей группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 3.

Домашнее задание.

Задание 1. Найти все значения параметра a, при которых уравнение (a – 3) · 4 x – 8 · 6 x + (a +3) 9 x = 0 не имеет корней.

Задание 2.Указать число решений уравнения p · 2 x + 2 –x – 5 = 0 в зависимости от параметра p.

Задание 3. Выяснить при каких значениях a уравнение . имеет решения, найти эти решения.

Задание 4. Найти все значения p при которых уравнение (p – 1) · 4 x – 4 · 2 x + (p + 2) = 0 имеет хотя бы одно решение.

Задание 5. Указать число решений уравнения a · 12 |x| = 2 – 12 –|x| в зависимости от параметра a.

Квадратные уравнения с параметром

Уравнение называется квадратным, если имеет вид \(ax^2+bx+c=0,\) где \(a,b,c\) — любые числа \((a≠0)\). При этом надо быть внимательным, если \(a=0\), то уравнение будет линейным, а не квадратным. Поэтому, первым делом при решении квадратного уравнения с параметром, рекомендую смотреть на коэффициент при \(x^2\) и рассматривать 2 случая: \(a=0\) (линейное уравнение); \(a≠0\) (квадратное уравнение). Квадратное уравнение часто решается при помощи дискриминанта или теоремы Виета.

Исследование квадратного многочлена

Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1) Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:

• Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа \(γ\): \(x_1≤x_2 0)\); ветки параболы направлены вниз \((a 0\). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число \(γ\) должно по условию лежать вне отрезка \((x_1,x_2)\), то \(f(γ)>0\).
• \(a 0\). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа \(γ\).

В итоге получаем:

если \(a*f(γ) 0\), то \(γ∉(x_1,x_2)\).

Нам осталось наложить условие, чтобы наши корни были слева от числа \(γ\). Здесь нужно просто сравнить положение вершины нашей параболы \(x_0\) относительно \(γ\). Заметим, что вершина лежит между точками \(x_1\) и \(x_2\). Если \(x_0 0, \\x_0

При каких значениях параметра a уравнение $$a(a+3) x^2+(2a+6)x-3a-9=0$$ имеет более одного корня?

1 случай: Если \(a(a+3)=0\), то уравнение будет линейным. При \(a=0\) исходное уравнение превращается в \(6x-9=0\), корень которого \(x=1,5\). Таким образом, при \(a=0\) уравнение имеет один корень.
При \(a=-3\) получаем \(0*x^2+0*x-0=0\), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.

2 случай: Если \(a≠0; a≠-3\), то получим квадратное уравнение. При положительном дискриминанте уравнение будет иметь более одного корня: $$D>0$$ $$D/4=(a+3)^2+3a(a+3)^2>0$$ $$(a+3)^2 (3a+1)>0$$ $$a>-\frac<1><3>.$$ С учетом \(a≠0;\) \(a≠-3\), получим, что уравнение имеет два корня при \(a∈(-\frac<1><3>;0)∪(0;+∞)\). Объединив оба случая получим (внимательно прочитайте, что от нас требуется):

Найти все значения параметра a, при которых корни уравнения $$(a+1) x^2-(a^2+2a)x-a-1=0$$ принадлежат отрезку \([-2;2]\).

1 случай: Если \(a=-1\), то \(0*x^2-x+1-1=0\) отсюда \(x=0\). Это решение принадлежит \([-2;2]\).

2 случай: При \(a≠-1\), получаем квадратное уравнение, с условием, что все корни принадлежат \([-2;2]\). Для решения введем функцию \(f(x)=(a+1) x^2-(a^2+2a)x-a-1\) и запишем систему, которая задает требуемые условия:

Подставляем полученные выражения в систему:

Уравнения с параметром — алгоритмы и примеры решения

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

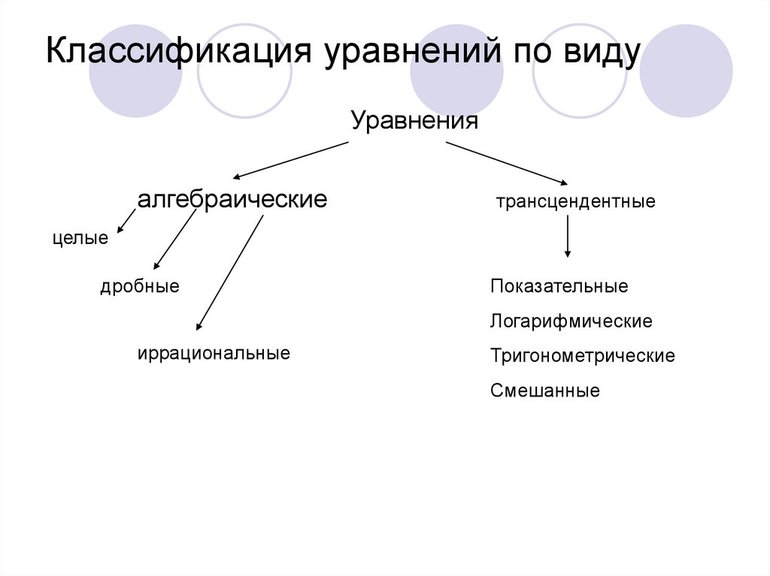
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

1. Линейные.
2. Квадратные (квадратичные).
3. Кубические.
4. Биквадратные.
5. Высших порядков.

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

Линейные и квадратичные

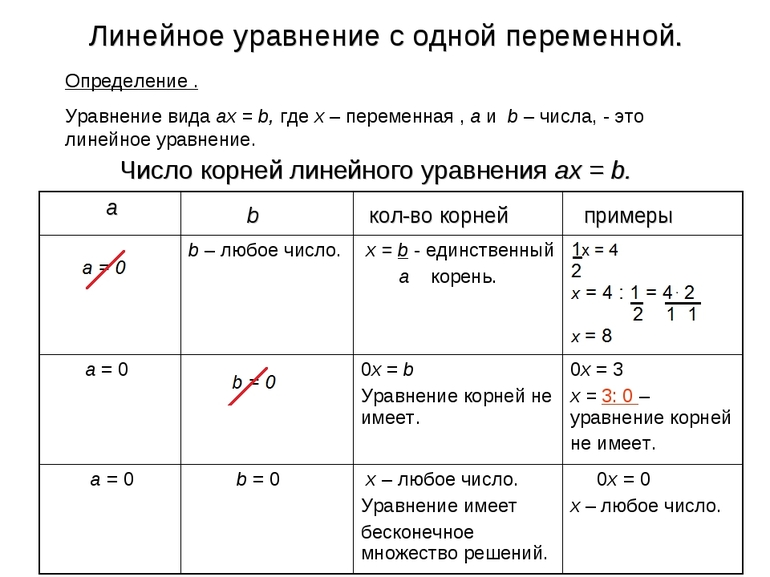
Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

1. Записывается искомое выражение.
2. При необходимости раскрываются скобки и приводятся подобные элементы.
3. Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
4. Правая часть сокращается на коэффициент при неизвестной.
5. Записывается результат.
6. Выполняется проверка посредством подстановки корня в исходное выражение.

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

1. Записать выражение.
2. Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
3. Вычислить значение D (D 0 — два решения).
4. При D=0 формула корня имеет такой вид: t=-В/(2А).
5. Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
6. Записать результат.
7. Выполнить проверку по отсеиванию ложных корней.

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

1. Приводятся подобные элементы: 3v=0.
2. Находится корень: v=0.
3. Приравнивается к выражению, которое заменяли: t 3 −2=0.
4. Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
5. Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

1. Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
2. Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
3. Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
4. Результат: m1=-3 и m2=3.
5. Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

1. Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
2. Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
3. Ввести замену v 4 −16=m: m+4p+4=0.
4. Вывести формулу нахождения параметра: р=-(m/4)-1.
5. Подставить величину m: р=-1-(v 4 +16)/4.
6. C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
7. Корни: v1=[12]^(¼) и v2=-[12]^(¼).
8. Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
9. Результат: v1=[12]^(¼).
10. Проверка: <[12]^(¼)>^4−16+4=16−16=0 (истина).

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.