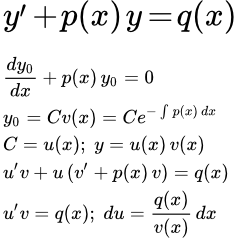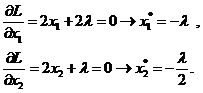Решить уравнения методом лагранжа i

Метод Лагранжа (вариации постоянной). Линейные дифференциальные уравнения первого порядка.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.

Метод вариации постоянной (Лагранжа)

В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.

Шаг 1 Решение однородного уравнения

Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные — умножаем на dx , делим на y :

Интегрируем:

Интеграл по y — табличный:

Тогда

Потенцируем:

Заменим постоянную e C на C и уберем знак модуля, что сводится к умножению на постоянную ±1 , которую включим в C :

Шаг 2 Заменим постоянную C на функцию

Теперь заменим постоянную C на функцию от x :
C → u ( x )
То есть, будем искать решение исходного уравнения (1) в виде:
(2)
Находим производную.

По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:

.
Подставляем в исходное уравнение (1):
(1) ;

.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2):
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.

Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа

Решаем однородное уравнение:

Разделяем переменные:

Умножим на :

Интегрируем:

Интегралы табличные:

Потенцируем:

Заменим постоянную e C на C и убираем знаки модуля:

Отсюда:

Заменим постоянную C на функцию от x :
C → u ( x )

Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.

Общее решение уравнения:
.

Автор: Олег Одинцов . Опубликовано: 27-07-2012 Изменено: 01-03-2015

Функция Лагранжа

Назначение сервиса . Онлайн-калькулятор используется для нахождения экстремума функции через множители Лагранжа в онлайн режиме (см. пример и пример решения графическим способом). При этом решаются следующие задачи:

составляется функция Лагранжа L(X) в виде линейной комбинации функции F(X) и ограничений g_i(x);
находятся частные производные функции Лагранжа, ∂L/∂x_i, ∂L/∂λ_i;
составляется система из (n + m) уравнений, ∂L/∂x_i = 0.
определяются переменные x_i и множители Лагранжа λ_i.

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word

Метод множителей Лагранжа применяется как в линейном программировании, так и в нелинейном. В экономике этот метод используется в задаче потребительского выбора.

Правило множителей Лагранжа

Пример 1 . Методом множителей Лагранжа решить следующую задачу оптимизации:
min f(x) = x₁ 2 + x₂ 2
h₁(x) = 2x₁ + x₂ -2 = 0
Соответствующая задача оптимизации без ограничений записывается в следующем виде:
L(x, λ) = x₁ 2 + x₂ 2 + λ(2x₁ + x₂ – 2) → min
Решение:

Для того чтобы проверить, соответствует ли стационарная точка X минимуму, вычислим матрицу Гессе функции L(x, λ), рассматриваемой как функция от x,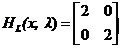
,
которая оказывается положительно определенной (2*2 – 0*0 = 4 > 0).
Это означает, что L(x, λ) – выпуклая функция. Следовательно, координаты x * = (-λ, λ/2) определяют точку глобального минимума. Оптимальное значение λ находится путем подстановки значений x₁ * и x₂ * в уравнение ограничений 2x₁ + x₂ -2 = 0, откуда вычисляем значение λ:
2λ + λ/2 = -2, откуда λ = -0.8
Таким образом, минимум достигается в точке x * с координатами x₁ * = 0.8 и x₂ * = 0.4. Значение ЦФ:
min f(x) = 0.8
Ответ: x * = [0.8; 0.4] T , f(x * ) = 0.8

Пример 2 . Исследовать на условный экстремум функцию f(x,y)_max = x 2 + 8xy+3y 2 при данных уравнениях связи.
9x +10y = 29

Уравнение Лагранжа

Вы будете перенаправлены на Автор24

Общий метод решения уравнения Лагранжа

Предположим, что некоторое дифференциальное уравнение первого порядка $F\left(x,y,y’\right)=0$, не разрешенное относительно производной, удалось разрешить относительно $y$, то есть представить в виде $y=f\left(x,y’\right)$.

Частным случаем дифференциального уравнения такого вида является уравнение Лагранжа $y=x\cdot \phi \left(y’\right)+\psi \left(y’\right)$, в котором $\phi \left(y’\right)\ne y’$.

Дифференциальное уравнение Лагранжа решают методом введения параметра $y’=p$.

При этом исходное дифференциальное уравнение можно переписать в виде $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$.

Выполнив дифференцирование по $x$ с учетом $dy=p\cdot dx$, после несложных алгебраических преобразований получаем линейное дифференциальное уравнение относительно функции $x\left(p\right)$ и её производной $\frac $, а именно: $\frac -\frac<\phi '\left(p\right)>\cdot x=\frac<\psi '\left(p\right)>$.

Это уравнение решается известным методом, в результате чего получим его общее решение $x=F\left(p,C\right)$.

Подставив полученный результат в соотношение $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$, получим $y=F\left(p,C\right)\cdot \phi \left(p\right)+\psi \left(p\right)$.

Дополнительные частные либо особые решения уравнения Лагранжа могут быть получены в результате нахождения действительных корней уравнения $p-\phi \left(p\right)=0$ и подстановки их в $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$.

Решение типичных задач

Решить дифференциальное уравнение $y=-x\cdot y’+y’^ <2>$.

Имеем дифференциальное уравнение Лагранжа, в котором $\phi \left(y’\right)=-y’$ и $\psi \left(y’\right)=y’^ <2>$.

Вводим параметр $y’=p$ и получаем $y=-x\cdot p+p^ <2>$, а также $\phi \left(p\right)=-p$ и $\psi \left(p\right)=p^ <2>$.

Теперь получим уравнение вида $\frac -\frac<\phi '\left(p\right)>\cdot x=\frac<\psi '\left(p\right)>$. Для этого находим: $\phi ‘\left(p\right)=-1$; $\psi ‘\left(p\right)=2\cdot p$; $p-\phi \left(p\right)=p-\left(-p\right)=2\cdot p$.

Уравнение приобретает вид: $\frac +\frac<1> <2\cdot p>\cdot x=1$.

Применяем алгоритм решения линейного неоднородного дифференциального уравнения:

Стандартный вид $\frac+\frac<1><2\cdot p>\cdot x=1$, где $P\left(p\right)=\frac<1><2\cdot p>$, $Q\left(p\right)=1$.
Вычисляем интеграл $I_ <1>=\int P\left(p\right)\cdot dp =\int \frac<1><2\cdot p>\cdot dp =\frac<1><2>\cdot \ln \left|p\right|$.

Выбираем для $v\left(p\right)$ простейший ненулевой вариант: $v\left(p\right)=\frac<1> <\sqrt

> $.

Вычисляем интеграл $I_ <2>=\int \frac\cdot dp =\int \sqrt

\cdot dp =\frac<2><3>\cdot p^<\frac<3><2>> $ и получаем $u\left(p,C\right)=\frac<2><3>\cdot p^<\frac<3><2>> +C$.

Получаем общее решение данного линейного неоднородного дифференциального уравнения в виде $x=\left(\frac<2><3>\cdot p^<\frac<3><2>> +C\right)\cdot \frac<1><\sqrt

> =\frac<2><3>\cdot p+\frac<\sqrt

> $.

Подставляем полученный результат в $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$. Получаем: $y=-\left(\frac<2> <3>\cdot p+\frac <\sqrt

> \right)\cdot p+p^ <2>=\frac<1> <3>\cdot p^ <2>-C\cdot \sqrt

Таким образом, общее решение данного уравнения Лагранжа в параметрической форме имеет вид: $\left\<\begin <3>\cdot p+\frac <\sqrt

> > \\ <3>\cdot p^ <2>-C\cdot \sqrt

> \end\right. $.

Для определения дополнительных частных либо особых решений находим корни уравнения $p-\phi \left(p\right)=0$: получаем $p=0$.

Подставляем $p=0$ в $y=-x\cdot p+p^ <2>$ и получаем $y=0$. Это решение является частным, так как получается из общего при $C=\frac<1> <3>\cdot p^<\frac<3> <2>> $.

Готовые работы на аналогичную тему

Решить дифференциальное уравнение $y=x\cdot y’\cdot \left(y’+2\right)$.

Имеем дифференциальное уравнение Лагранжа, в котором $\phi \left(y’\right)=y’\cdot \left(y’+2\right)$ и $\psi \left(y’\right)=0$.

Вводим параметр $y’=p$ и получаем $y=x\cdot p\cdot \left(p+2\right)$, а также $\phi \left(p\right)=p\cdot \left(p+2\right)$ и $\psi \left(p\right)=0$.

Теперь получим уравнение вида $\frac -\frac<\phi '\left(p\right)>\cdot x=\frac<\psi '\left(p\right)>$. Для этого находим: $\phi ‘\left(p\right)=2\cdot p+2$; $\psi ‘\left(p\right)=0$; $p-\phi \left(p\right)=p-\left(p^ <2>+2\cdot p\right)=-p^ <2>-p$.

Уравнение приобретает вид:

Имеем стандартный вид $x’+P\left(p\right)\cdot x=0$, где $P\left(p\right)=\frac<2>
$.
Вычисляем интеграл $I=\int P\left(p\right)\cdot dp =\int \frac<2>
\cdot dp =2\cdot \ln \left|p\right|$.
Записываем общее решение в виде $x=C\cdot e^ <-2\cdot \ln \left|p\right|>$ и выполняем упрощающие преобразования:

Подставляем полученный результат в $y=x\cdot p\cdot \left(p+2\right)$. Получаем: $y=\frac> \cdot p\cdot \left(p+2\right)$ или $y=C\cdot \left(1+\frac<2>

\right)$.

Таким образом, общее решение данного уравнения Лагранжа в параметрической форме имеет вид: $\left\<\begin > > \\

\right)> \end\right. $.

Параметр $p$ из этой системы можно исключить:

$p=\frac <\sqrt> <\pm \sqrt> $; $y=C\cdot \left(1\pm \frac <2\cdot \sqrt> <\sqrt> \right)$ — это результат решения в явной форме.

Для определения дополнительных частных либо особых решений находим корни уравнения $p-\phi \left(p\right)=-p^ <2>-p=0$.

Получаем: $p\cdot \left(p+1\right)=0$, откуда имеем два корня $p=0$ и $p=-1$.

Подставляем первый корень $p=0$ в $y=x\cdot p\cdot \left(p+2\right)$ и получаем первое дополнительное решение данного уравнения $y=0$. Это решение является частным, так как получается из общего при $C=0$.

Подставляем второй корень $p=-1$ в $y=x\cdot p\cdot \left(p+2\right)$ и получаем второе дополнительное решение данного уравнения $y=-x$. Это решение является особым, так как не получается из общего ни при каком $C$.

источники:

http://math.semestr.ru/math/lagrange.php

http://spravochnick.ru/matematika/differencialnye_uravneniya/uravnenie_lagranzha/