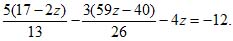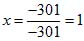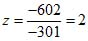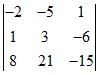Как решить уравнение определителя по математике
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Определители играют большую роль в решении систем линейных уравнений и вычислить их можно только для квадратной матрицы. Довольно часто для решения уравнений необходимо найти определитель второго и третьего порядка. Под понятием найти определитель понимают найти число. Для его нахождения используют формулы и алгоритмы. Чтобы понять логику записи определителей воспользуемся следующей схемой. Возьмём знакомую вам со школьной скамьи систему из двух уравнений с двумя неизвестными:
Исходя из данной системы, в определитель запишем коэффициенты неизвестных для каждого уравнения:
В такой вид преобразовалась наша исходная система, которую потом необходимо решить, оперируя основными методами решения квадратных матриц.
Допустим, нам необходимо вычислить определитель третьего порядка:
Руководствуясь правилом треугольников, получим:
\[\begin
Где можно решить уравнение определителя онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Решите уравнение относительно неизвестного x предварительно раскрыв определитель
После выполнения преобразований, уравнение первой степени с тремя неизвестными х, у, z примет вид
где a, b, с, d — данные числа или буквенные выражения. Одно такое уравнение, отдельно взятое, или система двух таких уравнений имеет бесчисленное множество решений. Система тpex уравнений 1-й степени с тремя неизвестными имеет в общем случае одну систему решения. В исключительных случаях (см. ниже) она может иметь бесчисленное множество или вовсе не иметь решений.
Решение системы трех уравнений с тремя неизвестными основывается на тех же приемах, что и решение системы двух уравнений с двумя неизвестными, как видно из следующего примера.
Пример. Решить систему уравнений
| 3x — 2y + 5z=7, | (1) |
| 7x + 4y — 8z = 3, | (2) |
| 5x – 3y — 4z = -12 | (3) |
Возьмем два уравнения этой системы, например (1) и (2), и будем исходить из предположения, что одно из неизвестных, например z, уже найдено, т. е. является известной величиной. Решая взятую систему относительно неизвестных х и у, найдем:
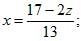
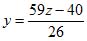
Подставив эти выражения х, у в уравнение (3), получим уравнение с одним неизвестным
Решив это уравнение, найдем z = 2. Подставив это значение в выражения (4), найдем x = 1; у = 3.
Общие формулы для решения системы
| ax + by + cz = d, | |
| a1x + b1y + c1z = d, | (5) |
| a2x + b2y + c2z = d2 |
можно получить тем же приемом. Решение будет иметь сложный и трудно запоминаемый вид, если его записать в развернутом виде, но ему можно придать легко запоминаемый и удобный для вычисления вид, если предварительно ввести понятие об определителе третьего порядка.
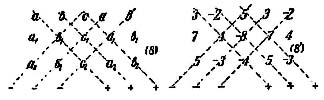
Определитель третьего порядка, сокращенно обозначаемый
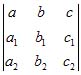
есть не что иное, как выражение
Это выражение не нужно запоминать, так как оно легко изучается из своего схематического обозначения (6) следующим образом: перепишем табличку (6), приписав к ней справа еще раз две первые ее колонны; таблица примет (8).
Проведем диагональные линии, отмеченные на схеме (8) пунктиром, и выпишем произведения букв, стоящих на каждой из шести диагональных линий. Со знаком + возьмем те три произведения, которые принадлежат диагоналям, опускающимся вправо; со знаком — остальные три произведения. Написав теперь эти произведения подряд, получим выражение (7).
Пример 1. Вычислить определитель третьего порядка
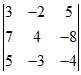
Схема (8) примет вид (8′)
Определитель (9) равен
3*4*(-4) + (-2)*(-8)*5 + 5*7*(-3) — 5*4*5 – 3*(-8)*(-3) – (- 2)*7*(-4) = -48 + 80 — 105 — 100 -72 — 56 = — 301.
С помощью определителей решение системы (5) можно подставить в виде

т.е. каждое из неизвестных равно дроби, знаменатель которой есть определитель, составленный из коэффициентов при неизвестных, а числитель получается из этого определителя заменой коэффициентов при соответствующей неизвестном на свободные члены.
Пример 2. Решить систему уравнений
3x – 2y + 5z = 7, 7x + 4y – 8z =3, 5x – 3y – 4z = -12
Общий знаменатель формул (10) вычислен в примере; он равен — 301. Числитель первой из формул (10) получаете, из (9) заменой первого его столбца столбцом свободныx членов.
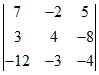
Вычисляя его по схеме (8), получим — 301. Таким образом, получаем:
Система уравнений (5) имеет единственное решение если определитель, составленный из коэффициентов при неизвестных, не равен нулю. Тогда формулы (10), в знаменателях которых стоит упомянутый определитель, решение системы (5). Если определитель, составленный из коэффициентов, равен нулю, то формулы (10) становятся непригодными для вычисления. В этом случае система (5) либо имеет бесчисленное множество решений, либо совсем их не имеет. Бесчисленное множество решений она имеет в том случае, если не только определитель, стоящий в знаменателях, но и определители, стоящие в числителях формул (10), обращаются в нуль; важно отметить, что если определитель, стоящий в знаменателях, и один из определителей, стоящих в числителях, равны нулю, то два других определителя в числителях непременно равны нулю. Наличие бесчисленного множества решений обусловливается тем, что одно из трех уравнений (5) является следствием двух других [или даже два из уравнений (5) являются каждое следствием третьего], так что фактически мы имеем несмотря лишь два (или даже одно) уравнение с тремя неизвестными.
Пример 3. В системе уравнений
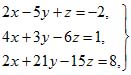
определитель из коэффициентов есть
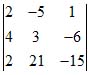
[см. схему (8)]. Взяв один из определителей, стоящих в числителях формул (10), например определитель
входящий в первую из формул (10), найдем, что он также равен нулю. Остальные два определителя, входящие во вторую и третью формулы (10), не нужно вычислять: они заведомо равны нулю. Система (11) имеет бесчисленное множество решений: одно из ее уравнений (любое) является следствием двух других. Например, если помножить второе уравнение на 2, первое на — 3 и сложить полученные уравнения, получим третье уравнение.
Система (5) вовсе не имеет решений, если определитель, стоящий в знаменателях формул (10), равен нулю, но ни один определителей, стоящих в числителях, не равен нулю. При этом достаточно убедиться, что не равен нулю один из числителей; тогда два других непременно будут не равны нулю. Отсутствие решений обусловливается тем, что одно из уравнений противоречит двум остальным (или даже каждому из них в отдельности).
Пример 4. Возьмем систему уравнений
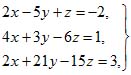
которая отличается от системы (11) только значением свободного члена в последнем уравнении. Поэтому определитель из коэффициентов остается тем же: он равен нулю. Но определители, входящие в числители, будут иными. Например, числитель первой из формул (10) будет
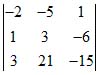
Он не равен нулю. Остальные два числителя заведомо не равны нулю. Система (12) не имеет решений. Она противоречива, ибо из первых двух уравнений вытекает как следствие уравнение 2х + 21у – 15z = =8, (см. пример 3); между тем третье уравнение системы (12) имеет вид 2х + 21у – 15z = 3, так что одно и то же выражение оказывается: равным и 3 и 8, что невозможно.
Определители, решить уравнение.
Я ПОНИМАЮ, что простейшие, но каков алгоритм его решления? просто как det A ?
не совсем понял алгоритм, не такой как мы решали без X. но у меня получились корни (16+-sqrt(304))/2 что никак не катит (
СЕРГЕЙ, ответ такой, да. а можно, пож. , форумулу по которой вышло -3 — 2х + 3х^2 + 30x — x^2 — 10x — 2x – 9 = 0
Все, понял.. у меня так же и получалось, но я не сократил на 2..
Будет
-3 — 2х + 3х^2 + 30x — x^2 — 10x — 2x – 9 = 0
2x^2+16x-12=0
x^2 + 8x — 6=0
x = -4+-кор из 22
Сокращают дроби.
Здесь левую и правую части уравнения делят на 2.
Простейшее уравнение.
Но за бесплатно никто высшую математику решать не станет.
решение: левая часть раскладывается по элементам первой строки (как при отыскании определителя) и приравнивается к 0
3*(-1-3)-x*(2-3*(x+10)) — x*(2+(x+10))=0
решаем уравнение, находим корни.
для проверки — подставляем их вместо х в определитель и считаем его значение. если получается 0, решение верно.
http://www.maths.yfa1.ru/algebra.php?id=24
http://sprashivalka.com/tqa/q/1600631