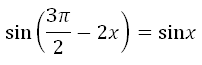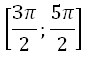Решите уравнение sin 3pi 2 2x sinx

Решить уравнение sin (3Пи/2-2x)=sinx

Здравствуйте, Дорогие друзья! В данной статье мы с вами рассмотрим решение тригонометрического уравнения, и найдём корни принадлежащие определённому (заданному) отрезку. Подобный пример мы уже рассмотрели в предыдущей статье данной рубрики. Но в этом примере мы разберём другой способ определения корней на отрезке.

а) Решите уравнение.
б) Укажите корни уравнения, принадлежащие отрезку

а) Используем формулу приведения для синуса и формулу косинуса двойного угла:

Привели уравнение к квадратному. Производим замену переменной, обозначим sin x = t.

Решая квадратное уравнение 2t 2 – t – 1 = 0, получим:

Решая sin x = 1, получим:

Решая sin x = –½, получим:

Итак, мы получили корни:

б) С помощью единичной окружности отберём корни на отрезке

Без расчётов, визуально сходу определить корни принадлежащие отрезку может далеко не каждый. Для этого необходима большая практика и отличное «понимание» тригонометрической окружности. Рассмотрим способ, при использовании которого, вы безошибочно определите корни на заданном интервале. Переведём радианы в градусы . Так как Пи радиан это 180 градусов, то отрезок

в (градусах) будет выглядеть следующим образом: [270 0 ;450 0 ]. Отберём корни.

Суть подхода такова: мы берём произвольные коэффициенты k, подставляем в каждый из корней и вычисляем. Получаем корни (углы) и смотрим – попадают ли они в интервал. Те, которые попадают мы отмечаем как верный ответ.

При k = 3 и далее можно не проверять, так как уже видно, что при этом значении k углы будут находиться вне пределов интервала.

Таким образом, отрезку [270 0 ;450 0 ] принадлежат корни 450 0 и 330 0 в радианах это

Возникает вопрос: какие «произвольные» коэффициенты k брать?

Ответ прост: в пределах от –3 до 3, так как границы заданного интервала в подобных заданиях обычно лежат «недалеко» от нуля. Для начала берите k = 0, затем по полученным значениям корней поймете какие коэффициенты брать, положительные или отрицательные.

Конечно, данный способ совершенным не назовёшь, кому-то наиболее понятен подход изложенный в уже указанной выше статье. Но он, безусловно, позволяет находить верное решение. Да и в градусной мере оценивать принадлежность угла указанному интервалу многим удобнее.

Кстати, если сравнивать объём вычислений представленного способа и описанного в уже указанной статье (см. ссылку выше), то он практически одинаков.

На этой странице вы можете посмотреть примеры уравнений.

Задача 9281 Решить уравнение:2sin(3pi/2 — x)*sin(x -.

Условие

Решить уравнение:2sin(3pi/2 — x)*sin(x — pi) + sqrt(2)*cosx=0
Отобрать значения на промежутке : [-5pi/2;7pi/2]

Решение

2sin(3π/2 – x)·sin(x – π) + √2·cosx=0.
По формулам приведения
sin(3π/2 – x)=-cosx;
sin(x-π)=-sin(π-x)=-sinx.
Уравнение принимает вид:
2·(-cosx)·(-sinx)+√2·cosx=0;
√2·cosx·(√2·sinx+1)=0;
1)cosx=0⇒ x=(π/2)+πk, k∈Z.
или
2)sinx=-√2/2⇒ x=(-π/4)+2πn, n∈Z или x=(-3π/4)+2πm,m∈Z.

С помощью неравенств определим, какие корни принадлежат отрезку [–5π/2;7π/2]
1)
–5π/2≤(π/2)+πk≤7π/2, k∈Z;
-5/2≤(1/2)+k≤7/2, k∈Z;
(-5/2)-(1/2)≤k≤(7/2)-(1/2), k∈Z;
-3≤k≤2,k∈Z;
при k=-3 получаем корень (π/2)+π·(-3)=-5π/2;
при k=-2 получаем корень (π/2)+π·(-2)=-3π/2;
при k=-1 получаем корень (π/2)+π·(-1)=-π/2;
при k=0 получаем корень (π/2)+π·0=π/2;
при k=1 получаем корень (π/2)+π·1=3π/2;
при k=2 получаем корень (π/2)+π·2=π/2.

Указанному промежутку принадлежат корни:
(-5π/2); (-3π/2);(-π/2);(π/2);(3π/2);(5π/2);(7π/2)

при n=-1 получаем корень (-π/4)+2π·(-1)=-9π/4;
при n=0 получаем корень (-π/4)+2π·0=-π/4;
при n=1 получаем корень (-π/4)+2π·1=7π/4;
Указанному промежутку принадлежат корни:
(-9π/4);(-π/4);(7π/4).

при m=0 получаем корень (-3π/4)+2π·0=-3π/4;
при m=1 получаем корень (-3π/4)+2π·1=5π/4;
при m=2 получаем корень (-3π/4)+2π·2=13π/4;
Указанному промежутку принадлежат корни:
(-3π/4);(5π/4);(13π/4);.
О т в е т.
a)(π/2)+πk;(-π/4)+2πn;(-3π/4)+2πm;k;n;m∈Z.

б)(-5π/2);(-9π/4); (-3π/2);(-3π/4);(-π/2);(-π/4);(π/2);(5π/4);(3π/2);(7π/4);(5π/2);(13π/4);(7π/2)- корни уравнения, принадлежащие отрезку [–5π/2;7π/2]

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение тригонометрических уравнений.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое уравнение
Решить уравнение

Немного теории.

Тригонометрические уравнения

Уравнение cos(х) = а

Из определения косинуса следует, что \( -1 \leqslant \cos \alpha \leqslant 1 \). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.

Уравнение cos x = а, где \( |a| \leqslant 1 \), имеет на отрезке \( 0 \leqslant x \leqslant \pi \) только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если a

Уравнение sin(х) = а

Из определения синуса следует, что \( -1 \leqslant \sin \alpha \leqslant 1 \). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.

Уравнение sin х = а, где \( |a| \leqslant 1 \), на отрезке \( \left[ -\frac<\pi><2>; \; \frac<\pi> <2>\right] \) имеет только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если а

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Уравнение tg x = а для любого a имеет на интервале \( \left( -\frac<\pi><2>; \; \frac<\pi> <2>\right) \) только один корень. Если \( |a| \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right) \); если а

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Уравнения, сводящиеся к квадратным

Решить уравнение 2 cos 2 (х) — 5 sin(х) + 1 = 0

Заменяя cos 2 (х) на 1 — sin 2 (х), получаем
2 (1 — sin 2 (х)) — 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y — 3 = 0, откуда y₁ = -3, y₂ = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; \( x = (-1)^n \text(0,5) + \pi n = (-1)^n \frac<\pi> <6>+ \pi n, \; n \in \mathbb \)
Ответ \( x = (-1)^n \frac<\pi> <6>+ \pi n, \; n \in \mathbb \)

Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) — 4 = 0

Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin 2 (6х)) + 4 sin(6х) — 4 = 0 => 3 sin 2 (6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 — 4y +1 =0, откуда y₁ = 1, y₂ = 1/3

Уравнение вида a sin(x) + b cos(x) = c

Решить уравнение 2 sin(x) + cos(x) — 2 = 0

Используя формулы \( \sin(x) = 2\sin\frac <2>\cos\frac<2>, \; \cos(x) = \cos^2 \frac <2>-\sin^2 \frac <2>\) и записывая правую часть уравпения в виде \( 2 = 2 \cdot 1 = 2 \left( \sin^2 \frac <2>+ \cos^2 \frac <2>\right) \) получаем

Поделив это уравнение на \( \cos^2 \frac <2>\) получим равносильное уравнение \( 3 \text^2\frac <2>— 4 \text\frac <2>+1 = 0 \)
Обозначая \( \text\frac <2>= y \) получаем уравнение 3y 2 — 4y + 1 = 0, откуда y₁=1, y₁= 1/3

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях \( a \neq 0, \; b \neq 0, \; c \neq 0, \; c^2 \leqslant b^2+c^2 \) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на \( \sqrt \):

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, \( \sqrt = 5 \). Поделим обе части уравнения на 5:

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0

Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0

Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) — sin 2 (x), то
cos(2x) = 1 — sin 2 (x) — sin 2 (x), cos(2x) = 1 — 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0