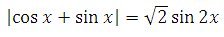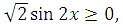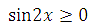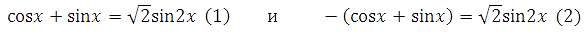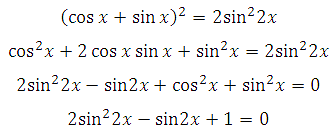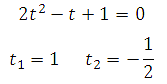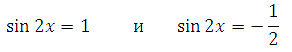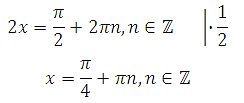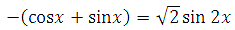Решите уравнение sin2x модуль sinx

Решить |cosx+sinx|=(sqrt2) sin2x

1. Сразу следует отметить, что выражение

так как |cos x+sin x| имеет неотрицательное значение. Исходя из того, что корень из двух есть число положительное, получаем:

2. Используя свойство модуля, получим два уравнения, решения каждого из них будут являться решением данного уравнения:

Решаем первое. Возводим в квадрат обе части:

Данное уравнение сводится к квадратному . Пусть sin2x = t, тогда получим

Мы установили (в начале решения), что sin2x ≥ 0. Это область допустимых значений. Можем сделать вывод, что второе уравнение решать нет смысла – так как полученные при решении значения х не будут входить в область определения.

Решаем sin2x = 1, получим:

Рассмотрим второе уравнение:

Решением является тот же корень что и при решении уравнения (1), так как при возведении в квадрат обеих частей получим то же уравнение

Тригонометрические уравнения с модулем

Разделы: Математика

Раскрытие модуля по определению

Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а 2 x-sinx=0

sinx=0 или sinx= (оба уравнения удовлетворяют условию sinx≥0)

Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx 2

cosx=0 или x+1,5=1 или x-1,5 = -1

х= -0,5 х = -2,5

Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)

Ответ:

№5. Найти все решения уравнения на отрезке [0;4].

Решение. Перепишем уравнение в виде

Раскрывая знак модуля, получаем системы:

Решая первую систему, получим

Из серии в нужном промежутке [0;4] лежат точки 0 и ; , а из серии

Решая вторую систему, получим систему , которая не имеет решений.

Ответ:

№6 Решить уравнение.

Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия правого модуля по определению рассматривается только один случай:

х=2

Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2

№7. Решить уравнение.

Решение. ОДЗ:

Раскрывая знак модуля, получаем системы:

Решая первую систему, получим cos2x=0, и из решений надо выбрать те, при которых sinx>0. На круге видно, что это точки вида

Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.

Ответ:

№8. Решить уравнение.

Решение. Преобразуем уравнение следующим образом:

Ответ:

№9. Решить уравнение.

Решение. Выражение под первым модулем всегда неотрицательно, и его можно сразу отбросить. Второй модуль раскрываем по определению.

Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x 2 +15x-45=(-x 2 +15x-44)-1≤-1

при причем, f(х)= -1 в точках 4 и 11.Левая часть cos при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.

При решении уравнения второй системы получается:

В промежутке только одно целое нечетное число 3, т.е

Другие способы раскрытия модулей.

Уравнения вида можно решать и следующим способом:

№10. Решить уравнение.

Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx 21.02.2008

sin^2x+sinx-2=0 (уравнение)

Найду корень уравнения: sin^2x+sinx-2=0

Решение

Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_ <1>= \frac <\sqrt— b><2 a>$$
$$w_ <2>= \frac <- \sqrt— b><2 a>$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 1$$
$$c = -2$$
, то

Т.к. D > 0, то уравнение имеет два корня.

или
$$w_ <1>= 1$$
$$w_ <2>= -2$$
делаем обратную замену
$$\sin <\left(x \right)>= w$$
Дано уравнение
$$\sin <\left(x \right)>= w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = 2 \pi n + \operatorname<\left(w \right)>$$
$$x = 2 \pi n — \operatorname <\left(w \right)>+ \pi$$
Или
$$x = 2 \pi n + \operatorname<\left(w \right)>$$
$$x = 2 \pi n — \operatorname <\left(w \right)>+ \pi$$
, где n — любое целое число
подставляем w:
$$x_ <1>= 2 \pi n + \operatorname <\left(w_<1>\right)>$$
$$x_ <1>= 2 \pi n + \operatorname<\left(1 \right)>$$
$$x_ <1>= 2 \pi n + \frac<\pi><2>$$
$$x_ <2>= 2 \pi n + \operatorname <\left(w_<2>\right)>$$
$$x_ <2>= 2 \pi n + \operatorname<\left(-2 \right)>$$
$$x_ <2>= 2 \pi n — \operatorname<\left(2 \right)>$$
$$x_ <3>= 2 \pi n — \operatorname <\left(w_<1>\right)> + \pi$$
$$x_ <3>= 2 \pi n — \operatorname <\left(1 \right)>+ \pi$$
$$x_ <3>= 2 \pi n + \frac<\pi><2>$$
$$x_ <4>= 2 \pi n — \operatorname <\left(w_<2>\right)> + \pi$$
$$x_ <4>= 2 \pi n + \pi — \operatorname<\left(-2 \right)>$$
$$x_ <4>= 2 \pi n + \pi + \operatorname<\left(2 \right)>$$