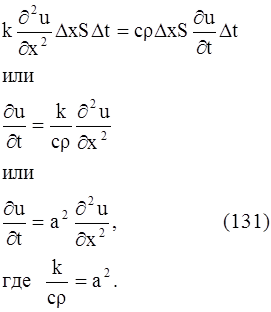Преобразование Фурье с примерами решения и образцами выполнения
Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.
Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(х) называется функция (*)
где К(х, w) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).
Интеграл Фурье
Всякая функция f(x), которая на отрезке [— l, l] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом (1)
Коэффициенты аn и bn ряда (1) определяются по формулам Эйлера—Фурье:
(2)
Ряд в правой части равенства (1) можно записать в иной форме. С этой целью внесем в него из формул (2) значения коэффициентов аn и bn, подведем под знаки интегралов cos 
(3)
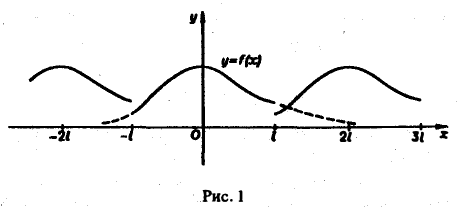
Если функция f(x) первоначально была определена на интервале числовой оси, большем, чем отрезок [-l, l] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-l, l] и продолжит ее на всю числовую ось как периодическую функцию с периодом 2l (рис. 1).
Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при l → +∞. При этом естественно потребовать выполнения следующих условий:
1, f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;
2. функция f(x) абсолютно интегрируема на всей числовой оси,
При выполнении условия 2 первое слагаемое правой части равенства (3) при l → +∞ стремится к нулю. В самом деле,
Попытаемся установить, во что перейдет в пределе при l → +∞ сумма в правой части (3). Положим
так, что 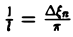
В силу абсолютной сходимости интеграла эта сумма при больших l мало отличается от выражения
которое напоминает интегральную сумму для функции переменного ξ
составленную для интервала (0, + ∞) изменения Поэтому естественно ожидать, что при l → +∞ ( 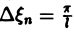
С другой стороны, при l → +∞ (х фиксировано) из формулы (3) вытекает, что
и мы получаем равенство
(7)
Достаточное условие справедливости формулы (7) выражается следующей теоремой.
Теорема:
Если функция f(x) абсолютно интегрируема на всей числовой оси — ∞
При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции f(x), значение интеграла в правой части (7) равно
Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралам Фурье.
Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде (8)
Функции а( ξ ), b( ξ ) являются аналогами соответствующих коэффициентов Фурье an и bn 2π-периодической функции, но последние определены для дискретных значений п, в то время как а( ξ ), b( ξ ) определены для непрерывных значений ξ ∈ (— ∞, + ∞).
Комплексная форма интеграла Фурье
Предполагая f(x) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл
Этот интеграл равномерно сходится для — ∞
и потому представляет собой непрерывную и, очевидно, нечетную функцию от ξ. Но тогда
С другой стороны, интеграл
есть четная функция переменной так что
Поэтому интегральную формулу Фурье можно записать так:
на мнимую единицу i и прибавим к равенству (10). Получим
откуда, в силу формулы Эйлера (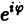
(11)
Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по ξ понимается в смысле главного значения по Коши:
Преобразование Фурье. Косинус- и синус-преобразования Фурье
Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.
Определение:
называется преобразованием Фурье функции f(x) (спектральной функцией).
Это — интегральное преобразование функции f(x) на интервале (- ∞ ,+ ∞) с ядром
Используя интегральную формулу Фурье
Это так называемое обратное преобразование Фурье, дающее переход от F( ξ ) к f(x). Иногда прямое преобразование Фурье задают так:
Тогда обратное преобразование Фурье определится формулой
Преобразование Фурье F( ξ ) функции f(х) определяют также следующим образом:
Тогда, в свою очередь,
При этом положение множителя 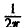
Пример:
Найти преобразование Фурье функции
Это равенство допускает дифференцирование по ξ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда ξ принадлежит любому конечному отрезку):
Интегрируя по частям, будем иметь
Внеинтегральное слагаемое обращается в нуль, и мы получаем
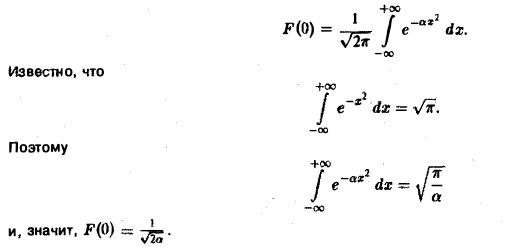
(С — постоянная интегрирования). Полагая в (4) ξ = 0, найдем С —F(0). В силу (3) имеем
В частности, для
Пример:
Разряд конденсатора через сопротивление. Рассмотрим функцию
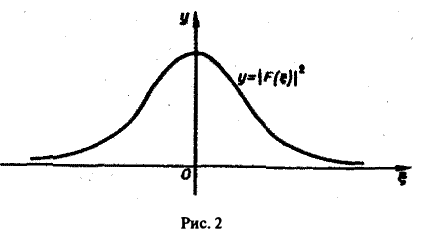
Для спектральной функции F( ξ ) получаем
Условие абсолютной интегрируемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как f(x) = 1. f(x) = x 3 , f(х) = cosx, f(х) = е х , для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.
Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| → + ∞ (как в примерах 1 и 2).
Косинус- и синус-преобразования Фурье
Используя формулу косинуса, разности, перепишем интегральную формулу Фурье
в следующем виде:
Пусть f(x) — четная функция. Тогда
так что из равенства (5) имеем
(6)
В случае нечетной f(x) аналогично получаем
(7)
Если f(х) задана лишь на (0, + ∞), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным.
Определение:
называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x)
Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc( ξ ). Иными словами, функции f и Fc являются взаимными косинус-преобразованиями.
Определение:
называется синус-преобразованием Фурье функции f(x).
Из (7) получаем, что для нечетной функции f(х)
т.е. f и Fs являются взаимными синус-преобразованиями.
Пример:
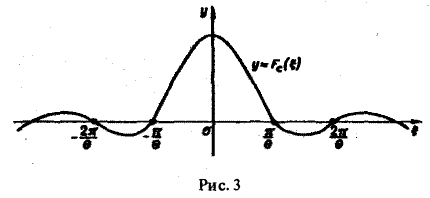
Прямоугольный импульс. Пусть f(t) — четнaя функция, определенная следующим образом:
Воспользуемся полученным результатом для вычисления интеграла
В силу формулы (9) имеем
В точке t = 0 функция f(t) непрерывна и равна единице.
Поэтому из (12′) получим
Амплитудный и фазовый спектры интеграла Фурье
Пусть периодическая с периодом 2π функция f(х) разлагается в ряд Фурье
Это равенство можно записать в виде
где Cn = 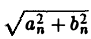
Для непериодической функции f(x), заданной на (- ∞, + ∞), при определенных условиях оказывается возможным представить ее интегралом Фурье
осуществляющим разложение этой функции по всем частотам 0
(прямое преобразование Фурье функции f(х)).
называется амплитудным спектром, а функция
(0 — фазовым спектром функции f(x).
Амплитудный спектр A (ξ) служит мерой вклада частоты ξ в функцию f(х).
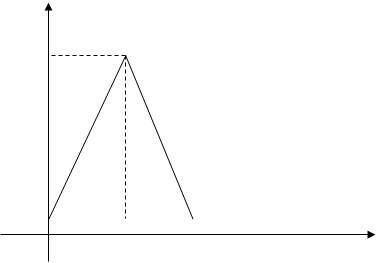
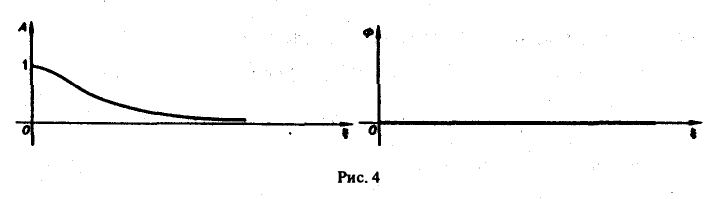
Пример:
Найти амплитудный и фазовый спектры функции
Находим спектральную функцию
Графики этих функций изображены на рис. 4.
Свойства преобразования Фурье
1, Линейность. Если F( ξ ) и G( ξ ) — преобразования Фурье функций f(х) и g(х) соответственно, то при любых постоянных а и β преобразованием Фурье функции а f(х) + β g(х) будет функция a F( ξ ) + βG( ξ ).
Пользуясь свойством линейности интеграла, имеем
Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через 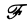
Если F( ξ ) есть преобразование Фурье абсолютно интегрируемой на всей числовой оси функции f(х), то F( ξ ) ограничена при всех ξ ∈ (— ∞, + ∞).
Пусть функция f(х) абсолютно интегрируема на всей оси — ∞
— преобразование Фурье функции f(х). Тогда
Задача:
Пусть f(x) — функция, допускающая преобразование Фурье, h — действительное число. Функция fh(x) = f(x-h) называется сдвигом функции f(x). Пользуясь определением преобразования Фурье, показать, что
Задача:
Пусть функция f(x) имеет преобразование Фурье F( ξ ), h — действительное число. Показать, что
3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция f(х) имеет производную f'(х), также абсолютно интегрируемую на всей оси Ох, так что f(х) стремится к нулю при |х| —► + ∞. Считая f'(х) гладкой функцией, запишем
Интегрируя по частям, будем иметь
Внеинтегральное слагаемое обращается в нуль (так как f(х) → 0 при |х| → + ∞), и мы получаем (1)
Таким образом, дифференцированию функции f(х) отвечает умножение ее образа Фурье 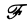
Если функция f(х) имеет гладкие абсолютно интегрируемые производные до порядка m включительно и все они, как и сама функция f(х), стремятся к нулю при |x| → + ∞, то, интегрируя по частям нужное число раз, получим
Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину iξ и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.
Так как преобразование Фурье 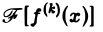
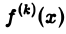
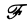
Из этой оценки следует: чем больше функция f(х) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при | ξ | → + ∞.
Замечание:
Условие 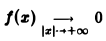
4. Связь между скоростью убывания функции f(x) при |х| → + ∞ и гладкостью ее преобразования Фурье. Предположим, что не только f(x), но и ее произведение хf(х) является абсолютно интегрируемой функцией на всей оси Ох. Тогда преобразование Фурье
функции f(x) будет дифференцируемой функцией.
Действительно, формальное дифференцирование по параметру ξ подынтегральной функции приводит к интегралу
который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и
т. е. операция умножения f(х) на аргумент х переходит после преобразования Фурье в операцию
Если вместе с функцией f(х) абсолютно интегрируемыми на всей оси Ох являются функции хf(х)…..х m f(х), то процесс дифференцирования можно продолжить.
Получим, что функция F( ξ ) = 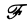
Таким образом, чем быстрее функция f(х) убывает при |х| → + ∞, тем более гладкой получается функция F( ξ ) = 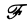
Теорема:
О свертке. Пусть F1( ξ ) и F2( ξ ) — преобразования Фурье функций f1(x) и f2(x) соответственно. Тогда
причем двойной интеграл в правой части сходится абсолютно.
Положим х + у = т, так что у = т — х. Тогда будем иметь
или, меняя порядок интегрирования,
называется сверткой функций f(x) и f2(x) и обозначается символом 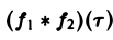
Отсюда видно, что преобразование Фурье свертки функций f1(x) и f2(x) равно умноженному на 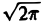
Замечание:
Нетрудно установить следующие свойства свертки:
Приложения преобразования Фурье
1, Пусть 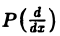
(аo, a1,… ,ат = const). Используя формулу для преобразования Фурье производных функции у(х), находим
Рассмотрим дифференциальное уравнение
где 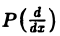
Предположим, что искомое решение у(х) имеет преобразование Фурье y(ξ), а функция f(x) имеет преобразование f( ξ ). Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси Oξ относительно y(ξ)
так что формально
где символ 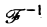
Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида
Они не являются абсолютно интегрируемыми на оси — ∞
(а = const), при начальных условиях
Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение φ(х) точек струны, а начальные скорости отсутствуют.
Поскольку пространственная переменная х изменяется в пределах от — ∞ до + ∞, подвергнем уравнение и начальные условия преобразованию Фурье по переменной х. Будем предполагать, что
1) функции u(z, t) и φ(x) — достаточно гладкие и стремятся к нулю при \х\ → + ∞ и ∀t ≥ О настолько быстро, что существуют преобразования Фурье
2) допустимы операции дифференцирования, так что
Умножая обе части (2) на 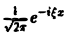
а из начальных условий (3) найдем
Таким образом, применяя к задаче (2)-(3) преобразование Фурье, приходим к задаче Коши (8)—(10) для обыкновенного дифференциального уравнения, где ξ — параметр. Решением уравнения (8) является функция
Из условий (9) и (10) находим, что С1( ξ ) = φ( ξ ). C2( ξ ) = 0, так что v( ξ, t) = φ( ξ )cos aξt. Применяя обратное преобразование Фурье, получим
Это частный случай формулы Даламбера решения задачи (2)-(3).
2. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т. е. уравнений, в которых неизвестная функция входит под знак интеграла.
Рассмотрим, например, уравнение
где φ(х) — искомая функция. Записав (1) в виде
замечаем, что левую часть (2) можно рассматривать как преобразование Фурье функции φ(х), так что (2) равносильно следующему равенству:
Тогда по формуле обращения
Функция 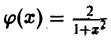
Понятие о многомерном преобразовании Фурье
Преобразование Фурье:
Многомерным преобразованием Фурье абсолютно интегрируемой функции f(х1, х2,…, хb) называется функция
символ 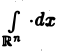
Свойства многомерного преобразования аналогичны соответствующим свойствам преобразования Фурье функции одной переменной. В специальном случае, когда
Дополнение к преобразованию Фурье


Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Реферат: Ряды Фурье и их приложения
| Название: Ряды Фурье и их приложения Раздел: Рефераты по математике Тип: реферат Добавлен 15:46:46 03 августа 2005 Похожие работы Просмотров: 14201 Комментариев: 22 Оценило: 12 человек Средний балл: 4.8 Оценка: 5 Скачать |
 |
При любом натуральном n
и, следовательно, эта последовательность функций, хотя и сходится к нулю при n → ∞, но неравномерно. Между тем
т. е. последовательность функций
Из элементов некоторой последовательности функций ƒ1 , ƒ2 , ƒ3 ,… (принадлежащих 
Сумма первых его n членов
есть функция, принадлежащая к 
то говорят, что ряд (12) сходится к функции ƒ в смысле среднего квадратического и пишут
Можно рассматривать пространство 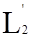
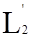
а норма ƒ определяется как величина
2.1. Интегралы от периодических функций.
Пусть ƒ(x) – периодическая функция, с периодом Т, интегрируемая на любом сегменте вида [х0 , х0 +Т]. Тогда величина интеграла 
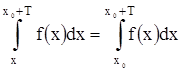
2.2. Интегралы от некоторых тригонометрических 
Укажем значения некоторых интегралов:
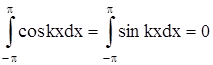
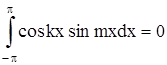
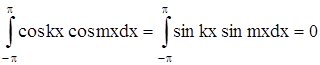
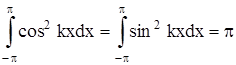
Теперь можем вычислить коэффициенты Фурье ak и bk ряда (2). Для разыскания коэффициента an при каком-либо определенном значении n≠0 умножим обе части равенства (2) на cosnx и произведя математические операции в пределах от –π до π, получим:
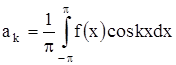
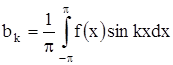

В некоторых случаях, для более узких классов функций, формулы (17), (18) были известны ещё Эйлеру. Таким образом, эти формулы ещё называют формулами Эйлера-Фурье.
Обратим внимание, что постоянная 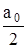
Вышеприведенные соображения показывают, что поиски тригонометрического разложения данной функции целесообразно начать с изучения её ряда Фурье, откладывая на потом строгое изучение вопроса о том, для каких функций ряд сходится, и притом именно к данной функции. Пока же этого не сделано, функции ƒ(x) сопоставляют её формальный ряд Фурье, что обычно записывают в виде:

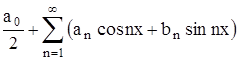
про который известно, что его коэффициенты вычислены по функции ƒ(x) по формулам Эйлера – Фурье (4), (17) и (18), но ничего не утверждается о его сходимости и тем более – о его сходимости к данной функции.
Из определения ряда Фурье не следует, что функция должна в него разлагаться. Из сказанного выше следует только, что некоторая функция допускает разложение в равномерно сходящийся ряд вида (19), то этот ряд будет её рядом Фурье.
3. Признаки сходимости 
Зададим вопрос: какими свойствами должна обладать функция, чтобы построенный, для неё ряд Фурье сходился и чтобы сумма построенного ряда Фурье равнялась значениям данной функции в соответствующих точках?
Сформулируем теорему, которая даст достаточные условия представимости функции ƒ(x) рядом Фурье. (из Пискунова)
Определение. Функция ƒ(x) называется кусочно- монотонной на отрезке [a, b], если этот отрезок можно разбить конечным числом точек х1 , х2 , …,хn-1 на интервалы (а, х1 ), (х1 , х2 ),…, (хn-1 , b) так, что на каждом из интервалов функция монотонна, т. е. либо не возрастающая, либо неубывающая.
Если периодическая функция ƒ(x) с периодом 2π – кусочно монотонная и ограниченная на отрезке [-π, π], то ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда s(x) равна значению функции ƒ(x) в точках непрерывности функции. В точках разрыва функции ƒ(x) сумма ряда равняется среднему арифметическому пределов функции ƒ(x)справа и слева, т. е. если х = с – точка разрыва функции ƒ(x), то
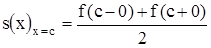
Из этой теоремы следует, что класс функций, представимых рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных отделах математики. Особенно успешно ряды Фурье применяются в математической физике и её приложениях к конкретным задачам механики и физики.
Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс высшей математики», Шнейдер и др., стр. 181)
При выводе формул (4), (17), (18) мы заранее предполагали, что функция ƒ(x) разлагается в правильно сходящийся тригонометрический ряд (1). Если же такого предположения не делать, а допустить, что для функции ƒ(x) существуют все интервалы, стоящие в правых частях формул (4), (17), (18), то по этим формулам можно вычислить коэффициенты a0, ak и bk и составить тригонометрический ряд (1), который представляет собой ряд Фурье, соответствующий данной функции.
Является ли построенный таким образом ряд Фурье сходящимся и если он сходится, то имеем ли мы право утверждать, что он сходится именно к функции ƒ(x), с помощью которой вычислялись коэффициенты ряда?
Оказывается, что сходимость ряда Фурье к заданной функции имеет место для довольно широкого класса функций. Достаточные условия сходимости ряда Фурье, и, следовательно, возможность разложения функций в ряд Фурье даются теоремой Дирихле. Прежде чем формулировать эту теорему, введем два определения.
Функция ƒ(x) называется кусочно-монотонной на сегменте [a, b], если этот сегмент можно разделить на конечное число сегментов, внутри каждого, из которых функция либо только возрастает, либо только убывает, либо постоянна.
Основное определение. Функция ƒ(x) называется удовлетворяющей условиям Дирихле на сегменте [ a, b], если:
1)функция непрерывна на сегменте [ a, b] или же имеет
на нем конечное число точек разрыва 1 рода;
2) функция кусочно-монотонна на сегменте [ a, b].
3.1. Примеры разложения функций в ряды Фурье.
Пример 1. Периодическая функция ƒ(x) с периодом 2π определяется следующим образом: ƒ(x) = х , -π ′ . На концах этого элемента, по касательным к струне, действуют силы Т.
(Н.С. Пискунов стр. 246, рис. 372)
Пусть касательные образуют с осью Ох углы φ и φ + ∆φ. Тогда проекция на ось Ou сил, действующих на элемент ММ ′ , будет равна T· sin (φ + ∆φ) – sin φ . Так как угол φ мал, то можно положить tg φ ≈ sin φ, мы будем иметь:
T sin (φ + ∆φ) – T sin φ ≈ T tg (φ + ∆φ) – T tg φ =
(здесь мы применили теорему Лагранжа к выражению, стоящего в квадратных скобках).
Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть ρ – линейная плотность струны. Тогда масса элемента струны будет ρ ∆х. Ускорение элемента равно ∂ 2 u / ∂t 2 . Следовательно, по принципу Даламбера будем иметь:
Сокращая на ∆х и обозначая a 2 = T/ ρ, получаем уравнение движения
Это и есть волновое уравнение – уравнение колебаний струны. Для полного определения движения струны одного уравнения (35) недостаточно. Искомая функция u(x, t) должна удовлетворять ещё граничным условиям , указывающих, что делается на концах струны (х = 0 и х = ℓ), и начальным условиям , описывающим состояние струны в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.
Пусть, например, как мы предполагали, концы струны при х = 0 и х = ℓ неподвижны. Тогда при любом t должны выполняться равенства:
Эти равенства являются граничными условиями для нашей задачи.
В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией ƒ(x). Таким образом, должно быть
u (x, 0) = u |t = 0 = ƒ(x). (37)
Далее в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией φ(х):
Условия (101 , ) и (101 , , ) являются начальными условиями.
Замечание. В частности, может быть, ƒ(x) ≡ 0 или φ(x) ≡ 0. Если же ƒ(x) ≡ 0 и φ(x) ≡ 0, то струна будет находиться в покое, следовательно, u (x, t) ≡ 0.
Как указывалось выше, к уравнению (30) приводит и задача об электрических колебаниях в проводах. Покажем это. Электрический ток в проводе характеризуется величиной ί(x, t) и напряжением υ(x, t), которые зависят от координаты х точки провода и от времени t. Рассматривая элемент провода ∆х, можем написать, что падение напряжения на элементе ∆х равно
Это падение напряжения складывается из омического, равного ίR∆x, и индуктивного , равного (∂ ί /∂ t )L∆x. Итак,
где R и L — сопротивление и коэффициент самоиндукции, рассчитанный на единицу длины провода. Знак минус взят потому, что ток течет в направлении, обратном возрастанию υ. Сокращая на ∆х, получаем уравнение
Далее, разность токов, выходящих из элемента ∆х и выходящего из него время ∆t, будет
Она расходуется на зарядку элемента, равную C∆x (∂υ/∂t) ∆t, и на утечку через боковую поверхность провода вследствие несовершенства изоляции, равную Аυ∆х∆t (здесь А – коэффициент утечки). Приравнивая эти выражения и сокращая на ∆x∆t, получим уравнение:
Уравнения (103) и (104) принято называть телеграфными уравнениями.
Из системы уравнений (103) и (104) можно получить уравнение, содержащую только искомую функцию ί(x, t), и уравнение, содержащее только искомую функцию υ (x, t). Продифференцируем члены уравнения (104) по х; члены уравнения (103) продифференцируем по t и умножим их на С. Произведя вычитание, получим:
Подставляя в последнее уравнение выражение (∂υ /∂х) из уравнения (103), получим:
Аналогичным образом получается уравнение для определения υ(x, t):
Если можно пренебречь утечкой через изоляцию (А = 0) и сопротивлением (R = 0), то уравнения (105) и (106) переходят в волновые уравнения:
где обозначено: a 2 = 1/CL. Исходя из физических условий, формулируются граничные и начальные условия задачи.
Решение уравнения колебаний струны методом разделения переменных (методом Фурье).
Метод разделения переменных (или метод Фурье) является типичным для решения многих задач математической физики. Пусть требуется найти решение уравнения
удовлетворяющее краевым условиям:
Будем искать (не равное тождественно нулю) частное решения уравнения (107), удовлетворяющее граничным условиям (108) и (109), в виде произведения двух функций X(x) и T(t), из которых первая зависит только от х, вторая только от t:
u (x, t) = X (x) T (t). (112)
Подставляя в уравнение (107), получаем:
X (x) T′′(t) = a 2 X′′(x) T(t).
Разделив члены равенства на a 2 XT
В левой части этого равенства стоит функция, которая не зависит от х, слева – функция, не зависящая от t. Равенство (113) возможно только в том случае, когда левая и правая части не зависят ни от х, ни от t, т. е. равны постоянному числу. Обозначим его через – λ, где λ > 0 ( позднее будет рассмотрен случай λ 2 λT = 0. (115)
Общие решения этих уравнений будут:
где A, B, C, D – произвольные постоянные.
Подставляя выражения X(x) и T(t) в равенство (112), получим:
Подберем теперь постоянные А и В так, чтобы удовлетворялись условия (108) и (109). Так как T (t) тождественно неравна нулю (в противном случае u (x, t) ≡ 0, что противоречит поставленному условию),то функция X (x) должна удовлетворять условиям (108)
и (109), т. е. должно быть Х (0) =0, Х (ℓ) = 0. Подставляя значения х=0 и х = ℓ в равенство (116), на основании (108) и (109) получаем:
Из первого уравнения находим А = 0. Из второго следует:
В ≠ 0, так как в противном случае было бы Х ≡ 0 и u ≡ 0, что противоречит условию. Следовательно, должно быть
(мы не берем значение n = 0, так как в этом случае было бы Х ≡ 0 и u ≡ 0). Итак, мы получили:
Найденные значения λ называются собственными значениями для данной краевой задачи. Соответствующие им функции Х (х) называются собственными функциями.
Замечание. Если бы мы знали вместо – λ выражение + λ = k 2 , то уравнение (114) приняло бы вид
Общее решение этого уравнения:
Х = Аe kx + Be -kx .
Отличное от нуля решение в такой форме не может удовлетворять граничным условиям (108) и (109).
Зная λ 1/2 , мы пользуясь равенством (117) , можем написать:
Для каждого значения n, следовательно, для каждого λ, выражения (119) и (120) подставляем в равенство (112)и получаем решение уравнения (107), удовлетворяющее граничным условиям (108) и (109). Это решение обозначим un (x, t):
Для каждого значения n мы можем брать свои постоянные C и D и потому пишем Cn и Dn (постоянная В включена в Cn и Dn ). Так как уравнение (107) линейное и однородное, то сумма решений также является решением, и потому функция, представленная рядом
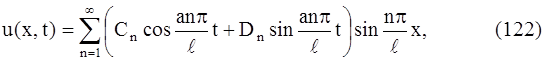
Решение (122) должно еще удовлетворять начальным условиям (110) и (111). Этого мы будем добиваться путем подбора постоянных Cn и Dn . Подставляя в равенство (122)t = 0, получим :
Если функция ƒ(x) такова, что в интервале (0, ℓ) ее можно разложить в ряд Фурье, то условие (123) будет выполняться, если положить
Далее, дифференцируем члены равенства (122) по t и подставляем t = 0. Из условия (111) получается равенство
Определяем коэффициенты Фурье этого ряда:
Итак, мы доказали, что ряд (122), где коэффициенты Cn и Dn определены по формулам (124) и (125), если он допускает двукратное почленное дифференцирование, представляет функцию u (x, t), которая является решением уравнения (107) и удовлетворяет граничным и начальным условиям (108) – (111).
Замечание. Решая рассмотренную задачу для волнового уравнения другим методом, можно доказать, что ряд (122) представляет собой решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция ƒ(x) должна быть дважды дифференцируемой, а функция φ(x) – один раз дифференцируемой.
Уравнение распространения тепла в стержне. Формулировка краевой задачи.
Рассмотрим однородный стержень длины ℓ. Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.
Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = , а другой – с точкой х = ℓ.
Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой
где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.
Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х1 и х2 (х2 – х1 = ∆х). Количество тепла, прошедшего через сечение с абсциссой х1 за время ∆t, будет равно
то же самое с абсциссой х2 :
Приток ∆Q1 — ∆Q2 в элемент стержня за время ∆t будет равняться:
Этот приток тепла за время ∆t затратился на повышение температуры элемента стержня на величину ∆u:
где с – теплоемкость вещества стержня, ρ – плотность вещества стержня (ρ∆xS – масса элемента стержня).
Приравнивая выражения (129) и (130) одного и того же количества тепла ∆Q1 — ∆Q2 , получим:
Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.
Чтобы решение уравнения (131) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (131) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для 0 ≤ t ≤ T, следующие:
Физическое условие (132) (начальное условие) соответствует тому, что при t = 0 в разных сечениях стержня задана температура, равная φ(x). Условия (133) и (134) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х = ℓ поддерживается температура, равная ψ1 (t) и ψ2 (t) соответственно.
Доказывается, что уравнение (131) имеет единственное решение в области 0 ≤ х ≤ ℓ, 0 ≤ t ≤ T , удовлетворяющее условиям (132) – (134).
Распространение тепла в пространстве.
Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u(x, y, z, t) – температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку ∆s, т. е. количество тепла, протекающего за единицу времени, определяется формулой (аналогично формуле (126))
где k – коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n – единичный вектор, направленный по нормали к площадке ∆s в направлении движения тепла. Таким образом, можем записать:
где cos α, cos β, cos γ – направляющие косинусы вектора n, или
Подставляя выражение 
∆Q = -k n grad u ∆s.
Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:
∆Q∆t = -k n grad u ∆t ∆s.
Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:
где n – единичный вектор, направленный по внешней нормали к поверхности S. Очевидно, что формула (136) дает количество тепла, поступающего в объем V(или уходящего из объема V) за время ∆t. Количество тепла, поступившего в объем V, идет на повышение температуры вещества этого объема.
Рассмотрим элементарный объем ∆υ. Пусть за время ∆t его температура поднялась на ∆u. Очевидно, что количество тепла, затраченное на это повышение температуры элемента ∆υ, будет равно
где с – теплоемкость вещества, ρ – плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время ∆t, будет
Но это есть тепло, поступающее в объем V за время ∆t; оно определено формулой (136) . Таким образом, имеет место равенство
Сокращая на ∆t, получаем:
Поверхностный интеграл, стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F – дивергенция векторного поля, σ – замкнутая поверхность)
полагая F = k grad u:
Заменяя двойной интеграл, стоящий в левой части равенства (137), тройным интегралом, получим:
Применив теорему о среднем к тройному интегралу, стоящего слева, получим :
где P(x, y, z) – некоторая точка объема V.
Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (138) непрерывна, то равенство (139) будет выполняться в каждой точке пространства. Итак,
Подставляя в уравнение (140), получаем:
Если k – постоянное, то
и уравнение (140) в этом случае дает:
или, положив
Коротко уравнение (142) записывается так:
где 
Пусть имеем тело Ω, поверхность которого σ. В этом теле рассматривается процесс распространения тепла. В начальный момент температура тела задана. Это соответствует тому, что известно значение решения при t = 0 – начальное условие:
u(x, y, z, 0) = φ (x, y, z). (143)
Кроме того, должна быть известна температура в любой точке М поверхности σ тела в любой момент времени t – граничное условие:
u (М, t) = ψ (М, t). (144)
(Возможны и другие граничные условия.)
Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем уравнение:
— уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные условия, аналогично (143) и (144), формулируются так:
где φ и ψ – заданные функции, М – точка границы С.
Если же функция u не зависит ни от z, ни от y, то получаем уравнение
— уравнение распространения тепла в стержне.
http://www.bestreferat.ru/referat-46743.html
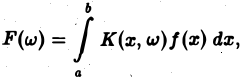

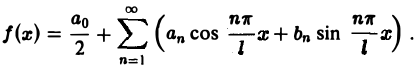
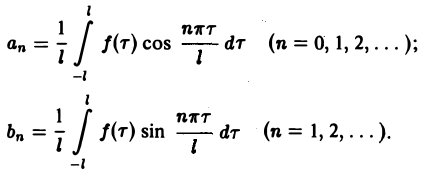
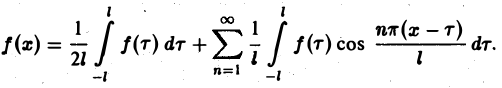
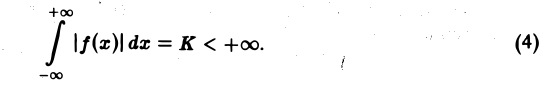
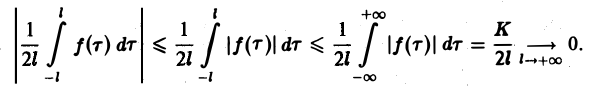
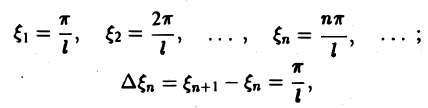
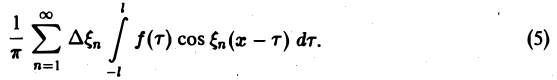
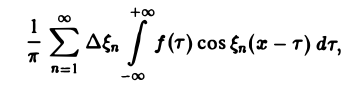
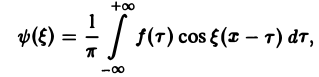
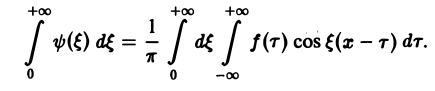
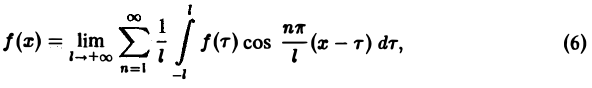
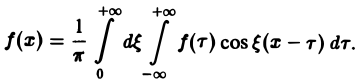
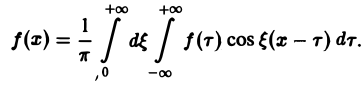
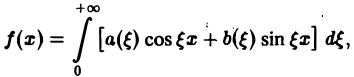
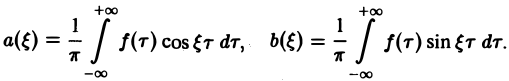
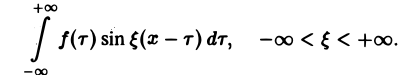
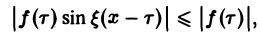
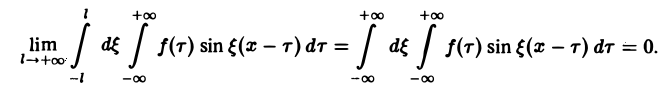
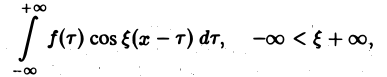
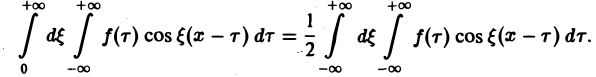
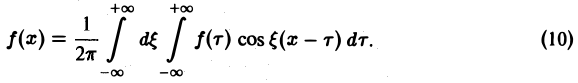
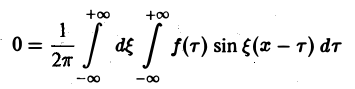
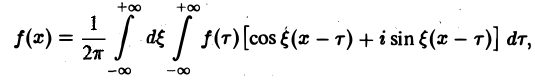
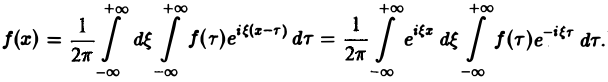
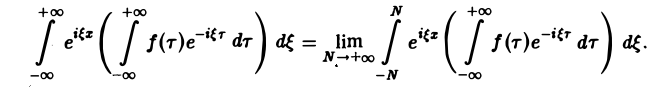
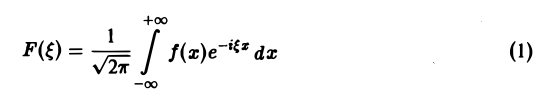
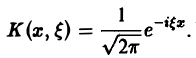
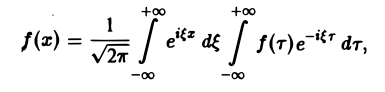
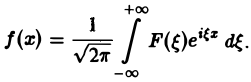
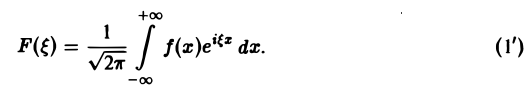
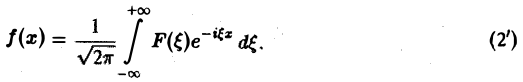
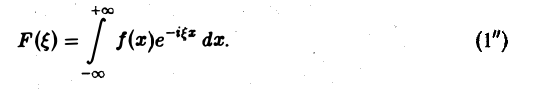
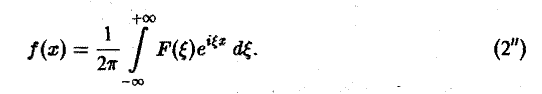
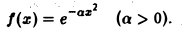
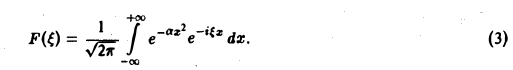
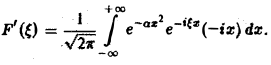
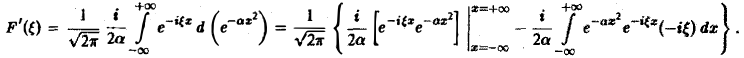
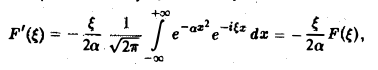

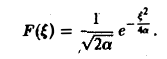
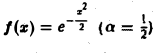
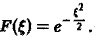
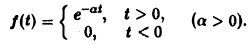
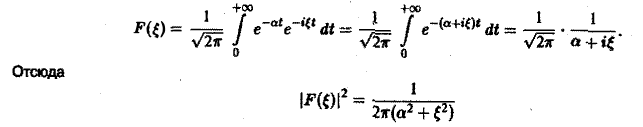
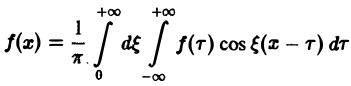
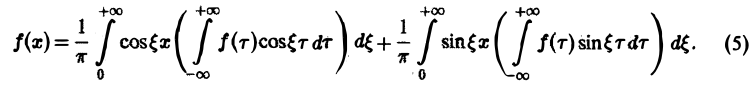
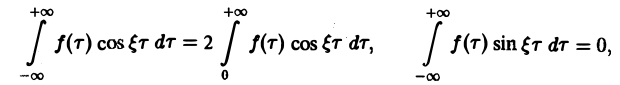
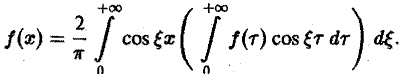
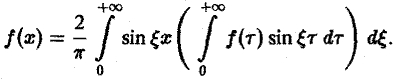
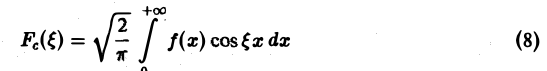
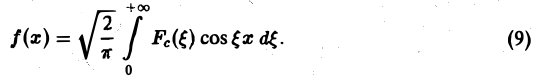
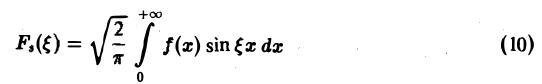
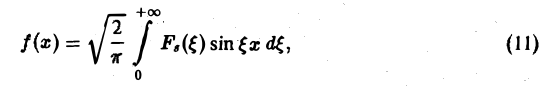
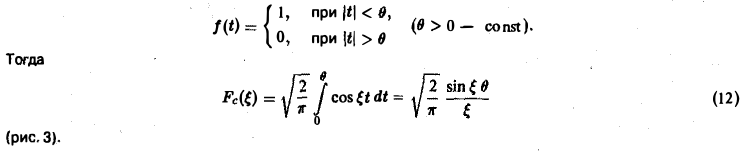
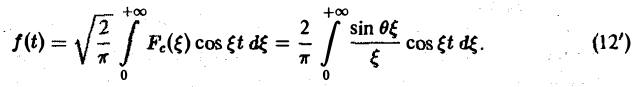
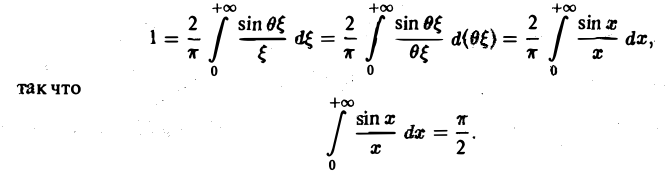
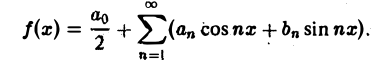
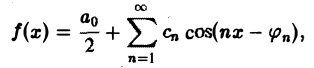
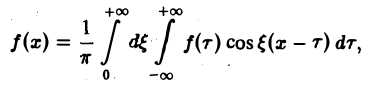
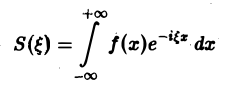
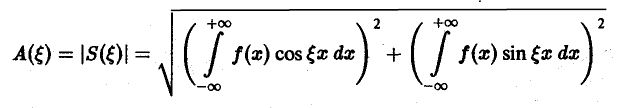
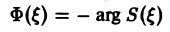
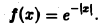
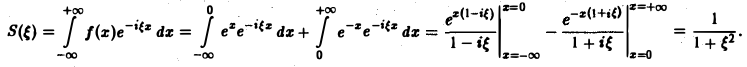
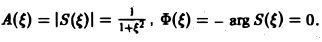
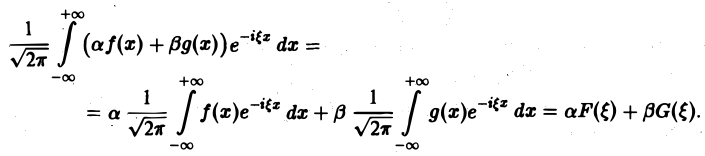
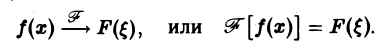
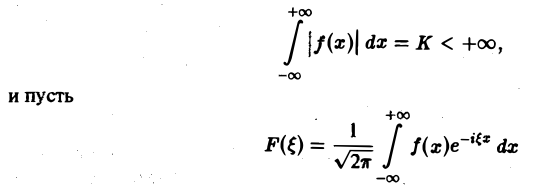
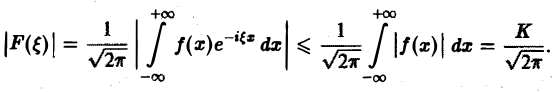
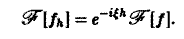
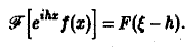
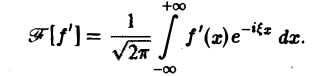
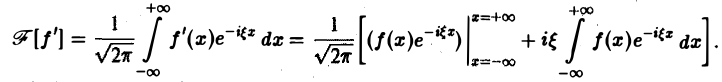
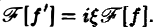
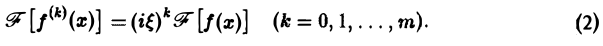
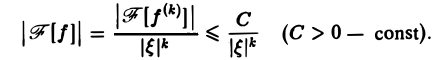
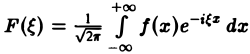
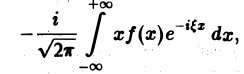
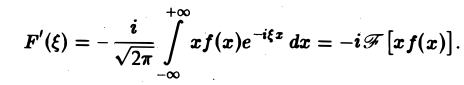
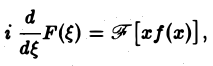
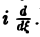
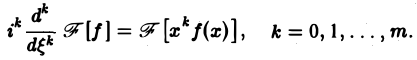
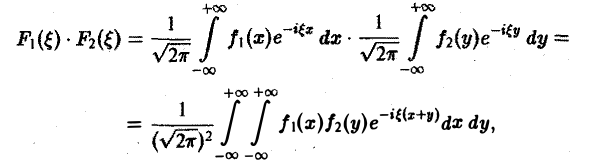
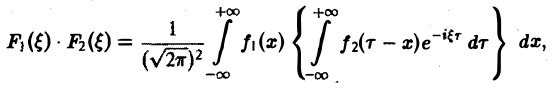
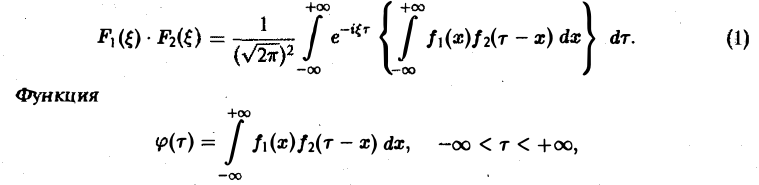
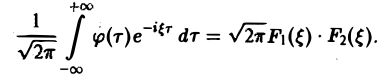
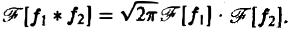
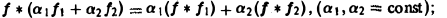
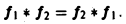
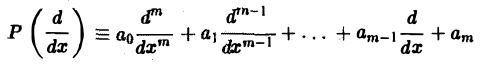
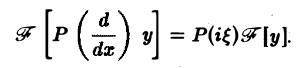


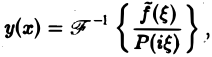
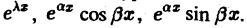
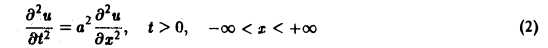
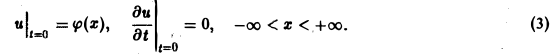
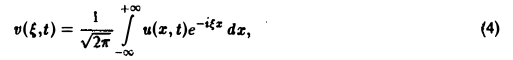
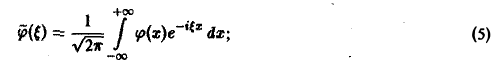
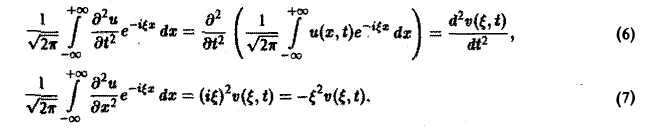


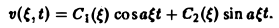
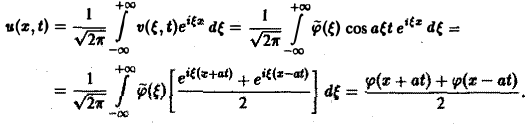
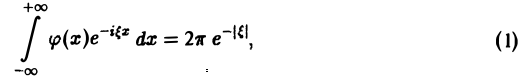
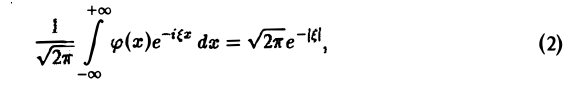
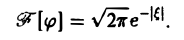
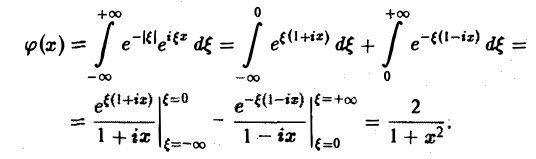

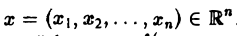
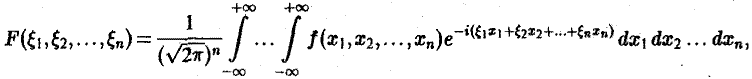
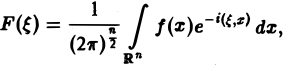
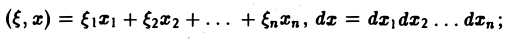
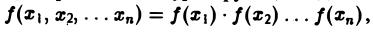
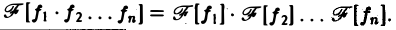


 ( 1 )
( 1 ) (n=1,2. ), он окажется сходящимся и во всех точках вида
(n=1,2. ), он окажется сходящимся и во всех точках вида  (m- любое целое число), и тем самым его сумма S(x) будет (в области сходимости ряда) периодической функцией: если Sn (x) – n-я частичная сумма этого ряда, то имеем
(m- любое целое число), и тем самым его сумма S(x) будет (в области сходимости ряда) периодической функцией: если Sn (x) – n-я частичная сумма этого ряда, то имеем


 , т. е. S(x0 +T)=S(x0 ). Поэтому, говоря о разложении некоторой функции ƒ(x) в ряд вида (1), будем предполагать ƒ(x) периодической функцией.
, т. е. S(x0 +T)=S(x0 ). Поэтому, говоря о разложении некоторой функции ƒ(x) в ряд вида (1), будем предполагать ƒ(x) периодической функцией. (3)
(3) .
. ,
, ,
, .
. , откуда
, откуда . (4)
. (4) (6)
(6)

 (8)
(8) (9)
(9) и учитывая, что ƒ(x) – периодическая функция, получим
и учитывая, что ƒ(x) – периодическая функция, получим