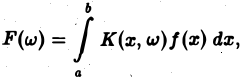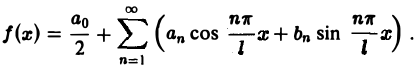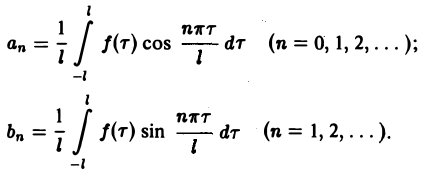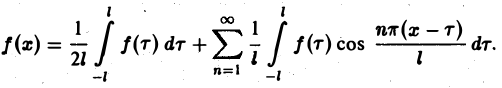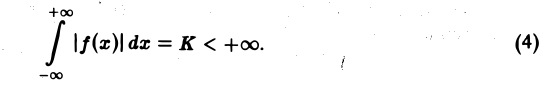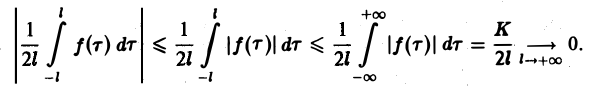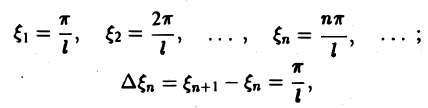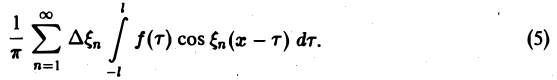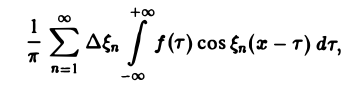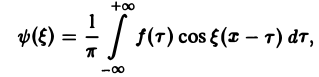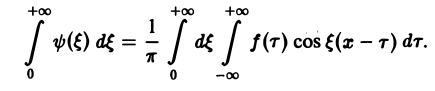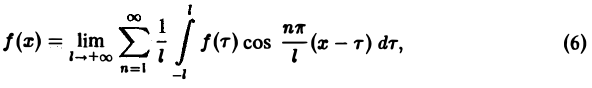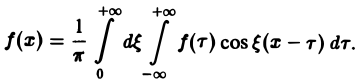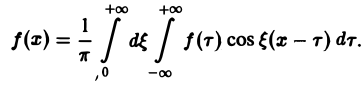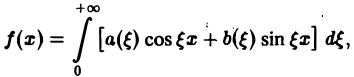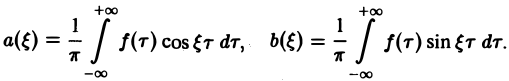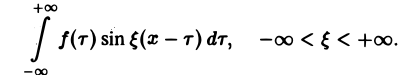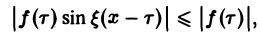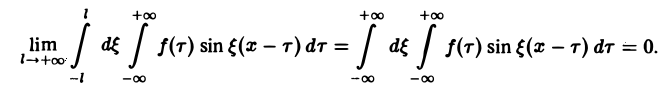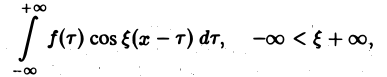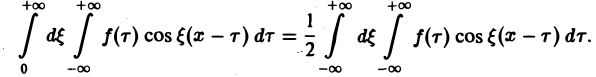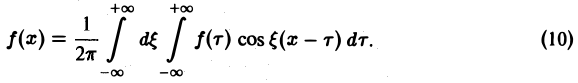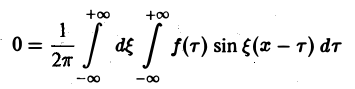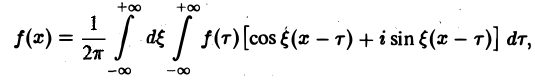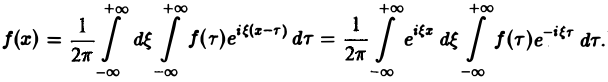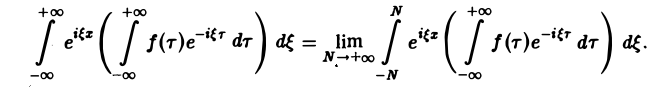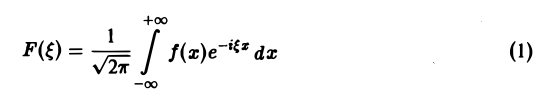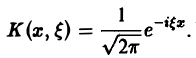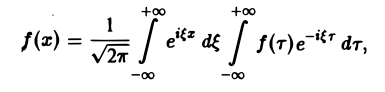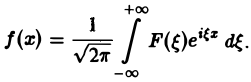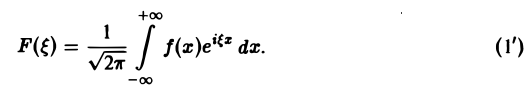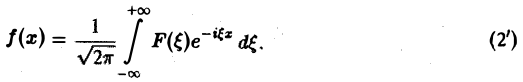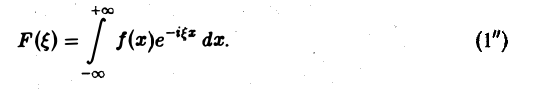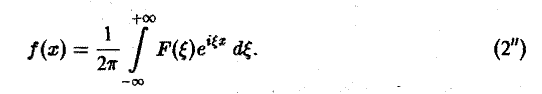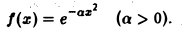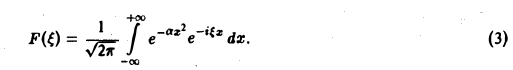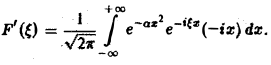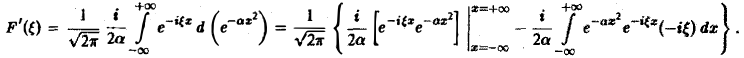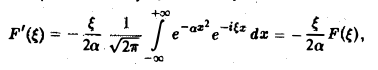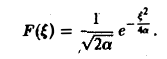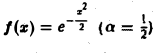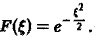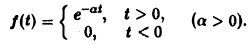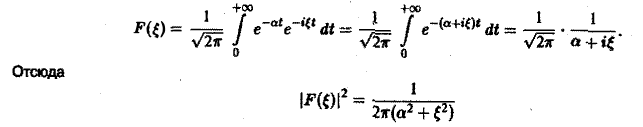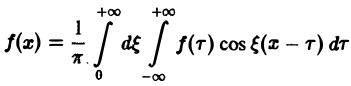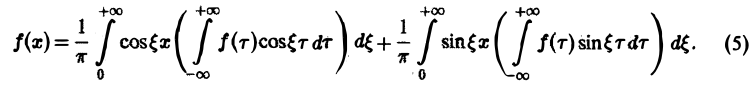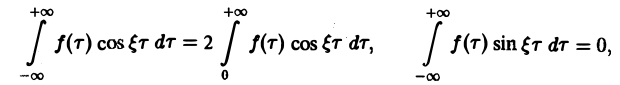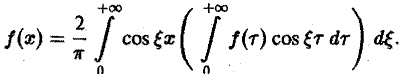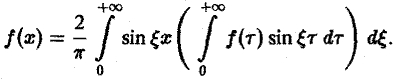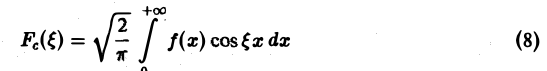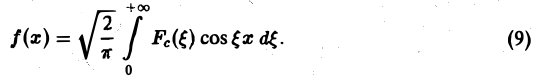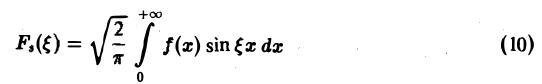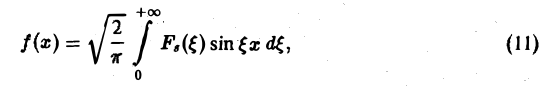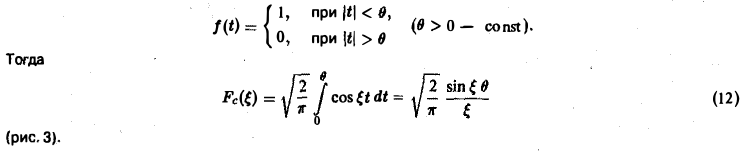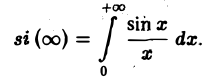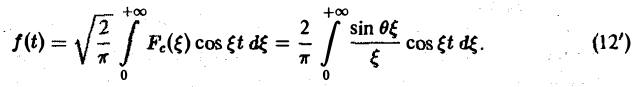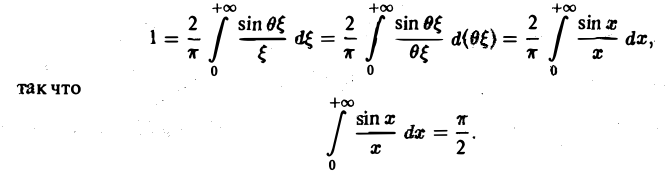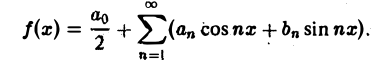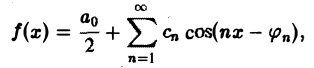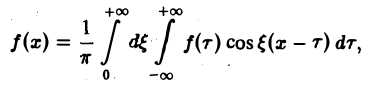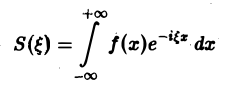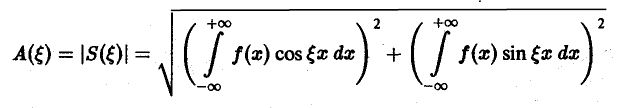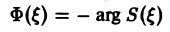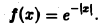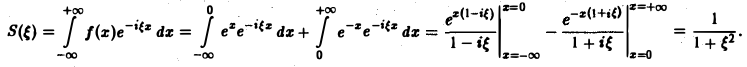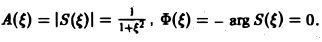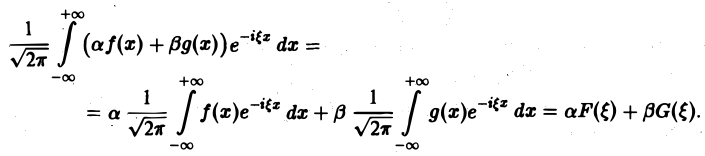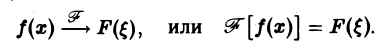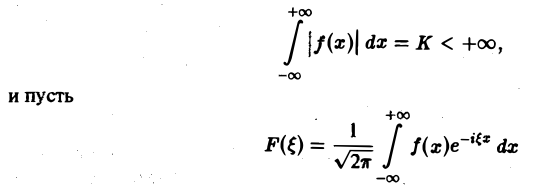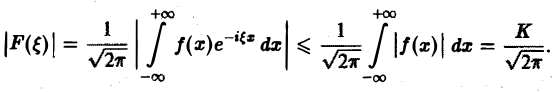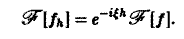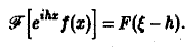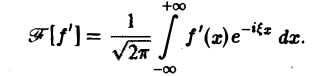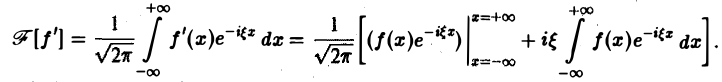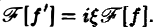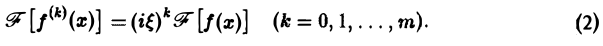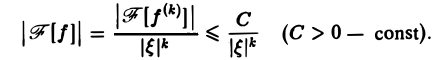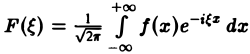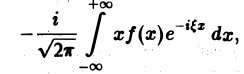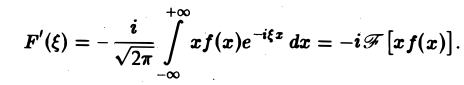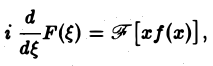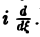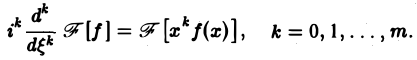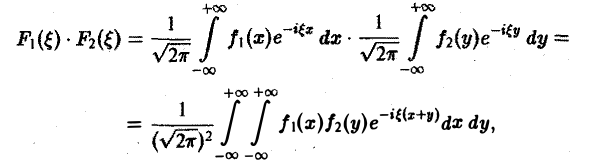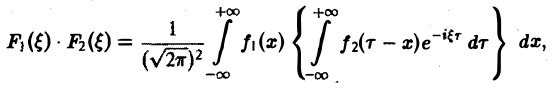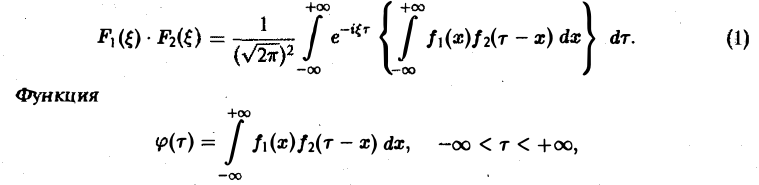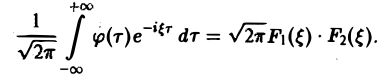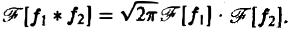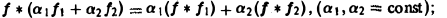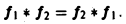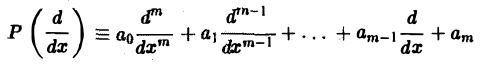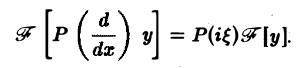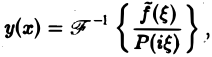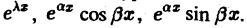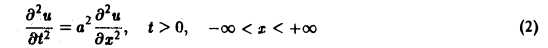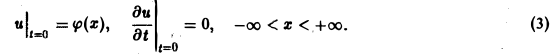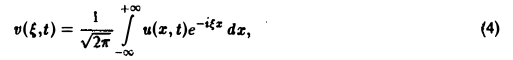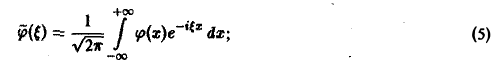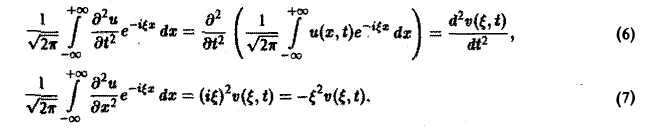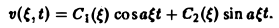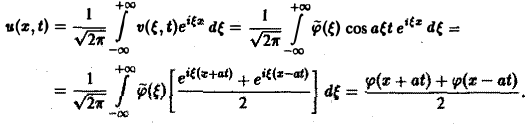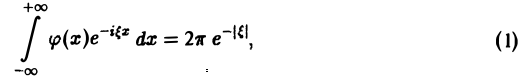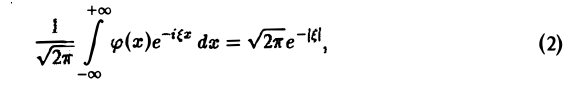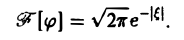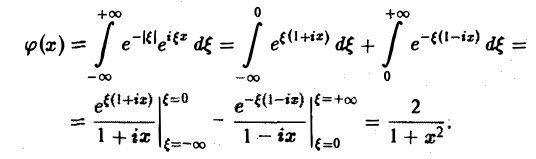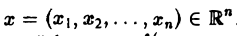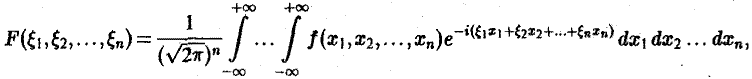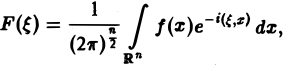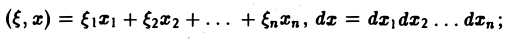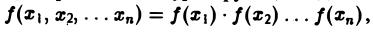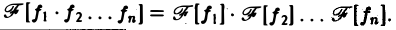Коган Е.А., Лопаницын Е.А. РЯДЫ ФУРЬЕ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- Лев Пантелеев 5 лет назад Просмотров:
1 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ МАШИНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ МАМИ Коган Е.А., Лопаницын Е.А. РЯДЫ ФУРЬЕ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ Учебное пособие по дисциплине «Математика» для студентов всех специальностей и направлений подготовки дипломированных специалистов и бакалавров очного отделения Одобрено методической комиссией по математическим и естественно-научным дисциплинам Москва
2 Разработано в соответствии с Федеральным государственным образовательным стандартом ВПО г. для студентов всех специальностей и направлений подготовки дипломированных специалистов и бакалавров очного отделения на основе рабочей программы дисциплины «Математика». Рецензенты: проф., д.т.н. Ю.Г.Балакирев, кафедра «Прикладная и вычислительная математика» им. Э.И.Григолюка университета машиностроения; проф., д.ф.- м.н. В.И.Мышенков, кафедра «Математическое моделирование» Московского государственного университета леса. Работа подготовлена на кафедре «Прикладная и вычислительная математика» им. Э.И.Григолюка Ряды Фурье и дифференциальные уравнения математической физики. Учебное пособие по дисциплине «Математика» для студентов всех специальностей и направлений подготовки дипломированных специалистов и бакалавров очного отделения. ФГБОУ ВПО «Московский государственный машиностроительный университет МАМИ».. 37 с. Пособие предназначено для изучения разделов дисциплины «Математика», посвящённых рядам Фурье и уравнениям математической физики. Оно содержит теоретические сведения в объёме лекционного курса и подробно разобранные примеры решения типовых задач. Пособие может быть использовано студентами в качестве руководства для самостоятельной работы и преподавателями для проведения практических занятий. Библ., илл.8. Коган Е.А., Лопаницын Е.А. Университет машиностроения,
3 3 СОДЕРЖАНИЕ Часть. Ряды Фурье.. 5 Введение. 5. Постановка основной задачи гармонического анализа и её решение.. 7. Различные формы разложения функций в ряд Фурье Ряды Фурье для чётных и нечётных функций с периодом T Ряд Фурье для функций с произвольным периодом T Разложение в ряд Фурье непериодических функций 7.. Разложение в ряд Фурье функции f, определённой на отрезке [, ] Комплексная форма ряда Фурье. 6. Обобщённый ряд Фурье. Ортонормированные системы функций Применение рядов Фурье к интегрированию дифференциальных уравнений. 7 Часть. Дифференциальные уравнения математической физики Классификация уравнений и постановка задач математической физики Уравнения гиперболического типа Задача о собственных колебаниях струны Вывод волнового уравнения Постановка начально-краевой задачи для волнового уравнения Решение однородного волнового уравнения методом разделения переменных методом Фурье. Продольные колебания стержня Решение неоднородного волнового уравнения методом разложения по собственным функциям Задача о вынужденных колебаниях струны при отсутствии начальных возмущений Решение задачи о вынужденных колебаниях струны с учётом начальных возмущений Редукция общей неоднородной начально-краевой задачи для волнового уравнения.. 58
4 . Решение волнового уравнения в круговой области Уравнение и функции Бесселя Осесимметричные колебания круговой мембраны Уравнения параболического типа Вывод уравнения теплопроводности стержня Постановка начально-краевых задач для уравнения теплопроводности стержня Решение однородного уравнения теплопроводности методом разделения переменных Решение уравнения теплопроводности для случая стационарной неоднородности Решение начально-краевой задачи для неоднородного уравнения теплопроводности со смешанными однородными граничными условиями Решение уравнения теплопроводности в полярных координатах Уравнения эллиптического типа. 8.. Постановка краевых задач для уравнения Лапласа Фундаментальные решения уравнения Лапласа 8.3. Решение задачи Дирихле для уравнения Лапласа в прямоугольной области Решение уравнения Пуассона Решение краевой задачи для уравнения Пуассона в виде двойного тригонометрического ряда Фурье Уравнение Гельмгольца Решение уравнения Гельмгольца в прямоугольной области Решение уравнения Гельмгольца в круговой области Бигармоническое уравнение. Решение Навье Варианты расчётно-графической работы 6 Литература.. 36
5 5 Часть. РЯДЫ ФУРЬЕ Введение Тригонометрические ряды Фурье представляют собой эффективный математический аппарат, который широко применяется в математике для решения обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, в задачах интерполяции, аппроксимации, обработки сигналов и экспериментальных данных и др. Особенно широко применяются ряды Фурье при изучении колебательных и периодических процессов и явлений. Поэтому рассмотрим, прежде всего, определение и свойства периодических функций, которые нам понадобятся в дальнейшем. Как известно, функция f, определённая на всей числовой оси, называется периодической, если существует постоянное число T> такое, что для любого, взятого из области её определения, справедливо равенство f T f. Геометрически периодическая функция характеризуется тем, что ординаты любых двух точек, абсциссы которых отличаются на величину, кратную периоду, равны между собой. Можно указать следующие основные свойства периодических функций.. Если Т период функции f, то и T тоже её период, где любое целое число. Это следует сразу из последовательного рассмотрения равенств f f T f T f T. Следовательно, если функция f периодическая, то она имеет множество периодов. Поэтому обычно под периодом функции подразумевают наименьший из всех положительных периодов.. Если функция f имеет период Т, то функция ϕ f имеет период T/. Действительно, ϕ T f [ T ] f T f ϕ. 3. Если функция f имеет период Т, то интеграл от этой функции, Ф у р ь е Жан Батист Жозеф марта мая 83 французский математик.
6 6 взятый в пределах, отличающихся на период, не зависит от положения интервала интегрирования на числовой оси, то есть при любом T f d T f d Действительно, как известно, определённый интеграл численно равен площади под кривой f на интервале интегрирования. Но, как видно из рис., заштрихованные площади для обоих интегралов от периодической функции f равны при любом. Рис..
7 7. Постановка основной задачи гармониче ского анализа и её решение Наиболее распространённым и важным для приложений примером периодических функций являются так называемые гармоники. Это функции вида y Asi ω t ϕ, описывающие незатухающие гармонические колебания с амплитудой A, частотой ω и начальной фазой ϕ. Они могут быть также записаны в виде y siωt bcosωt. Очевидно, период этих функций по свойству равен /ω. Легко убедиться в том, что при сложении гармоник разной частоты график результирующей функции будет заметно отличаться по виду от графика каждой из составляющих. Например, суммой синусоидальных функций разных аргументов f si t,5si t,3si 3t,si t будет периодическая функция с периодом, равным периоду основного члена этой суммы si t, график которой, как видно, существенно отличается от синусоиды см. рис.. Рис..
8 8 На практике большое значение имеет обратная задача: можно ли и при каких условиях разложить произвольную периодическую функцию f с периодом T на сумму простых гармоник разной частоты, то есть представить её в виде суммы гармонических колебаний. Эта задача и составляет предмет гармонического анализа или теории рядов Фурье. Отметим, в дополнение к сказанному во введении, что метод разложения произвольной периодической функции на сумму простейших периодических функций оказался исключительно эффективным для решения задач, возникающих в самых разных областях естествознания и техники: в механике абсолютно твердого и деформируемого тела, в гидро- и аэромеханике, в теории колебаний, в электротехнике и радиотехнике, в акустике, при расчёте различных конструкций и инженерных сооружений и т.п. Многочисленные примеры применения гармонического анализа для решения различных прикладных задач широко освещены в учебной и научной литературе. Для решения поставленной основной задачи гармонического анализа предварительно введём понятие основной тригонометрической системы функций. Это система функций вида:, cos, si, cos, si. cos, si. Все функции, её образующие, имеют общий период хотя в соответствии со свойством периодических функций cos и si имеют и меньший период /. Единица может рассматриваться, как постоянная величина, имеющая любой период, в частности,. Рассмотрим интегралы от произведения функций, образующих основную тригонометрическую систему. Все интегралы будем вычислять на отрезке [, ] длиной, равной периоду. Будем различать 3 случая. Для любых целых интегралы от произведения единицы на произвольные cos и si si cos d, cos cos cos si d. Воспользуемся далее известными формулами преобразования произведения тригонометрических функций в сумму:
9 9 cosα cos β [cos α β cos α β ], siα si β [cos α β cos α β ], siα cos β [si α β si α β ]. Для любых целых и m m cos cosmd [cos m cos m ] d si m m si m m si si md [cos cos ] m m d, si cosmd 3 При m [si m si m ] d cos m m si cosmd si d, cos m m,. cos si cos d d, cos si d d. Как видно, все интегралы от произведения функций, стоящих на разных местах в основной тригонометрической системе, равны нулю. Говорят, что функции ϕ и ϕ m,m. ортогональны на отрезке [, b], если при m
10 При этом предполагается, что b b ϕ ϕm d. ϕ d. Поэтому можно сказать, что функции, образующие основную тригонометрическую систему, попарно ортогональны на отрезке [, ]. А по свойству 3 периодических функций можно заключить, что функции, образующие основную тригонометрическую систему, попарно ортогональны на любом отрезке [, ]. Вернёмся теперь к решению основной задачи гармонического анализа. Предположим, что произвольную периодическую функцию с периодом T можно представить в виде равномерно сходящегося тригонометрического ряда f cos b si cos b si cos b si. то есть представить в виде суммы гармоник разной частоты. Напомним, что бесконечный функциональный ряд f f f f. f. называется сходящимся для данного значения, если существует конечный предел s im s его частичных сумм s m f m. Величина s называется суммой ряда, и для ряда, сходящегося для всех из отрезка [, b], сумма ряда определена на [, b]. При этом функциональный ряд сходится равномерно на [, b], если для любого заданного ε > существует такой, не зависящий от, номер N, что для всех > N неравенство s s ε выполняется одновременно для всех [, b].
11 Свойство равномерной сходимости означает, что при достаточно больших графики суммы ряда s и соответствующих частичных сумм s отличаются друг от друга менее чем на заданную малую величину ε. Равномерно сходящиеся ряды можно почленно интегрировать и дифференцировать, то есть для них допустима перестановка порядка суммирования и интегрирования [8] b b f d f d, f f. Воспользуемся этим свойством равномерно сходящихся рядов и свойством ортогональности тригонометрических синусов и косинусов для нахождения неизвестных коэффициентов ряда.. Сначала проинтегрируем равенство. почленно на отрезке ортогональности тригонометрических синусов и косинусов [, ]: f d d cos d b si d. В силу ортогональности тригонометрических синусов и косинусов все интегралы в правой части под знаком суммы равны нулю. Следовательно, получаем f d.. Умножим теперь почленно равенство. на cosm и проинтегрируем на промежутке [, ]. Тогда f cos md cos md cos cos md b si cosmd. В правой части, из-за ортогональности тригонометрических функций, будут равны нулю первое слагаемое и все интегралы под знаком суммы, кроме интеграла от произведения косинусов при m. Поэтому из всей суммы остаётся одно слагаемое: f cosd cos d.
12 Следовательно, f cos d..3 Аналогично, умножая равенство. почленно на sim и интегрируя в пределах от до, получим b f si d.. Такой подход к определению коэффициентов был применён Л.Эйлером во второй половине XVIII века, а позднее и независимо от него Ж.Фурье. Равномерно сходящийся тригонометрический ряд., коэффициенты которого определяются по формулам. называется рядом Фурье для функции f. Условия, при которых справедливо разложение., устанавливаются так называемыми условиями Дирихле 3. Говорят, что функция f на отрезке [, b] удовлетворяет условиям Дирихле, если она на этом интервале кусочно-монотонна и ограничена см. рис.3. Рис.3. Функция f кусочно-монотонна на отрезке [, b], если его можно разбить конечным числом точек. на интервалы. b так, что на каждом из них функция монотонна, то Э й л е р Леонард 5 марта 77 8 сентября 783 швейцарский механик, физик и математик, с 77 г. по 7г. и с 766 г. до конца жизни жил и работал в России. 3 Д и р и х л е Петер Густав Лежëн 3 февраля 85 5 мая 859 французский математик.
13 3 есть либо невозрастающая, либо неубывающая. Функция f кусочно-монотонная и ограниченная на [, b], может иметь на этом отрезке только точки разрыва -го рода, то есть такие точки разрыва, для которых существуют конечные предельные значения функции при приближении её к точке разрыва c слева и справа рис.3: im f f c, im f f c. c c Можно показать, что справедлива следующая теорема о разложимости функции в ряд Фурье: если периодическая функция f с периодом удовлетворяет условиям Дирихле, то она может быть представлена в виде равномерно сходящегося тригонометрического ряда Фурье f cos b si, причём сумма членов полученного ряда S равна значению функции f в тех внутренних точках интервала,, в которых функция f непрерывна. В точках разрыва функции f сумма ряда Фурье равна среднему арифметическому предельных значений функции слева и справа от точки разрыва c, то есть f c f c S c,.5 а на концах интервала сумма равна f f S ±. Замечание. Условиям теоремы разложимости удовлетворяет весьма широкий класс функций. Так, для разложения функции в ряд Тейлора f f f f f. требуется, чтобы функция была не только непрерывной, но и бесчисленное число раз дифференцируемой так как коэффициенты ряда Тейлора выражаются через начальные значения функции и её производных, а в ряд Фурье можно разложить функцию не только непрерывную, но и имеющую точки разрыва -го рода. Т е й л о р Брук 8 августа декабря 73 английский математик.
14 Кроме того, в степенные ряды нельзя разлагать функции, выражающиеся на разных отрезках различными формулами. Тригонометрические ряды Фурье позволяют осуществлять разложение функций, заданных разными выражениями на разных отрезках. Поэтому ряды Фурье применяются очень широко.
15 5. Р азличные формы разложения функций в ряд Фурье.. Ряды Фурье для чётных и нечётных функций с периодом T Если функция f является чётной, то есть f f, то её график симметричен относительно оси ординат и f d f d. Тогда формулы.. упрощаются. Действительно, подынтегральная функция fsi является нечётной, и b как интеграл от нечётной функции в симметричных пределах, а коэффициент будет равен f cosd f cosd. так как подынтегральная функция fcos является чётной. Таким образом, ряд Фурье для чётной функции, удовлетворяющей условиям Дирихле, не содержит синусов и имеет вид причём f cos,. f cosd. Если функция f является нечётной, то есть f f, то её график симметричен относительно начала координат. Тогда, и так как функция fcos является нечётной, то как интеграл от нечётной функции в симметричных пределах. Функция fsi будет чëтной, и коэффициент b будет равен b f si d f si d. Поэтому ряд Фурье для нечётной функции, удовлетворяющей условиям Дирихле, содержит только синусы и имеет вид f b si,.3
16 6 причём b f si d,,3, Ряд Фурье для функций с произвольным периодом T Если f периодическая функция с периодом T где > полупериод функции есть произвольное число, удовлетворяющая условиям Дирихле, то выполняя замену переменной по формуле t/, получим функцию f t ϕ переменной t с периодом. Её можно обычным образом разложить в ряд Фурье на отрезке [, ]: f f t ϕ cost b si, где ϕ costdt f t costdt. b ϕ si tdt f t si tdt,,3. Возвращаясь далее к старой переменной, то есть полагая t / и учитывая, что dt d/, получим в точках дифференцируемости f cos b si,.5 где f d, f cos d,.6 b f si d. Ряд.5, коэффициенты которого определяются по формулам.6, также называется рядом Фурье для функции f с периодом T. В точках разрыва функции f сумма ряда Фурье.5 будет определяться по формуле.5. Аналогично.. и соответственно.3. получим ряд Фу-
17 7 рье для чётной функции с периодом T : f cos,.7 f cos d. 8 и ряд Фурье для нечётной функции с периодом T : f b si,.9 b f si d,,3, Разложение в ряд Фурье непериодических функций Пусть f непериодическая, кусочно-монотонная и ограниченная функция, заданная на конечном отрезке [, ]. Присоединим к графику заданной функции все его горизонтальные смещения на расстояния, кратные на рис. они показаны пунктиром. Рис.. Тогда получим так называемое периодическое продолжение заданной функции на всю числовую ось. Получившаяся периодическая вспомогательная функция f *, определённая на всей числовой оси, в соответствии с теоремой о разложимости может быть представлена в виде ряда Фурье.5,.6. Но для всех,, кроме точек разрыва ±, значения * вспомогательной функции совпадают с заданной: f f. Следовательно, сумма членов ряда Фурье для вспомогательной функции во всех точках,, кроме точек разрыва, даст значения заданной функции. Поэтому разложение непериодической функции в
18 8 ряд Фурье в действительности осуществляется без привлечения вспомогательной функции непосредственно по формулам.5 и.6. Пример. Разложить в ряд Фурье функцию f, заданную на отрезке [-,]. при 19 9 cos si. Коэффициенты b определяются аналогично: b si d si d si d cos cos. Таким образом, ряд Фурье для заданной функции примет вид cos f si cos cos cos si или f cos si cos si Во всех точках непрерывности функции f сумма ряда S совпадает с её значениями, а в точках разрыва она будет равна: S S S,5. Разложение в ряд Фурье функции f, определённой на отрезке [,] Функцию f, определённую на отрезке [, ] и являющуюся на этом отрезке кусочно-монотонной и ограниченной, можно разложить в ряд Фурье многими способами. Для этого сначала надо представить продолжение функции на интервал [, ]. Это можно сделать многими способами, но основными являются следующие два. Если продолжение f на интервал [, ] чётное симметричное относительно оси ординат, то ряд Фурье можно записать по формулам.7 и.8, то есть по косинусам. Если продолжить функцию f на [, ] нечётным образом, то разложение в ряд Фурье будет представлено формулами.9 и., то есть по синусам. При этом оба ряда будут иметь в интервале, одну и ту же сумму. Пример. Разложить в ряд Фурье функцию f, заданную на
20 промежутке [, ]. Первое решение разложение в ряд по косинусам. Строим чётное продолжение функции в соседний полуинтервал [, ]. График функции f вместе с её чётным продолжением на [, ] и периодическим продолжением с T на всю ось показан на рис.6. Рис.6. Так как, то ряд Фурье для данной функции при чётном разложении будет иметь вид f cos,.3 при этом f d d, f cos d cosd. В результате получим при cos. cos cos3 cos На всей оси ряд сходится к функции, изображённой на рис.6. Второе решение разложение в ряд по синусам. Строим нечётное продолжение функции в соседний полуинтервал [,]. График функции f вместе с её нечётным продолжением на [,] и последующим периодическим продолжением на всю числовую ось показан на рис.7. При нечётном разложении f b si,.5
21 где b si d. Рис.7. Поэтому ряд Фурье по синусам для данной функции при 22 . является её рядом Фурье. Воспользуемся формулами Эйлера, связывающими показательную функцию комплексного аргумента z с тригонометрическими синусом и косинусом e iz cos z isi z, e iz cos z isi z и следствием из них iz iz iz iz e e e e cos z, si z, i и преобразуем общий член тригонометрического ряда Фурье к виду i i i i e e e e cos b si b i i i i i e e e e ib i ib i ib e e i i ce ce, где ib ib c, c,,3. Положим далее c, тогда частичные суммы ряда Фурье можно представить в виде N N N i i i cos b si c c e c e c e. N Учитывая формулы.3,. и формулу Эйлера, получим выражение для комплексных коэффициентов Фурье: ib c f cosd i f si d i cos si, > f i d f e d. Эта формула справедлива и для, так как тогда c f d, и при 23 c ib c f cos i si d 3 f e где c означает комплексное число, сопряжённое c. В пределе при N найдём N N i i f im ] cos b si im ce ce. N N N Полученный ряд f i c e, коэффициенты которого определяются по формуле i c f e d, ±, ±. i d, и называется рядом Фурье для функции с периодом в комплексной форме. Для функции f с произвольным периодом T ряд Фурье в комплексной форме имеет вид где f i c e i c f e d, ±, ±, Обобщённый ряд Фурье. Ортонормированные системы функций Пусть функция f, определённая на отрезке [, b], может быть разложена в ряд по системе ортогональных на [, b] функций ϕ : f ϕ ϕ ϕ ϕ. ϕ. 7 где коэффициенты i i. являются постоянными числами. Для определения коэффициентов разложения i умножим равенство.7 на ϕ m и проинтегрируем почленно на отрезке [, b]. Получим равенство
24 b f ϕ m d ϕ ϕm d ϕ ϕm d. b b b ϕ ϕm d. В силу ортогональности функций ϕ все интегралы в правой части равенства будут равны нулю, кроме одного, когда m. Отсюда следует, что b b f ϕ d..8 ϕ d Ряд.7, коэффициенты которого определяются по формуле.8, называется рядом Фурье по данной ортогональной системе функций или обобщённым рядом Фурье для функции f [8]. Для упрощения формул для коэффициентов применяют так называемое нормирование функций. Система функций ϕ, ϕ,, ϕ, называется нормированной на отрезке [, b], если b ϕ d..9 Справедлива теорема: всякую ортогональную систему функций можно нормировать. Это означает, что можно подобрать брать постоянные числа µ, µ,, µ, так, чтобы система функций µ ϕ, µ ϕ,, µ ϕ, была не только ортогональной, но и нормированной. Действительно, из условия следует, что Число b µ ϕ µ ϕ d b d µ.. b ϕ d
25 5 b ϕ ϕ называется нормой функции ϕ. Если система функций нормирована, то, очевидно, ϕ. Последовательность функций ϕ, ϕ,, ϕ,, определённых на [, b], является ортонормированной на этом отрезке, если все функции нормированы и взаимно ортогональны на [, b]. Для ортонормированной системы функций коэффициенты обобщённого ряда Фурье равны b f ϕ d.. Пример. Разложить функцию y 3 на отрезке 3/ в обобщённый ряд Фурье по системе ортогональных на этом отрезке функций, в качестве которых взять собственные функции задачи на собственные значения ϕ λ ϕ,, λ, ϕ, ϕ 3/, предварительно проверив их на ортогональность. Решение. На первом этапе решаем задачу на собственные значения. Так как общее решение уравнения ϕ λ ϕ будет ϕ C cosλ C si λ, то ϕ C λ si λ Cλ cosλ и из граничных условий следует 3λ C, Cλ cos. При λ общее решение уравнения будет ϕ C C, и из граничных условий получим C C, следовательно, приходим к тривиальному решению. Поэтому для существования нетривиального решения ϕ необходимо принять 3λ cos. Из этого тригонометрического уравнения находим d
26 6 3λ. Поэтому собственные значения параметра λ равны λ, 3 а соответствующие им собственные функции с точностью до множителя С будут ϕ si.. 3 На втором этапе проверяем ортогональность собственных функций на отрезке [, 3/]: 3/ m si si d 3 3 3/ m m cos cos d m 3 m si si 3 3 m m так как si m si m. При этом 3/ 3 3/ 3 si d cos d 3. 3/, Следовательно, собственные функции ϕ si 3 на отрезке [, 3/] ортогональны. На последнем этапе раскладываем заданную функцию в ряд Фурье по системе ортогональных собственных функций.: y 3 si.3 3 и находим
27 7 3 3 si 3 si 3 3/ 3/ d d.. Подставляя. в.3, окончательно получим 3 si 3 3 m.
28 8 3. Применение рядов Фурье к интегрированию дифференциальных уравнений Рассмотрим применение рядов Фурье к интегрированию обыкновенных дифференциальных уравнений на примерах различных краевых задач. Одним из ярких примеров таких задач является задача об изгибе балки постоянного поперечного решения, различным образом закреплённой на концах. Дифференциальное уравнение изгиба балки может быть записано в виде IV EI w q 3. z где w прогиб балки в произвольном поперечном сечении с абсциссой, EI z cost изгибная жёсткость балки E модуль упругости материала, I z момент инерции поперечного сечения. Пусть поперечная нагрузка на разных участках балки задана в виде см. рис.8 а б 8q q q Рис.8. при при при 29 9 левом конце и жёстко защемлённой на правом см. рис.8а. Раскладываем функцию q в ряд Фурье по синусам на отрезке [, ] q b si, 3.3 где b q si d / / 8q si d si d q si d / / q 8 cos cos cos si 3. Подставляем 3.3 в уравнение 3.: IV EI w b si. 3.5 z Уравнение 3.5 допускает непосредственное интегрирование. Интегрируя его первый раз EI получим уравнение 3-го порядка: Аналогично находим EI EI z EI w IV d b si d, w b z cos C w z b si C 3 w z b cos C C Интегрируя последнее уравнение, получим общее решение дифференциального уравнения 3. в виде: EI 3 z w b si C C C3 6 C, C 3. C. 3.6
30 3 Для определения произвольных постоянных С, С, С 3 и С подставляем решение 3.6 в граничные условия 3.. Из первых двух условий при следует C C. 3.7 При из третьего и четвертого граничных условий получим систему двух линейных алгебраических уравнений относительно произвольных постоянных С и С 3 :. cos, b C C C C 3.8 Разрешая систему.37 и учитывая, что cos, находим 3 3 b C, b C. 3.9 Подставляя 3.7, 3.9 в 3.6, получим решение краевой задачи в виде b b b w EI т z si или после подстановки b и элементарных преобразований si 8 cos cos z EI q w si. При / прогиб балки будет si 8 cos cos z EI q w 6 3 si. При вычислении прогиба балки в середине пролета можно ограничиться первыми тремя членами ряда, поскольку, из-за наличия в
31 3 коэффициентах ряда множителя / четвёртое слагаемое даст поправку не более,%. В результате найдём значение прогиба балки в середине пролета: q w /,33. EI z Второй вариант закрепления балки. Пусть балка свободно опёрта на обоих концах рис.8б. Тогда граничные условия запишутся в виде: при w w, при w w 3. Для данного варианта граничных условий искомая функция w может быть разложена в ряд Фурье по синусам на промежутке [, ], равном длине балки: w W si, 3. так как каждый член ряда 3. удовлетворяет всем граничным условиям 3.. Подставляя 3. в уравнение 3., получим EI z W si q 3. Далее раскладываем в ряд Фурье по синусам на отрезке [, ] правую часть уравнения 3., то есть принимаем q b si. При этом коэффициент b для заданной нагрузки см. рис.8 будет определяться по формуле 3.. Подставляя такое представление q в 3., получим равенство EI из которого следует z W si EI zw b b si, 3.3 Из 3.3 с учётом 3. неизвестный коэффициент разложения прогиба W выразится через известный коэффициент разложения нагрузки по формуле
32 W b EI z q 5 EI z 3 cos cos Поэтому решение краевой задачи 3. и 3. примет вид q w 5 EI z 5 cos cos 8 si. 8 si si. Так как ряд сходится очень быстро, то, ограничиваясь его первым членом, при / получим q w /,9. EI z Пример. В виде ряда Фурье найти решение краевой задачи y y q, 3, y, y 3, 9 где q ограниченная, кусочно-непрерывная на отрезке [, 3] функция 3 при 33 3 3 3 si d cos 6 3 d. Подставляя ряд 3. в уравнение, приходим к равенству 33 Y si q Далее раскладываем в обобщённый ряд Фурье по той же ортогональной системе функций правую часть уравнения 3.5 q Q si Коэффициенты ряда 3.6 находим по формуле.8: Q 3 q si d 6 3 si d 6 3/ 3 si d si d / si Подставляя 3.6 в 3.5, приходим к равенству. 3.7 Y si Q si, из которого следует Y Q. 36 Из последнего равенства c учётом 3.7 находим Y и, подставляя его в 3., получим решение краевой задачи в виде 5 y [ si ] si. 6
34 3 Часть. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ. Классификация уравнений и постановка задач математической физики Большинство физических процессов различной природы моделируется дифференциальными уравнениями в частных производных. Наиболее часто при этом встречаются линейные уравнения второго порядка. Их изучение и составляет предмет математической физики. Дифференциальным уравнением в частных производных называется соотношение между искомой функцией нескольких переменных, её частными производными и независимыми переменными. Для двух независимых переменных и y дифференциальное уравнение в частных производных второго порядка в общем случае имеет вид u u u u u F u,, y. y y y Наивысший порядок частных производных, входящих в уравнение, определяет порядок дифференциального уравнения. Если уравнение содержит производные высших порядков только в первой степени, то оно называется квазилинейным. В случае уравнения -го порядка оно имеет вид; u u u u u Ф u,, y,, f, y. y y y Уравнение называется линейным, если оно содержит искомую функцию и все её производные в первой степени. Линейное дифференциальное уравнение в частных производных второго порядка с двумя независимыми переменными имеет следующий вид u u u u u b b cu f, y.. y y y Коэффициенты линейного уравнения могут зависеть от переменных и y. Тогда говорят, что уравнение. является уравнением с переменными коэффициентами. Если f,y, то уравнение. называется линейным однородным. В противном случае оно будет линейным неоднородным. Всё многообразие уравнений математической физики может быть
35 35 разделено на три класса. Уравнения каждого класса обладают общими свойствами решений. В каждом из этих классов есть простейшее уравнение, называемое каноническим. Принадлежность уравнения к тому или иному классу определяется соотношением между коэффициентами при старших производных. Если в некоторой области плоскости y дискриминант уравнения. >, то говорят, что уравнение. будет в этой области уравнением гиперболического типа. Если в некоторой области плоскости y дискриминант, то в этой области уравнение относится к параболическому типу. Наконец, если в некоторой области или параболы при, или эллипса при 36 36 дах, процессы диффузионного типа и др. Уравнение Лапласа 5 u u. y Это однородное уравнение эллиптического типа. Уравнение Лапласа не содержит времени и y пространственные координаты и описывает стационарные процессы в электрических и магнитных полях, задачи стационарной теплопроводности, установившиеся диффузионные процессы, многие стационарные задачи гидродинамики, прочности, задачи о потенциале поля тяготения и др. Любое дифференциальное уравнение математической физики имеет бесчисленное множество решений. Для получения единственного решения необходимо задание дополнительных условий, которые позволяют однозначно описать конкретный физический процесс. Количество и вид этих условий зависят от характера и порядка производных, входящих в уравнение, от формы области, в которой ищется решение уравнения, от характера взаимодействия рассматриваемого тела или процесса в выделенном теле с окружающей средой. В общем случае дополнительными условиями могут быть начальные и граничные условия. Начальные условия описывают состояние объекта в начальный момент времени. Для уравнения гиперболического типа ставятся два начальных условия соответственно второму порядку производной по времени, входящей в уравнение. Они характеризуют величины отклонений и скоростей точек объекта струны, стержня и др. в начальный момент времени. Для уравнения параболического типа ставится одно начальное условие, что соответствует первому порядку производной по времени если искомая функция в уравнении теплопроводности u, температура в произвольном сечении стержня в любой момент времени t, то начальным условием задаётся распределение температуры по длине стержня в начальный момент времени t. Граничные условия для волнового уравнения если оно описывает, например, поперечные колебания струны конечных размеров характеризуют поведение концов струны в процессе колебаний и зависят от характера их закрепления. Для уравнения теплопроводности стержня граничные условия 5 Л а п л а с Пьер Симон 3 марта 79 5 марта 87 французский астроном и математик.
37 37 имеют существенно различный вид в зависимости от характера теплообмена концов стержня с окружающей средой. Для уравнения эллиптического типа, как и для уравнения параболического типа, также различают разные краевые задачи в зависимости от условий на контуре рассматриваемой области. Итак, постановка задачи математической физики включает задание дифференциального уравнения в частных производных, описывающего исследуемый процесс, а также в общем случае граничных и начальных условий, позволяющих получить единственное решение. Если задача математической физики поставлена корректно, то её решение существует, единственно и устойчиво к малым изменениям исходных данных. Требование непрерывной зависимости решения от исходных данных обусловлено тем, что физические данные, характеризующие начальное состояние системы, определяются, как правило, экспериментально, и всегда с некоторой погрешностью. Поэтому необходима уверенность в том, что малая погрешность в исходных данных будет приводить лишь к малой погрешности в решении, то есть решение задачи не должно существенно зависеть от погрешностей измерений. Понятие корректной постановки задачи, введенное Ж.Адамаром 6, является очень важным в математической физике. Вместе с тем следует заметить, что объективно существуют и являются практически важными и так называемые некорректно поставленные задачи. К ним, например, относятся часто встречающиеся в приложениях обратные задачи задачи идентификации объекта по результатам измерений некоторых его характеристик. Методы решения таких задач отражены в специальной литературе. Ниже рассмотрены решения основных дифференциальных уравнений математической физики различного типа, базирующиеся на одном из наиболее общих методов математической физики методе Фурье разделения переменных. В основе этого метода лежит возможность применения к линейным дифференциальным уравнениям в частных производных принципа суперпозиции наложения частных решений, в соответствии с которым любая линейная комбинация частных решений однородного линейного уравнения также является решением этого уравнения. При этом частные решения отыскиваются в виде произведения функций, каждая из которых зависит только от 6 А д а м а р Жак Саломон 8 декабря октября 963 французский математик.
38 38 одной переменной. Для канонических уравнений математической физики, рассматриваемых ниже в прямоугольной и круговой областях, применение метода Фурье позволяет разделить переменные, то есть свести задачу отыскания функции двух и более переменных, являющейся решением дифференциального уравнения в частных производных, к принципиально более простой задаче отыскания решений независимых друг от друга обыкновенных линейных дифференциальных уравнений. Решение неоднородных уравнений строится при этом с помощью разложения искомых функций в ряды по собственным функциям соответствующей однородной задачи.
39 39. Уравнения гиперболического типа.. Задача о свободных колебаниях струны. Вывод волнового уравнения Струной называется гибкая упругая натянутая нить, не оказывающая сопротивления изгибу. Рассмотрим натянутую струну, которая в начальный момент времени совмещена с отрезком [, ] оси. Пусть концы струны закреплены неподвижно. Если струну тем или иным способом отклонить от первоначального положения, и затем предоставить самой себе, то она начнёт совершать колебания относительно положения равновесия, называемые свободными колебаниями см. рис.9. Требуется найти закон этих колебаний, то есть зависимость перемещения точек струны от времени. Будем предполагать, что струна однородна, то есть имеет постоянную линейную плотность ρ [кг сек /м ] ρ γ g ; γ удельная плотность материала [кг/м 3 ], g 9,8 м/сек ускорение силы тяжести. Примем также, что колебания струны происходят в одной плоскости, и отклонения точек струны от положения равновесия малы настолько, что увеличением длины струны в процессе колебаний можно пренебречь, то есть можно считать, что длина ds элемента M M струны d ds u d d. Допущение о малости колебаний, означает, таким образом, что пренебрегается квадратом угла поворота u по сравнению с единицей, и движение каждой точки струны происходит перпендикулярно оси см. рис.9. Такие колебания будут описываться функцией двух переменных u,. Рис.9.
40 Рассмотрим произвольно выделенный малый элемент струны M M и заменим действие отброшенных участков внешними силами натяжения. Так как струна не обладает изгибной жесткостью, то сила натяжения струны в произвольной точке всегда направлена по касательной к «мгновенному» профилю струны. Тогда условие равновесия сил, действующих на элемент струны, в проекции на ось запишется в виде T cos ϕ T dt cos ϕ dϕ. В силу принятого допущения о малости отклонений точек струны от положения равновесия в процессе колебаний можно принять, что cosϕ cos ϕ d ϕ. Поэтому из уравнения равновесия следует, что dt и T cost, то есть усилие натяжения во всех точках струны будет одинаковым. Вертикальная составляющая сил натяжения уравновешивается поперечными силами инерции. Составляя на основании принципа Даламбера 7 уравнение равновесия сил, действующих на элемент струны, в проекции на ось y, приходим к равенству u Т si ϕ dϕ Tsiϕ ρd,. где ρ d масса, а u ускорение точек элемента струны. Так как ds d и углы ϕ и ϕ dϕ малы, то можно считать, что u, u d, siϕ tgϕ, si ϕ dϕ tg ϕ dϕ. Поэтому T si ϕ dϕ T siϕ T[ tg ϕ dϕ tgϕ]. u d, u, u, T T d. Здесь на основании теоремы Лагранжа 8 о конечных приращениях [8] частное приращение производной u / при переходе от аргу- 7 Д а л а м б е р Жан Лоран 6 ноября 77 9 октября 783 французский механик, физик и математик. 8 Л а г р а н ж Жозеф Луи 5 января 736 апреля 83 французский механик и математик.
41 ментов, к аргументам d, заменено её частным дифференциалом, то есть величиной u,. Подставляя. в. и обозначая T ρ, приводим уравнение. к виду u u. Это уравнение и описывает процесс малых свободных поперечных колебаний струны и называется одномерным волновым уравнением. Это уравнение и его решение впервые были получены Ж.Даламбером в 73 году. Постановка начально-краевой задачи для волнового уравнения Рассмотрим постановку начально-краевой задачи для волнового уравнения на примере задачи о малых свободных поперечных колебаниях струны конечной длины с закреплёнными концами. Требуется решить однородное волновое уравнение u u, [, ], t.3 при однородных граничных условиях u,, u,. и начальных условиях u, u, U, V,.5 где U, V заданные функции, описывающие соответственно отклонения и скорости точек струны в начальный момент времени. 3. Решение однородного волнового уравнения методом разделения переменных методом Фурье В соответствии с методом разделения переменных сначала ищется частное ненулевое решение однородного уравнения.3, удовлетворяющее лишь однородным граничным условиям., в виде произ-
42 ведения двух функций, каждая из которых зависит только от одной переменной: u, X T..6 Подставляя.6 в.3, получим X T X T. Разделив обе части уравнения на X T, приходим к равенству X T..7 X T В этом равенстве при изменении t левая часть, не зависящая от t, остаётся постоянной, поэтому будет постоянной и равная ей правая часть, то есть обе части равенства.7 не зависят от t. С другой стороны, при изменении правая часть равенства, не зависящая от, будет оставаться постоянной, значит, будет постоянной и не зависеть от и равная ей левая часть. Таким образом, обе части равенства.7 не зависят ни от, ни от t. Следовательно, они являются постоянными. Обозначая эту постоянную через μ, её называют постоянной разделения, то есть принимая X T µ, X T получим два независимых обыкновенных линейных однородных дифференциальных уравнения -го порядка T µ T,.8 X µ X..9 Подставляя далее.6 в граничные условия., получим X X.. В результате для определения функции X приходим к задаче на собственные значения.9,. задаче Штурма 9 Лиувилля. Эта задача имеет нулевое тривиальное решение X, не представ- 9 Ш т у р м Жак Шарль Франсуа 9 сентября 83 8 декабря 855 французский математик. Л и у в и л л ь Жозеф марта 89 8 сентября 88 французский математик.
43 3 ляющее физического интереса, так как тогда u,. Однако при некоторых значениях параметра μ, называемых собственными значениями, задача.9,. имеет решения, не равные тождественно нулю. Эти решения называются собственными функциями. Покажем, прежде всего, что ненулевые решения задачи.9,. существуют при μ μ λ, λ >. Характеристическое уравнение, соответствующее уравнению.9 X λ X, имеет вид k λ. Его корни действительны и различны: k, ± λ. Поэтому общее решение уравнения.9 запишется в виде X. λ λ Ce Ce Подставляя его в граничные условия., получим систему однородных линейных алгебраических уравнений C C, λ λ e C e C, которая имеет единственное нулевое решение C C. Соответственно задача.9,. будет иметь только нулевое решение X. Пусть μ . Тогда корни характеристического уравнения X λ X. будут мнимыми: k, ± λ ± λi. Поэтому частные линейно независимые решения будут X cosλ, X si λ, и общее решение уравнения. запишется в виде X C cosλ C si λ..
44 Из первого граничного условия. получаем C, а из второго граничного условия следует C si λ..3 Если C, то опять получим нулевое решения X. Поэтому, чтобы существовало нетривиальное решение задачи, необходимо принять si λ.. Из уравнения. следует λ, где ±, ±. так как λ. Поэтому собственные значения параметра для задачи.9,. будут λ.5 так как собственные значения будут различными для разных, то им приписывается соответствующий индекс. Соответствующие им собственные функции с точностью до постоянного множителя C определяются по формуле X si..6 Здесь уместно объяснить причину, по которой выше было принято рассматривать только положительные значения параметра λ. Это было сделано потому, что при отрицательных значениях λ или номера будут получаться собственные функции, отличающиеся лишь постоянным множителем. Заметим, что собственные функции.6 ортогональны на отрезке [, ]. С учетом.5 уравнение.8 запишется в виде T T.7 Его общее решение: t t T A cos B si..8 Подставляя.6 и.8 в.6 и суммируя частные решения линейного однородного уравнения.3, получим t t u, A cos B si si.9
45 5 Произвольные постоянные A и B находим далее из начальных условий. Подстановка.9 в.5 приводит к равенствам u, U A si,. u, V B si.. Если функции U и V удовлетворяют условиям Дирихле, то произвольные постоянные A и B могут быть определены как коэффициенты Фурье для соответствующих функций при разложении их в ряды Фурье по синусам на промежутке [, ], равном длине струны. Тогда A U si d,. B V si d..3 Выражение.9 с учетом. и.3 и даёт окончательное решение задачи о малых собственных поперечных колебаниях струны. В полученном решении разные значения соответствуют различным собственным формам колебаний струны. Функцию u, A t cos B t si si введением вспомогательного угла ϕ rctg A B легко преобразовать к виду u, t F si si t ϕ,. где F A B. Из. следует, что все точки струны совершают гармонические колебания относительно положения равновесия с одинаковыми частотами ω и амплитудой F si, зависящей от продольной координаты точки струны. Такие колебания называются стоячими волнами. При этом максимальное отклонение от положения
46 6 равновесия будет достигаться при si ±, то есть в точках с абсциссами k, k. на отрезке [, ]. Точки, в которых отклонения достигают максимума, называются пучностями. Но при колебаниях струны имеются и неподвижные точки, которые называются узлами стоячей волны. Они определяются из условия si. Таких точек на отрезке [, ] будет с абсциссами k, k. Первые три формы колеблющейся струны в разные моменты времени показаны на рис.. Рис.. Результирующее отклонение u, произвольной точки струны, как следует из.9, равно сумме отклонений, соответствующих разным формам колебаний. Частоты колебаний ω называются собственными частотами. Наименьшая собственная частота колебаний соответствует и равна T ω. ρ Она соответствует основному тону колебаний струны. Как видно, частота основного тона колебаний тем выше, чем сильнее натянута струна и чем она короче и легче. Высшие тона колебаний называются обертонами. Пример. Найти закон колебания струны длиной, если в начальный момент струне придана форма кривой u, 8 а затем струна отпущена без начальной скорости. Струна закреплена на концах. Внешние силы отсутствуют. Решение. Задача сводится к решению однородного волнового уравнения. при однородных граничных условиях.5 и начальных условиях
47 7 u, u. 5 8 Для рассматриваемого случая, очевидно, B, так как согласно.5 V. Подставляя в. U, 8 после двукратного интегрирования по частям находим A..6 3 Подстановка.6 в.9 с учетом B приводит к решению задачи в виде t u, cos si Продольные колебания стержня Стержнем называют тело, размеры поперечного сечения которого малы по сравнению с его длиной. Как известно, стержень является основным расчётным объектом в сопротивлении материалов. Будем рассматривать призматический стержень постоянного поперечного сечения с прямолинейной осью. Если стержень предварительно растянут или сжат осевыми силами, и в момент времени t действие сил мгновенно прекращается, то он будет совершать свободные собственные продольные колебания. Будем предполагать, что при этом сечения, перпендикулярные к продольной оси стержня, оставаясь плоскими, будут смещаться только вдоль оси абсцисс, совпадающей с продольной осью стержня см. рис.. Предполагаем также, что стержень однородный, то есть выполнен из материала с постоянной линейной плотностью ρ. Рис.. Пусть u, [м] продольное перемещение поперечного сечения
48 8 стержня с абсциссой в момент времени t, E модуль упругости материала стержня [Па], F площадь поперечного сечения стержня [м ], его длина [м]. Относительное удлинение деформация стержня в сечении с абсциссой в момент времени t равно u, u, u ε im. Внутренние нормальные силы определяются по закону Гука и равны: u в сечении : N σ F EεF EF ; в сечении d : u u u dn EF u d EF d. N Следовательно, равнодействующая внутренних нормальных сил упругости, приложенных к элементу стержня, равна u u u u N dn N EF d EF EF d. Эта сила уравновешивается возникающими при продольных колебаниях силами инерции ρ Fd u. Приравнивая в соответствии с принципом Даламбера сумму сил, действующих на выделенный элемент стержня, нулю: u u EF d ρ Fd,.8 получим уравнение продольных колебаний стержня u u,.9 где теперь E ρ скорость распространения упругих волн в материале стержня, скорость звука в материале [м/сек]. Как видно, уравнение малых свободных продольных колебаний стержня совпадает по форме записи с уравнением малых поперечных Г у к Роберт 8 июля марта 73 английский физик.
49 9 колебаний струны.. Различие между этими задачами будет проявляться в постановке граничных условий. Ограничимся случаем консольного защемлённого стержня рис.. Рис.. Очевидно, на левом конце стержня u..3 Так как на свободном конце стержня внешних сил нет, то равнодействующая внутренних нормальных сил упругости N EF[ u, ] должна быть равна нулю, откуда следует u. 3 Как видно, в отличие от задачи о свободных поперечных колебаниях закреплённой по концам струны.3.5, граничные условия теперь являются «смешанными», то есть ставятся на функцию и её производную. Начальными условиями определяются продольные перемещения и скорости поперечных сечений стержня в момент времени t : u, u, f, ϕ,.3 где f и ϕ заданные функции. Найдём решение начально-краевой задачи.9.3 методом разделения переменных. Как и выше, представляя ненулевое частное решение уравнения.9 в виде.6, после обычных преобразований, характерных для метода разделения переменных, получим уравнения.8 и.9. Подставляя.6 в граничные условия.3,.3, находим X X..33 Таким образом, для определения функции X теперь приходим к задаче на собственные значения. 33. Общее решение уравнения. имеет вид X C si λ C cosλ.
Преобразование Фурье с примерами решения и образцами выполнения
Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.
Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(х) называется функция (*)
где К(х, w) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).
Интеграл Фурье
Всякая функция f(x), которая на отрезке [— l, l] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом (1)
Коэффициенты аn и bn ряда (1) определяются по формулам Эйлера—Фурье:
(2)
Ряд в правой части равенства (1) можно записать в иной форме. С этой целью внесем в него из формул (2) значения коэффициентов аn и bn, подведем под знаки интегралов cos 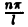
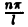
(3)
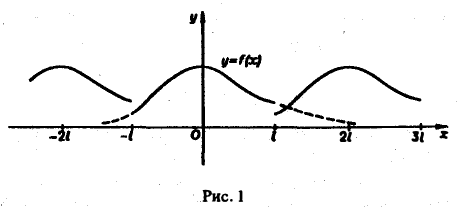
Если функция f(x) первоначально была определена на интервале числовой оси, большем, чем отрезок [-l, l] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-l, l] и продолжит ее на всю числовую ось как периодическую функцию с периодом 2l (рис. 1).
Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при l → +∞. При этом естественно потребовать выполнения следующих условий:
1, f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;
2. функция f(x) абсолютно интегрируема на всей числовой оси,
При выполнении условия 2 первое слагаемое правой части равенства (3) при l → +∞ стремится к нулю. В самом деле,
Попытаемся установить, во что перейдет в пределе при l → +∞ сумма в правой части (3). Положим
так, что 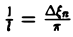
В силу абсолютной сходимости интеграла эта сумма при больших l мало отличается от выражения
которое напоминает интегральную сумму для функции переменного ξ
составленную для интервала (0, + ∞) изменения Поэтому естественно ожидать, что при l → +∞ ( 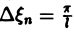
С другой стороны, при l → +∞ (х фиксировано) из формулы (3) вытекает, что
и мы получаем равенство
(7)
Достаточное условие справедливости формулы (7) выражается следующей теоремой.
Теорема:
Если функция f(x) абсолютно интегрируема на всей числовой оси — ∞
При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции f(x), значение интеграла в правой части (7) равно
Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралам Фурье.
Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде (8)
Функции а( ξ ), b( ξ ) являются аналогами соответствующих коэффициентов Фурье an и bn 2π-периодической функции, но последние определены для дискретных значений п, в то время как а( ξ ), b( ξ ) определены для непрерывных значений ξ ∈ (— ∞, + ∞).
Комплексная форма интеграла Фурье
Предполагая f(x) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл
Этот интеграл равномерно сходится для — ∞
и потому представляет собой непрерывную и, очевидно, нечетную функцию от ξ. Но тогда
С другой стороны, интеграл
есть четная функция переменной так что
Поэтому интегральную формулу Фурье можно записать так:
на мнимую единицу i и прибавим к равенству (10). Получим
откуда, в силу формулы Эйлера (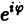
(11)
Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по ξ понимается в смысле главного значения по Коши:
Преобразование Фурье. Косинус- и синус-преобразования Фурье
Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.
Определение:
называется преобразованием Фурье функции f(x) (спектральной функцией).
Это — интегральное преобразование функции f(x) на интервале (- ∞ ,+ ∞) с ядром
Используя интегральную формулу Фурье
Это так называемое обратное преобразование Фурье, дающее переход от F( ξ ) к f(x). Иногда прямое преобразование Фурье задают так:
Тогда обратное преобразование Фурье определится формулой
Преобразование Фурье F( ξ ) функции f(х) определяют также следующим образом:
Тогда, в свою очередь,
При этом положение множителя 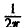
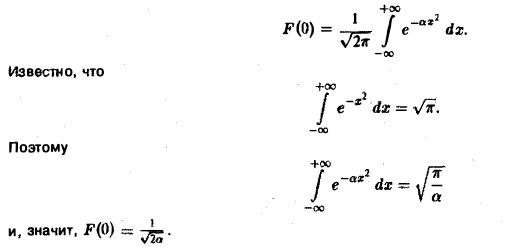
Пример:
Найти преобразование Фурье функции
Это равенство допускает дифференцирование по ξ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда ξ принадлежит любому конечному отрезку):
Интегрируя по частям, будем иметь
Внеинтегральное слагаемое обращается в нуль, и мы получаем
(С — постоянная интегрирования). Полагая в (4) ξ = 0, найдем С —F(0). В силу (3) имеем
В частности, для
Пример:
Разряд конденсатора через сопротивление. Рассмотрим функцию
Для спектральной функции F( ξ ) получаем
Условие абсолютной интегрируемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как f(x) = 1. f(x) = x 3 , f(х) = cosx, f(х) = е х , для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.
Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| → + ∞ (как в примерах 1 и 2).
Косинус- и синус-преобразования Фурье
Используя формулу косинуса, разности, перепишем интегральную формулу Фурье
в следующем виде:
Пусть f(x) — четная функция. Тогда
так что из равенства (5) имеем
(6)
В случае нечетной f(x) аналогично получаем
(7)
Если f(х) задана лишь на (0, + ∞), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным.
Определение:
называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x)
Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc( ξ ). Иными словами, функции f и Fc являются взаимными косинус-преобразованиями.
Определение:
называется синус-преобразованием Фурье функции f(x).
Из (7) получаем, что для нечетной функции f(х)
т.е. f и Fs являются взаимными синус-преобразованиями.
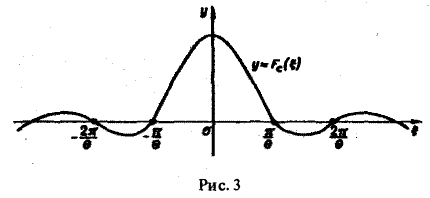
Пример:
Прямоугольный импульс. Пусть f(t) — четнaя функция, определенная следующим образом:
Воспользуемся полученным результатом для вычисления интеграла
В силу формулы (9) имеем
В точке t = 0 функция f(t) непрерывна и равна единице.
Поэтому из (12′) получим
Амплитудный и фазовый спектры интеграла Фурье
Пусть периодическая с периодом 2π функция f(х) разлагается в ряд Фурье
Это равенство можно записать в виде
где Cn = 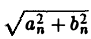
Для непериодической функции f(x), заданной на (- ∞, + ∞), при определенных условиях оказывается возможным представить ее интегралом Фурье
осуществляющим разложение этой функции по всем частотам 0
(прямое преобразование Фурье функции f(х)).
называется амплитудным спектром, а функция
(0 — фазовым спектром функции f(x).
Амплитудный спектр A (ξ) служит мерой вклада частоты ξ в функцию f(х).
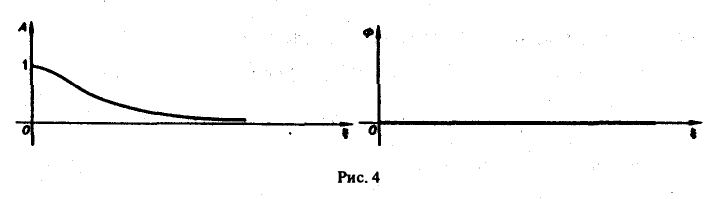
Пример:
Найти амплитудный и фазовый спектры функции
Находим спектральную функцию
Графики этих функций изображены на рис. 4.
Свойства преобразования Фурье
1, Линейность. Если F( ξ ) и G( ξ ) — преобразования Фурье функций f(х) и g(х) соответственно, то при любых постоянных а и β преобразованием Фурье функции а f(х) + β g(х) будет функция a F( ξ ) + βG( ξ ).
Пользуясь свойством линейности интеграла, имеем
Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через 
Если F( ξ ) есть преобразование Фурье абсолютно интегрируемой на всей числовой оси функции f(х), то F( ξ ) ограничена при всех ξ ∈ (— ∞, + ∞).
Пусть функция f(х) абсолютно интегрируема на всей оси — ∞
— преобразование Фурье функции f(х). Тогда
Задача:
Пусть f(x) — функция, допускающая преобразование Фурье, h — действительное число. Функция fh(x) = f(x-h) называется сдвигом функции f(x). Пользуясь определением преобразования Фурье, показать, что
Задача:
Пусть функция f(x) имеет преобразование Фурье F( ξ ), h — действительное число. Показать, что
3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция f(х) имеет производную f'(х), также абсолютно интегрируемую на всей оси Ох, так что f(х) стремится к нулю при |х| —► + ∞. Считая f'(х) гладкой функцией, запишем
Интегрируя по частям, будем иметь
Внеинтегральное слагаемое обращается в нуль (так как f(х) → 0 при |х| → + ∞), и мы получаем (1)
Таким образом, дифференцированию функции f(х) отвечает умножение ее образа Фурье 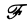
Если функция f(х) имеет гладкие абсолютно интегрируемые производные до порядка m включительно и все они, как и сама функция f(х), стремятся к нулю при |x| → + ∞, то, интегрируя по частям нужное число раз, получим
Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину iξ и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.
Так как преобразование Фурье 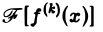
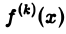
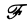
Из этой оценки следует: чем больше функция f(х) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при | ξ | → + ∞.
Замечание:
Условие 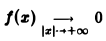
4. Связь между скоростью убывания функции f(x) при |х| → + ∞ и гладкостью ее преобразования Фурье. Предположим, что не только f(x), но и ее произведение хf(х) является абсолютно интегрируемой функцией на всей оси Ох. Тогда преобразование Фурье
функции f(x) будет дифференцируемой функцией.
Действительно, формальное дифференцирование по параметру ξ подынтегральной функции приводит к интегралу
который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и
т. е. операция умножения f(х) на аргумент х переходит после преобразования Фурье в операцию
Если вместе с функцией f(х) абсолютно интегрируемыми на всей оси Ох являются функции хf(х)…..х m f(х), то процесс дифференцирования можно продолжить.
Получим, что функция F( ξ ) = 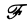
Таким образом, чем быстрее функция f(х) убывает при |х| → + ∞, тем более гладкой получается функция F( ξ ) = 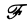
Теорема:
О свертке. Пусть F1( ξ ) и F2( ξ ) — преобразования Фурье функций f1(x) и f2(x) соответственно. Тогда
причем двойной интеграл в правой части сходится абсолютно.
Положим х + у = т, так что у = т — х. Тогда будем иметь
или, меняя порядок интегрирования,
называется сверткой функций f(x) и f2(x) и обозначается символом 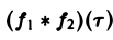
Отсюда видно, что преобразование Фурье свертки функций f1(x) и f2(x) равно умноженному на 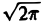
Замечание:
Нетрудно установить следующие свойства свертки:
Приложения преобразования Фурье
1, Пусть 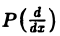
(аo, a1,… ,ат = const). Используя формулу для преобразования Фурье производных функции у(х), находим
Рассмотрим дифференциальное уравнение
где 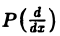
Предположим, что искомое решение у(х) имеет преобразование Фурье y(ξ), а функция f(x) имеет преобразование f( ξ ). Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси Oξ относительно y(ξ)
так что формально
где символ 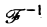
Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида
Они не являются абсолютно интегрируемыми на оси — ∞
(а = const), при начальных условиях
Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение φ(х) точек струны, а начальные скорости отсутствуют.
Поскольку пространственная переменная х изменяется в пределах от — ∞ до + ∞, подвергнем уравнение и начальные условия преобразованию Фурье по переменной х. Будем предполагать, что
1) функции u(z, t) и φ(x) — достаточно гладкие и стремятся к нулю при \х\ → + ∞ и ∀t ≥ О настолько быстро, что существуют преобразования Фурье
2) допустимы операции дифференцирования, так что
Умножая обе части (2) на 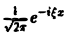
а из начальных условий (3) найдем
Таким образом, применяя к задаче (2)-(3) преобразование Фурье, приходим к задаче Коши (8)—(10) для обыкновенного дифференциального уравнения, где ξ — параметр. Решением уравнения (8) является функция
Из условий (9) и (10) находим, что С1( ξ ) = φ( ξ ). C2( ξ ) = 0, так что v( ξ, t) = φ( ξ )cos aξt. Применяя обратное преобразование Фурье, получим
Это частный случай формулы Даламбера решения задачи (2)-(3).
2. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т. е. уравнений, в которых неизвестная функция входит под знак интеграла.
Рассмотрим, например, уравнение
где φ(х) — искомая функция. Записав (1) в виде
замечаем, что левую часть (2) можно рассматривать как преобразование Фурье функции φ(х), так что (2) равносильно следующему равенству:
Тогда по формуле обращения
Функция 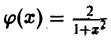
Понятие о многомерном преобразовании Фурье
Преобразование Фурье:
Многомерным преобразованием Фурье абсолютно интегрируемой функции f(х1, х2,…, хb) называется функция
символ 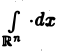
Свойства многомерного преобразования аналогичны соответствующим свойствам преобразования Фурье функции одной переменной. В специальном случае, когда
Дополнение к преобразованию Фурье


Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://lfirmal.com/preobrazovanie-fure/