С 32 простейшие тригонометрические уравнения

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

1. Корни уравненияcosx=a.

При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

1. Какие уравнения называют простейшими тригонометрическими?
2. Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
3. Выведите формулы решения простейших тригонометрических уравнений.
4. Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Простейшие тригонометрические уравнения (задание 5) и неравенства

\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad \mathrm\,x=b,\quad \mathrm\,x=b\) , которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb\) .

Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\) ).

Рассмотрим несколько примеров:

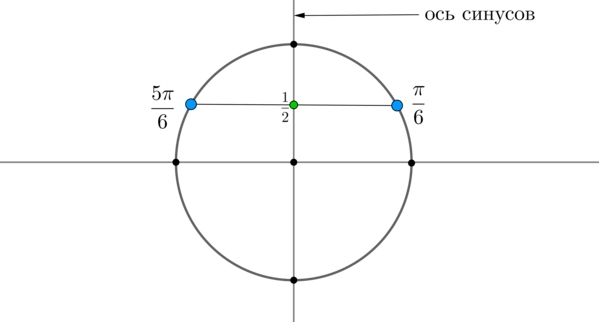
Пример 1. Решить уравнение \(\sin x=\dfrac12\) .

Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\) , где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).

Таким образом, решением являются \(x_1=\dfrac<\pi>6+2\pi n,\ x_2=\dfrac<5\pi>6+2\pi n, \ n\in \mathbb\) .

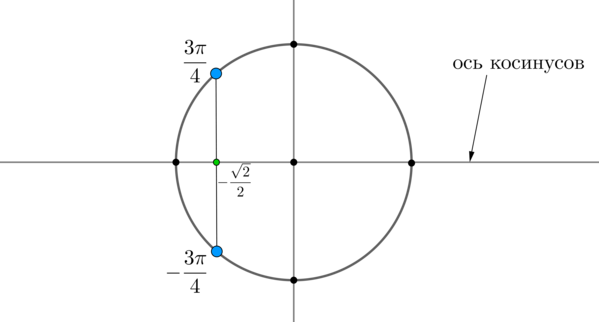
Пример 2. Решить уравнение \(\cos x=-\dfrac<\sqrt2><2>\) .

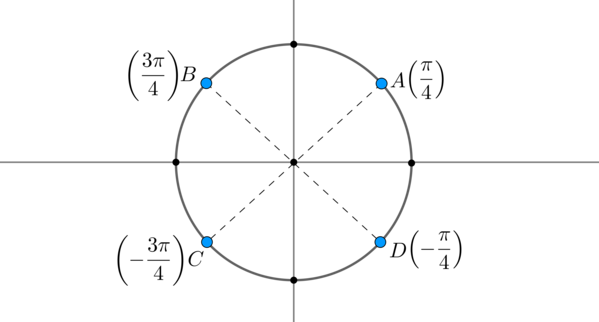
Найдем на оси косинусов точку \(-\dfrac<\sqrt2><2>\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac<\sqrt2><2>\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<3\pi>4\) и \(-\dfrac<3\pi>4\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число.

Таким образом, решением являются \(x_1=\dfrac<3\pi>4+2\pi n,\ x_2=-\dfrac<3\pi>4+2\pi n, \ n\in \mathbb\) .

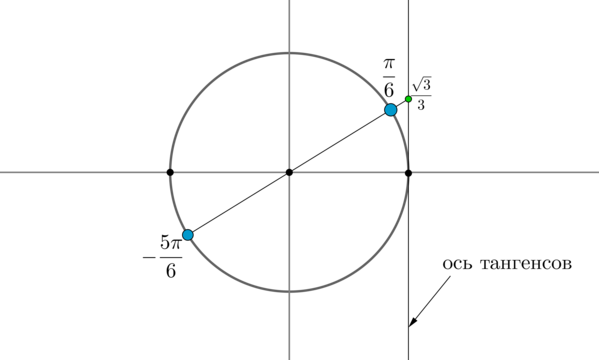
Пример 3. Решить уравнение \(\mathrm\,x=\dfrac<\sqrt3>3\) .

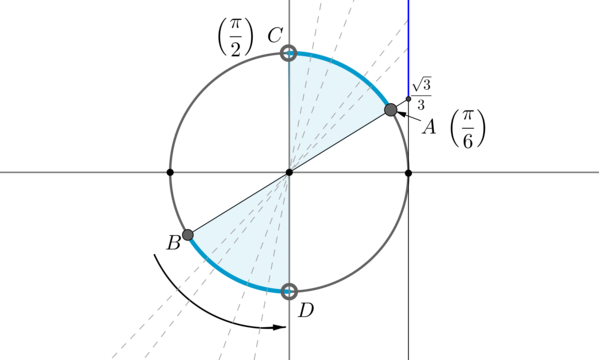
Найдем на оси тангенсов точку \(\dfrac<\sqrt3>3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac<\sqrt3>3\) .Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

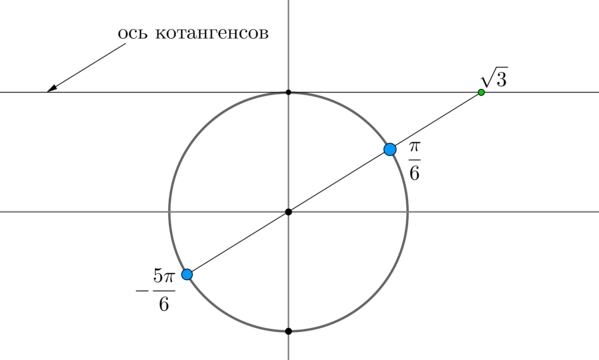
Пример 4. Решить уравнение \(\mathrm\,x=\sqrt3\) .

Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin \hline \text <Уравнение>& \text <Ограничения>& \text<Решение>\\ \hline &&\\ \sin x=a & -1\leq a\leq 1 & \left[ \begin \begin &x=\arcsin a+2\pi n\\ &x=\pi -\arcsin a+2\pi n \end \end \right. \ \ , \ n\in \mathbb\\&&\\ \hline &&\\ \cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\, x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\,x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline \end\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb\) .

\(\blacktriangleright\) Любые уравнения вида \(\mathrm\,\big(f(x)\big)=a\) , (где \(\mathrm\) — одна из функций \(\sin, \ \cos, \ \mathrm,\ \mathrm\) , а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\) .

Пример 5. Решить уравнение \(\sin<(\pi x+\dfrac<\pi>3)>=1\) .

Сделав замену \(t=\pi x+\dfrac<\pi>3\) , мы сведем уравнение к виду \(\sin t=1\) . Решением данного уравнения являются \(t=\dfrac<\pi>2+2\pi n, n\in\mathbb\) .

Теперь сделаем обратную замену и получим: \(\pi x+\dfrac<\pi>3=\dfrac<\pi>2+2\pi n\) , откуда \(x=\dfrac16+2n,\ n\in\mathbb\) .

Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac<2\pi>n,\ n\in\mathbb\) , где \(\alpha\) — один из этих углов.

Рассмотрим данную ситуацию на примере:

Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac<\pi>4+2\pi n, \ x_2=\pm \dfrac<3\pi>4+2\pi n, \ n\in\mathbb\) . Отметим эти точки на окружности:

Заметим, что длины дуг \(\buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over\) равны \(\dfrac<\pi>2\) , то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac<\pi>4+\dfrac<\pi>2n, \ n\in\mathbb\) .

где \(\lor\) — один из знаков \(\leq,\ ,\ \geq\) .

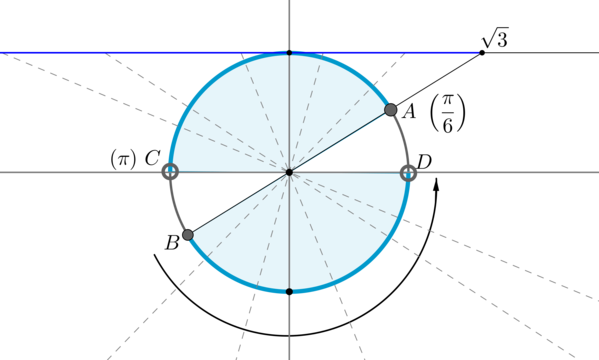
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\) .

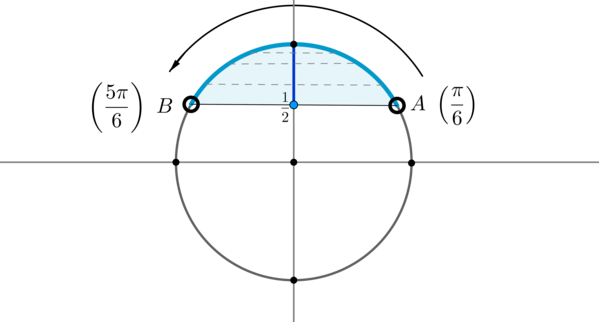
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, синус которых больше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>6\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>6\) , но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>6\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>6;\dfrac<5\pi>6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac<\pi>6+2\pi n;\dfrac<5\pi>6+2\pi n\right), n\in\mathbb\) , т.к. у синуса период \(2\pi\) .

Пример 8. Изобразить на окружности множество решений неравенства \(\cos x .

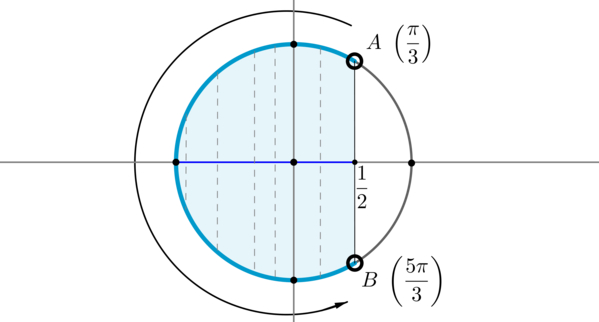
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, косинус которых меньше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>3\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>3\) , но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>3\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>3;\dfrac<5\pi>3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac<5\pi>3+2\pi n;-\dfrac<\pi>3+2\pi n\right), n\in\mathbb\) , т.к. у косинуса период \(2\pi\) .

Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm\, x \geq \dfrac<\sqrt<3>>3\) .

Для начала отметим на окружности корни уравнения \(\mathrm\, x = \dfrac<\sqrt<3>>3\) . Это точки \(A\) и \(B\) . Все точки, тангенс которых больше или равен \(\dfrac<\sqrt<3>>3\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac<\pi>2\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\dfrac<\pi>2\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\dfrac<\pi>2\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\dfrac<\pi>2+\pi n\Big), n\in\mathbb\) , т.к. у тангенса период \(\pi\) .

Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm\, x \leq \sqrt<3>\) .

Для начала отметим на окружности корни уравнения \(\mathrm\, x = \sqrt<3>\) . Это точки \(A\) и \(B\) . Все точки, котангенс которых меньше или равен \(\sqrt<3>\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\pi\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\pi\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\pi+\pi n\Big), n\in\mathbb\) , т.к. период котангенса \(\pi\) .

Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.

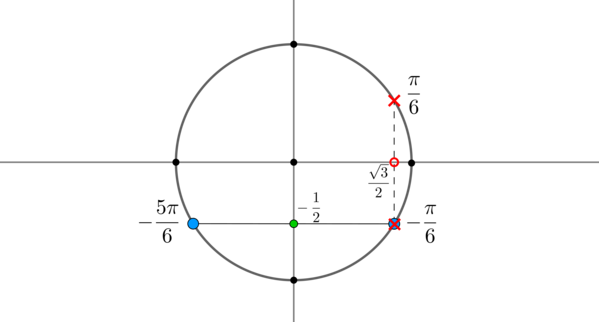
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\) , если \(\cos x\ne \dfrac<\sqrt3>2\) .

В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.

Решением первого уравнения являются \(x_1=-\dfrac<\pi>6+2\pi n,\ x_2=-\dfrac<5\pi>6+2\pi n,\ n\in \mathbb\) , решением второго являются \(x\ne \pm \dfrac<\pi>6+2\pi n,\ n\in\mathbb\) . Отметим эти точки на окружности:

Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac<\pi>6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac<5\pi>6+2\pi n, n\in \mathbb\) .

Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin &\sin<(\alpha+\pi n)>=\begin \sin \alpha, \text <при >n — \text< четном>\\ -\sin \alpha, \text <при >n — \text < нечетном>\end\\ &\cos<(\alpha+\pi n)>=\begin \cos \alpha, \text <при >n — \text< четном>\\ -\cos \alpha, \text <при >n — \text <нечетном>\end\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\sin<\left(\alpha+\dfrac<\pi>2\right)>=\cos\alpha\\ &\cos<\left(\alpha+\dfrac<\pi>2\right)>=-\sin \alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha \end\]

Пример 12. Решить систему \(\begin \cos x=\dfrac12\\ \sin x+\cos x>0\end\)

Решением уравнения являются \(x_1=\dfrac<\pi>3+2\pi n,\ x_2=-\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) . Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:

\(\sin x_1+\cos x_1=\dfrac<\sqrt3>2+\dfrac12>0\) , следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac<\sqrt3>2+\dfrac12 , следовательно, корень \(x_2\) нам не подходит.

Таким образом, решением системы являются только \(x=\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) .

Алгебраический способ.

Пример 13. Найти корни уравнения \(\sin x=\dfrac<\sqrt2>2\) , принадлежащие отрезку \([0;\pi]\) .

Решением уравнения являются \(x_1=\dfrac<\pi>4+2\pi n, \ x_2=\dfrac<3\pi>4 +2\pi n, \ n\in\mathbb\) . Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq x_2\leq\pi\) :

\(0\leq \dfrac<\pi>4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\) . Таким образом, единственное целое значение \(n\) , удовлетворяющее этому неравенству, это \(n=0\) . При \(n=0\) \(x_1=\dfrac<\pi>4\) — входит в отрезок \([0;\pi]\) .

Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac<3\pi>4\) .

Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:

Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\) .

Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\) . Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\) , то есть нечетное число.

Пример: Решить уравнение \(3x+5y=2\) . Т.к. \(НОД(3,5)=1\) , то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\) :

Число \(\dfrac<2-2y>3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\) : \(0\) , \(1\) или \(2\) .
Если \(y\) при делении на \(3\) имеет остаток \(0\) , то оно записывается как \(y=3p+0\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2\cdot 3p>3=\dfrac23-2p\ne \text<целому числу>\]

Если \(y\) при делении на \(3\) имеет остаток \(1\) , то оно записывается как \(y=3p+1\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2(3p+1)>3=-2p=\text<целому числу>\]

Значит, этот случай нам подходит. Тогда \(y=3p+1\) , а \(x=\dfrac<2-2y>3-y=-5p-1\) .

Ответ: \((-5p-1; 3p+1), p\in\mathbb\) .

Перейдем к примеру:

Пример 14. Решить систему \[\begin \sin \dfrac x3=\dfrac<\sqrt3>2\\[3pt] \cos \dfrac x2=1 \end\]

Решим первое уравнение системы:

\[\left[ \begin \begin &\dfrac x3=\dfrac<\pi>3+2\pi n\\[3pt] &\dfrac x3=\dfrac<2\pi>3 +2\pi m \end \end \right.\quad n,m\in\mathbb \quad \Leftrightarrow \quad \left[ \begin \begin &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end \end \right.\quad n,m\in\mathbb\]

Решим второе уравнение системы:

\[\dfrac x2=2\pi k, k\in\mathbb \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb\]

Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\) , при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\) :

\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]

Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\) , то данное уравнение не имеет решений в целых числах.

Найдем целые \(m\) и \(k\) , при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\) :

\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]

Данное уравнение имеет решение в целых числах. Выразим \(k=\frac<3m+1>2=m+\frac2\) .

Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\) .
Если \(m=2p+0\) , то \(\frac2=\frac<2p+1>2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\) , то \(\frac2=\frac<2p+1+1>2=p+1= \) целому числу.

Значит, \(m=2p+1\) , тогда \(k=3p+2\) , \(p\in\mathbb\) .

Подставим либо \(m\) , либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb\) .

Простейшие тригонометрические уравнения. Часть 1

Простейшими называются тригонометрические уравнения следующих четырёх видов:

Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших. К сожалению, на этом заключительном стандартном шаге школьники часто допускают ошибки, что ведет к потере баллов на ЕГЭ. Именно поэтому так важна данная тема.

Существуют два подхода к решению простейших тригонометрических уравнений.
Первый подход — бессмысленный и тяжёлый. Следуя ему, надо выучить по шпаргалке общие формулы, а также все частные случаи. Польза от этого столь же невелика, как от зубрежки шестнадцати строк заклинаний на непонятном языке. Мы отказываемся от такого подхода раз и навсегда.

Второй подход — логический и наглядный. Для решения простейших тригонометрических уравнений мы пользуемся тригонометрическим кругом и определениями тригонометрических функций.

Уравнения и

Напомним, что — абсцисса точки на единичной окружности, соответствующей углу , а — её ордината.

Из определения синуса и косинуса следует, что уравнения и имеют решения только при условии .

Абитуриент, будь внимателен! Уравнения или решений не имеют!

Начнём с самых простых уравнений.

. .
Мы видим, что на единичной окружности имеется лишь одна точка с абсциссой 1:

Эта точка соответствует бесконечному множеству углов: . Все они получаются из нулевого угла прибавлением целого числа полных углов (т. е. нескольких полных оборотов как в одну, так и в другую сторону).

Следовательно, все эти углы могут быть записаны одной формулой:

Это и есть множество решений данного уравнения. Напоминаем, что — это множество целых чисел.

Снова видим, что на единичной окружности есть лишь одна точка с абсциссой :

Эта точка соответствует углу и всем углам, отличающихся от на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой:

. .
Отмечаем на тригонометрическом круге единственную точку с ординатой :

И записываем ответ:

Обсуждать тут уже нечего, не так ли? 🙂

Можете, кстати, записать ответ и в другом виде:

Это — дело исключительно вашего вкуса.
Заодно сделаем первое полезное наблюдение. Чтобы описать множество углов, отвечающих одной-единственной точке тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .

На тригонометрическом круге имеются две точки с ординатой 0:

Эти точки соответствуют углам Все эти углы получаются из нулевого угла прибавлением целого числа углов (т. е. с помощью нескольких полуоборотов в обе стороны). Таким образом,

Точки, лежащие на концах диаметра тригонометрического круга, мы будем называть диаметральной парой.

Точки с абсциссой 0 также образуют диаметральную пару, на сей раз вертикальную:

Все углы, отвечающие этим точкам, получаются из — прибавлением целого числа углов (полуоборотов):

Теперь мы можем сделать и второе полезное наблюдение.

Чтобы описать множество углов, отвечающих диаметральной паре точек тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .

Переходим к следующему этапу. Теперь в правой части будет стоять табличное значение синуса или косинуса (отличное от 0 или ). Начинаем с косинуса.

Имеем вертикальную пару точек с абсциссой :

Все углы, соответствующие верхней точке, описываются формулой (вспомните первое полезное наблюдение!):

Аналогично, все углы, соответствующие нижней точке, описываются формулой:

Обе серии решений можно описать одной формулой:

Остальные уравнения с косинусом решаются совершенно аналогично. Мы приводим лишь рисунок и ответ.

Теперь рассмотрим уравнения с синусом. Тут ситуация немного сложнее.

Имеем горизонтальную пару точек с ординатой :

Углы, отвечающие правой точке:

Углы, отвечающие левой точке:

Описывать эти две серии одной формулой никто не заставляет. Можно записать ответ в таком виде:

Тем не менее, объединяющая формула существует, и её надо знать. Выглядит она так:

На первый взгляд совершенно не ясно, каким образом она дает обе серии решений. Но давайте посмотрим, что получается при чётных . Если , то

Мы получили первую серию решений . А если — нечетно, , то

Это вторая серия .

Обратим внимание, что в качестве множителя при обычно ставится правая точка, в данном случае .

Остальные уравнения с синусом решаются точно так же. Мы приводим рисунок, запись ответа в виде совокупности двух серий и объединяющую формулу.

На этом с синусом и косинусом пока всё. Переходим к тангенсу.

Линия тангенсов.

Начнём с геометрической интерпретации тангенса — так называемой линии тангенсов. Это касательная к единичной окружности, параллельная оси ординат (см. рисунок).

Из подобия треугольников и имеем:

Мы рассмотрели случай, когда находится в первой четверти. Аналогично рассматриваются случаи, когда находится в остальных четвертях. В результате мы приходим к следующей геометрической интерпретации тангенса.

Тангенс угла равен ординате точки , которая является точкой пересечения линии тангенсов и прямой , соединяющей точку с началом координат.

Вот рисунок в случае, когда находится во второй четверти. Тангенс угла отрицателен.

Уравнение

Заметим, что тангенс может принимать любые действительные значения. Иными словами, уравнение имеет решения при любом .

.
Имеем диаметральную горизонтальную пару точек:

Эта пара, как мы уже знаем, описывается формулой:

Имеем диаметральную пару:

Вспоминаем второе полезное наблюдение и пишем ответ:

Остальные уравнения с тангенсом решаются аналогично. Мы приводим лишь рисунки и ответы.

На этом заканчиваем пока и с тангенсом.

Уравнение нет смысла рассматривать особо. Дело в том, что:
уравнение равносильно уравнению ;

при уравнение равносильно уравнению .

Впрочем, существует также и линия котангенсов, но. . . Об этом мы вам расскажем на занятиях 🙂

Итак, мы разобрали простейшие тригонометрические уравнения, содержащие в правой части табличные значения тригонометрических функций. Именно такие задачи встречаются в части В вариантов ЕГЭ.

А что делать, например, с уравнением ? Для этого надо сначала познакомиться с обратными тригонометрическими функциями. О них мы расскажем вам в следующей статье.