С 32 решение задач с помощью систем уравнений

Решение задач с помощью систем уравнений второй степени. 9-й класс

Разделы: Математика

Класс: 9

Цели урока:

1. Обучение составлению системы уравнений по условию задачи.
2. Повышение интереса к решению текстовых задач.

Ход урока

I. Устный счет (8 мин)

Является ли решением уравнения х+2у=5 пара чисел: а) (0;1) б) (3;-1) в) (-1;3)

1. Является ли решением системы уравнений ,

пара чисел: а) х=1, у=6 б)х=3, у=2

2. Решите систему уравнений:

3. Определите степень уравнения:

• А) х-у-1,2=0
• Б)
• В)
• Г)

II. Изучение нового материала (10 мин)

При решении задач можно вводить две переменные и составлять систему уравнений.

Решить задачу двумя способами: «Гипотенуза прямоугольного треугольника равна 13 см. Найдите его катеты, если известно, что один из них на 7 см больше другого».

1 способ— с помощью одной переменной.

Пусть один катет прямоугольного треугольника равен х см, а второй катет – х+7 см. Используя теорему Пифагора, составим уравнение:

корень х=-12 не удовлетворяет условию х>0.

Один катет равен 5 см, второй 12 см

2 способ— с помощью введения двух переменных.

Пусть первый катет х см, второй катет у см (х>0, у>0)

,

,

,

у1=5, у2=-12 (не удовл. условию)

если у=5, то х=7+5=12

один катет равен 5 см, второй катет 12 см

Ответ: 12 см, 5 см

III. Закрепление нового материала (10 мин)

Решение задач:

1. Прямоугольный газон обнесён изгородью, длина которой 30 м. Площадь газона 56 м². Найдите длины сторон газона?

Решение: пусть х м –длина газона, у-ширина газона.

,

,

Ответ: 7 см, 8 см

2. Двое рабочих совместно могут выполнить заданную работу за 12 дней. Если первый рабочий сделает половину работы, а затем второй – вторую половину, то вся работа будет закончена за 25 дней нужно каждому из рабочих в отдельности для выполнения работы?

Решение: пусть для выполнения всей работы первому рабочему потребуется х дней, а второму у дней, тогда за 1 день первый выполняет 1/х часть, а второй 1/у часть всей работы. Работая совместно, всю работу они выполняют за 12 дней.

Таким образом 12(1/х+1/у)=1.

Пусть теперь работа выполняется рабочими поочередно. Тогда для выполнения половины всей работы первому потребуется 1/2:1/х=х/2 дней, а второму 1/2: 1/у=у/2 дней.

,

,

,

,

,

Одному рабочему для выполнения всей работы требуется 20 дней, а другому 30 дней.

Ответ: 20 дней, 30 дней

Решаем по учебнику: №455, №457 (15 мин)

IV. Итог урока.

Домашнее задание: №456, №458, №460 (2 мин)

Решение задач с помощью систем линейных уравнений

Алгоритм решения задачи с помощью системы линейных уравнений

1. Обозначить неизвестные величины переменными («от смысла к буквам»).
2. По условию задачи записать уравнения, связывающие обозначенные переменные.
3. Решить полученную систему уравнений.
4. Истолковать результат в соответствии с условием задачи («от букв к смыслу»).

Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.

«От смысла к буквам»:

Пусть x и y — задуманные числа.

Уравнения по условию задачи::

Решение системы уравнений:

«От букв к смыслу»:

Задуманы числа 37 и 27.

Примеры

Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.

Найдите стороны прямоугольника.

Пусть a и b — длина и ширина прямоугольника.

$$ <\left\< \begin P = 2(a+b) = 48 \\ a = 3b \end \right.> \Rightarrow <\left\< \begin a+b = 24 \\ a = 3b \end \right.> \Rightarrow <\left\< \begin 3b+b = 24 \\ a = 3b \end \right.> \Rightarrow <\left\< \begin 4b = 24 \\ a = 3b \end \right.> \Rightarrow <\left\< \begin a = 18 \\ b = 6 \end \right.> $$

Ответ: длина прямоугольника 18 см, ширина 6 см.

Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?

Пусть x — ежедневное количество строк для 1-го программиста, y- для 2-го.

$$ <\left\< \begin 70x+100y = 100500 |:10 \\ 30x-30y = 5550 |:30 \end \right.> (-) \Rightarrow <\left\< \begin 7x+10y = 10050 \\ x-y=185 | \times 10 \end \right.>$$

$$ \Rightarrow (+) <\left\< \begin 7x+10y = 10050 \\ 10x-10y = 1850 \end \right.> \Rightarrow <\left\< \begin 17x = 11900 \\ y = x-185 \end \right.> \Rightarrow <\left\< \begin x = 700 \\ y = 515 \end \right.> $$

Ответ: 700 строк и 515 строк

Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?

Пусть x — цена за 1 кг конфет, y — за 1 кг печенья.

$$ <\left\< \begin 2x+3y = 1540 \\ 2y-x = 210 | \times 2 \end \right.> \Rightarrow (+) <\left\< \begin 2x+3y = 1540 \\ -2x+4y = 420 \end \right.> \Rightarrow <\left\< \begin 7y = 1960 \\ x = 2y-210 \end \right.> \Rightarrow <\left\< \begin x = 350 \\ y = 280 \end \right.> $$

Ответ: 1 кг конфет — 350 руб. и 1 кг печенья — 280 руб.

Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.

Пусть v — скорость катера (км/ч), u — скорость течения (км/ч).

$$ \Rightarrow <\left\< \begin 5v-u = 73 \\ v+7u = 29 \end \right.> \Rightarrow <\left\< \begin 5(29-7u)-u = 73 \\ v = 29-7u \end \right.> \Rightarrow <\left\< \begin 145-35u-u = 73 \\ v = 29-7u \end \right.> \Rightarrow$$

Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч

Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.

Пусть x – первоначальная цена карандаша, y — тетрадки.

$$ <\left\< \begin 5x+3y = 170 \\ 3\cdot0,8x+5\cdot1,3y = 284 \end \right.> \Rightarrow <\left\< \begin 5x+3y = 170 |\times \frac<2,4> <5>\\ 2,4x+6,5y = 284 \end \right.> \Rightarrow (-) <\left\< \begin 2,4x+1,44y = 81,6 \\ 2,4x+6,5y = 284 \end \right.> $$

Ответ: карандаш сначала стоил 10 руб., тетрадка — 40 руб.

Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.

Пусть v – обычная скорость велосипедиста (км/ч), t — обычное время (ч).

Расстояние между А и В неизменно, и по условию равно:

Ответ: обычная скорость 12 км/ч, время 5 ч

Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.

Пусть x — объём первой бочки (л), y – объём второй (л).

Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:

Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:

$$ <\left\< \begin x+ \frac<1> <2>y = 44 | \times 2 \\ \frac<1> <6>x+y = 44 \end \right.> \Rightarrow (-) <\left\< \begin 2x+y = 88 \\ \frac<1> <6>x+y = 44 \end \right.> \Rightarrow (+) <\left\< \begin 1\frac<5> <6>x = 44 \\ y = 88-2x \end \right.> \Rightarrow $$

Ответ: первая бочка 24 л, вторая – 40 л

Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?

Пусть s — расстояние между домом и школой, v — скорость автобуса, u — скорость школьника, t — искомое время, потраченное на дорогу туда и обратно пешком.

По условию задачи:

Из второго уравнения $ \frac = \frac<0,5> <2>= 0,25 $. Подставляем в первое уравнение:

И тогда искомое время:

$$ t = \frac<2s> = 2\cdot1,25 = 2,5 (ч) $$

Решение задач с помощью систем линейных уравнений

Примеры оформления и образцы решения задач с помощью систем линейных уравнений.

Просмотр содержимого документа
«Решение задач с помощью систем линейных уравнений»

Системы двух линейных уравнений с двумя переменными как математические модели реальных жизненных ситуаций

Множество задач можно решить путем составления систем двух линейных уравнений .

1) построение математической модели ( обозначить через x и y неизвестные величины );

2) составление системы двух уравнений и ее решения; 3) нахождение ответа к задаче.

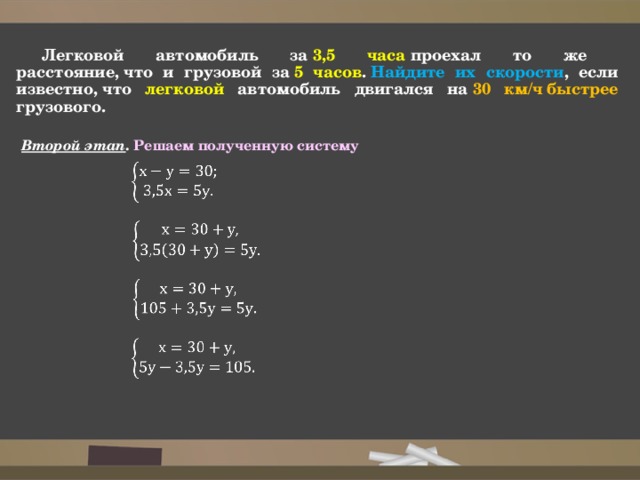
Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов . Найдите их скорости , если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Первый этап . Составляем математическую модель задачи

?, на 30 км/ч быстрее

Обозначим скорость легкового автомобиля – х км/ч, а скорость грузового автомобиля — у км/ч. Оба автомобиля проехали одинаковое расстояние ( S=Vt) .

Составим и решим систему уравнений:

Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов . Найдите их скорости , если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Второй этап . Решаем полученную систему

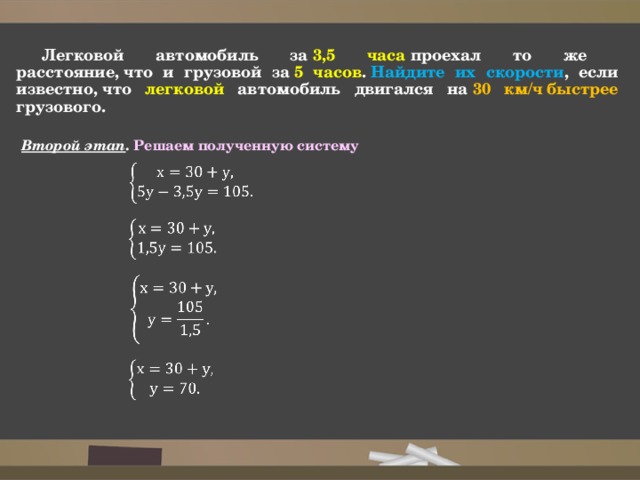
Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов . Найдите их скорости , если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Второй этап . Решаем полученную систему

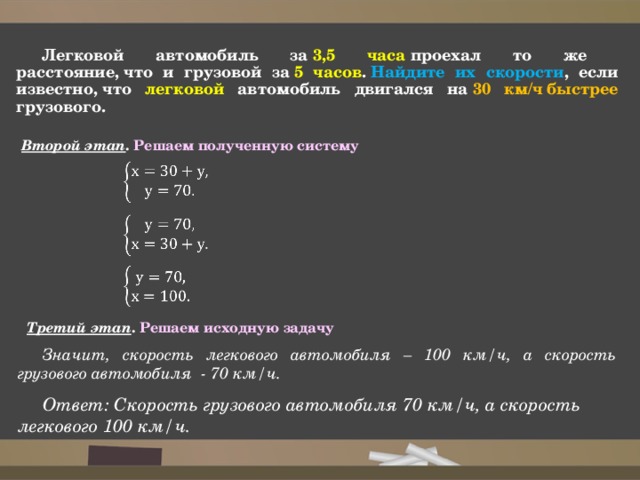
Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов . Найдите их скорости , если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Второй этап . Решаем полученную систему

Значит, скорость легкового автомобиля – 100 км/ч, а скорость грузового автомобиля — 70 км/ч.

Ответ: Скорость грузового автомобиля 70 км/ч, а скорость легкового 100 км/ч.

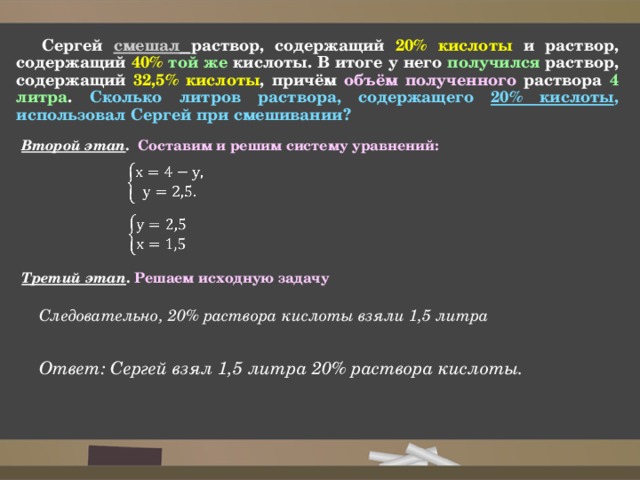
Сергей смешал раствор, содержащий 20% кислоты и раствор, содержащий 40% той же кислоты. В итоге у него получился раствор, содержащий 32,5% кислоты , причём объём полученного раствора 4 литра . Сколько литров раствора, содержащего 20% кислоты, использовал Сергей при смешивании?

Первый этап . Составляем математическую модель задачи

Итого (смесь 1 и 2 растворов)

Объем раствора, л

Обозначим объем 1 раствора – х, а второго — у. Тогда объем кислоты в первом растворе 0,2х л, а во втором – 0,4у л. Объем кислоты в новом растворе 4  0,325=1,3 л.

Сергей смешал раствор, содержащий 20% кислоты и раствор, содержащий 40% той же кислоты. В итоге у него получился раствор, содержащий 32,5% кислоты , причём объём полученного раствора 4 литра . Сколько литров раствора, содержащего 20% кислоты, использовал Сергей при смешивании?

Второй этап . Составим и решим систему уравнений:

Сергей смешал раствор, содержащий 20% кислоты и раствор, содержащий 40% той же кислоты. В итоге у него получился раствор, содержащий 32,5% кислоты , причём объём полученного раствора 4 литра . Сколько литров раствора, содержащего 20% кислоты , использовал Сергей при смешивании?

Второй этап . Составим и решим систему уравнений:

Следовательно, 20% раствора кислоты взяли 1,5 литра

Ответ: Сергей взял 1,5 литра 20% раствора кислоты.

Иван случайно смешал молоко жирностью 2,5% и молоко жирностью 6% . В итоге у него получилось 5 литров молока жирностью 4,6% . Сколько литров молока жирностью 2,5% было у Ивана до смешивания?

Первый этап . Составляем математическую модель задачи