С 34 простейшие тригонометрические уравнения и неравенства

Простейшие тригонометрические уравнения (задание 5) и неравенства

\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad \mathrm\,x=b,\quad \mathrm\,x=b\) , которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb\) .

Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\) ).

Рассмотрим несколько примеров:

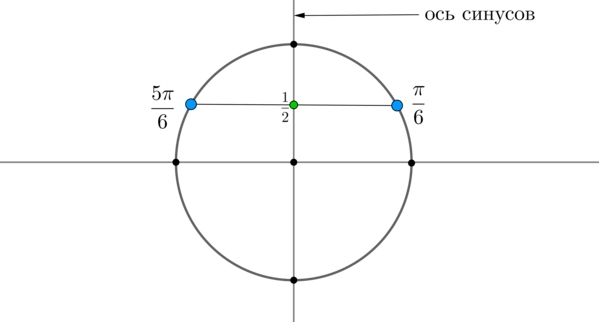
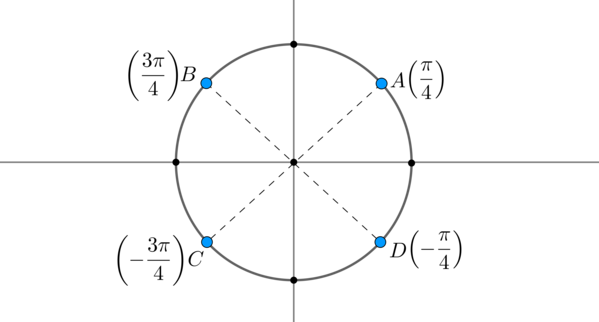
Пример 1. Решить уравнение \(\sin x=\dfrac12\) .

Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\) , где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).

Таким образом, решением являются \(x_1=\dfrac<\pi>6+2\pi n,\ x_2=\dfrac<5\pi>6+2\pi n, \ n\in \mathbb\) .

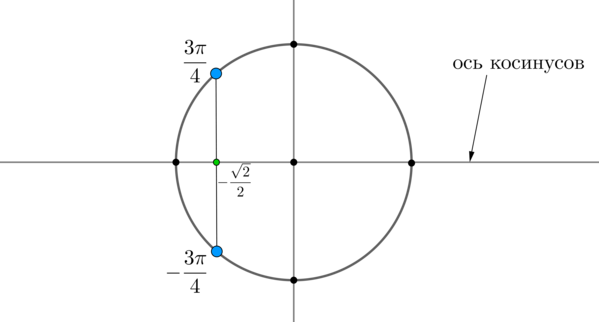
Пример 2. Решить уравнение \(\cos x=-\dfrac<\sqrt2><2>\) .

Найдем на оси косинусов точку \(-\dfrac<\sqrt2><2>\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac<\sqrt2><2>\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<3\pi>4\) и \(-\dfrac<3\pi>4\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число.

Таким образом, решением являются \(x_1=\dfrac<3\pi>4+2\pi n,\ x_2=-\dfrac<3\pi>4+2\pi n, \ n\in \mathbb\) .

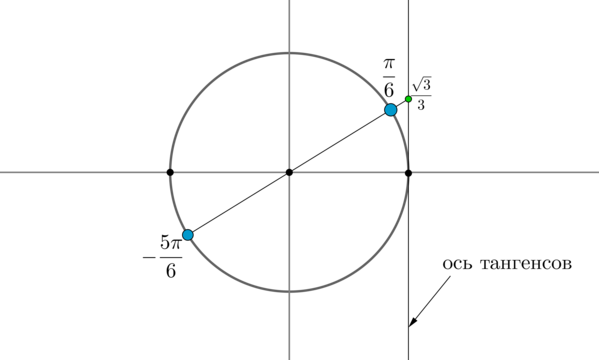
Пример 3. Решить уравнение \(\mathrm\,x=\dfrac<\sqrt3>3\) .

Найдем на оси тангенсов точку \(\dfrac<\sqrt3>3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac<\sqrt3>3\) .Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

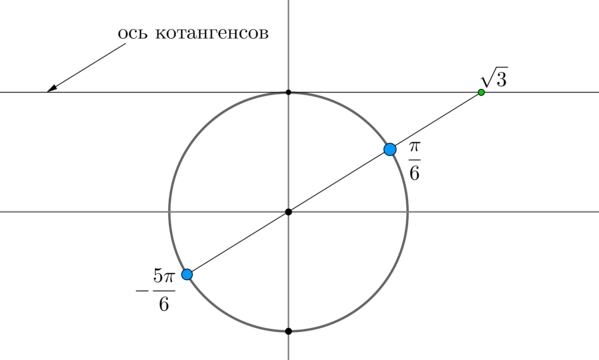
Пример 4. Решить уравнение \(\mathrm\,x=\sqrt3\) .

Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin \hline \text <Уравнение>& \text <Ограничения>& \text<Решение>\\ \hline &&\\ \sin x=a & -1\leq a\leq 1 & \left[ \begin \begin &x=\arcsin a+2\pi n\\ &x=\pi -\arcsin a+2\pi n \end \end \right. \ \ , \ n\in \mathbb\\&&\\ \hline &&\\ \cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\, x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\,x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline \end\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb\) .

\(\blacktriangleright\) Любые уравнения вида \(\mathrm\,\big(f(x)\big)=a\) , (где \(\mathrm\) — одна из функций \(\sin, \ \cos, \ \mathrm,\ \mathrm\) , а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\) .

Пример 5. Решить уравнение \(\sin<(\pi x+\dfrac<\pi>3)>=1\) .

Сделав замену \(t=\pi x+\dfrac<\pi>3\) , мы сведем уравнение к виду \(\sin t=1\) . Решением данного уравнения являются \(t=\dfrac<\pi>2+2\pi n, n\in\mathbb\) .

Теперь сделаем обратную замену и получим: \(\pi x+\dfrac<\pi>3=\dfrac<\pi>2+2\pi n\) , откуда \(x=\dfrac16+2n,\ n\in\mathbb\) .

Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac<2\pi>n,\ n\in\mathbb\) , где \(\alpha\) — один из этих углов.

Рассмотрим данную ситуацию на примере:

Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac<\pi>4+2\pi n, \ x_2=\pm \dfrac<3\pi>4+2\pi n, \ n\in\mathbb\) . Отметим эти точки на окружности:

Заметим, что длины дуг \(\buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over\) равны \(\dfrac<\pi>2\) , то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac<\pi>4+\dfrac<\pi>2n, \ n\in\mathbb\) .

где \(\lor\) — один из знаков \(\leq,\ ,\ \geq\) .

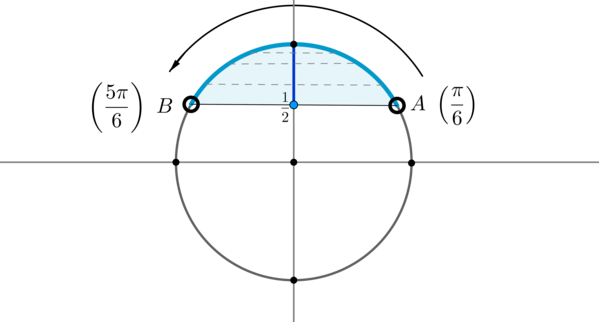
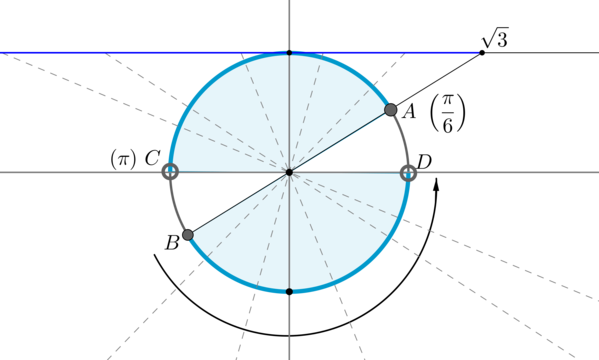
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\) .

Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, синус которых больше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>6\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>6\) , но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>6\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>6;\dfrac<5\pi>6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac<\pi>6+2\pi n;\dfrac<5\pi>6+2\pi n\right), n\in\mathbb\) , т.к. у синуса период \(2\pi\) .

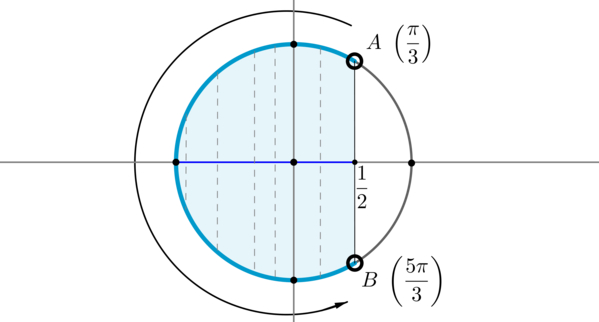
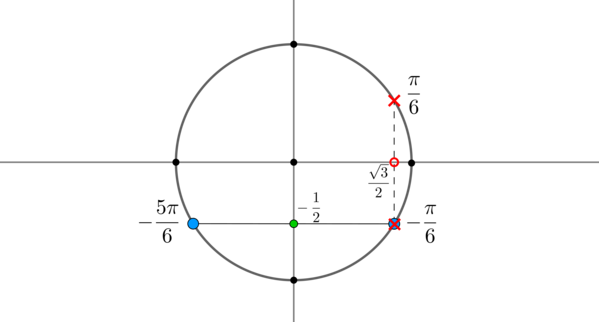
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x .

Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, косинус которых меньше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>3\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>3\) , но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>3\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>3;\dfrac<5\pi>3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac<5\pi>3+2\pi n;-\dfrac<\pi>3+2\pi n\right), n\in\mathbb\) , т.к. у косинуса период \(2\pi\) .

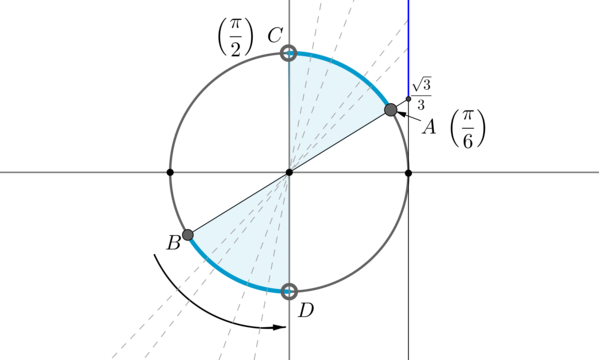
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm\, x \geq \dfrac<\sqrt<3>>3\) .

Для начала отметим на окружности корни уравнения \(\mathrm\, x = \dfrac<\sqrt<3>>3\) . Это точки \(A\) и \(B\) . Все точки, тангенс которых больше или равен \(\dfrac<\sqrt<3>>3\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac<\pi>2\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\dfrac<\pi>2\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\dfrac<\pi>2\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\dfrac<\pi>2+\pi n\Big), n\in\mathbb\) , т.к. у тангенса период \(\pi\) .

Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm\, x \leq \sqrt<3>\) .

Для начала отметим на окружности корни уравнения \(\mathrm\, x = \sqrt<3>\) . Это точки \(A\) и \(B\) . Все точки, котангенс которых меньше или равен \(\sqrt<3>\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\pi\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\pi\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\pi+\pi n\Big), n\in\mathbb\) , т.к. период котангенса \(\pi\) .

Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.

Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\) , если \(\cos x\ne \dfrac<\sqrt3>2\) .

В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.

Решением первого уравнения являются \(x_1=-\dfrac<\pi>6+2\pi n,\ x_2=-\dfrac<5\pi>6+2\pi n,\ n\in \mathbb\) , решением второго являются \(x\ne \pm \dfrac<\pi>6+2\pi n,\ n\in\mathbb\) . Отметим эти точки на окружности:

Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac<\pi>6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac<5\pi>6+2\pi n, n\in \mathbb\) .

Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin &\sin<(\alpha+\pi n)>=\begin \sin \alpha, \text <при >n — \text< четном>\\ -\sin \alpha, \text <при >n — \text < нечетном>\end\\ &\cos<(\alpha+\pi n)>=\begin \cos \alpha, \text <при >n — \text< четном>\\ -\cos \alpha, \text <при >n — \text <нечетном>\end\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\sin<\left(\alpha+\dfrac<\pi>2\right)>=\cos\alpha\\ &\cos<\left(\alpha+\dfrac<\pi>2\right)>=-\sin \alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha \end\]

Пример 12. Решить систему \(\begin \cos x=\dfrac12\\ \sin x+\cos x>0\end\)

Решением уравнения являются \(x_1=\dfrac<\pi>3+2\pi n,\ x_2=-\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) . Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:

\(\sin x_1+\cos x_1=\dfrac<\sqrt3>2+\dfrac12>0\) , следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac<\sqrt3>2+\dfrac12 , следовательно, корень \(x_2\) нам не подходит.

Таким образом, решением системы являются только \(x=\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) .

Алгебраический способ.

Пример 13. Найти корни уравнения \(\sin x=\dfrac<\sqrt2>2\) , принадлежащие отрезку \([0;\pi]\) .

Решением уравнения являются \(x_1=\dfrac<\pi>4+2\pi n, \ x_2=\dfrac<3\pi>4 +2\pi n, \ n\in\mathbb\) . Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq x_2\leq\pi\) :

\(0\leq \dfrac<\pi>4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\) . Таким образом, единственное целое значение \(n\) , удовлетворяющее этому неравенству, это \(n=0\) . При \(n=0\) \(x_1=\dfrac<\pi>4\) — входит в отрезок \([0;\pi]\) .

Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac<3\pi>4\) .

Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:

Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\) .

Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\) . Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\) , то есть нечетное число.

Пример: Решить уравнение \(3x+5y=2\) . Т.к. \(НОД(3,5)=1\) , то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\) :

Число \(\dfrac<2-2y>3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\) : \(0\) , \(1\) или \(2\) .
Если \(y\) при делении на \(3\) имеет остаток \(0\) , то оно записывается как \(y=3p+0\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2\cdot 3p>3=\dfrac23-2p\ne \text<целому числу>\]

Если \(y\) при делении на \(3\) имеет остаток \(1\) , то оно записывается как \(y=3p+1\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2(3p+1)>3=-2p=\text<целому числу>\]

Значит, этот случай нам подходит. Тогда \(y=3p+1\) , а \(x=\dfrac<2-2y>3-y=-5p-1\) .

Ответ: \((-5p-1; 3p+1), p\in\mathbb\) .

Перейдем к примеру:

Пример 14. Решить систему \[\begin \sin \dfrac x3=\dfrac<\sqrt3>2\\[3pt] \cos \dfrac x2=1 \end\]

Решим первое уравнение системы:

\[\left[ \begin \begin &\dfrac x3=\dfrac<\pi>3+2\pi n\\[3pt] &\dfrac x3=\dfrac<2\pi>3 +2\pi m \end \end \right.\quad n,m\in\mathbb \quad \Leftrightarrow \quad \left[ \begin \begin &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end \end \right.\quad n,m\in\mathbb\]

Решим второе уравнение системы:

\[\dfrac x2=2\pi k, k\in\mathbb \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb\]

Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\) , при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\) :

\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]

Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\) , то данное уравнение не имеет решений в целых числах.

Найдем целые \(m\) и \(k\) , при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\) :

\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]

Данное уравнение имеет решение в целых числах. Выразим \(k=\frac<3m+1>2=m+\frac2\) .

Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\) .
Если \(m=2p+0\) , то \(\frac2=\frac<2p+1>2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\) , то \(\frac2=\frac<2p+1+1>2=p+1= \) целому числу.

Значит, \(m=2p+1\) , тогда \(k=3p+2\) , \(p\in\mathbb\) .

Подставим либо \(m\) , либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb\) .

ГДЗ Алгебра Самостоятельные работы за 10 класс Александрова Базовый уровень Мнемозина (к учебнику Мордкович)

Алгебра в 10 классе имеет свои трудности, которые он должен преодолеть как можно скорее. Эти проблемы касаются не только правил, формул, но и умения мыслить и понимать задачи. А это умение, как известно, является одной из самых сложных способностей человека. Выполнение самостоятельной работы по алгебре ставит перед десятиклассником ряд личностно – значимых проблем, которые позволяют понять самому, как решать задачи. Это не просто подготовка к работе на уроке по шаблону, но и самостоятельное создание ситуации успеха, которая должна стать нормой для каждого ученика. Только в этом случае, любой десятиклассник сможет найти возможность проявить свои способности, почувствовать, что он чего – то может достичь самостоятельно. Проверить правильность выполненных решений можно с помощью ГДЗ по алгебре и начала математического анализа Александрова Л.А., которое полностью соответствует всем требованиям школьной программы основного среднего образования и федеральному государственному общеобразовательному стандарту.

Сформировать умения применять свои знания на практике в различных ситуациях и разных предметных областях является одной из главных задач обучения. Освоение знаний – это только половина дела. Главное это иметь большое желание учиться, быть любознательным, а так же уметь добывать эти знания, пользоваться ими в определенной ситуации, такого требования общеобразовательного стандарта.

Одной из основных причин неспособность школьника применять математические знания в практической работе является отсутствие или недостаток знаний об общих закономерностях, умение осуществлять выбор способа решения в конкретной ситуации, а так же и опыта применения математики для решения задач в смежных предметах. Овладеть школьником методов решения задач повышает его уровень математического развития. Математический язык относится к числу наиболее распространенных языков. Он широко используется в литературе, в печати, в научно – технических и практических публикациях. Благодаря этому и язык математики получил широкое применение в других научных дисциплинах. Язык математики имеет свои законы развития, что объясняется её природой. В языке математики можно выделить две основные составляющие: – это естественный язык (его ещё называют языком логики), на котором принято выражать мысли, и символы, которыми изображаются эти мысли. Именно при обучении алгебры в школе ставится задача овладеть символьным языком алгебры, это и позволит ученику глубже разобраться в математических моделях, что в свою очередь позволит в дальнейшем более полно использовать математический аппарат в экономических расчетах. Для этого в качестве объектов исследования были выбраны некоторые элементы математического аппарата алгебры, такие как определители, матрица, вектор, операции, сложение и так далее. Необходимость изучения комплекс чисел в курсе алгебры и начала математического анализа обуславливается потребностью в математических моделях многих физических явлений. В настоящее время одним из основных направлений развития теории дифференциальных уравнений является её приложение к задачам механики сплошных сред. Это направление связано с созданием теории одномерных и двумерных уравнений математической физики, где на первый план выходят задачи о фазовых переходах. Для решения таких задач необходимо знание свойств интегральных представлений функции, имеющие множество точек разрыва.

ГДЗ по алгебре Самостоятельные работы за 10 класс Александрова Базовый уровень к учебнику Мордкович

Курс алгебры и начала математического анализа является основой для получения фундаментальных знаний в областях, непосредственно примыкающих к школьной программе и для продолжения образования в технических, экономических и гуманитарных в высших учебных заведениях. К тому же курс алгебры и начала математического анализа является завершающим этапом в школьном обучении математики. Этот курс имеет большую практическую значимость, что связано с формированием и развитием ряда умений и навыков. При изучении этой дисциплины у десятиклассника вырабатываются навыки работы с тестовыми заданиями. Ученик учится самостоятельно работать, наблюдать, обобщать, делать выводы, применять теоретические знания на практике. Умения и навыки формируются в процессе решения примеров и задач. Для этого отлично подойдет использование ГДЗ по алгебре и начала математического анализа 10 класс Александрова Л.А., который поможет глубже вникнуть в систему понятий, необходимых для решения задач, входящих в школьный курс элементарной математики. В нем отражены все темы учебника такие как:

• числовые функции,
• тригонометрические функции и уравнения,
• преобразование тригонометрических выражений,
• производная.

Решебник является можно сказать, что по сути своей он выполняет функции репетитора по алгебре. Он содержит в себе не только решения простых примеров и задач, но и более сложных. Пользоваться онлайн – решебником можно в любое, удобное для школьника, время и в любом месте, где имеется выход в Интернет, хоть с компьютера, хоть с любого электронного устройства. С его помощью каждый ученик сможет:

• получить полное качественное выполнение домашнего задания,
• провести подготовку, как к самостоятельной работе, так и подготовку к следующему уроку,
• устранить имеющиеся пробелы в знании той или иной темы,
• закрепить знания.

Решебник поможет и родителям проверить, насколько их ребенок знает алгебру.

Его может использовать и учитель математики для проверки домашнего задания, подготовке к самостоятельной работе, а так же как справочное пособие.

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение тригонометрических неравенств.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое неравенство. Программа для решения тригонометрического неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое неравенство
Решить неравенство

Немного теории.

Тригонометрические неравенства

Неравенства вида \( \sin x > a \) и \( \sin x

Пусть дано простейшее неравенство \( \sin x > a \).
1) При \(-1 1 \) решением неравенства является любое действительное число: \( x \in \mathbb \)
3) При \(а = 1 \) решением неравенства является любое действительное число, отличное от \( \frac<\pi> <2>+ 2\pi k, \; k \in \mathbb \)
4) При \(а \leqslant -1 \) неравенство не имеет решений.

Неравенства вида \( \cos x > a \) и \( \cos x

Пусть дано простейшее неравенство \( \cos x > a \).
1) При \(-1 1\) решением неравенства является любое действительное число: \( x \in \mathbb \)
3) При \(a \leqslant -1\) неравенство не имеет решений.
4) При \(a = 1\) решением неравенства является любое действительное число, отличное от \( 2\pi k, \; k \in \mathbb \)

Неравенства вида \( tg \;x > a \) и \( tg \;x

Пусть дано простейшее неравенство \( tg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb \) решение неравенства будет таким:
$$ x \in \left(arctg \;a + \pi k; \;\; \frac<\pi> <2>+ \pi k \right), \; k \in \mathbb $$

Пусть дано простейшее неравенство \( tg \;x

Неравенства вида \( ctg \;x > a \) и \( ctg \;x

Пусть дано простейшее неравенство \( ctg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb \) решение неравенства будет таким:
$$ x \in ( \pi k; \;\; arcctg \;a + \pi k ), \; k \in \mathbb $$

Пусть дано простейшее неравенство \( ctg \;x

Решение тригонометрических неравенств

ПРИМЕР 1. Решим неравенство \( \sin x > \frac<1> <2>\).
Так как \( -1 \frac<1> <2>\).
Так как \( -1 1 \).
Очевидно, что решение неравенства будет таким:
$$ x \in \left(\frac<\pi> <4>+ \pi k; \;\; \frac<\pi> <2>+ \pi k\right), \; k \in \mathbb $$

ПРИМЕР 6. Решим неравенство \( tg \;x \frac<\sqrt<3>> <3>\).
Очевидно, что решение неравенства будет таким:
$$ x \in \left( \pi k; \;\; \frac<\pi> <3>+ \pi k \right), \; k \in \mathbb $$

ПРИМЕР 8. Решим неравенство \( ctg \;x