С помощью изоклин начертить решения данных уравнений

Метод изоклин для дифференциальных уравнений 1-го порядка

Дифференциальное уравнение первого порядка

Если в каждой точке области задано значение некоторой величины, то говорят, что в области задано поле этой величины. Таким образом, дифференциальное уравнение (1) определяет поле направлений.

Тройка чисел определяет направление прямой, проходящей через точку . Совокупность отрезков этих прямых дает геометрическую картину поля направлений.

Задача интегрирования дифференциального уравнения (1) может быть теперь истолкована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.

Задача построения интегральной кривой часто решается введением изоклин . Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и тоже направление. Семейство изоклин дифференциального уравнения (1) определяется уравнением

где — параметр. Придавая параметру близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения (1).

Замечание 1. Нулевая изоклина дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых.

Для большей точности построения интегральных кривых находят также геометрическое место точек перегиба. Для этого находят в силу уравнения (1):

и приравнивают ее нулю. Линия, определяемая уравнением

и есть возможное геометрическое место точек перегиба.

Пример 1. С помощью изоклин построить приближенно интегральные кривые дифференциального уравнения .

Решение. Для получения уравнения изоклин положим , тогда или .

Изоклинами являются параллельные прямые. При получим изоклину . Эта прямая делит плоскость на две части, в каждой из которых производная имеет один и тот же знак (рис. 6).

Интегральные кривые, пересекая прямую , переходят из области убывания функции в область возрастания, и наоборот, а значит на этой прямой находятся точки экстремума интегральных кривых, именно точки минимума.

Возьмем еще две изоклины: и .

Касательные, проведенные к интегральным кривым в точках пересечения с изоклинами и , образуют с осью углы в и соответственно. Найдем далее вторую производную .

Прямая , на которой , является изоклиной, получаемой при , и в то же время интегральной линией, в чем можно убедиться подстановкой в уравнение. Так как правая часть данного уравнения удовлетворяет условиям теоремы существования и единственности во всей плоскости , то остальные интегральные кривые не пересекают эту изоклину. Изоклина , на которой находятся точки минимума интегральных кривых, расположена над изоклиной , а поэтому интегральные кривые, проходящие ниже изоклины , не имеют точек экстремума.

Прямая делит плоскость на две части, в одной из которых (расположенной над прямой) 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFEIdthoX7wMRGRsJ7q5I0AAAEISURBVCjPY2CgDLDM4HqMU5LtGccrnJLsE5gC0IQYrQSgLNYDfAlokitrgqEsPwfLDWiumMZg6QBhJjG0g2l3B5gkzwMGuQMQ5jEGLTDNrG4As0iRQSiQgfuSAYPZBgaoFq4iQwhDDij5kEFoTSBDEJJdRYlgeh9Q8jVDBmsAywtkl5SCZe0UGJgeM5isa2BDCR3uVpC968CSDH0O7A8xJeXAxjKoCrAqIBvbmsgIpCSBkhMZGN8y+DUgWwkJKnagPwsYGIMY6gyQHAv1CjCW7AwYGC1r58GCmIFZCa4utWMakNxoPReuERF8DCzJQDZnIBv2eBYERciBlQk445lH6TKe9COIWwoABhM22oebiGoAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, а значит интегральные кривые обращены вогнутостью вверх, а в другой и, значит, интегральные кривые обращены вогнутостью вниз. Интегральные кривые не пересекают прямой , значит, она не является геометрическим местом точек перегиба. Интегральные кривые данного уравнения не имеют точек перегиба.

Проведенное исследование позволяет нам приближенно построить семейство интегральных кривых уравнения (рис.6).

Пример 2. Методом изоклин построить приближенно интегральные кривые дифференциального уравнения .

Решение. Полагая , где , получаем уравнение изоклин , причем . При получим , откуда

Интегральные кривые в точках пересечения с этими изоклинами имеют горизонтальные касательные.

Определим, имеют ли интегральные кривые на изоклинах экстремум. Для этого найдем вторую производную:

Если четное, то 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFEIdthoX7wMRGRsJ7q5I0AAAEISURBVCjPY2CgDLDM4HqMU5LtGccrnJLsE5gC0IQYrQSgLNYDfAlokitrgqEsPwfLDWiumMZg6QBhJjG0g2l3B5gkzwMGuQMQ5jEGLTDNrG4As0iRQSiQgfuSAYPZBgaoFq4iQwhDDij5kEFoTSBDEJJdRYlgeh9Q8jVDBmsAywtkl5SCZe0UGJgeM5isa2BDCR3uVpC968CSDH0O7A8xJeXAxjKoCrAqIBvbmsgIpCSBkhMZGN8y+DUgWwkJKnagPwsYGIMY6gyQHAv1CjCW7AwYGC1r58GCmIFZCa4utWMakNxoPReuERF8DCzJQDZnIBv2eBYERciBlQk445lH6TKe9COIWwoABhM22oebiGoAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, и, значит, в точках пересечения с изоклинами , интегральные кривые имеют минимум; если же нечетное, то и интегральные кривые в точках пересечения с изоклинами имеют максимум. Находим изоклины:

Изоклинами являются параллельные прямыми с угловым коэффициентом, равным –1 , т. е. изоклины пересекают ось под углом . Легко убедиться в том, что изоклины , являются интегральными кривыми данного дифференциального уравнения (для этого достаточно подставить функции в уравнение ).

Во всех точках плоскости правая часть данного уравнения, т.е. функция , удовлетворяет всем условиям теоремы существования и единственности, а поэтому интегральные кривые не пересекаются, и, следовательно, не пересекают изоклины . Производная обращается в ноль при , т.е. на изоклинах (6), и при , т. е. на изоклинах (6) и (7). При переходе (слева направо) через изоклины (7) меняет знак с плюса на минус. Например, если рассмотреть полосу, заключенную между изоклинами и , то на изоклине производная , причем под изоклиной 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFEIdthoX7wMRGRsJ7q5I0AAAEISURBVCjPY2CgDLDM4HqMU5LtGccrnJLsE5gC0IQYrQSgLNYDfAlokitrgqEsPwfLDWiumMZg6QBhJjG0g2l3B5gkzwMGuQMQ5jEGLTDNrG4As0iRQSiQgfuSAYPZBgaoFq4iQwhDDij5kEFoTSBDEJJdRYlgeh9Q8jVDBmsAywtkl5SCZe0UGJgeM5isa2BDCR3uVpC968CSDH0O7A8xJeXAxjKoCrAqIBvbmsgIpCSBkhMZGN8y+DUgWwkJKnagPwsYGIMY6gyQHAv1CjCW7AwYGC1r58GCmIFZCa4utWMakNxoPReuERF8DCzJQDZnIBv2eBYERciBlQk445lH6TKe9COIWwoABhM22oebiGoAAAAASUVORK5CYII=» style=»vertical-align: middle;» />. Значит, интегральные кривые обращены вогнутостью вверх, а над изоклиной , значит, интегральные кривые обращены вогнутостью вниз. Таким образом, изоклины (7) являются геометрическим местом точек перегиба интегральных кривых. Полученные данные позволяют приближенно построить семейство интегральных кривых данного уравнения. Для более точного построения следует нанести еще несколько изоклин (рис. 7).

Пример 3. Методом изоклин построить интегральные кривые уравнения .

Решение. Положим . Тогда уравнение изоклин будет

Изоклинами являются параболы с вертикальной осью симметрии . Среди изоклин нет интегральных кривых. В самом деле, подставляя в данное уравнение и , будем иметь , или . Но это равенство ни при каком значении не может выполняться тождественно относительно .

Пусть , тогда в точках пересечения с изоклиной интегральные кривые будут иметь горизонтальные касательные. Изоклина разбивает плоскость на две части: в одной из них (решения убывают), а в другой 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADQAAAAXBAMAAAC2bnFAAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAncEhYUEQgTHg8NGxUXFruPrBAAAA30lEQVQoz2NgIB8wr8MpxfIFpxTjAnSRDhiDUwBNplNwBpRlb4Bh9y2okBOYTIQrYPzAwAU1SARMsp4JgEpxb2BgmsDAJtTAcDcBao4QVI5fgYHpAwNT4wSGOXA7pB3gUt8Y3LknMH9H2F8NlusHSn1lCO5/wPIV4TY2sBw/WIqh3oDnA7JUAdxABm0GLgU0TQycQBcCA+gjg30BujOA/uIH+msOgzzMO3DHM39hiAcyvYTWQ2VYD8HUMHiKTwGantCwEMpPbEDYCQoFrgl8n3FElX1BlwMOKXadE6QnGABHNTFBqOdYeAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> (решения возрастают). И так как эта изоклина не является интегральной кривой, то на ней находятся точки экстремума интегральных кривых, именно на той части параболы , где — точки минимума, а на другой части этой параболы, где 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcChQSFZMdCB6RCQsVNol/AAAACdSURBVBjTY2AgCbDjEBexE8Aqzrl2HbJEZQCcKaiHLMGiDJdhBEvs0dymDJVxQJbgVpForkqAyBg5IEnwOPC+ngeRYGA1SkRIsDFIKWyHGc5qlQCXYGSImwB3AOsJhAQDY54DXBzZKGaDewISEGezGzkIIiTqtFcxZEIcpQvTKtAHVMBxwsPoAKoHWd69ewe0t5AhEMwtRgoSQUEGAFJBHb3FaZBuAAAAAElFTkSuQmCC» /> — точки максимума. Интегральная кривая, проходящая через точку , т.е. через вершину параболы , в этой точке не имеет экстремума. В точках изоклин и касательные к интегральным кривым имеют угловые коэффициенты, соответственно равные 1 и –1.

Для исследования направления вогнутости интегральных кривых найдем вторую производную:

Она обращается в ноль только в точках, лежащих на параболе . В точках плоскости , координаты которых удовлетворяют условию , интегральные кривые вогнуты вниз , а в точках, где x^2″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADkAAAAYCAMAAAB3NqUkAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEXRSTlMA0KEwwGKBBhD6IUGwkHFR4HWSoZwAAAD0SURBVDjLvVTZrsQgCBVBAnVp//9rB6fJ1FJz78SH4alBD/YsGsLvSpjzGrBsu/IKMukWmq4gsUjYFRepRlgE4uqRQtt8gdM/wCghydwv+AsrUJlPnlJp7z/fRiz7oTsVxFjQPqziu1eQuz10jIOTw1Y2E0GIhl6uoXSkRuc4xEsItMWsKWsZkZvo2X+kBaJ8NplyFp4sLk/Gs+pD6kxx3Hijc1bRWT8d8T7L0+kgevadQonsghiddqdE5k4baQofzhXSrWgOSD6GkY6LZk+Cd7MBpQaVHnnNAhfNOkuQ2CzxGoJOPfmizF2c6PbN80AEOfyyXgEyBo3d+df6AAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, они вогнуты вверх 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADgAAAAXBAMAAACsUpHOAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcFEIdthoX7wMRGRsJ7q5I0AAAEISURBVCjPY2CgDLDM4HqMU5LtGccrnJLsE5gC0IQYrQSgLNYDfAlokitrgqEsPwfLDWiumMZg6QBhJjG0g2l3B5gkzwMGuQMQ5jEGLTDNrG4As0iRQSiQgfuSAYPZBgaoFq4iQwhDDij5kEFoTSBDEJJdRYlgeh9Q8jVDBmsAywtkl5SCZe0UGJgeM5isa2BDCR3uVpC968CSDH0O7A8xJeXAxjKoCrAqIBvbmsgIpCSBkhMZGN8y+DUgWwkJKnagPwsYGIMY6gyQHAv1CjCW7AwYGC1r58GCmIFZCa4utWMakNxoPReuERF8DCzJQDZnIBv2eBYERciBlQk445lH6TKe9COIWwoABhM22oebiGoAAAAASUVORK5CYII=» style=»vertical-align: middle;» />. Точки пересечения интегральных кривых с параболой являются точками перегиба этих кривых. Итак, парабола есть геометрическое место точек перегиба интегральных кривых.

Правая часть исходного уравнения во всех точках плоскости удовлетворяет условиям теоремы существования и единственности, поэтому через каждую точку плоскости проходит единственная интегральная кривая уравнения.

Используя полученные сведения, строим приближенно семейство интегральных кривых данного уравнения (рис. 8).

Замечание 2. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.

Рассмотрим уравнение . Семейство изоклин определяется уравнением . Это семейство прямых, проходящих через начало координат, так что в начале координат пересекаются изоклины, отвечающие различным наклонам касательных к интегральным кривым. Нетрудно убедиться, что общее решение данного уравнения имеет вид и точка является особой точкой дифференциального уравнения. Здесь изоклины являются интегральными кривыми уравнения (рис. 9).

Пример 4. Методом изоклин построить интегральные кривые уравнения .

Решение. Полагая , получаем уравнение семейства изоклин . Таким образом, изоклинами являются прямые, проходящие через начало координат .

При получим изоклину , при — изоклину , при — изоклину .

Рассматривая обратное уравнение найдем изоклину , во всех точках которой интегральные кривые имеют вертикальные касательные.

В точке пересекаются все изоклины данного уравнения (особая точка уравнения). С помощью полученных изоклин строим интегральные кривые (рис. 10).

И методы их решения. Метод изоклин (графическое решение)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Дифференциальные уравнения первого порядка.

Основные понятия

Дифференциальным уравнением(ДУ) называется уравнение, связывающее независимую переменную , искомую функцию и её производные или дифференциалы.

— — дифференциальное уравнение первого порядка, неявный вид.

— — уравнение, разрешённое относительно производной.

— — дифференциальная форма записи дифференциального уравнения первого порядка.

ДУ с одной независимой переменной называется обыкновенным.

ПорядкомДУ называется порядок наивысшей производной (или дифференциала), входящей в уравнение.

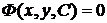
Всякая функция, удовлетворяющая ДУ, т.е. при подстановке в уравнение обращающая его в тождество, называется решением уравнения. Бесконечное множество решений уравнения называется общим решением ДУ. Общее решение имеет вид , где C – произвольная постоянная. Если решение задано в неявном виде, то оно обычно называется интегралом. Множество интегралов называется общим интегралом и имеет вид .

Каждому решению уравнения соответствует линия (график), называемая интегральной кривой этого уравнения.

Задача отыскания решения ДУ первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши.

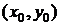
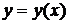
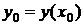
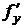
Теорема (существования и единственности задачи Коши). Если функция непрерывна в области, содержащей точку , то уравнение имеет решение такое, что . Если, кроме того, непрерывна и частная производная , то это решение – единственное.

Условие, при котором значение искомой функции равно при , называется начальным условием уравнения и записывается .

Решение ДУ, удовлетворяющее заданному начальному условию, называется частным решением.

а) 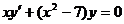– ДУ 1-го порядка в неявном виде.

б) – ДУ 1-го порядка в дифференциальной форме.

в) – ДУ 1-го порядка разрешенное относительно производной.

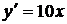
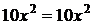
Пример 1.Выяснить, является ли функция решением уравнения ?

Решение. . Полученную производную подставим в уравнение. Тогда , . Получили верное тождество, следовательно, данная функция является решением данного ДУ.

Дифференциальные уравнения первого порядка

и методы их решения. Метод изоклин (графическое решение)

Геометрическое истолкование ДУ первого порядка. Уравнение устанавливающее связь (зависимость) между координатами точки и угловым коэффициентом касательной интегральной кривой, проходящей через эту точку. Следовательно, ДУ дает совокупность направлений (поле направлений) на плоскости Оху.

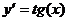
Поле направлений изображаетсяпри помощисистемы чёрточек или стрелок с углом наклона .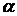

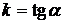
Кривые (где ), в точках которых наклон поля имеет постоянное значение, равное k, называются изоклинами. Построив изоклины и поле направлений, можно приближённо нарисовать интегральные кривые, рассматривая последние как кривые, которые в каждой своей точке имеют заданное направление поля.

Пример 2.Методом изоклин построить приближенно поле интегральных кривых для дифференциальног уравнения .

Решение. Здесь изоклинами являются прямые линии:

, где

, , ;

, , .

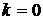
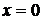
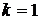
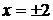
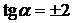
На каждой из прямой изображаем систему черточек под найденным углом. Проводя линии таким образом, чтобы черточки являлись касательными к интегральным кривым, получим параболы (рис. 12)

«ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Руководство к решению задач 1 2 Молдавский государственный университет Кафедра дифференциальных уравнений Д. Н. Чебан Обыкновенные дифференциальные . »

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ

УРАВНЕНИЯ

Руководство к решению задач

Молдавский государственный университет

Кафедра дифференциальных уравнений

Обыкновенные дифференциальные уравнения

Руководство к решению задач

Учевное пособие Утверждено Советом факультета математики и информатики Кишинев–2001 3 CZU 517.9 (075.8) C 33 Рекомендовано кафедрой дифференциальных уравнений Рецензенты:

Б. А. Щербаков, доктор хабилитат физико–математических наук, профессор университар;

Н. И. Вулпе, доктор хабилитат физико–математических наук, профессор университар.

Prezenta carte este o lucrare didactic la cursul de ecuatii diferentiale a ordinare. Ea contine circa 400 de exerciii i probleme rezolvate, incluse ts n cunoscuta culegere de probleme a profesorului A.F. Filippov. Scopul principal al crii este de a contribui la o sire profund a materialului teoretic, at nsu a dezvoltare a gndirii matematice concrete a studenilor, asimilarea aptitua t dinilor de rezolvare a exerciiilor i problemelor, coninutului zic al lor.

t s t Cartea este destinat studenilor de la prolurile matematic i zic, a t as a informatic i cibernetic de la universiti, precum i studenilor de la as a at s t instituii pedagogice i tehnice de aamnt superior cu studierea aprot s nvt a fundat a matematicii. Ea va util i unui cerc mai larg de cititori, inclusiv a as pentru autodidaci cursul de ecuaii difereniale, pentru profesorii tineri, t n t t care si ncep activitatea pedagogic instituii de aamnt superior.

a n t nvt a Д. Н. Чебан. Обыкновенные дифференциальные уравнения. Руководство к решению задач: Учебное пособие.– Кишинев: Молдавский госуниверситет, 2001.– с.

ISBN 9975–917–66– c Молдавский государственный университет, c Д. Н. Чебан, Оглавление Предисловие Обозначения Глава 1. Дифференциальные уравнения первого порядка 1. Основные понятия 2. Уравнения с разделяющимися переменными 3. Геометрические и физические задачи 4. Однородные уравнения 5. Линейные уравнения первого порядка 6. Уравнения в полных дифференциалах. Интегрирующий множитель 7. Существование и единственность решения 8. Уравнения, не разрешенные относительно производной 9. Разные уравнения первого порядка Глава 2. Дифференциальные уравнения высших порядков 1. Уравнения, допускающие понижение порядка 2. Линейные уравнения с постоянными коэффициентами 3. Линейные уравнения с переменными коэффициентами Глава 3. Системы дифференциальных уравнений 1. Линейные системы с постоянными коэффициентами Глава 4. Приближенное решение дифференциальных уравнений.

Уравнения в частных производных первого порядка 1. Зависимость решения от начальных условий и параметров.

Приближенное решение дифференциальных уравнений 3. Уравнения в частных производных первого порядка

ПРЕДИСЛОВИЕ

Настоящая книга является учебным пособием по обыкновенным дифференциальным уравнениям в их прикладном аспекте для студентов физико–математического профиля, а также информатики и кибернетики университетов, и для студентов педагогических и технических вузов с повышенным уровнем преподавания математики. Она будет полезной и более широкому кругу лиц, в том числе самостоятельно изучающим дифференциальные уравнения, и молодым преподавателям, начинающим свою практическую деятельность в высших учебных заведениях.

Книга содержит свыше 400 решенных примеров и задач, взятых из известного задачника профессора А. Ф. Филиппова.

Главная цель настоящей книги–способствовать глубокому усвоению теории, развитию конкретного математического мышления студентов, привитию им навыков решения примеров и задач, пониманию их физической сущности.

В начале каждого параграфа в конспективной форме приводится необходимый теоретический материал.

Книга полностью охватывает все разделы курса обыкновенных дифференциальных уравнений для университетов: дифференциальные уравнения первого порядка, дифференциальные уравнения высших порядков, системы дифференциальных уравнений, устойчивость и т. д.

Она написана на основе более 20–летнего опыта проведения автором практических и лабораторных занятий по курсу дифференциальных уравнений со студентами факультета математики и информатики и физического факультета Молдавского государственного университета.

Все отзывы, замечания и пожелания относительно данного пособия с признательностью будут приняты по адресу: Республика Молдова, МД 2009, г. Кишинев, ул. А. Матеевича, 60, Молдавский государственный университет, факультет математики и информатики.

Д. Н. Чебан Май 2001 г.

г. Кишинев e-mail: cheban@usm.md Настоящая книга написана при частичной финансовой поддержке НПК «Nivel» S+ (S ) подмножество всех неотрицательных f (·, x) частное отображение, задаваемое функцией |x| или ||x|| норма элемента x;

B(x0, r) открытый шар с центром в точке x B[x0, r] замктнутый шар с центром в точке x0 и множество состоящее из элементов x, y. z;

lim xn предел последовательности;

ОБОЗНАЧЕНИЯ

Дифференциальные уравнения первого порядка 1.1. Изоклины. Уравнение определяет в каждой точке (x, y) области G R2, где определена функция f, значение y, т.е. угловой коэффициент касательной к интегральной кривой в этой точке.

Определение 1. Если через каждую точку области G проходит некоторая прямая, то говорят, что в области G задано поле направлений.

Таким образом, дифференциальное уравнение (1) определяет поле направлений.

Определение 2. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и то же направление. Следовательно, уравнение изоклины имеет вид f (x, y) = k, где k- постоянная.

Для того чтобы приближенно построить решения уравнения (1), можно начертить достаточно густую сеть изоклин, придавая k близкие числовые значения, а затем провести решения.

Замечание 1. 1. Нулевая изоклина f (x, y) = 0 дает уравнение линий, на которых могут располагаться точки максимума и минимума интегральных кривых.

2. Геометрическое место точек перегиба интегральных кривых уравнения (1), если они существуют, определяется уравнением 3. Точки пересечения двух или нескольких изоклин являются особыми точками дифференциального уравнения (1), так как в них направление интегральных кривых становится неопределенным.

6 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

В задачах 1-5 с помощью изоклин начертить (приближенно) решения данных уравнений.

Решение. Для получения уравнения изоклин положим y = k (k R), тогда y x2 = k или y = x2 + k.

Изоклинами является семейство всех парабол, полученных параллельным переносом вдоль оси Oy параболы y = x2. При k = 0 получаем изоклину y = x2. Эта парабола делит плоскость xOy на две части, в каждой из которых производная y имеет один и тот же знак.

Интегральные кривые, пересекая параболу y = x2, переходят из области убывания функции y в область ее возрастания, и наоборот, а значит, на этой параболе находятся точки экстремума интегральных кривых. А именно, точки параболы y = x2 с отрицательными абсциссами являются точками минимума, а с положительными абсциссами — точками максимума (см. задачу 6).

Уравнение определяет точки перегиба, а неравенства e x2 2x 0 и y x 2x 0 определяют области, в которых интегральные кривые вогнуты, и,соответственно, выпуклы (см. рис. 1).

На рис. 1 пунктиром отмечена парабола y = x2 + 2x, точки которой являются точками перегиба интегральных кривых данного уравнения.

Легко проверить, что функция y = x2 + 2x + 2 является решением исходного уравнения.

Проведенное исследование позволяет нам приближенно построить интегральные кривые данного уравнения.

1В скобках указаны соответствующие номера из книги А.Ф.Филиппова, Сборник задач по дифференциальным уравнениям, М., Наука, 1992.

Решение. Заметим, что интегральные кривые расположены симметрично относительно начала координат. Последнее следует из того, что при замене x на x и y на y исходное уравнение не изменяется.

Поэтому для полного представления о поведении интегральных кривых достаточно исследовать их в верхней (или нижней) полуплоскости.

Полагая y = k, получим уравнение семейства изоклин:

Таким образом, изоклины составляют семейство всех окружностей с центром в начале координат.

При k = 0 получаем изоклину x2 + y 2 = 2. Эта окружность радиуса r = 2 делит плоскость на две части, в каждой из которых производная y имеет один и тот же знак.

Интегральные кривые, пересекая окружность x2 + y 2 = 2, переходят из области убывания функции y в область ее возрастания, и наоборот, значит, на этой окружности находятся точки экстремума интегральных кривых. А именно, точки окружности x2 + y 2 = 2 с отрицательными абсциссами являются точками максимума, а с положительными абсциссами – точками минимума.

Уравнение определяет точки перегиба, а неравенства определяют область, в которой интегральные кривые вогнуты и, соответственно, выпуклы (см. рис. 2). Отметим, что равенством (2) определяется некоторая кривая на плоскости, которая симметрична относительно начала координат, так как при замене x на x и y на y уравнение (2) не изменяется. Для построения кривой, задаваемой равенством (2), можно перейти к полярным координатам. Тогда из (2) имеем (3) Касательные к интегральным кривым данного уравнения, проведенные в точках окружности x2 + y 2 = 2(1 + k) k 1, образуют с осью абсцисс угол, равный arctgk. Начертив несколько изоклин и поле направлений, строим приближенно интегральные кривые уравнения (см. рис.

8 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Решение. Заметим, что интегральные кривые данного уравнения расположены симметрично как относительно оси абсцисс, так и относительно оси ординат. Это следует из того, что при замене в этом уравнении x на x или y на y оно не изменяется. Поэтому для полного представления о поведении интегральных кривых достаточно исследовать их в I квадранте координатной плоскости.

Для получения уравнения изоклин положим y = k (k R), тогда ky + x = 0 или x = ky.

Изоклинами являются все прямые, проходящие через начало координат. При k = 0 получаем изоклину x = 0. Эта прямая (ось Oy) делит всю плоскость на две части, в каждой из которых производная y имеет один и тот же знак. Интегральные кривые, пересекая ось Oy, переходят из области убывания функции y = y(x) в область ее возрастания и наоборот, значит, на этой оси находятся и точки экстремума интегральных кривых, а именно: точки оси Oy с положительными ординатами, являющиеся точками максимума, и с отрицательными ординатами, являющиеся точками минимума (см. Задачу 6).

Касательные к интегральным кривым данного уравнения, проведенные в точках прямой x = ky, образуют с осью абсцисс угол, равный arctgk. Начертив несколько изоклин и поле направлений, строим приближенно интегральные кривые уравнения (см. рис. 3).

Задача 4. (7). xy + y = 0.

Решение. Отметим, что также как и в предыдущем примере, интегральные кривые расположены симметрично относительно осей координат. Поэтому ограничимся исследованием поведения интегральных кривых в I квадранте координатной плоскости.

Уравнение изоклин имеет вид kx + y = 0 или y = kx.

Изоклинами является семейство всех прямых, проходящих через начало координат. При k = 0 получаем изоклину y = 0. Легко убедиться, что y = 0 также является интегральной кривой данного уравнения.

Заметим, что производная y в первой четверти координатной плоскости является отрицательной и, следовательно, функция y = y(x) является убывающей на интервале (0, +).

Касательные к интегральным кривым данного уравнения, проведенные в точках прямой y = kx, образуют с осью абсцисс угол, равный arctgk. Начертив несколько изоклин и поле направлений, строим приближенно интегральные кривые данного уравнения (см. рис. 4).

Решение. Уравнение семейства изоклин для данного уравнения имеет вид x ey = k, x = ey + k.

Таким образом, изоклинами являются все экспоненты, полученные параллельным переносом вдоль оси Ox экспоненты x = ey. Эта экспонента делит плоскость xOy на две части, в каждой из которых производная y имеет один и тот же знак.

Пусть y = y(x) – некоторое решение данного уравнения, пересекающее экспоненту x = ey в точке (x0, y0 ). Так как

10 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

где f (x, y) = x ey, то y = y(x) в точке x = x0 имеет минимум. Таким образом, точки экспоненты x = ey являются точками минимума решений уравнения y = x ey.

Уравнение определяет точки перегиба, а неравенства x ey + ey и x ey + ey определяют области, в которых интегральные кривые вогнуты и, соответственно, выпуклы (см. рис. 5).

Касательные к интегральным кривым данного уравнения, проведенные в точках экспоненты x = ey + k, образуют с осью абсцисс угол, равный arctgk. Начертив несколько изоклин и поле направлений, строим приближенно интегральные кривые уравнения (см. рис. 5).

Задача 6. (15). Написать уравнение геометрического места точек (x, y), являющихся точками максимума или минимума решений уравнения y = f (x, y). Как отличить точки максимума от точек минимума?

Решение. Пусть y = (x) – некоторое решение уравнения и x = x0 точка его максимума или минимума, тогда где y0 = (x0 ). Если (x0, y0 ) точка экстремума некоторого решения уравнения (4), то (5) Таким образом, условие (5) является необходимым для того, чтобы точка (x0, y0 ) была точкой экстремума некоторого решения уравнения (4). В общем случае условие (5) не гарантирует, что точка (x0, y0 ) Mf будет точкой экстремума какого-либо решения уравнения (4). Сказанное выше подтверждается следующим примером.

Рассмотрим уравнение (6) Легко проверить, что y = x3 является решением уравнения (6) и (0, 0) Mf = <(x, y) R2 | y = x3 3x2 >(см. рис. 6). Кроме того, через точку (0, 0) проходит решение y = x3, однако точка (0, 0) не является его точкой экстремума.

Пусть теперь x = x0 — точка максимума решения y = (x) и (x0 ) 0, тогда Таким образом, если (x0, y0 ) R2 — точка экстремума некоторого решения уравнения (4) и то точка (x0, y0 ) является точкой максимума некоторого решения уравнения (4). Аналогично устанавливается, что точка экстремума (x0, y0 ) R2 решения y = (x), удовлетворяющая условию

12 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

является точкой минимума этого решения.

Из сказанного выше следует, что любое решение системы является точкой минимума некоторого решения уравнения (4), а любое решение системы является точкой максимума некоторого решения уравнения (4). Обратное утверждение неверно.

Задача 7. (16). Написать уравнение геометрического места точек перегиба графиков решений уравнений Решение. а) Геометрическое место точек перегиба интегральных кривых уравнения (1), если они существуют, определяется уравнением так как y (x) = (x, y(x)) + (x, y(x))y (x).

2xy 3 = (1 x2 )(2×2 2).

1.2. Составление дифференциального уравнения семейства кривых. Для того, чтобы построить дифференциальное уравнение, которому удовлетворяют кривые семейства надо продифференцировать равенство (7) n раз, считая y функцией от x, а затем из полученных уравнений и уравнения (7) исключить произвольные постоянные.

Задача 8. (17, 20, 24, 26). Составить дифференциальные уравнения данных семейств линий:

C = y /y и, следовательно, y = exy /y.

3) Дифференцируя равенство Cy = sin Cx по переменной x, мы получим систему поэтому y 2 + C 2 y 2 = 1. Из последнего равенства имеем C = ± 4) Дважды дифференцируя равенство (x a)2 + by 2 = 1, мы получим

14 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Исключая из второго и третьего уравнений этой системы параметры a и b, мы получим ( Задача 9. (30). Составить дифференциальное уравнение окружностей радиуса 1, центры которых лежат на прямой y = 2x.

Решение. Уравнение указанного семейства окружностей имеет вид (xa)2 +(y2a)2 = 1 (см. рис. 7). Дифференцируя по x это соотношение, находим 2(x a) + 2(y 2a)y = 0. Исключив из этих двух равенств параметр a, мы получим искомое уравнение:

или Задача 10. (32). Составить дифференциальное уравнение окружностей, касающихся одновременно прямых y = 0 и x = 0 и расположенных в I и III четвертях.

Решение. Уравнение данного семейства окружностей (см. рис. 8) имеет вид (x a)2 + (y a)2 = a2. Дифференцируя это равенство по x, находим 2(x a) + 2(y a)y = 0. Выражая из последнего равенства a, получим a = и, следовательно, Задача 11. (33). Составить дифференциальное уравнение всех парабол с осью, параллельной Oy и проходящей через начало координат.

Решение. Уравнение указанного семейства парабол имеет вид y = ax2 + bx (см. рис.9). Дважды дифференцируя по x это соотношение, находим y = 2ax + b и y = 2a. Исключив из этих равенств параметры a и b, мы получим искомое дифференциальное уравнение y = + x(y xy ) или x

16 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Задача 12. (35). Найти систему дифференциальных уравнений, которой удовлетворяют линии семейства ax + z = b, y 2 + z 2 = b2.

Решение. Дифференцируя по переменной x данные равенства, получим a + zx = 0 и 2yyx + 2zzx = 0.

Исключив из этих равенств параметры a и b, мы получим 1.3. Изогональные траектории.

Определение 3. Линии, пересекающие все кривые данного семейства под одним и тем же углом, называются изогональными траекториями.

Углы и наклона траектории и кривой к оси Ox связаны соотношением а. Пусть (1) — дифференциальное уравнение данного семейства кривых, есть уравнение семейства изогональных траекторий. Тогда Следовательно, если уравнение (1) написано и угол известен, то можно найти tg и затем записать дифференциальное уравнение изогональных траекторий. Если в дифференциальном уравнении данного семейства заменить y на значение q, определяемое равенством то получим дифференциальное уравнение семейства изогональных траекторий. В частности, дифференциальное уравнение ортогональных траекторий ( = 90 ) получается заменой в уравнении (1) y на 1/y.

б. Если уравнение данного семейства кривых написано в виде то при составлении уравнения изогональных траекторий можно обойтись без разрешения уравнения (8) относительно y. В этом случае в (8) надо заменить y на tg = tg ±, где tg = y — угловой коэффициент касательной к траектории.

в. Если уравнение семейства кривых задано в виде (x, y, C) = 0, то вначале нужно составить дифференциальное уравнение этого семейства и только после этого — дифференциальное уравнение изогональных траекторий.

г. В случае полярных координат в дифференциальном уравнении данного семейства следует заменить r /r (логарифмическая производная от r) на значение µ, определяемое равенством В частности, дифференциальное уравнение ортогональных траекторий получается заменой r /r на r/r.

Замечание 2. Может оказаться, что задача, заданная в декартовых координатах, проще решается в полярных координатах, или наоборот.

Задача 13. (37, 40, 46). Составить дифференциальные уравнения траекторий, пересекающих линии данного семейства под данным углом Решение. а) Сначала составим дифференциальное уравнение семейства кривых y = Cx4, для чего продифференцируем последнее равенство по x. Таким образом, y = 4Cx3. Исключив из этих равенств параметр C, мы получим y = 4y/x — дифференциальное уравнение заданного семейства кривых.

Заменив в полученном уравнении y на q = 1/y мы получим дифференциальное уравнение y = x/4y или 4yy = x.

б) Составим дифференциальное уравнение семейства кривых x2 + 2 = a2, для чего продифференцируем данное равенство по x, тогда получим 2x + 2yy = 0, т. е. y = x/y. Заменяя в полученном уравнении или Отметим, что семейство кривых, ортогональное к семейству решений уравнения (9), очевидно, также пересекает под углом 45 линии x2 +y 2 = a2. Дифференциальное уравнение этого семейства кривых получается из уравнения (9) заменой y на 1/y, т. е. y =. Таким образом, искомые траектории являются решениями дифференциальных уравнений в) Для составления дифференциального уравнения семейства кривых r = a sin, продифференцируем последнее равенство по. Тогда мы получим r = a cos и, следовательно,

18 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Заменяя в полученном уравнении r /r на µ, определяемое равенством получим дифференциальное уравнение изогональных траекторий или Семейство кривых, ортогональное к семейству решений уравнения (10), также пересекает под углом 45 линии r = a sin. Дифференциальное уравнение этого семейства получается из (10) заменой r /r на r/r, т.е.

Таким образом, изогональные траектории являются решениями дифференциального уравнения r = arctg( ± 45 ).

2. Уравнения с разделяющимися переменными 2.1. Уравнения вида y = f (x)g(y) и M (x)N (y)dx+ P (x)Q(y)dy = 0.

Определение 4. Уравнение вида называется уравнением с разделенными переменными.

Определение 5. Уравнение вида а также вида называется уравнением с разделяющимися переменными.

Для решения уравнения с разделяющимися переменными надо обе части умножить или разделить на такое выражение, чтобы в одну часть уравнения входил только x, в другую — только y, и затем проинтегрировать обе части.

Замечание 3. При делении обеих частей уравнения на выражение, содержащее неизвестные x и y, могут быть потеряны решения, обращающие это выражение в нуль.

Задача 14. (52). Решить уравнение

2. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ

тегрируя обе части этого уравнения, получим y 2 + 1 = (C + ln|x|)2.

Задача 15. (55). Решить уравнение y = 3 3 y 2, а также найти решения, удовлетворяющие условию y(3) = 0.

получим уравнение с разделенными переменными = 3dx. Интегриy руя обе части последнего уравнения, получаем (11) Отметим, что в найденное семейство функций не входит y = 0, мы потеряли его при делении на 3 y 2.

Полагая в (11) x = 3, будем иметь 0 = (C + 3)3, откуда находим C = 3. Таким образом, семейство решений (11) уравнения y = 3 3 y содержит единственное решение y = (x 3)3, удовлетворяющее начальному условию y(3) = 0. Очевидно, тривиальное решение y = 0 также удовлетворяет этому условию.

Замечание 4. Отметим, что уравнение y = 3 3 y 2 с начальным условием y(3) = 0 кроме двух указанных выше решений, допускает и семейство решений вида:

где и — произвольные действительные числа, удовлетворяющие указанным выше условиям (см. рис. 10).

2.2. Уравнения вида y = f (ax+by+c). Дифференциальное уравнение вида где a, b и c — постоянные, заменой переменных z = ax + by + c приводится к уравнению с разделяющимися переменными.

Задача 16. (62). Решить уравнение y = cos(y x).

20 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Решение. Обозначим через z = y x, тогда уравнение y = cos(y x) приводится к виду Прежде всего заметим, что уравнение (12) допускает семейство решений zk = 2k (k = 0, ±1, ±2. ). Остальные решения уравнения (12) можно получить, разделив обе части уравнения (12) на cos z и проинтегрировав обе части полученного уравнения, т. е.

Таким образом, решениями уравнения y = cos(y x) являются функции Задача 17. (66). Найти решение уравнения x2 y cos 2y = 1, удовлетворяющее условию y(+) =.

Решение. Запишем уравнение x2 y cos 2y = 1 в следующем виде которое приводится к уравнению Интегрируя обе части последнего уравнения, получаем

2. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ

Кроме семейства (13), очевидно, решениями данного уравнения являются и функции yk = + 2k (k Z).

Из равенства (13) имеем где m – некоторое целое число. Так как y(+) =, то для искомого решения число m может равняться только двум. Итак, и, следовательно, = arctgC + 2. Поэтому C = 1 и y(x) = arctg( + 1) + 2.

Задача 18. (68.б). Найти ортогональные траектории к линиям y = Cex.

Решение. Прежде всего составим дифференциальное уравнение семейства линий y = Cex, для чего продифференцируем последнее равенство по x. Тогда получим y = Cex и, следовательно, Заменив в уравнении (15) y на, получим дифференциальное уравнение ортогональных траекторий к линиям y = Cex. Уравнение (16) является уравнением с разделяющимися переменными; интегрируя его, получим Задача 19. (69*). Показать, что каждая интегральная кривая уравy2 + нения y = имеет две горизонтальные асимптоты.

Решение. Данное дифференциальное уравнение является уравнением вида Интегрируя обе его части, получим где F и G — какие-нибудь первообразные функции и соответственно. Пусть y — решение уравнения y =, удовлетx4 + воряющее условию y(x0 ) = y0 (x0, y0 — произвольные действительные

22 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

числа). Тогда из (17) получим из (18) получаем му из равенства (19) следует ограниченность на R = (, +) функции y, определенной равенством (19). Так как y = 0 то функция y(x) является монотонно возрастающей, и в силу ее ограниченности на R существуют конечные пределы a = lim y(x) и b = lim y(x).

3.1. Геометрические задачи. Если требуется найти уравнение кривой по заданному свойству ее касательной (или нормали, или подкасательной, или поднормали) в любой ее точке, то выражают все упомянутые в задаче величины через x, y, и y. Используя известные формулы из геометрии, устанавливают связь между x, y, и y, где x, y — координаты точки касания. Этим будет найдено дифференциальное уравнение искомой кривой. Решая полученное уравнение, можно найти искомую кривую y = y(x).

Задача 20. (71). Найти кривые, для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная a2.

Решение. Пусть y = y(x) — уравнение искомой кривой в прямоугольной системе координат (см. рис. 11). Согласно условию задачи, площадь треугольника ABC равна a2. С другой стороны,

3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ЗАДАЧИ

Полученное уравнение является уравнением с разделяющимися переменными. Решая его, находим Задача 21. (73). Найти кривые, обладающие следующим свойством:

отрезок оси абсцисс, отсекаемый касательной и нормалью, проведенными из произвольной точки кривой, равен a2.

Решение. Пусть y = y(x) — уравнение искомой кривой в прямоугольной системе координат (см. рис. 12).

24 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

BD = и AD = yy и, следовательно, Разрешая последнее уравнение относительно y, имеем Полагая y 2 = u2 + a2, из последнего уравнения получим или, возвращаясь к старой переменной, имеем Задача 22. (75). Найти кривые, обладающие следующим свойством:

если через любую точку кривой провести прямые, параллельные осям координат, до встречи с этими осями, то площадь полученного прямоугольника делится кривой в отношении 1 : 2.

Решение. Пусть y = y(x) — уравнение искомой кривой в прямоугольной системе координат (см. рис. 13).

Пусть B(x, y) — произвольная точка на графике функции y = y(x), тогда площадь S прямоугольника ABCO равна xy, а площадь криволиx нейной трапеции BCD равна S1 = y( )d. Согласно условию задачи

3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ЗАДАЧИ

S1 : S = 1 : 3 и, следовательно, 3 y( )d = xy. Дифференцируя обе части последнего равенства, получим 3.2. Физические задачи. В физических задачах надо прежде всего следует решить, какую из величин взять за независимую переменную, а какую — за искомую функцию. Затем надо выразить, насколько изменится искомая функция y, когда независимая переменная x получит приращение x, т. е. выразить разность y = y(x + x) y(x) через величины, о которых говорится в задаче. Разделив эту разность на x и переходя к пределу при x 0, получим дифференциальное уравнение, из которого можно найти искомую функцию, т. е. зависимость скорости изменения величины y в точке x (производной y (x) от x и y(x)). Во многих случаях указанная зависимость определяется на основании закона или экспериментального факта, установленного в той или иной области естествознания. Иногда дифференциальное уравнение можно составить более простым путем, воспользовавшись физическим смыслом производной (y есть скорость изменения величины y). В большинстве задач содержатся условия, с помощью которых можно определить значения постоянных, входящих в общее решение дифференциального уравнения.

Задача 23. (77). Сосуд объемом в 20 л содержит воздух (80% азота и 20% кислорода). В сосуд втекает 0,1 л азота в секунду, который непрерывно перемешивается, и вытекает такое же количество смеси.

Через сколько времени в сосуде будет 99% азота?

Решение. Примем за независимую переменную время t, а за искомую функцию y(t) — количество азота в сосуде через t секунд после начала опыта. Найдем насколько изменится количество азота за промежуток времени от момента t до момента t + t. За одну секунду поступает 0, л азота, а за t секунд — 0, 1 · t литров; с другой стороны, за время t из сосуда вытекает такое количество смеси, в котоpой содержалось бы 0, 1t · л азота, если бы за время t содержание азота в сосуде не менялось. Но так как оно за это время меняется на величину, бесконечно малую при t 0, то в вытекающих 0, 1 · t литрах смеси содержится

26 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Итак, за промежуток времени [t, t+t] в сосуд втекает 0, 1·t литров азота, а вытекает 0, 1 · t · л. Приращение количества азота за это время y = y(t + t) y(t) равно разности найденных величин, т. е.

Разделив обе части равенства (20) на t и переходя к пределу, когда t 0, мы получим в левой части производную y (t), а в правой части Итак, мы получим дифференциальное уравнение Решая его, получим (21) Так как при t = 0 азота в сосуде было 16 л, то y(0) = 16. Полагая в (21) t = 0, найдем y(0) = 20 + c = 16 и, следовательно, C = 4.

Подставляя найденное значение C в (21), получим y(t) = 20 4 · e Обозначим через t0 момент времени, когда в сосуде будет 99% азота, т. е. 19,8 л; тогда y(t0 ) = 19, 8 л. Полагая t = t0 в (21), мы получим 200 = 19, 8 и, следовательно, t0 = 200 ln 5 · 102 600 сек = 20 4e мин.

В задачах 22 и 23 считается, что скорость остывания (или нагревания) тела пропорциональна разности температур тела и окружающей среды.

Задача 24. (80). Тело охладилось за 10 минут от 100 до 60. Температура окружающего воздуха поддерживается равной 20. Когда тело остынет до 25 ?

Решение. Обозначим через T (t) температуру тела в момент времени t. Так как в условиях задачи скорость изменения температуры тела пропорциональна разности температур тела и окружающей среды, то где 0 — коэффициент пропорциональности. Полученное уравнение является дифференциальным уравнением с разделяющимися переменными. Решая его, находим Учитывая условие T (0) = 200, находим C = 80 и, следовательно,

3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ЗАДАЧИ

Для определения коэффициента воспользуемся условием T (10) = 60, т.е. 20 + 80e10 = 60, откуда имеем Используя полученный закон изменения температуры тела, найдем искомое время:

Задача 25. (83). Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1,5м/сек, через 4 сек скорость ее 1м/сек. Когда скорость уменьшается до 1см/сек? Какой путь может пройти лодка до остановки?

Решение. Пусть y = y(t) — скорость лодки в момент времени t тогда v(0) = 1, 5 м/сек. Согласно второму закону Ньютона, my (t) = F (t), где F (t) — сила, действующая на лодку, а m — ее масса. По условию задачи, F (t) = ky(t), где k 0 — коэффициент пропорциональности, а знак минус означает, что сила направлена против движения (на уменьшение скорости). Поэтому дифференциальное уравнение движения лодки есть Его общее решение: y(t) = Ce C = 1, 5 и y(0) = 1, 5e скорость лодки y(t) = 1, 5e 4 3 = (2/3) 4. Время t0, через которое скорость лодки будет равна 1см/сек, находим из уравнения т.е. t0 = 4(1+ ) 24 сек. Длину пути, пройденного лодкой, вычислим по формуле Ооткуда следует, что лодка может пройти до остановки путь, не больший

28 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

В задаче 26 используется закон радиоактивного распада:

количество вещества, распадающегося за единицу времени, пропорционально количеству вещества, имеющегося в рассматриваемый момент времени.

Задача 26. (84). За 30 дней распалось 50% первоначального количества радиоактивного вещества. Через сколько времени его останется 1% от первоначального количества?

Решение. Пусть y(t) — количество радиоактивного вещества в момент времени t, y(0) = y0. Так как скорость радиоактивного распада пропорциональна количеству вещества, то y (t) = ky(t), k 0. Решая последнее уравнение, находим y(t) = y0 ekt. По условию задачи y(30) = y0 и, следовательно, (22) Из равенства (22) находим k = ln 2 поэтому y(t) = y0 2 30.

Обозначим через t0 момент времени, когда останется 1% от первоначального количества радиоактивного вещества, тогда y(t0 ) = y0, т.е.

(23) Из равенства (23) находим t0 = 200 дней.

Задача 27. (87). Количество света, поглощаемогое слоем воды малой толщины, пропорционально количеству падающего на него света и толщине слоя. Слой воды толщиной 35 см поглощает половину падающего на него света. Какую часть света поглотит слой толщиной в Решение. Пусть Q = Q(h) — световой поток, падающий на поверхность воды на глубинуе h. При прохождении через слой воды толщиной dh поглощаемый световой поток dQ равен dQ = kQdh, где k — коэффициент пропорциональности. Отсюда Q(h) = Cekh.

Пусть первоначальный световой поток равен Q0. Тогда из начального условия Q(0) = Q0 находим, что C = Q0, и поэтому Q(h) = Q0 ek·h.

По условию, Q(0, 35) = Q0, поэтому Q0 = Q0 e0,35·k, откуда k = 0, дойдет световой поток Q(2) = Q0 2 7 = Q0 2 7 Q0 0, 002.

3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ЗАДАЧИ

Таким образом, до глубины 2м дойдет около 2% первоначального светового потока, и, следовательно, поглотится 98% светового потока.

Задача 28. (88). Парашютист прыгнул с высоты 1,5 км, а раскрыл парашют на высоте 0,5 км. Сколько времени он падал до раскрытия парашюта? Известно, что предельная скорость падения человека в воздухе нормальной плотности составляет 50м/сек. Изменением плотности в зависимости с от высотыой пренебречь. Сопротивление воздуха пропорционально квадрату скорости.

Решение. В дифференциальном уравнении движения парашюта m dv dt = F сила F является равнодействующей двух противоположных сил:

силы тяжести FT = mg и силы сопротивления воздуха, равной Fmp = v 2 ( 0). Поэтому дифференциальное уравнение движения есть m dv dt = mgv 2 или dv = gkv 2, где k = m. Разделяя переменные и интегрируя, получаем Если t = 0, то v = 0 и, следовательно, C = 0 и получаем Из последнего равенства выразим v как функцию времени t:

Согласно условию задачи v(+) = 50, из равенства (24) имеем v(+) 50th 5.

Интегрируя, имеем Отсюда при начальном условии t = 0, s = 0 постоянная C = 0 и, следовательно, S = ln ch( g·t) = 250 ln ch. Если через t0 обозначить время падения парашютиста, то согласно условию задачи S(t0 ) = 1000, т.е.

Из последнего равенства имеем

30 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Задача 29. (89). Футбольный мяч весом 0,4 кг брошен вверх со скоростью 20 м/сек. Сопротивление воздуха пропорционально квадрату скорости и равно 0,48 Г при скорости 1 м/сек. Вычислить время подъема мяча и наибольшую высоту подъема. Как изменятся эти результаты, если пренебречь сопротивлением воздуха?

Решение. Для составления дифференциального уравнения воспользуемся вторым законом Ньютона: ma = mg + Fmp. В условиях задачи Fmp = kv 2, где k 0 — коэффициент пропорциональности. Так как a = v, то имеем Положим k0 = kg. По условию задачи kv0 = 0, 0048, где v0 = 1м/сек, поэтому k = 0, 00048 и, следовательно, k0 = 0, 012. Интегрируя уравнение dv = g + k0 v 2, получим t + C = gk arctg k0 v или где g = 10 и k0 = 0, 012. Пусть t0 — время подъема мяча на наибольшую высоту, тогда v(t0 ) = 0, т.е. t0 = C. Для нахождения C воспользуемся начальным условием v(0) = 20, тогда 20 = k0 tg( gk0 C) и, следоваk Поскольку h(0) = 0, то C0 = k0 ln cos[C gk0 ] и, следовательно, h(t) = k0 ln cos[C gk0 ] + k0 ln cos[ gk0 (C t)]. Поэтому Если пренебречь сопротивлением воздуха, то v = g, v(t) = gt + C1.

Так как v(0) = 20, то C1 = 20 и, следовательно, v(t) = gt + 20. Откуда v(t0 ) = 0, если t0 = 2, а h(t) = g t2 +20t+C2. Так как h(0) = 0, то C2 = 0, и, следовательно, h(t) = g t2 + 20t. Откуда имеем hmax = h(2) = 20.

Истечение жидкости через отверстие в сосуде. Скорость истечения жидкости через малое отверстие в сосуде, находящееся на расстоянии h, ниже уровня жидкости в сосуде, без учета трения, равна скорости свободного падения тела с высоты h, т.е. 2gh. С учетом трения зависимость скорости v от h определяется законом Торричелли: v =

3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ЗАДАЧИ

µ 2gh, где g — ускорение свободного падения; µ — так называемый коэффициент расхода, который определяется эмпирически и зависити от жидкости. Для воды µ = 0, 62, для керосина µ = 0, 6.

Задача 30. Сосуд, площадь S = S(h) поперечного сечения которого есть известная функция высоты h, наполнен жидкостью до уровня H. В днище сосуда имеется отверстие площадью, через которое жидкость вытекает. Определить время t, за которое уровень жидкости понизится от начального положения H до произвольного уровня 0 h H и время T полного опорожнения сосуда.

Решение. Пусть высота жидкости в сосуде в некоторый момент t равна h. Количество жидкости V вытекающейе из сосуда за промежуток времени [t, t + t], можно подсчитать как объем цилиндра с площадью основания и высотой V (h): V = V (h)t. Этот же объем жидкости может быть вычислен другим способом. Вследствие утечки жидкости ее уровень h в сосуде понизится на величину h, следовательно, V = S(h)h. Приравнивая оба выражения для V имеем S(h)h = V (h)t. Разделив обе части последнего равенства на t и переходя к пределу при t 0 получим дифференциальное уравнение, описывающее зависимость уровня воды в сосуде от времени:

Подставляя вместо V (h) его значение, согласно закону Торричелли, и разделяя в этом уравнении переменные, получим и, следовательно, При полном опорожнении сосуда h = 0, поэтому время T опорожнения сосуда определяется по формуле Задача 31. (91). За какое время вытечет вся вода из цилиндрического бака с диаметром 2r = 1, 8м и высотой H = 2, 45 м через отверстие в днище диаметром 2r0 = 6см? Ось цилиндра вертикальна.

Решение. Площадь поперечного сечения S = S(h) в данном случае постоянна и равна r2, площадь отверстия = r0 (см. рис. 14).

32 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Согласно формуле (25), время опорожнения сосуда Задача 32. (92). Решить предыдущую задачу в предположении, что ось цилиндра расположена горизонтально, а отверстие находится в самой нижней части цилиндра.

Решение. Площадь поперечного сечения S = S(h) в этом случае зависит от h и определяется по формуле S(h) = 2H · (2R h)h (см.рис.

15), а площадь отверстия = r0. Согласно формуле (25), время опорожнения

3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ЗАДАЧИ

сосуда Задача 33. Определить зависимость p = p(h) давления p от высоты h над уровнем моря.

Решение. Напомним, что за величину атмосферного давления принимается вес вертикального столба воздуха с площадью сечения S = 1см. Следовательно, разность численно равна весу столбика воздуха от высоты h до высоты h + h (см. рис.16), т.е. h(h) = m · g где m — масса этого столбца. Объем столбика равен V = Sh = h. Поэтому — если средняя плотность воздуха в столбике равна cp., то m = cp h, откуда p(h) = gcp h и, следовательно, Обозначим плотность воздуха на высоте h через (h); тогда при h 0, cp (h), и из равенства (26) получаем дифференциальное уравнение в котором, однако, функция (h) также неизвестна.

Предположим теперь, что температура воздуха одна и та же во всех слоях атмосферы. Тогда из закона Бойля-Мариотта или из уравнения

34 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

газового состояния легко вывести, что давление пропорционально плотности2:

Из (27) и (28) получаем окончательное дифференциальное уравнени Интегрируя уравнение (29), получаем (30) где p0 — атмосферное давление на уровне моря, т.е. p0 = p(0).

Итак, давление убывает с высотой по показательному закону, в соответствии с полученной так называемой барометрической формулой.

2pV = RN, откуда p = RT = RT · M = bg, b = RT, R — универсальная газовая постоянная, M — молярная масса газа.

3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ЗАДАЧИ

Полученная нами формула «отказывает»при высотах, сравнимых по величине с радиусом Земли. И связано это не только с тем, что мы пренебрегли изменением температуры с высотой, но и с изменением ускорения свободного падения.

Отметим, что в данном случае дифференциальное уравнение описывает не физический процесс, а просто изменение одной физической величины p в зависимости от другой h.

Задача 34. (97). Найти атмосферное давление на высоте h, если на поверхности земли давление равно 1кГ/см2 и плотность воздуха 0,0012г/см. Использовать закон Бойля-Мариотта, в силу которого плотность пропорциональна давлению (т.е. пренебречь изменением температуры воздуха с высотой).

Решение. Согласно предыдущему упражнению, атмосферное давление на высоте h определяется по формуле (30), где p0 — атмосферное давление на уровне моря, b = p0 /. В условиях нашей задачи p0 = 1кГ/см2, = 0, 0012г/см3 и, следовательно, p(h) = e0,12h (кГ/см2 ).

Задача 35. (100). Масса ракеты с полным запасом топлива равна M, без топлива — m, скорость истечения продуктов горения ракеты равна c, начальная скорость ракеты равна нулю. Найти скорость ракеты после сгорания топлива, пренебрегая силой тяжести и сопротивлением воздуха (формула Циолковского).

Решение. Для составления дифференциального уравнения движения ракеты воспользуемся уравнением Мещерского:

где v(t) — вектор абсолютной скорости материальной точки с переменной массой m(t) в момент времени t, F (t) — равнодействующая всех внешних сил, приложенных к точке переменной массы, R — реактивная сила (R = c, где c — относительная скорость истечения газов).

Выберем в качестве оси Ox прямую, по которой движется ракета. В проекции на эту ось дифференциальное уравнение (31) примет вид где m(t) — переменная масса ракеты, v(t) — ее скорость. Разделив в (32) переменные и интегрируя, получим v(t) = c ln m(t) + C. Значение постоянной C найдем, используя начальные условия v(0) = 0, m(0) = M.

Будем иметь C = c ln M и, следовательно, скорость ракеты изменяется со временем по закону

36 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Эта формула впервые получена К. Э. Циолковским и носит его имя (формула Циолковского).

В момент t = t0 полного сгорания масса m(t0 ) = m и из формулы (33) имеем v(t0 ) = c ln, где v(t0 ) — скорость ракеты в момент полного сгорания топлива.

4.1. Уравнения вида y = ( ).

Определение 6. Функция F (x, y) называется однородной, степени k, если для всех 0 выполняется равенство F (x, y) = k F (x, y).

Например, однородной функцией является любой однородный многочлен степени k. Однородными являются функции соответственно, степени 0, 1, 2, k.

Определение 7. Дифференциальное уравнение называется однородным, если f (x, y) — однородная функция степени нуль.

Однородное уравнение всегда можно представить в виде С введением новой искомой функции u = y/x уравнение (34) приводится к уравнению с разделяющимися переменными:

Если дифференциальное уравнение записано в симметрической форме (уравнение в дифференциалах), то оно будет однородным, если M (x, y) и N (x, y) — однородные функции одной и той же степени.

Пусть u = u0 есть корень уравнения (u) u = 0. Тогда решением однородного уравнения будет u = u0 или y = u0 x — прямая, проходящая через начало координат.

Замечание 5. При решении однородных уравнений необязательно приводить их к виду (34). Можно сразу делать подстановку y = ux.

Задача 36. (101). Решить уравнение Решение. Так как это уравнение является однородным, то полагаем y = ux. Тогда dy = udx + xdu. Подставляя эти выражения в уравнение (35), получим Решая полученное уравнение с разделяющимися переменными, находим Возвращаясь к старой переменной y, получаем y = x(1 + Cx). Кроме того, имеется решение x = 0, которое было потеряно при делении на x2.

Задача 37. (104). Решить уравнение 2×3 y = y(2×2 y 2 ).

Решение. Запишем данное уравнение в виде Так как уравнение (36) является однородным, то положим y = ux, тогда y = xu + u. Подставляя в уравнение (36) выражения для y и y получим Разделяем переменные и интегрированием находим Заменив u на y/x, получим Кроме того, имеется решение y = 0, которое мы потеряли при делении на u3.

Задача 38. (106). Решить уравнение (x2 + y 2 )y = 2xy.

Решение. Положим y = ux, тогда получим Последнее уравнение является уравнением с разделяющимися переменными. Интегрируя его, получим

38 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Возвращаясь к переменной y, имеем Задача 39. (108). Решить уравнение xy = y xey/x.

Решение. Разделив обе части данного уравнения на x, получим Положим y/x = u, тогда из последнего уравнения имеем u + xu = u eu, xu = eu. Разделив переменные и интегрируя, получим Задача 40. (111). Решить уравнение (y + xy)dx = xdy.

Решение. Положим y = u · x, тогда dy = udx + xdu и Разделив переменные и интегрируя, получим 4.2. Уравнения вида y = f ( a1 x+b1 y+c1 ). Уравнение вида приводится к однородному уравнению или уравнению с разделяющимися переменными.

b2 y+c2 = 0 пересекаются в некоторой точке (, ), и с помощью переноса начала координат уравнение (37) приводится к уравнению которое является однородным.

0 параллельны и при некотором k имеет место равенство a2 x + b2 y = k(a1 x + b1 y) и, следовательно, уравнение (37) имеет вид и приводится к уравнению с разделяющимися переменными заменой z = a1 x + b1 y.

Задача 41. (113). Решить уравнение (2x4y+6)dx+(x+y3)dy = 0.

Решение. Запишем данное уравнение в виде Рассмотрим систему линейных алгебраических уравнений Система (39) имеет единственное решение = 1, = 2. Произведем замену тогда уравнение (38) примет вид Уравнение (40) является однородным. Полагая = u, получим Интегрируя, найдем или Возвращаясь к переменным x, y, получим Кроме того, имеется решение y = x + 1, которое было потеряно при делении на u2 3u + 2 = (u 1)(u 2).

Задача 42. (115). Решить уравнение x y 1 + (y x + 2)y = 0.

Решение. Запишем данное уравнение в следующем виде:

Рассмотрим систему алгебраических уравнений

40 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

y 1 = 0 и x y 2 = 0 параллельны. Сделаем замену z = x y, тогда z = 1 y и, следовательно, Решая последнее уравнение, получим 2z z 2 /2 = x + C. Возвращаясь к переменным x, y, будем иметь (x y)2 4(x 2y) = 2x + C или (x y)2 2(x 2y) = C.

Задача 43. (117). Решить уравнение (y + 2)dx = (2x + y 4)dy.

Решение. Перепишем данное уравнение следующим образом:

Рассмотрим систему алгебраических уравнений Так как определитель этой системы то рассматриваемая система имеет единственное решение = 3 и = 2. Произведем замену, тогда уравнение (41) примет слеy = дующий вид:

Последнее уравнение является однородным. Полагая = u, получим Разделив переменные и интегрируя, получим Возвращаясь к переменным x, y, получим Решение. Разрешив относительно y данное уравнение, получим Так как система алгебраических уравнений имеет единственное решение = 3, = 3, то делаем в уравнении (42) замену тогда оно преобразуется к следующему виду Так как уравнение (43) является однородным, то, полагая = u, получим Разделив переменные в последнем уравнении и интегрируя его, получим 4.3. Уравнения, приводящиеся к однородному заменой y = z m. Иногда уравнение можно привести к однородному заменой переменной y = z m. Это имеет место в том случае, когда в уравнении все члены оказываются однородными, одинаковой степени, если переменной x приписать степень 1, переменной y — степень m, и производной y степень m 1.

Задача 45. (121). Решить уравнение x3 (y x) = y 2.

Решение. Делаем подстановку y = z m, y = mz m1 z, где m пока произвольное число, значение которого мы выберем позже. Подставляя в данное уравнение y и y, получим

42 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Заметим, что x3 z m1 имеет степень 3 + m 1 = m + 2, x4 имеет степень и z 2m имеет степень 2m. Полученное уравнение будет однородным в том случае, когда степени всех членов равны между собой, т. е. m + 2 = 4 = 2m. Эти равенства удовлетворяются одновременно, если m = 2.

Итак, при y = z 2 исходное уравнение принимает вид Положим теперь z = ux, z = u + xu. Тогда это уравнение примет вид Разделяя переменные в этом уравнении, получим Интегрируя, найдем Заменяя u2 через 2, получим Легко проверить, что функция y = x2 также является решением исходного уравнения, которое мы потеряли при делении на u2 1.

Задача 46. (123). Решить уравнение 2xdy + (x2 y 4 + 1)ydx = 0.

Решение. Произведем в данном уравнении замену y = z m, тогда оно примет следующий вид:

Полученное уравнение, очевидно, будет однородным, если 4m 1 = 1, т.е. m = 1/2.

Итак, пусть y = z 1/2, тогда имеем Полагая z = ux, получим Разделив переменные и интегрируя, получим u2 /2 = ln |x| + C. Возвращаясь к старым переменным, имеем x2 y 4 ln Cx2 = 1. Кроме того, легко проверить, что исходное уравнение допускает решение y = 0.

Задача 47. (125). Решить уравнение 2y + x = 4 y.

Решение. Замена y = z m приводит данное уравнение к виду которое будет однородным, если m 1 = 1 =, т.е. m = 2. Поэтому, если y = z 2, то имеем Так как последнее уравнение является однородным, то полагая z = ux, получим Возвращаясь к переменным x, y, имеем Задача 48. (127). Решить уравнение 2xy + y = y 2 x x2 y 2.

Решение. После замены y = z m уравнение примет вид 2mxz m1 z + zm = z 2m x x2 z 2m. Это уравнение будет однородным в том случае, если степени всех его членов равны между собой, т.е. 1 = 2 + 2m и m1+1 = m = 2m+1/2. Эти равенства удовлетворяются одновременно, если m = 1/2.

Произведем замену y = z 1/2 в исходном уравнении, тогда получим теперь z = ux, z = u + xu. Тогда это уравнение запишется следующим образом: u (u + xu ) + 1 = x ux Разделяя переменные, получим Интегрируя последнее уравнение, найдем Возвращаясь к переменным x, y, получаем Легко проверить, что данное уравнение допускает также Задача 49. (129). Решить уравнение 2y + (x2 y + 1)xy = 0.

44 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Решение. Легко проверить, что y = 0 является решением данного уравнения. Заменой y = z m данное уравнение сводится к виду Очевидно, уравнение 2z +(x2 z m +1)xmz = 0 является однородным, если m = 2. Итак, полагая y = z 2 (z = 0), получим Так как уравнение z ((x/z)2 + 1)xz = 0 является однородным, то заменой z = ux оно проводится к виду Разделив переменные в последнем уравнении и интегрируя, получим Возвращаясь к старым переменным, будем иметь и, следовательно, является общим решением исходного уравнения.

Задача 50. (130). Найти траектории, пересекающие кривые семейства y = x ln Cx под углом в 45, причем этот угол от касательной кривой до касательной к траектории отсчитывается в отрицательном направлении.

Решение. Составим вначале дифференциальное уравнение семейства кривых y = x ln Cx, для чего продифференцируем последнее равенство по переменной x. Таким образом, y = 1 + ln Cx. Исключив из этих равенств параметр C, мы получим Заменив в этом уравнении y на, получим уравнение семейства траекторий, пересекающих данное семейство кривых под углом в 45, т.

Полученное уравнение является однородным, поэтому положим y = zx, y = z x + z. Тогда будем иметь и возвращаясь к старым переменным, получим Задача 51. (132). Найти кривую, у которой расстояние любой касательной от начала координат равно абсциссе точки касания.

Решение. Пусть точка (x, y) лежит на искомой кривой y = y(x).

Касательная к этой кривой, проведенная в точке (x, y), находится от начала координат на расстоянии которое по условию задачи равно x. Поэтому искомая кривая является решением уравнения или y 2 2xyy + x2 y 2 = x2 + x2 y 2, т.е. 2xyy = y 2 x2. Это уравнение является однородным. Положим y = zx, тогда Возвращаясь к старым переменным, получим y 2 + x2 = Cx.

Задача 52. (135.а). Начертить приближенно интегральные кривые Решение. Для однородного уравнения y = (y/x) можно вычислить тангенс угла, под которым интегральные кривые пересекают луч y = kx.

Пусть M (x0, y0 ) — точка пересечения некоторой интегральной кривой с прямой y = kx (см. рис.17) и — величина угла между касательной и интегральной кривой в точке M (x0, y0 ) и осью абсцисс. Тогда угол между касательной к интегральной кривой и прямой y = kx равен, поэтому Точка M (x0, y0 ) лежит на прямой y = kx, следовательно,

46 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Таким образом, tg = 1+k(k). Запишем исходное уравнение в виде Для этого уравнения ( x ) = 2( x )2 ( x ) и, следовательно, (k) = 2k 2 k.

Тангенс угла пересечения интегральных кривых исходного уравнения с прямой y = kx определяется формулой Заметим, что исходное уравнение не изменится, если в нем заменить (x, y) на (x, y). Таким образом, интегральные кривые должны быть расположены симметрично относительно начала координат, поэтому достаточно построить их в правой полуплоскости (x 0). Если k = 0 или 1 то tg = 0 и, следовательно, лучи y = 0 и y = x (x 0) являются интегральными кривыми.

Исследуем поведение функции tg в зависимости от k. Прежде всего отметим, что tg 0 при k ±, а также при k 0 или 1. Таким образом, интегральные кривые входят в начало координат, касаясь одного из лучей y = 0, y = x или x = 0. Далее, знаменатель 2k 3 k 2 + 1 дроби (44) имеет один вещественный нуль k1 (1 k1 1/2). Если k k1, то tg и, следовательно, интегральные кривые данного уравнения, пересекают луч y = k1 x под углом в 90. Отметим, что tg 0 при С учетом полученной выше информации мы можем приближенно построить интегральные кривые исходного уравнения (см. рис. 18).

Задача 53. (135г*). Начертить приближенно интегральные кривые уравнения xy = y + y 2 + не решая его.

Решение. Данное уравнение определено в области + 1 0. Расx смотрим это уравнение при x 0, переписав его в виде В данном случае Поэтому (см. решение задачи 52), фазовые кривые пересекают луч y = kx, x 0 под углом, для которого Из этой формулы видно, что лучи y = 0 и y = x, x 0 (при k = 0 и k = 1) являются фазовыми кривыми исходного уравнения. Исследуя на промежутках (1, 0) и (0, +) нетрудно построить другие фазовые кривые данного уравнения (см. рис. 19).

и интегральные кривые пересекают луч y = kx, x 0 под углом,

48 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Лучи y = 0 и y = x (x 0) являются фазовыми кривыми исходного уравнения. Остальные фазовые кривые построим, исследуя функцию на промежутках (1, 0) и (0, +).

Отметим, что выражение, стоящее в знаменателе функции g(k), может обращаться в нуль при y = 0:

Исследуя функцию z = k 5 2k 2 1, легко установить, что уравнение = 0 имеет один положительный корень, k = k0. Следовательно, луч y = k0 x, x 0, пересекает фазовые кривые данного уравнения под прямым углом. Вычислив при необходимости значение функции g(k) еще в нескольких точках k (1, 0) (0, +), получим достаточную информацию для приближенного построения фазовых кривых исходного уравнения при x 0 (рис. 20) Поведение фазовых кривых на всей плоскости показано на рис. 21.

5.1. Уравнения вида y + a(x)y = b(x).

5. ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Определение 8. Уравнение называется линейным.

Чтобы решить его следует вначале решить соответствующее однородное уравнение Уравнение (46) является уравнением с разделяющимися переменными.

Его решения имеют вид y(x) = Ce a(x)dx. Решение уравнения (45) ищется в виде где C(x) — неизвестная дифференцируемая функция. Подставляя (47) в уравнение (45) находим функцию C(x).

Замечание 6. Некоторые уравнения становятся линейными, если поменять местами искомую функцию и независимую переменную.

Задача 54. (136). Решить уравнение xy 2y = 2×4.

50 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Решение. Рассмотрим однородное уравнение xy 2y = 0. Функция y 0 является решением этого уравнения. Остальные решения этого уравнения найдем, разделяя переменные =. Отсюда находим ln |y| = 2 ln |x| + C или y = Cx2. Решение исходного уравнения ищем в виде y = C(x)x2. Подставляя это выражение в исходное уравнение, получим где C–произвольная вещественная константа. Решения исходного уравнения имеют вид y(x) = (x2 + C)x2 = Cx2 + x4.

Задача 55. (138). Решить уравнение y + ytgx = 1/ cos x.

Решение. Рассмотрим однородное уравнение y + ytgx = 0, соответствующее данному неоднородному уравнению. Это уравнение с разделяющимися переменными. Его общее решение имеет вид y = C cos x.

Ищем общее решение исходного неоднородного уравнения в виде y = C(x) cos x, где C(x) — неизвестная функция от x. Подставляя это выражение в уравнение y + ytgx = 1/ cos x, получим где C — произвольная константа. Итак, общее решение неоднородного уравнения имеет вид y = (C + tgx) cos x = C cos x + sin x.

Задача 56. (146). Решить уравнение (2ey x)y = 1.

5. ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Решение. Данное уравнение является линейным, если рассматривать x как функцию от y:

(48) Рассмотрим соответствующее однородное уравнение x = x, общее решение которого имеет вид x = Cey. Общее решение неоднородного уравнения (48) будем искать в виде x = C(y)ey. Подставляя это выражение в уравнение (48), получим где C — произвольная константа. Поэтому общее решение уравнения (48) имеет вид x = (e + e2y )ey = Cey + ey.

С помощью замены переменных или дифференцирования привести уравнения в заданиях 57-59 к линейным и решить их.

Задача 57. (161). xdx = (x2 2y + 1)dy.

Решение. Положим t = x2, тогда данное уравнение примет следующий вид:

Если рассматривать t как функцию от y, то последнее уравнение является линейным. Соответствующее однородное уравнение t = 2t имеет общее решение t = Ce2y. Общее решение неоднородного уравнения будем искать в виде t = C(y)e2y. Подставляя это выражение в неоднородное уравнение, получим Таким образом, общее решение неоднородного уравнения имеет вид t = (C + 2ye2y )e2y = Ce2y + 2y и, следовательно, общее решение исходного уравнения есть x2 = Ce2y + 2y.

Задача 58. (163). x(ey y ) = 2.

Решение. Разделив обе части данного уравнения на ey, получим x(1 ey y ) = 2ey. В полученном уравнении сделаем подстановку z = ey, тогда получим x(1 + z ) = 2z. Очевидно, это уравнение является линейным. Общее решение соответствующего однородного уравнения xz = 2z имеет вид z = Cx2. Тогда общее решение неоднородного уравнения будем искать в виде z(x) = C(x)x2. Подставляя это выражение в неоднородное уравнение, получим

52 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Таким образом, общее решение неоднородного уравнения имеет вид z = x + Cx2 и, следовательно, x + Cx2 = ey является общим решением исходного уравнения.

Решение. Запишем данное уравнение следующим образом:

Продифференцируем обе части последнего уравнения по x, тогда получим Положим z(x) = y(t)dt, тогда z = y и, следовательно, z = 2 + z.

Последнее уравнение является линейным. Общее решение соответствующего однородного уравнения имеет вид z = Cex. Будем искать общее решение неоднородного уравнения в виде z = C(x)ex. Подставляя последнее выражение в неоднородное уравнение, получим И, следовательно, z = 2 + Cex является общим решением неоднородного уравнения. Так как z(0) = 0, то C = 2, поэтому Продифференцировав последнее равенство по x, получим y(x) = 2ex.

Легко убедиться, что функция y = 2ex удовлетворяет исходному уравнению.

5.2. Уравнения Бернулли.

Определение 9. Уравнение вида называется уравнением Бернулли.

Уравнение Бернулли приводится к линейному уравнению делением обеих частей его на y n и введением новой искомой функции z по формуле z = y 1n.

Замечание 7. При n 0 уравнение Бернулли имеет решение y = 0.

Задача 60. (151). Решить уравнение y + 2y = y 2 ex.

5. ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Решение. Это уравнение Бернулли (n = 2). Заметим, что y является решением этого уравнения. Для нахождения остальных решений данного уравнения, разделим обе части этого уравнения на y 2, тогда получим (49) Сделав в уравнении (49) замену z = y 1, z = y 2 y, мы получим (50) Общее решение однородного уравнения z + 2z = 0 имеет вид z = Ce2x. Общее решение неоднородного уравнения (50) будем искать в виде z = C(x)e2x, где C(x) — неизвестная функция от x. Подставляя это выражение в уравнение (50), получим где C — произвольная константа. Поэтому общее решение уравнения (50) имеет вид Задача 61. (159). Решить уравнение y x3 sin y = xy 2y.

Решение. Данное уравнение является уравнением Бернулли, если рассматривать x как функцию от y:

(51) Очевидно, x 0 является решением уравнения (51). Для нахождения остальных решений уравнения (51) разделим обе части этого уравнения на x3, тогда получим (52) Подстановкой z = x2 уравнение (52) приводится к следующему виду:

Общее решение однородного уравнения yz + z = 0 имеет вид z = Cy 1.

Будем искать решения уравнения (53) в виде z = C(y)y 1. Подставляя это выражение в уравнение (53), получим где C — произвольная константа. Таким образом, общее решение уравнеcos y Легко проверить, что исходное уравнение допускает также тривиальное решение y = 0.

54 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

5.3. Уравнения Риккати.

Определение 10. Уравнение вида называется уравнением Риккати.

Уравнение Риккати интегрируется в квадратурах лишь в исключительных случаях. Если известно одно частное решение y1 уравнения Риккати, то заменой y = y1 + z уравнение Риккати приводится к уравнению Бернулли и, следовательно, может быть решено в квадратурах.

В задачах 62 и 63 путем подбора найти частное решение, привести данные уравнения Риккати к уравнениям Бернулли и решить их.

Решение. Будем искать частное решение данного уравнения в виде y1 = k/x. Подставляя y1 в уравнение, получим k + k + k 2 = 4 и, следовательно, функция y1 = k/x является решением исходного уравнения при k = ±2. Таким образом, мы получили два решения данного уравнения: y = 2/x и y = 2/x. Замена y = 2/x + z приводит исходное уравнение к виду Заметим, что полученное уравнение допускает решение z 0. Для нахождения остальных решений поделим обе части этого уравнения на xz и получим Подстановка u = z 1, u = z 2 z приводит это уравнение к линейному уравнению xu + 5u + x = 0.

Общее решение соответствующего однородного уравнения имеет вид u = Cx5. Общее решение неоднородного уравнения будем искать в виде u = C(x)x5. Подставляя последнее выражение в неоднородное уравнение, получим и, следовательно, u(x) = x/4 + Cx5 является общим решением неоднородного уравнения. Если вернуться к переменным x, y, то получим общее решение исходного уравнения

5. ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Решение. Будем искать частное решение данного уравнения в виде y1 = eax. Подставляя это выражение в исходное уравнение, получим aeax + 2eax ex e2ax e2x + ex. Очевидно, последнее тождество выполняется, если a = 1 и, следовательно, y1 = ex является решением данного уравнения.

Замена y = ex +z приводит исходное уравнение к уравнению Бернулли Последнее уравнение можно решить путем разделения переменных Кроме найденных решений это уравнение допускает и тривиальное решение z 0. Тогда решениями исходного уравнения являются функции Задача 64. (172). Найти траектории, ортогональные к линиям семейства y 2 = Cex + x + 1.

Решение. Прежде всего, составим дифференциальное уравнение данного семейства линий, для чего продифференцируем обе части равенства y 2 = Cex +x+1 по переменной x: 2yy = Cex +1. Исключая из последних двух равенств константу C, получим (54) Дифференциальное уравнение ортогональных траекторий получается из уравнения (54) заменой y на, т.е.

Очевидно, y = 0 является решением уравнения (55). Для нахождения остальных решений уравнения (55) рассмотрим x как функцию от y, тогда уравнение (55) примет следующий вид Последнее уравнение является линейным. Общее решение соответствующего однородного уравнения имеет вид x = C |y|. Общее решение неоднородного уравнения будем искать в виде x = C(y) |y|. Подставляя это выражение в уравнение (56), получим

56 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Таким образом, общее решение уравнения (56) имеет вид Задача 65. (174). Найти кривые, у которых площадь треугольника ограниченного касательной, осью абсцисс и отрезком от начала координат до точки касания, есть величина постоянная, равная a2.

Решение. Пусть y = y(x) — уравнение искомой кривой, M (x, y) произвольная точка взятая на этой кривой, тогда площадь треугольника P BM (см. рис. 22) определяется по формуле SBM P = SBM N +SN M P следовательно, Рассматривая x как функцию от y, последнее уравнение может быть переписано в виде (57)

5. ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Это уравнение является линейным. Общее решение однородного уравнения y 2 x = xy имеет вид x = Cy 1. Общее решение неоднородного уравнения (57) будем искать в виде x = C(y)y 1. Подставляя это выражение в уравнение (57), получим Тогда общее решение неоднородного уравнения (57) имеет вид x = y(C + 2a2 ln y).

Замечание 8. На рис. 21 изображено одно из возможных расположений кривой y = y(x) и точки M на ней. Остальные случаи рассматриваются аналогично.

Задача 66. (178). Найти то решение уравнения y sin 2x = 2(y + cos x), которое остается ограниченным при x /2.

Решение. Прежде всего, найдем общее решение данного уравнения.

Заметим, что общее решение соответствующего однородного уравнения имеет вид y = Ctgx. Общее решение исходного неоднородного уравнения будем искать в виде y = C(x)tgx. Подставляя последнее выражение в неоднородное уравнение, получим И, следовательно, общее решение исходного уравнения имеет вид Из формулы (58) следует, что при C = 1 решения, задаваемые равенством (58), при x /2 неограничены. При C = 1 из (58) получаем y(x) =. Пользуясь правилом Лопиталя, легко подсчитать, что lim y(x) = 1. Тем самым показано, что искомым решением является x/ y(x) = tgx 1/cosx.

Задача 67. (179*). Пусть в уравнении xy + ay = f (x) имеем a = const 0, f (x) b при x 0. Показать, что все решения этого уравнения имеют один и тот же конечный предел при x 0. Найти этот предел.

Решение. Заметим, что общее решение однородного уравнения xy + ay = 0 имеет вид y = Cxa. Общее решение неоднородного уравнения будем искать в виде y = C(x)xa. Подставляя последнее выражение в

58 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

исходное уравнение, получим Тогда y(x) = xa (C + d ), где C — произвольная вещественная константа, является общим решением исходного уравнения. Исследуем поведение функций при x 0.

Логически возможны два случая:

обязательно f (x) 0), тогда из равенства (59) непосредственно следует, что y(x) 0 при x 0;

б) интеграл d расходится, тогда из равенства (59) получаем Первое слагаемое в правой части (60), очевидно, равно нулю, а второй предел легко вычисляется при помощи правила Лопиталя. Действительно, Задача 68. (182*). Показать, что только одно решение уравнения xy (2×2 + 1)y = x2 стремится к конечному пределу при x +, и найти этот предел. Выразить это решение через интеграл.

Решение. Найдем общее решение данного уравнения. Для этого заметим, что общее решение однородного уравнения имеет вид y = Cxex.

Общее решение неоднородного уравнения будем искать в виде y = C(x)x ex. Подставляя это выражение в неоднородное уравнение, получим Итак, общее решение исходного уравнения имеет вид Изучим поведение решений исходного уравнения при x +. Прежде всего, заметим, что интеграл при всех 1. Таким образом, для существования конечного предела у функции при x + необходимо, чтобы C + как xex +. Поэтому единственное решение, которое может иметь конечный предел, это решение, которое соответствует значению и, следовательно, Убедимся, что функция y(x), определенная равенством (62), действительно имеет конечный предел при x +, для чего воспользуемся правилом Лопиталя:

6. Уравнения в полных дифференциалах. Интегрирующий 6.1. Уравнения в полных дифференциалах.

Определение 11. Уравнение называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции U (x, y), т. е.

60 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Тогда уравнение (63) можно переписать в виде dU = 0, так что его общее решение имеет вид U (x, y) = C.

Предположим, что функции M и N определены и непрерывны в некоторой односвязной области G и имеют в ней непрерывные частные производные соответственно по y и по x. Тогда для того, чтобы уравнение (63) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество Если условие (64) выполняется, то для нахождения функции U воспользуемся равенствами Интегрируя первое из этих равенств по x, определим функцию U (x, y) с точностью до произвольной дифференцируемой функции:

где (y) — произвольная дифференцируемая функция переменной y, а (x, y) — первообразная функции M (x, y). Дифференцируя (66) по y, с учетом второго равенства из (65) получаем уравнение для определения функции (y):

В задачах 69-71 проверить, что данные уравнения являются уравнениями в полных дифференциалах, и решить их.

Задача 69. (186). 2xydx + (x2 y 2 )dy = 0.

Решение. Заметим, что в нашем случае И, следовательно, данного уравнения является полным дифференциалом некоторой функции U. Для определения функции U составим систему (67) Из первого уравнения системы (67) имеем U (x, y) = x2 y + (y).

Дифференцируя найденную функцию по y и подставляя ее во второе уравнение системы (67), получим и, следовательно, (y) = + C1. Поэтому Задача 70. (188). ey dx (2y + xey )dy = Решение. Так как то левая часть данного уравнения является полным дифференциалом некоторой функции U, которая определяется из следующей системы Из первого уравнения имеем U = ey x + (y). Подставляя U во второе уравнение, получим И, следовательно, (y) = y 2 + C1. Таким образом, общее решение исходного уравнения имеет вид ey x y 2 = C.

Решение. В этом случае y = 0 (например, y 0; аналогично рассматривается и случай y 0), G = <(x, y)| y 0>и И, следовательно, в односвязной области G, т.е. левая часть данного уравнения является полным дифференциалом некоторой функции U в области G.

62 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Для определения функции U рассмотрим систему Из первого уравнения имеем U = + x + (y). Подставляя U во второе уравнение рассматриваемой системы, получим Таким образом, (y) = +C1 и, следовательно, общее решение исходного уравнения имеет вид 2 + x + = C.

6.2. Интегрирующий множитель. В некоторых случаях, когда левая часть уравнения (63) не является полным дифференциалом, удается подобрать функцию µ(x, y), после умножения на которую уравнение (63) становится уравнением в полных дифференциалах. Такая функция µ(x, y) называется интегрирующим множителем.

Из определения интегрирующего множителя имеем или откуда Таким образом, для нахождения интегрирующего множителя мы получили уравнение в частных производных.

Отметим некоторые частные случаи, когда удается сравнительно легко найти решение уравнения (68), т.е. найти интегрирующий множитель.

1. Если уравнение (63) имеет интегрирующий множитель, зависящий только от x, т.е. µ(x, y) = µ(x), то из (68) получаем Для существования интегрирующего множителя µ = µ(x), необходимо и достаточно, чтобы правая часть (69) была функцией только от x. В таком случае ln µ найдется квадратурой.

уравнение (63) имеет интегрирующий множитель µ = µ(y), зависящий только от y, который находится из уравнения 3. Если уравнение (63) имеет интегрирующий множитель вида µ(x, y) = µ((x, y)), где (x, y) — известная функция, то Решить уравнения 72–81, найдя каким-либо способом интегрирующий множитель или сделав замену переменных.

Задача 72. (195). (x2 + y 2 + x)dx + ydx = 0.

Решение. Для данного уравнения M (x, y) = x2 + y 2 + x, N (x, y) = y Тогда и, следовательно, исходное уравнение допускает интегрирующий множитель µ, зависящий только от x. Для определения µ воспользуемся равенствами (69) и (70):

обе части исходного уравнения на e2x, получим уравнение (71) которое является уравнением в полных дифференциалах. Для решения уравнения (71) составим систему (72) Из второго уравнения системы (72) имеем U (x, y) = e + (x).

Подставляя найденное выражение в первое уравнение системы (72), получим

64 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

и, следовательно, (x) = e + C1. Таким образом, общее решение уравнения (71), а значит и исходного уравнения, имеет вид Задача 73. (197). ydy = (xdy + ydx) 1 + y 2.

Решение. Введем новые переменные u и v по следующему правилу:

тогда исходное уравнение может быть приведено к виду Уравнение (73) является уравнением с разделяющимися переменными.

Разделив в (73) переменные, получим и, следовательно, v + 1 = u + C. Возвращаясь к старым переменным x, y, получим общее решение исходного уравнения y 2 + 1 = xy + C.

Задача 74. (199). y 2 dx (xy + x3 )dy = 0.

Решение. В этом случае Поэтому исходное уравнение допускает интегрирующий множитель µ, зависящий только от переменной x. Для нахождения µ воспользуемся уравнением Умножив обе части исходного уравнения на x3, получим уравнение которое является уравнением в полных дифференциалах. Для его решения составим систему Из первого уравнения получаем U (x, y) = 2 + (y). Подставляя это выражение во второе уравнение, получим и, следовательно, (y) = y + C1. Таким образом, общее решение уравy нения (74), а значит и исходного уравнения, имеет вид 2 y = C или y 2 = x2 (C 2y).

Задача 75. (203). y(x + y)dx + (xy + 1)dy = 0.

Решение. M = y(x + y), N = xy + 1;

Поэтому исходное уравнение допускает интегрирующий множитель µ, зависящий только от переменной y. Для нахождения µ воспользуемся уравнением исходного уравнения на y 1, получим (x + y)dx + (x + 1/y)dy = 0.

Последнее уравнение является уравнением в полных дифференциалах.

Для решения этого уравнения рассмотрим систему Из первого уравнения находим U (x, y) = + yx + (y). Подставляя найденное выражение во второе уравнение, получим и, следовательно, (y) = ln |y| + C1. Поэтому общее решение исходного уравнения имеет вид +xy+ln |y| = C. Очевидно, y 0 также является решением исходного уравнения.

Задача 76. (206). ydx xdy = 2×3 tg dx.

Решение. Сделаем подстановку y = ux, dy = udx + xdu, тогда исходное уравнение примет вид uxdx x(udx + xdu) = 2×3 tgudx, x2 du = 2×3 tgudx.

Последнее уравнение является уравнением с разделяющимися переменy ными. Решая его, находим sin u = Cex или sin x = Cex.

66 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Задача 77. (209). x2 y(ydx + xdy) = 2ydx + xdy.

Решение. Введем новую функцию u = xy, тогда du = xdy + ydx и наше уравнение примет следующий вид:

Последнее уравнение есть уравнение Бернулли. Очевидно, x 0 является решением рассматриваемого уравнения. Для нахождения остальных решений этого уравнения, разделим обе его части на x2 (x = 0), тогда получим (75) Сделаем подстановку x1 = t, t = x2, которая сводит уравнение (75) к линейному уравнению Решениями однородного уравнения являются функции t = Cu. Общее решение уравнения (76) будем искать в виде t = C(u)u. Подставляя это выражение в уравнение (76), получим Таким образом, общее решение уравнения (76) имеет вид t = u( ln u + C). Возвращаясь к старым переменным, получим x2 y ln xyC = 1. Отметим, что кроме найденных выше решений исходное уравнение допускает также решение y = 0.

Задача 78. (211). (2×2 y 2 + y)dx + (x3 y x)dy = 0.

Решение. Заметим, что x = 0 и y = 0 являются решениями данного уравнения. Положим = x2 y тогда исходное уравнение преобразуется к виду 3dx+x(1)d = 0. Разделив переменные и интегрируя, получим 3 ln |x| + ln || = C. Возвращаясь к переменным x, y, будем иметь а также x = 0 и y = 0.

Задача 79. (215). x(ln y + 2 ln x 1)dy = 2ydx.

Решение. Перепишем данное уравнение следующим образом:

Разделим обе части полученного уравнения на xy (xy = 0), тогда получим ln y + 2 ln x = Cy.

7. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ РЕШЕНИЯ

Задача 80. (217). (2×3 y 2 y)dx + (2×2 y 3 x)dy = 0.

Решение. Перепишем данное уравнение следующим образом:

(77) Введем новые переменные u, v по следующему правилу Тогда уравнение (77) примет вид (78) Общее решение уравнения (78) есть v = 1/u + C или uv = 1 + Cu.

Возвращаясь к старым переменным, получим xy(x2 + y 2 ) = 1 + C · xy.

Кроме указанных решений, данное уравнение допускает также решения x = 0 и y = 0, которые мы потеряли при интегрировании уравнения (78).

Задача 81. (220). y 2 (ydx 2xdy) = x3 (xdy 2ydx).

Решение. Заметим, что x = 0 и y = 0 являются решениями данного уравнения. Для нахождения остальных решений сгруппируем члены уравнения так, чтобы можно было выделить полные дифференциалы:

Так как то исходное уравнение примет вид Разделив переменные и интегрируя, будем иметь u 3 + 4 · v 3 = C.

Возвращаясь к исходным переменным, получим x 7. Существование и единственность решения 1. Теорема существования решения уравнения с начальным условием

68 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ БРЕСТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра информатики и прикладной математики МЕТОДИЧЕСКИЕ УКАЗАНИЯ для выполнения контрольных работ №1 и №2 по курсу Основы информатики и вычислительной техники для студентов заочного факультета специальности 25.01.09 Маркетинг Брест 2002 УДК 681.3 Методические указания содержат варианты заданий, вопросы и пояснения к выполнению заданий контрольных работ №1 и №2 по курсу Основы. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Тихоокеанский государственный университет Институт экономики и управления Кафедра Экономической кибернетики Методические указания к выполнению контрольных, курсовых работ По дисциплине Базы данных Для специальности 080801.65 Прикладная информатика в экономике очной и заочной форм обучения Методические указания разработаны в соответствии с составом УМКД Методические указания. »

«Министерство образования Республики Беларусь Учреждение образования Белорусский государственный университет информатики и радиоэлектроники Кафедра химии ХИМИЯ УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ для студентов всех специальностей БГУИР заочной, вечерней и дистанционной форм обучения В 2-х частях Часть 2 Минск 2005 УДК 54 (075.8) ББК 24 я 73 Х 46 Рецензент: зав. кафедрой РЭС БГУИР, проф. Н.С. Образцов А в т о р ы: И.В. Боднарь, А.П. Молочко, Н.П. Соловей, А.А. Позняк Химия: Учеб.-метод. пособие для студ. »

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Амурский государственный университет Кафедра математического анализа и моделирования УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ ИНФОРМАТИКА Модуль: Численные методы и математическое моделирование Основной образовательной программы по специальности 010701.65 – Физика Благовещенск 2011 г. УМКД разработан канд. физ.-мат. наук, доцентом Масловской. »

«Новые учебные издания для высших учебных заведений, поступившие в библиотеку в 2011 году: 1. А25 АБ 11-2006, 11-4606, 11-4607 КХ 11-2005 Ф Аграрное право:учебник/ [С. А. Боголюбов и др.]; отв. ред.: М. И. Палладина, Н. Г. Жаворонкова; Моск. гос. юрид. акад..М.: Проспект, 2011. 428, [4] с.; 22 см. Авт. указаны на обороте тит. л.Библиогр. в примеч. 2. Б23 КХ 11-5866 Ф Банковское дело:[учебник]/ под ред. Е. Д. Жукова, Н. Д. Эриашвили. 4-е изд., перераб. и доп.М.: ЮНИТИ, 2011. 686, [1] с.; 22 см. »

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Амурский государственный университет Кафедра Физики УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА СТУДЕНТА (НИРС) Основной образовательной программы по специальности 010701.65 — Физика Благовещенск 2012 2 СОДЕРЖАНИЕ 1. Рабочая программа учебной дисциплины 4 2. Краткое изложение программного материала 12 3. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Н. И. Шанченко Информационный менеджмент Учебное пособие для студентов специальности 351400 Прикладная информатика (в экономике) Ульяновск 2006 УДК 65.012.45 (075) ББК 65.290-2я73 Ш 20 Рецензент доктор технических наук, профессор Е. М. Булыжев Утверждено редакционно-издательским советом университета в качестве учебного пособия Шанченко, Н. И. Ш 20 Информационный. »

«НОУ ВПО ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ (г. Пятигорск) НОУ ВПО ИнЭУ Кафедра Информатики и математики УТВЕРЖДАЮ Председатель УМС Щеглов Н.Г. _ (Протокол № от 2012г.) Информационно-аналитические системы Методические указания по выполнению контрольной работы для студентов специальности 080801.62 Прикладная информатика (в экономике) очной и заочной формы обучения Пятигорск, 2012 Составитель: ст. преподаватель Микеладзе Т.С. Рецензент: к.э.н. Коновцова М. М. Методические указания по дисциплине. »

«Министерство образования и науки Самарской области государственное бюджетное образовательное учреждение среднего профессионального образования Сызранский медико-гуманитарный колледж Электронный глоссарий Гуманитарно-технологический профиль Версия 2.13 Сызрань – 2013 г. 1. Общеобразовательные дисциплины Биология Каменский А.А., Пасечник В.В. Биология. Общая биология. 10 — 11кл 2005 — 368с География Курашева Е.М. Экономич. и соц. география мира. 10кл. (в сх. и табл.)_Курашева Е.М_2011 -224с. »

«Министерство образования и науки Российской Федерации НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ История и методология прикладной математики и информатики Методические указания к выполнению расчетно-графического задания для студентов V-го курса ФПМИ по направлению 010500 дневного отделения Новосибирск, 2011 Методические указания предназначены для студентов, выполняющих расчетно-графическое задание по курсу История и методология прикладной математики и информатики (направление. »

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ФА КУ ЛЬТ ЕТ ИНФО Р МАТ ИКИ В.П. Леонов ВВЕДЕНИЕ В ФИЗИКУ И ТЕХНОЛОГИЮ ЭЛЕМЕНТНОЙ БАЗЫ ЭВМ И КОМПЬЮТЕРОВ Томск – 2008 УДК 681.3(075.8)+621.38.032(075) Л 476 Леонов В.П. Введение в физику и технологию элементной Л 476 базы ЭВМ и компьютеров: Учебное пособие. – Томск: Изд-во НТЛ, 2008. – 264 с. ISBN 978-5-89503-390-6 В учебном пособии рассмотрены основные этапы развития физики и технологии. »

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра общей математики и информатики УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ НОВЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В УЧЕБНОМ ПРОЦЕССЕ основной образовательной программы по направлению подготовки 040200.625 – социология Благовещенск 2012 1 УМКД разработан канд. пед. наук, доцентом, Чалкиной Натальей. »

«УДК 004.45(075.8) ББК -18.2*32.973я73 МИНОБРНАУКИ РОССИИ О 60 ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СЕРВИСА (ФГБОУ ВПО ПВГУС) Рецензент Кафедра Информационный и электронный сервис к.т.н., доц. Жуков Г. П. ОПЕРАЦИОННЫЕ СИСТЕМЫ ЛАБОРАТОРНЫЙ ПРАКТИКУМ для студентов направления 230100. Информатика и вычислительная техника Операционные системы : лабораторный практикум / сост. О 60 А. А. Попов, А. »

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ САНКТ-ПЕТЕРБУРГСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ А. В. Орлов ВНЕШНЯЯ ПОЛИТИКА И МЕЖДУНАРОДНЫЕ ОТНОШЕНИЯ РОССИИ С СЕРЕДИНЫ XIX ВЕКА ДО 1918 ГОДА Учебное пособие Санкт-Петербург 2011 Орлов А. В. Внешняя политика и международные отношения России с середины XIX века до 1918 года: Учебно-методическое пособие по дисциплине Отечественная история. — СПб: НИУ ИТМО, 2012. — 264 с. Курс Внешняя. »

«НОУ ВПО ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ (г. Пятигорск) НОУ ВПО ИнЭУ Кафедра Информатики и математики УТВЕРЖДАЮ Председатель УМС Щеглов Н.Г. _ (Протокол №1 от 30 082011г.) МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ ДИСЦИПЛИНА СТАТИСТИЧЕСКИЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ для студентов специальности 080801 Прикладная информатика (в экономике) заочной формы обучения Пятигорск, 2011 Составитель: Коновцова Марина Михайловна, к.э.н., доцент кафедры Информатики и математики Рецензент: Казуб В.Т. »

«Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Ивановский государственный энергетический университет имени В.И.Ленина Кафедра программного обеспечения компьютерных систем Методические указания для студентов очных и заочных факультетов по выполнению лабораторных работ по курсу ИНФОРМАТИКА (семестр 1, часть 1) Иваново 2006 Составители: М.Л. СОЛОВЬЕВ, В.П. ЗУБКОВ Редактор: В.А. ГУСЕВ Методические указания к изучению дисциплины. »

«Кафедра “Математика и информатика” А.Л. Дзюбенко ВВЕДЕНИЕ В ИНТЕРНЕТ _ Методические указания по проведению лабораторных работ для студентов МИЭМП всех форм обучения МОСКВА 2007 1 PDF created with pdfFactory Pro trial version www.pdffactory.com Автор – кандидат техничеких наук, доцент А.Л. Дзюбенко Дзюбенко А.Л. Введение в интернет. Методические указания по проведению лабораторных работ. / Сост. А.Л. Дзюбенко – М.: МИЭМП, 2007. – 110 с. Методические указания по проведению лабораторных работ. »

«Министерство образования РФ Восточно-Сибирский государственный технологический университет ОСНОВЫ РАБОТЫ С КОМПЬЮТЕРОМ Методические указания и варианты заданий Под редакцией проф., д.т.н. В.В. Найханова Улан-Удэ, 2000 2 УДК 681.3.05(03) Основы работы с компьютером. Методические указания и варианты заданий. Предназначено для студентов изучающих информатику. Составители: В.В.Найханов, А.А.Габагуев и Ц.Ц. Цыдыпов. Рецензент: к.т.н., доц. Т.В. Аюшеев. © ВСГТУ, 2000 3 ОГЛАВЛЕНИЕ Введение 1. »

«Министерство образования и науки Российской Федерации ФГБОУ ВПО Тамбовский государственный технический университет Факультет Магистратура Н.В. Молоткова, Т.И. Лапина ИСТОРИЯ ПРЕДПРИНИМАТЕЛЬСТВА В ПОДГОТОВКЕ МАГИСТРОВ ТОРГОВОГО ДЕЛА И БИЗНЕС-ИНФОРМАТИКИ Утверждено Методическим советом ТГТУ в качестве учебно-методического пособия для студентов магистратуры, обучающихся по направлениям Торговое дело, Бизнес-информатика Тамбов 2013 Рецензент д.э.н., доц. С.П. Спиридонов История предпринимательства. »

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Тверской государственный университет УТВЕРЖДАЮ Руководитель ООП подготовки магистров 2012 г. Учебно-методический комплекс по дисциплине ТЕОРИЯ НЕКООПЕРАТИВНЫХ ИГР В ЭКОНОМИКЕ для студентов 1 курса магистратуры Направление подготовки 230700 – Прикладная информатика Программа специализированной подготовки магистров Прикладная информатика в аналитической. »

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

источники:

http://poisk-ru.ru/s11784t9.html

http://diss.seluk.ru/m-informatika/1025532-1-obiknovennie-differencialnie-uravneniya-rukovodstvo-resheniyu-zadach-moldavskiy-gosudarstvenniy-universitet-kafedra-differencial.php