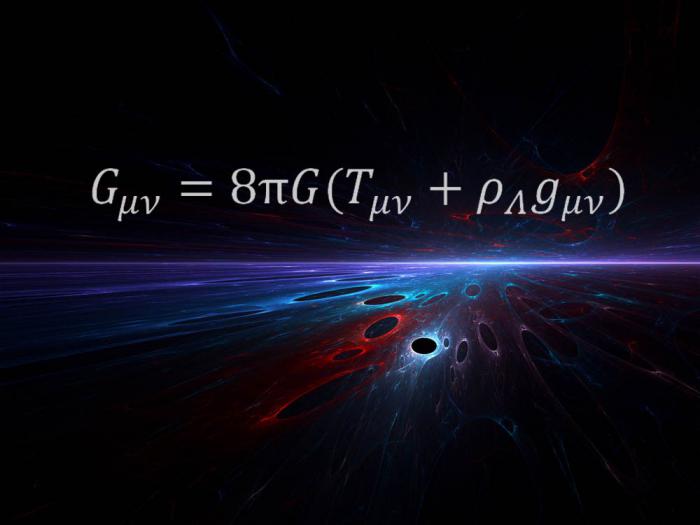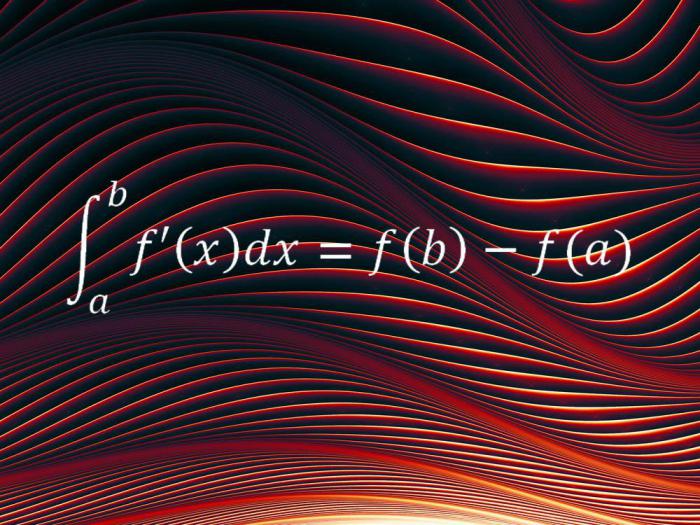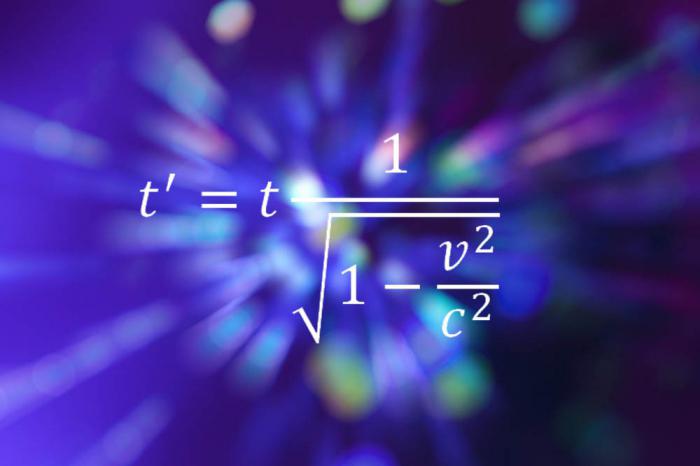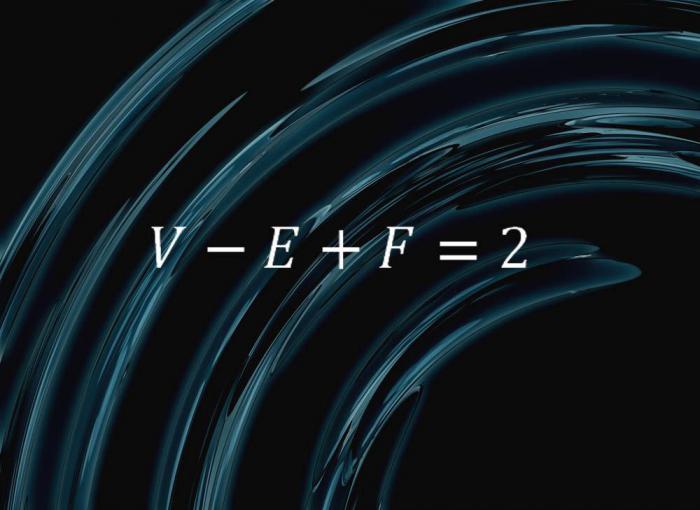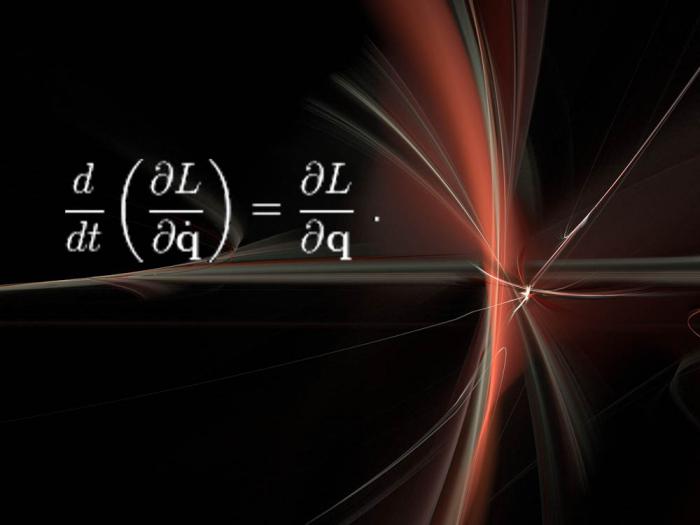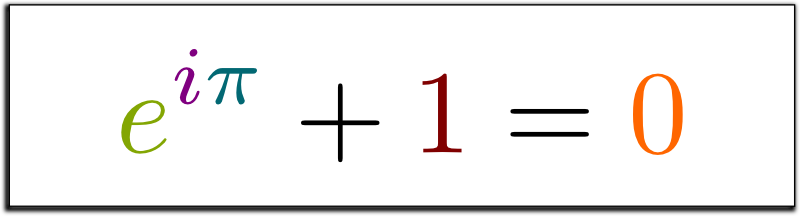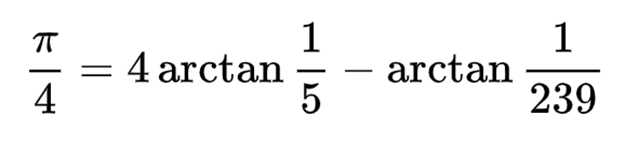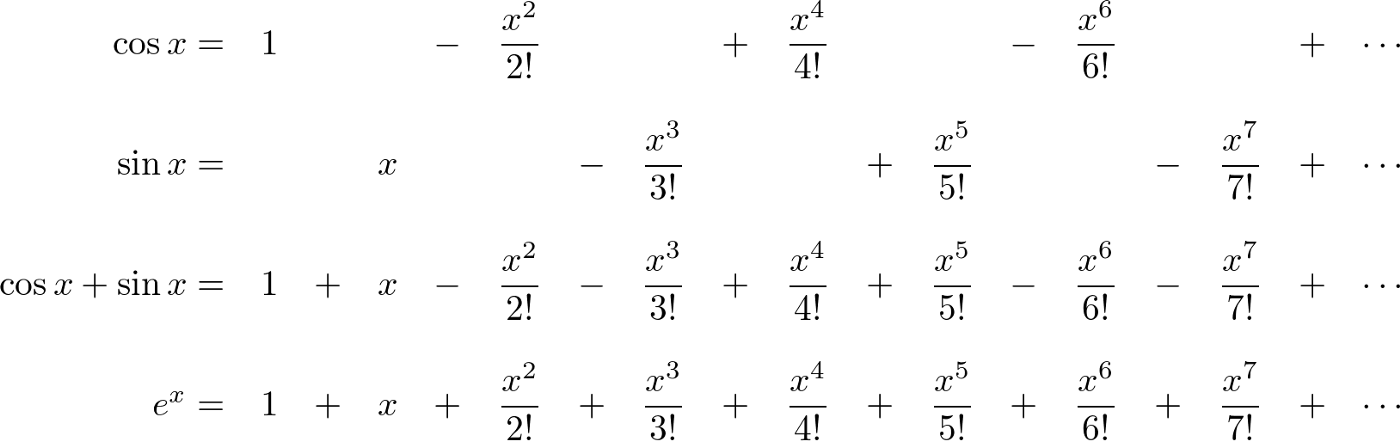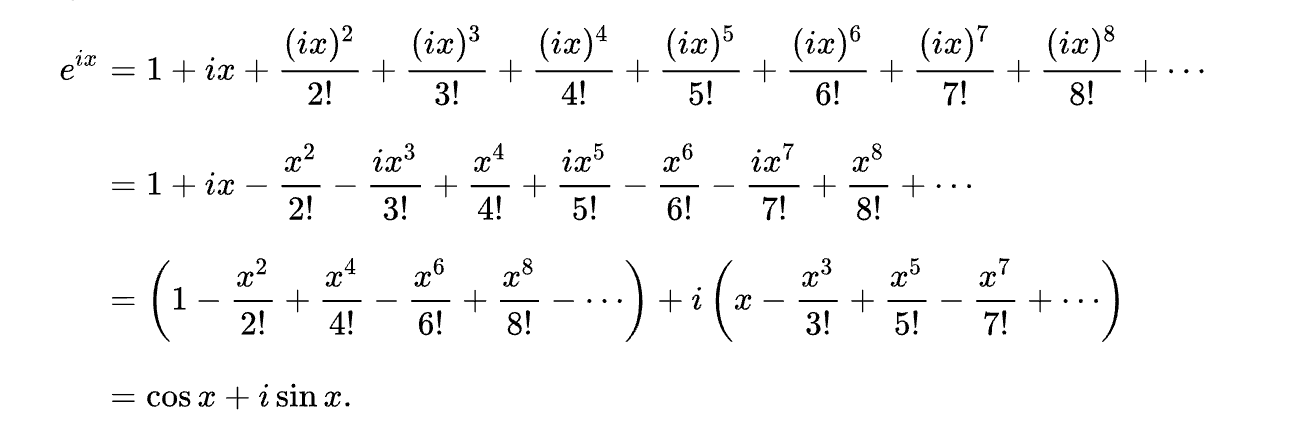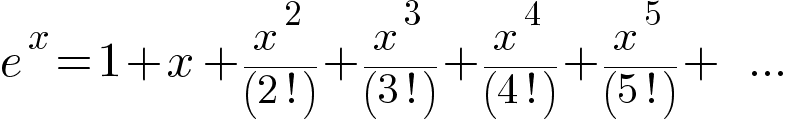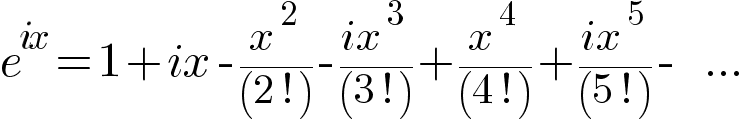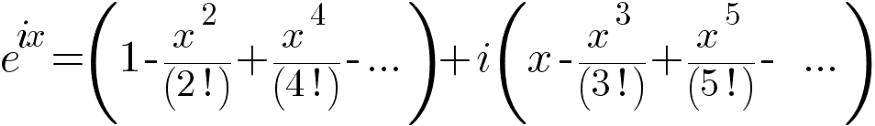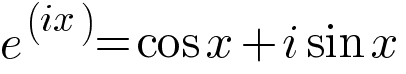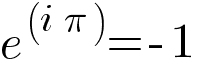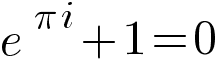Самое красивое уравнение в математике

Самые элегантные математические уравнения

Математические уравнения не только полезны – они также могут быть и красивы. И многие ученые признают, что они часто любят определенные формулы не только за их функциональность, но еще и за их форму, некую особую поэтичность. Есть те уравнения, которые известны на весь мир, как, например, E = mc^2. Другие не столь широко распространены, но красота уравнения не зависит от его популярности.

Общая теория относительности

Уравнение, описанное выше, было сформулировано Альбертом Эйнштейном в 1915 году как часть инновационной общей теории относительности. Теория на самом деле произвела революцию в мире науки. Это удивительно, как одним уравнением можно описать абсолютно все, что есть вокруг, в том числе пространство и время. Весь истинный гений Эйнштейна воплощен в нем. Это очень элегантное уравнение, которое кратко описывает, как все вокруг вас связано – например, как присутствие Солнца в галактике искривляет пространство и время так, чтобы Земля вращалась вокруг него.

Стандартная модель

Стандартная модель – это еще одна из важнейших теорий физики, в ней описываются все элементарные частицы, из которых состоит вселенная. Существуют различные уравнения, способные описать эту теорию, однако чаще всего пользуются уравнением Лагранжа, французского математика и астронома 18 века. Он успешно описал абсолютно все частицы и силы, которые на них воздействуют, за исключением гравитации. Это также включает недавно открытый бозон Хиггса. Оно в полной мере сочетается с квантовой механикой и общей теорией относительности.

Математический анализ

В то время как первые два уравнения описывают конкретные аспекты вселенной, данное уравнение может быть использовано во всех возможных ситуациях. Фундаментальная теорема математического анализа формирует основу математического метода, известного как исчисление, и связывает две свои основные идеи – концепцию интеграла и понятие производной. Зародился математический анализ еще в древности, однако все теории были собраны воедино Исааком Ньютоном в 17 веке – он использовал их для вычисления и описания движения планет вокруг Солнца.

Теорема Пифагора

Старым добрым известным всем уравнением выражается знаменитая теорема Пифагора, которую учат все школьники на уроках геометрии. Это формула описывает, что в любом прямоугольном треугольнике квадрат длины гипотенузы, самой длинной из всех сторон (c), равен сумме квадратов двух других сторон, катетов (a и b). В итоге, уравнение выглядит следующим образом: a^2 + b^2 = c^2. Эта теорема удивляет многих начинающих математиков и физиков, когда они только учатся в школе и еще не знают, что им готовит новый мир.

1 = 0.999999999….

Это простое уравнение указывает на то, что число 0.999 с бесконечным количеством девяток после запятой, на самом деле, равно единице. Это уравнение замечательно тем, что оно крайне простое, невероятно наглядное, но все же умудряется удивить и поразить многих. Некоторые люди не могут поверить в то, что это на самом деле так. Более того, красиво и само по себе уравнение – левая его часть представляет собой простейшую основу математики, а правая скрывает в себе тайны и загадки бесконечности.

Специальная теория относительности

Альберт Эйнштейн снова попадает в список, на этот раз со своей специальной теорией относительности, которая описывает, как время и пространство являются не абсолютными понятиями, а относительными – к скорости смотрящего. Это уравнение показывает, как время «расширяется», тем сильнее замедляясь, чем быстрее человек движется. На самом деле, уравнение не является таким уж сложным, простые производные, линейная алгебра. Однако то, что оно собой воплощает, представляет абсолютно новый способ смотреть на мир.

Уравнение Эйлера

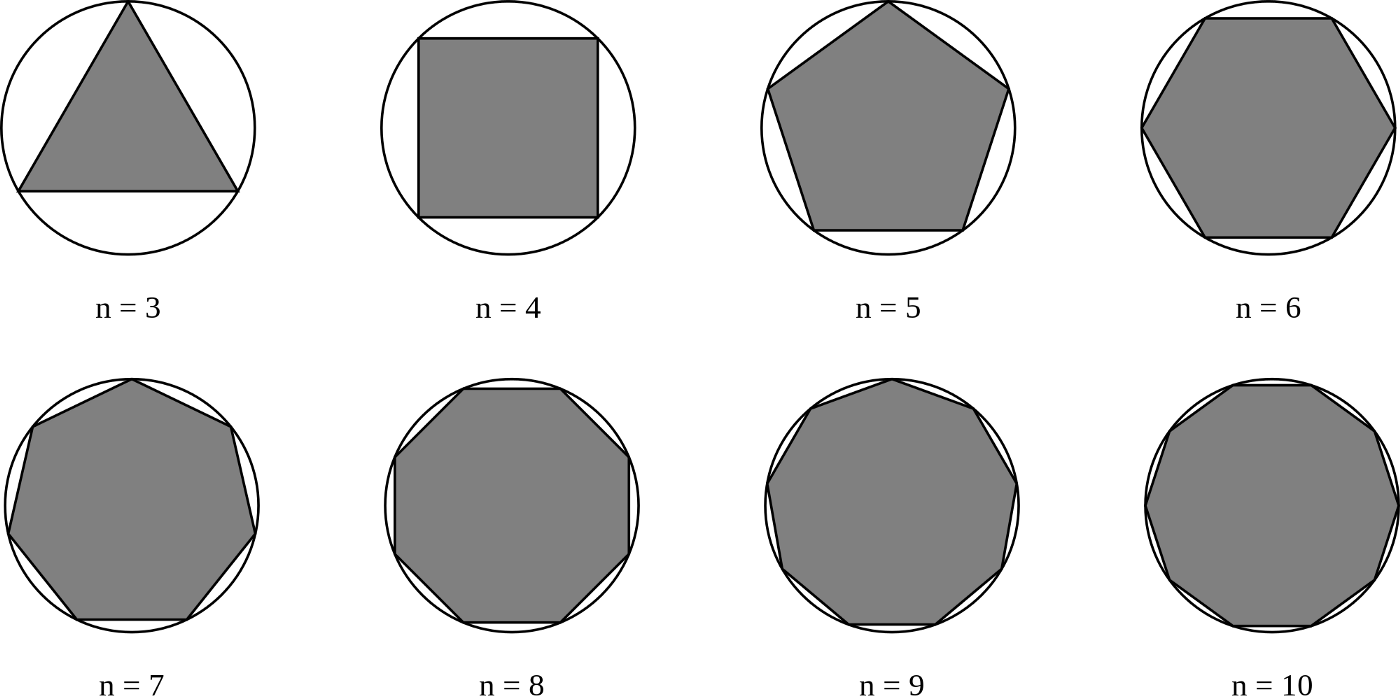
Эта простая формула включает в себя основные знания о природе сфер. Она говорит о том, что если вы разрезаете сферу и получаете грани, ребра и вершины, то если F принять за число граней, E — за число ребер, а V – за число вершин, то вы всегда получите одно и то же: V — E + F = 2. Именно так и выглядит данное уравнение. Поражает то, что какую бы сферическую форму вы ни взяли – будь-то тетраэдр, пирамида или любая другая комбинация граней, ребер и вершин, у вас всегда получится одинаковый результат. Эта комбинаторика рассказывает людям нечто фундаментальное о сферических формах.

Уравнение Эйлера-Лагранжа и теорема Нетер

Эти понятия являются довольно абстрактными, но очень сильными. Самое интересное заключается в том, что данный новый способ мышления о физике смог пережить несколько революций в данной науке, таких как открытие квантовой механики, теории относительности и так далее. Здесь L означает уравнение Лагранжа, которое является мерой энергии в физической системе. А решение этого уравнения расскажет вам о том, как конкретная система будет развиваться с течением времени. Вариантом уравнения Лагранжа является теорема Нетер, которая является фундаментальной для физики и роли симметрии. Суть теоремы заключается в том, что если ваша система симметрична, то в ней действует соответствующий закон сохранения. Собственно говоря, главная идея этой теоремы заключается в том, что законы физики действуют повсеместно.

Уравнение ренормгруппы

Это уравнение также называется по имени его создателей, уравнением Каллана-Симанчика. Оно является жизненно важным базовым уравнением, написанным в 1970 году. Оно служит для того, чтобы продемонстрировать, как наивные ожидания рушатся в квантовом мире. Уравнение также имеет множество приложений, позволяющих оценить массу и размер протона и нейтрона, которые составляют ядро атома.

Уравнение минимальной поверхности

Данное уравнение невероятным образом вычисляет и кодирует те самые красивые мыльные пленки, которые образуются на проволоке, когда ее окунают в мыльную воду. Данное уравнение, однако, сильно отличается от привычных линейных уравнений из той же области, например, уравнения тепла, образования волн и так далее. Это уравнение – нелинейно, оно включает в себя воздействие сторонних сил и производных продуктов.

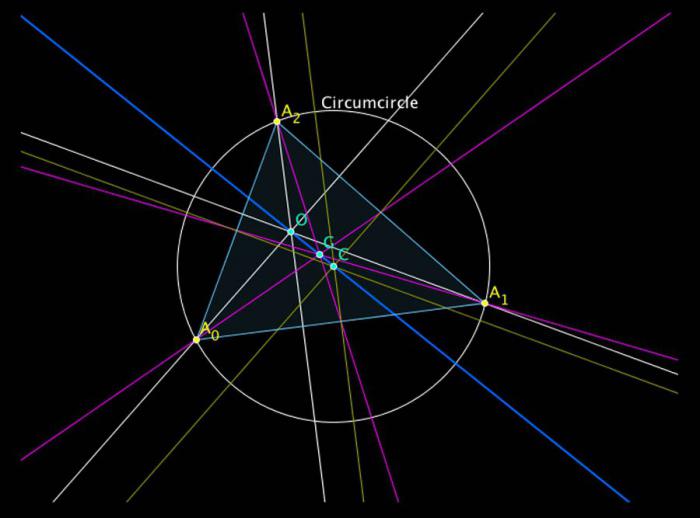
Прямая Эйлера

Возьмите любой треугольник, нарисуйте наименьший круг, который может включить в себя треугольник, и отыщите его центр. Найдите центр массы треугольника – ту точку, которая позволила бы треугольнику балансировать, например, на острие карандаша, если бы его можно было вырезать из бумаги. Нарисуйте три высоты этого треугольника (линии, которые были бы перпендикулярны тем сторонам треугольника, от которых они рисуются) и найдите точку их пересечения. Суть теоремы заключается в том, что все три точки будут находиться на одной прямой, именно это и есть прямая Эйлера. Теорема заключает в себе всю красоту и мощь математики, открывая удивительные закономерности в самых простых вещах.

Самая красивая теорема математики: тождество Эйлера

Посмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением. Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу.

Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».

Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.

Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».

Рисунок 2.0: обложка журнала The Mathematical Intelligencer

Рисунок 3.0: опрос Дэвида Уэллса из журнала

Леонарда Эйлера называют самым продуктивным математиком за всю историю. Других выдающихся математиков вдохновляли его работы. Один из лучших физиков в мире, Ричард Фейнман, в своих знаменитых лекциях по физике назвал уравнение Эйлера «самой примечательной формулой в математике». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу «…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой».

Существует множество интересных фактов об уравнении Эйлера. Например, оно встречалось в некоторых эпизодах «Симпсонов».

Рисунок 4.0: в этой сцене уравнение Эйлера можно заметить на второй книге в самой правой стопке.

Рисунок 5.0: в этой сцене уравнение Эйлера написано на футболке второстепенного персонажа.

Также уравнение Эйлера стало ключевым пунктом в уголовном деле. В 2003 году аспирант Калифорнийского технологического института Билли Коттрелл писал краской на чужих спортивных автомобилях уравнение Эйлера. На суде он сказал: «Я знал теорему Эйлера с пяти лет, и её обязаны знать все«.

Рисунок 6.0: марка, выпущенная в 1983 году в Германии в память о двухсотлетии со смерти Эйлера.

Рисунок 7.0: марка, выпущенная Швейцарией в 1957 году в честь 250-й годовщины Эйлера.

Почему уравнение Эйлера так важно?

Вы имеете полное право задаться вопросом: почему Билли Коттрелл считал, что об уравнении Эйлера обязаны знать все? И был настолько в этом уверен, что начал писать его на чужих машинах? Ответ прост: Эйлер воспользовался тремя фундаментальными константами математики и применил математические операции умножения и возведения в степень, чтобы записать красивую формулу, дающую в результате ноль или минус один.

• Константа e связана со степенными функциями.
• Константа i является не вещественным, а мнимым числом, равным квадратному корню из минус единицы.
• Знаменитая константа π (пи) связана с окружностями.

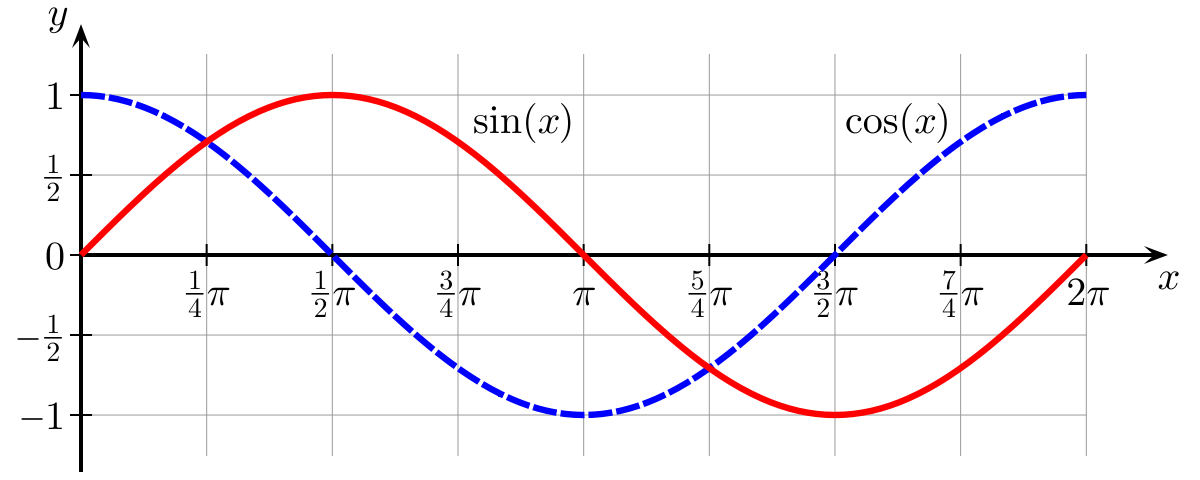
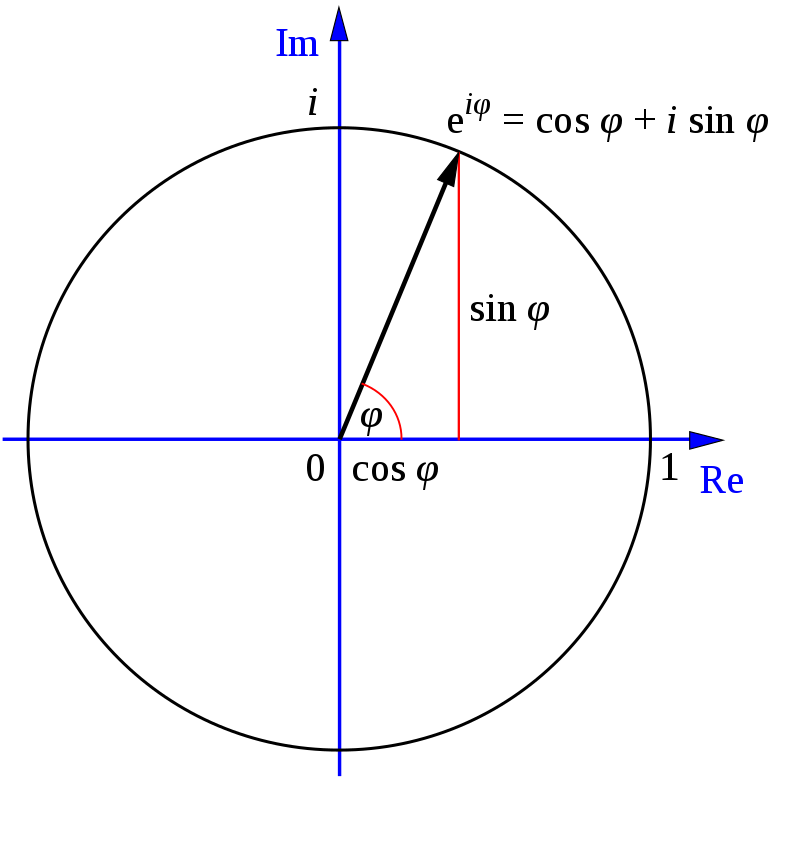
Впервые тождество Эйлера появилось в 1748 году в его книге Introductio in analysin infinitorum. Позже другие люди увидели, что эта формула связана с тригонометрическими функциями синуса и косинуса, и эта связь удивительна, ведь степенная функция стремится к бесконечности, а тригонометрические функции колеблются в интервале от — 1 до -1.

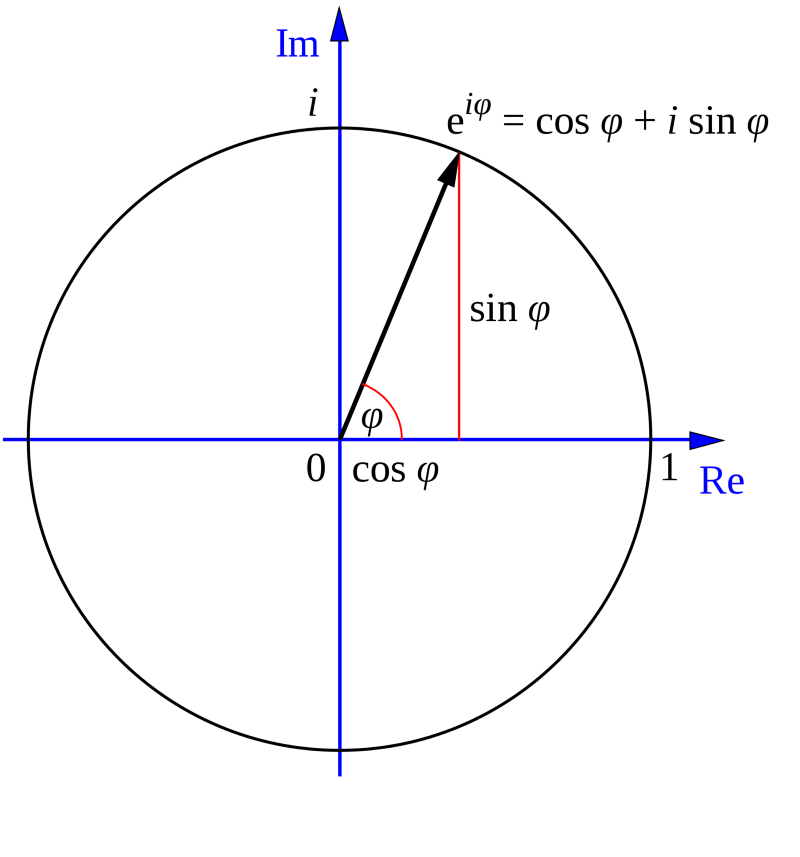
e в степени i, умноженного на ϕ (фи) = cos ϕ + i * sin ϕ

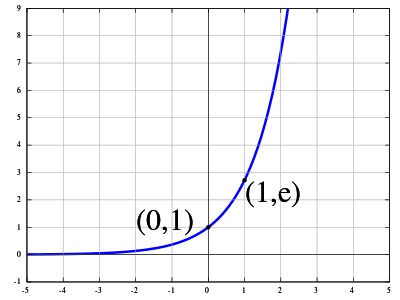
Рисунок 8.0: экспоненциальная функция y=e x .

Рисунок 8.1: график тождества Эйлера.

Рисунок 8.2: частоты, испускаемые LC-цепью.

Показанные выше уравнения и графы могут показаться абстрактными, но они важны для квантовой физики и вычислений обработки изображений, и при этом зависят от тождества Эйлера.

1: число для счёта

Число 1 (единица) является основой нашей системы исчисления. С неё мы начинаем счёт. Но как мы считаем? Чтобы считать, мы используем цифры 0–9 и систему разрядов, определяющую значение цифры.

Например, число 323 означает 3 сотни, 2 десятка и 3 единицы. Здесь число 3 исполняет две разные роли, которые зависят от его расположения.

323 = (3*100) + (2*10) + (3*1)

Существует и другая система исчисления, называемая двоичной. В этой системе вместо 10 используется основание 2. Она широко применяется в компьютерах и программировании. Например, в двоичной системе:

1001 = (2 3 ) + (0 2 ) + (0 1 ) + (2 0 ) = [9 в системе с основанием 10]

Кто создал системы исчисления? Как первые люди считали предметы или животных?

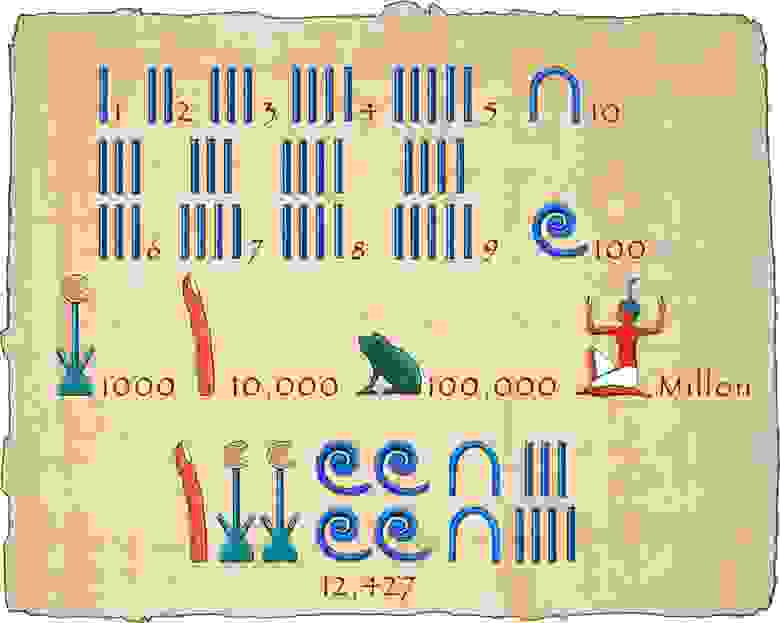
Как возникли наши системы исчисления? Как считали первые цивилизации? Мы точно знаем, что они не пользовались нашей разрядной системой. Например 4000 лет назад древние египтяне использовали систему исчисления с разными символами. Однако они комбинировали символы, создавая новый символ, обозначающий числа.

Рисунок 11: показанные здесь иероглифы образуют число 4622; это одно из чисел, вырезанных на стене в храме в Карнаке (Египет).

Рисунок 12: иероглифы — это изображения, обозначающие слова, а в данном случае — числа.

В то же время, но в другом месте ещё один социум обнаружил способ подсчёта, но в нём тоже использовались символы. Кроме того, основанием их системы исчисления было 60, а не 10. Мы используем их метод счёта для определения времени; поэтому в минуте 60 секунд, а в часе 60 минут.

Рисунок 13: вавилонские числа из шестидесятиричной системы счисления (с основанием 60).

Тысячу лет спустя древние римляне изобрели римские числа. Для обозначения чисел они использовали буквы. Римская нотация не считается разрядной системой, потому что для многих значений нашей системы счисления в ней использовались разные буквы. Именно по этой причине для счёта они использовали абакус.

Рисунок 14: романский абакус в шестнадцатеричной (с основанием 16) системе счисления

Рисунок 15: таблица преобразования из арабских в римские числа

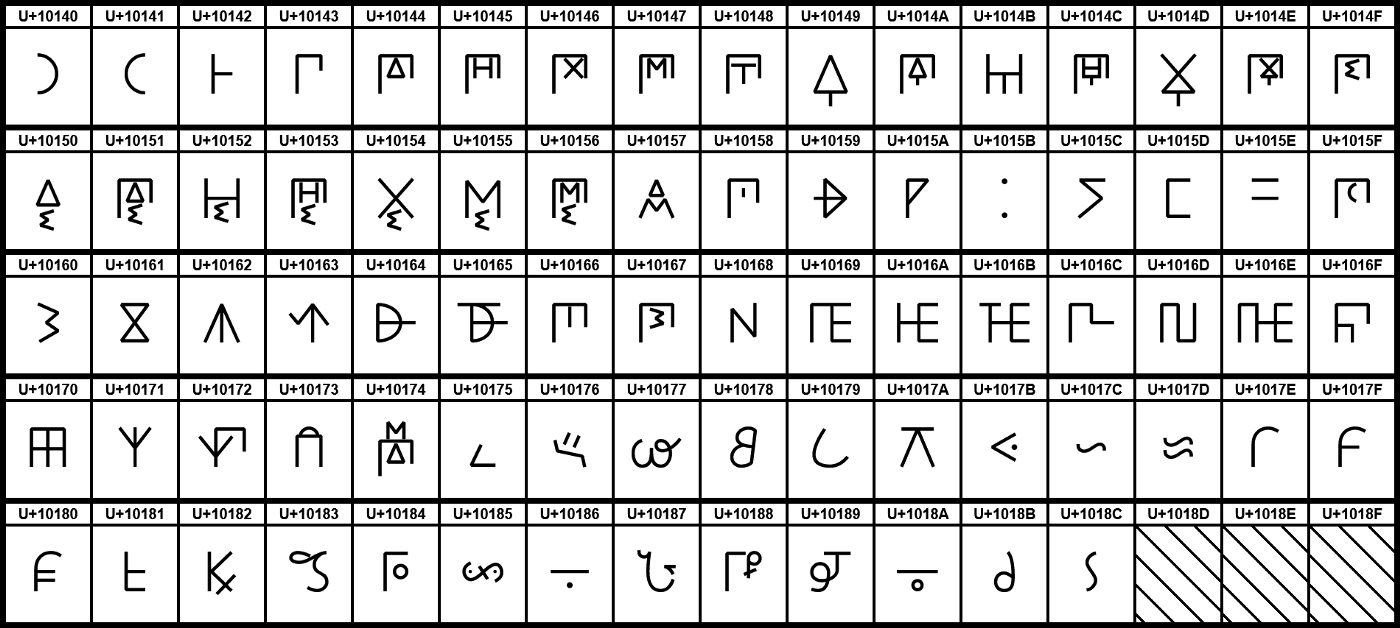
Древние греки тоже не использовали разрядную систему счисления. Греческие математики обозначали числа буквами. У них были специальные буквы для чисел от 100 до 900. Многие люди в то время считали греческие числа запутанными.

Рисунок 15: таблица букв древних греков.

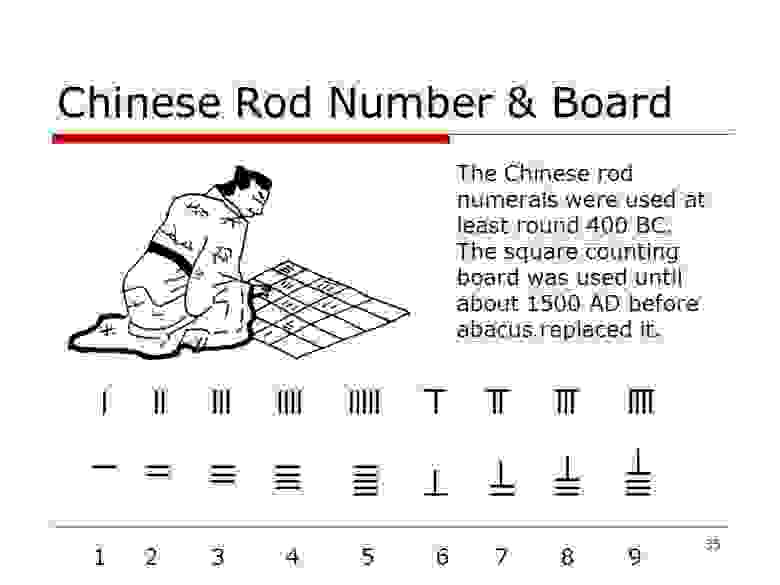
В то же самое время китайские математики начали использовать для расчётов небольшие бамбуковые палочки. Этот китайский способ счёта называют первой десятичной разрядной системой.

Рисунок 16: китайский способ счёта с числами-палочками. Использовался как минимум с 400 года до нашей эры. Квадратная счётная доска использовалась примерно до 1500 года, когда её заменил абакус.

Однако самая уникальная система счёта использовалась индейцами майя. Их система счисления имела основание 20. Для обозначения чисел от 1 до 19 они использовали точки и линии. Чем же отличалась их система счисления? Для каждого числа они использовали изображения голов и отдельный символ нуля 0.

Рисунок 17: Система счисления майя с основанием 20, в которой числа обозначались головами

Рисунок 18: ещё один способ записи чисел майя.

0: число для обозначения ничего

Некоторые цивилизации использовали пробелы, чтобы, например, отличать число 101 от 11. Спустя какое-то время начало появляться особое число — ноль. К примеру, в пещере в индийском городе Гвалиор археологи обнаружили на стене число 270, в котором был ноль. Самое первое зафиксированное использование нуля можно увидеть в Бодлианской библиотеке.

Рисунок 19: вырезанный на стене храма в Гвалиоре круг обозначает ноль. Ему примерно 1500 лет.

Рисунок 20: чёрные точки в манускрипте Бакхшали обозначают нули; это самый старый письменный пример использования числа, ему примерно 1800 лет.

Примерно 1400 лет назад были записаны правила вычислений с нулём. Например, при сложении отрицательного числа и нуля получается то же отрицательное число. Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.

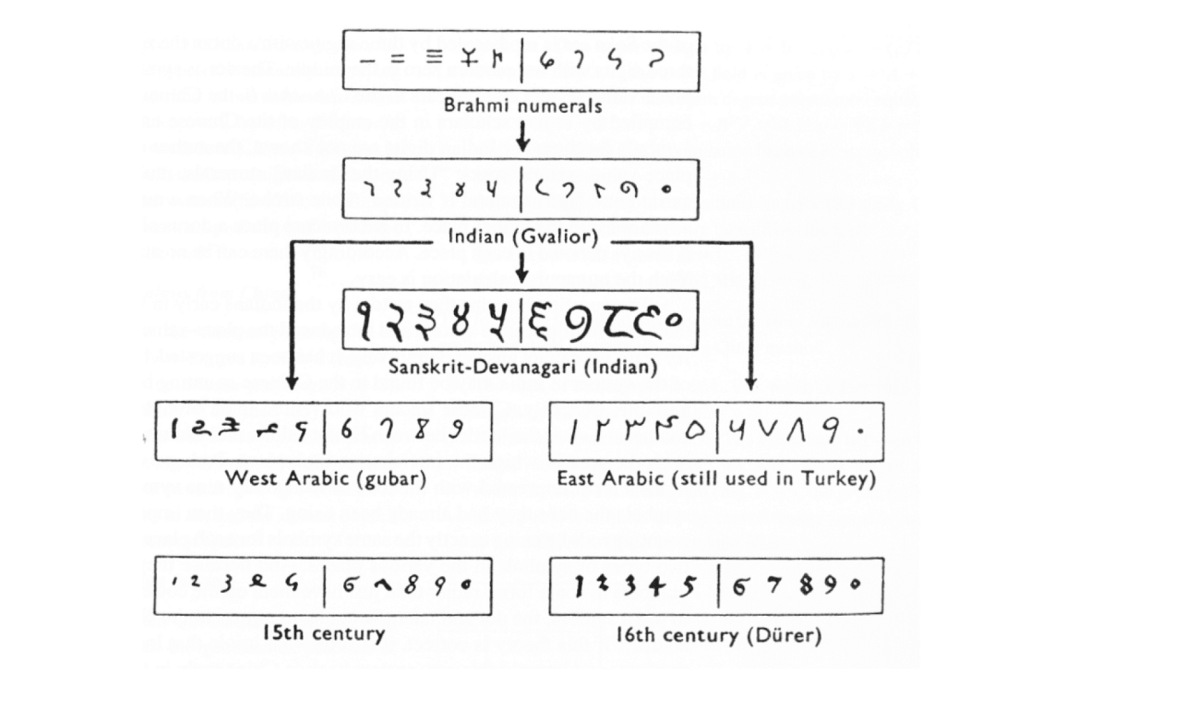
Вскоре после этого многими людьми были опубликованы книги по арифметике, распространяющие использование индо-арабской записи чисел. Ниже показана эволюция индо-арабских чисел. В большинстве стран используется индо-арабская система чисел, но арабские страны до сих пор пользуются арабскими числами.

Рисунок 21: на этой схеме показана эволюция чисел, происходящих от чисел брахми и заканчивающаяся числами, которыми мы используем и сегодня.

Рисунок 22: классическая гравюра «Арифметика» из Margarita Philosophica Грегора Рейша, на которой изображено соревнование между Боэцием, улыбающимся после открытия индо-арабских чисел и письменных вычислений, и нахмуренным Пифагором, до сих пор пытающимся пользоваться счётной доской.

Пи (π): самое известное иррациональное число

Пи — самое популярное из известных нам иррациональных чисел. Пи можно найти двумя способами: вычислив соотношение длины окружности к её диаметру, или соотношение площади круга к квадрату его радиуса. Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д.

π = окружность / диаметр ИЛИ π = площадь круга / радиус²

Рисунок 22: анимированная связь между окружностью и диаметром в отношении пи.

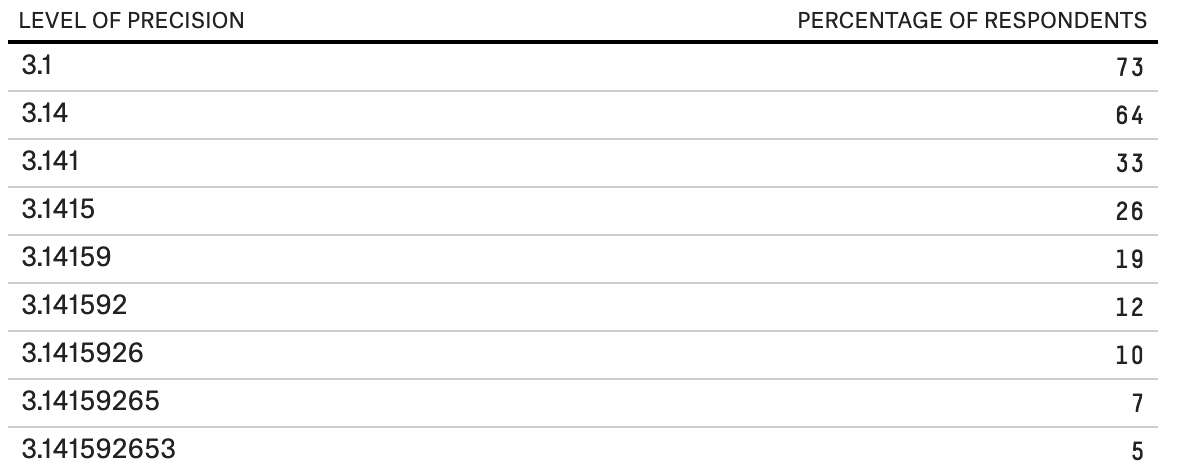
Так как иррациональные числа наподобие пи бесконечны и не имеют повторений, мы никогда не закончим записывать пи. Оно продолжается вечно. Есть люди, запомнившие множество десятичных разрядов пи (нынешний рекорд — 70 000 цифр! Источник: «Книга рекордов Гиннесса» ).

Рисунок 23: данные опроса 941 респондентов для определения процента людей, способных запомнить знаки пи после запятой.

Рисунок 24: На стене станции метро Karlsplatz в Вене записаны сотни разрядов пи.

На данный момент компьютеры смогли вычислить всего 2,7 триллиона разрядов пи. Может казаться, что это много, но на самом деле этот путь бесконечен.

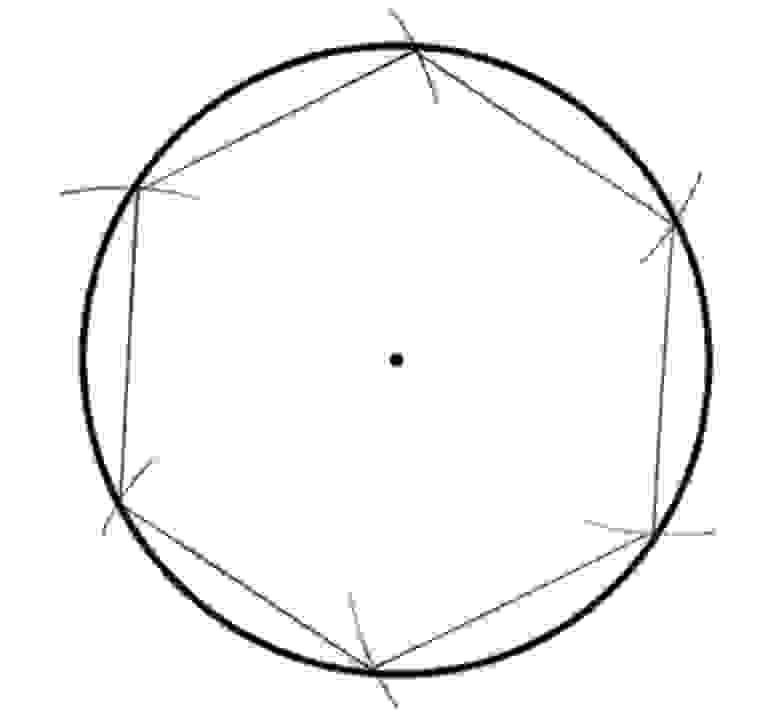
Как я сказал выше, число пи нашёл Евклид. Но как поступали люди до Евклида, когда им нужно было найти площадь круга? Историки обнаружили вавилонскую глиняную табличку, в которой было записано отношение периметра шестиугольника к диаметру описанной вокруг него окружности. После вычислений полученное число оказалось равным 3.125. Это очень близко к пи.

Рисунок 24: вавилонская глиняная табличка с отношением периметра шестиугольника к длине описанной окружности.

Древние египтяне тоже близко подобрались к значению пи. Историки обнаружили документ, показывающий, как древние египтяне нашли число пи. Когда историки перевели документ, то нашли такую задачу:

Например, чтобы найти площадь поля диаметром 9 хета (1 хет = 52,35 метра), нужно выполнить следующее вычисление:

Вычесть 1/9 диаметра, а именно 1. Остаток равен 8. Умножить его на 8, что даёт нам 64. Следовательно, площадь будет равна 64 setjat (единица измерения площади).

Другими словами, диаметр равен 2r, а 1/9 радиуса равно (1/9 • 2r). Тогда если мы вычтем это из исходного диаметра, то получим 2r — (1/9 • 2r) = 8/9(2r). Тогда площадь круга равна 256/81 r². То есть пи равно почти 3,16. Они обнаружили это значение пи примерно 4000 лет назад.

Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.

Спустя тысячу лет немецкий математик Людольф Цейлен работал со 2 62 -сторонним многоугольником и получил 35 десятичных разрядов пи. Это число, названное Людольфовым, было высечено на его могильном камне.

В 1706 году англичанин Джон Мэчин, долгое время работавший профессором астрономии, использовал формулу сложения, чтобы доказать, что пи равно

Не беспокоясь о том, как откуда взялась эта формула, Мэчин начал постоянно ею пользоваться, а затем записал показанный ниже ряд. Это был самый большой на то время шаг в количестве разрядов пи.

Однако первое упоминание пи появилось в 1706 году. Преподаватель математики Уильям Джонс написал книгу и впервые предложил пи для измерения окружностей. Так пи впервые появилась в книгах!

В 1873 году Уильям Шэнкс воспользовался формулой Джона Мэчина и получил 707 десятичных разрядов пи. Эти цифры написаны в комнате пи парижского Дворца открытий. Однако позже математики выяснили, что верными являются только 527 разрядов.

Рисунок 31: комната пи

С другой стороны, более интересный способ нахождения пи обнаружил Буффон. Его эксперимент основывался на случайном разбрасывании иголок для оценки пи. Он нарисовал на доске несколько параллельных линий на расстоянии D и взял иголки длиной L. Затем он случайным образом начал бросать иголки на доску и записывал долю иголок, пересекавших линию.

А после этого другой математик по имени Ладзарини подбросил иголку 3408 раз и получил шесть десятичных разрядов пи с соотношением 355/113. Однако если бы одна иголка не пересекла линию, он получил бы только 2 разряда пи.

Рисунок 32.1: бросание 1000 иголок для оценки приблизительного значения пи

e: история экспоненциального роста

e — это ещё одно знаменитое иррациональное число. Дробная часть e тоже бесконечна, как и у пи. Мы используем число e для вычисления степенного (экспоненциального) роста. Другими словами, мы используем e, когда видим очень быстрый рост или уменьшение.

Один из величайших, а возможно и лучший математик Леонард Эйлер открыл число e в 1736 году и впервые упомянул это особое число в своей книге Mechanica.

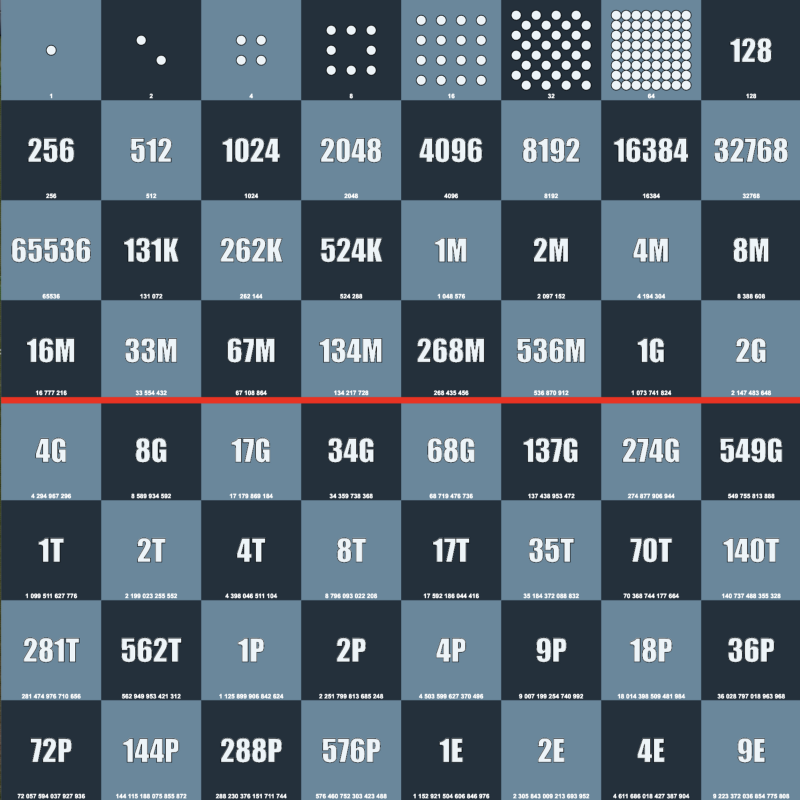
Чтобы разобраться в экспоненциальном росте, мы можем использовать историю об изобретателе шахмат. Когда он придумал эту игру, то показал её властителю Севера. Царю понравилась игра и он пообещал, что отдаст автору любую награду. Тогда изобретатель попросил нечто очень простое: 2 0 зерна на первую клетку шахматной доски, 2 1 зерна на вторую клетку доски, 2 2 зерна — на третью, и так далее. Каждый раз количество зерна удваивалось. Царь Севера подумал, что просьбу будет выполнить легко, но он ошибался, потому то на последнюю клетку нужно было бы положить 2 63 зёрен, что равно 9 223 372 036 854 775 808. Это и есть экспоненциальный рост. Он начался с 1, постоянно удваивался, и через 64 шага вырос в огромное число!

Если бы изобретатель шахмат выбрал линейное уравнение, например 2n, то получил бы 2, 4, 6, 8, … 128… Следовательно, в дальней перспективе экспоненциальный рост часто намного превышает полиномиальный.

Кстати, 9 223 372 036 854 775 808–1 — это максимальное значение 64-битного целого числа со знаком.

Число e открыл Эйлер. Однако Якоб Бернулли тоже работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег. Если вложить 100 долларов под 10% дохода, то как будет расти эта сумма? Во-первых, это зависит от того, как часто банк рассчитывает проценты. Например, если он рассчитывает один раз, то мы получим в конце года 110 долларов. Если мы передумаем и будем брать проценты каждые 6 месяцев, то в этом случае мы получим больше 110 долларов. Дело в ттом, что процент, полученный за первые 6 месяцев, тоже получит свой процент. Общая сумма будет равна 110,25 долларов. Можно догадаться, что мы можем получить больше денег, если будем забирать деньги каждый квартал года. А если мы будем делать временной интервал всё короче, то окончательные суммы будут продолжать расти. Такой бесконечный сложный процент сделает нас богатыми! Однако наш общий доход стремится к ограниченному значению, связанному с e.

Бернулли не называл число 2,71828 именем e. Когда Эйлер работал с 2,71828, он возвёл экспоненциальную функцию e в степень x. Свои открытия он изложил в книге The Analysis of Infinite.

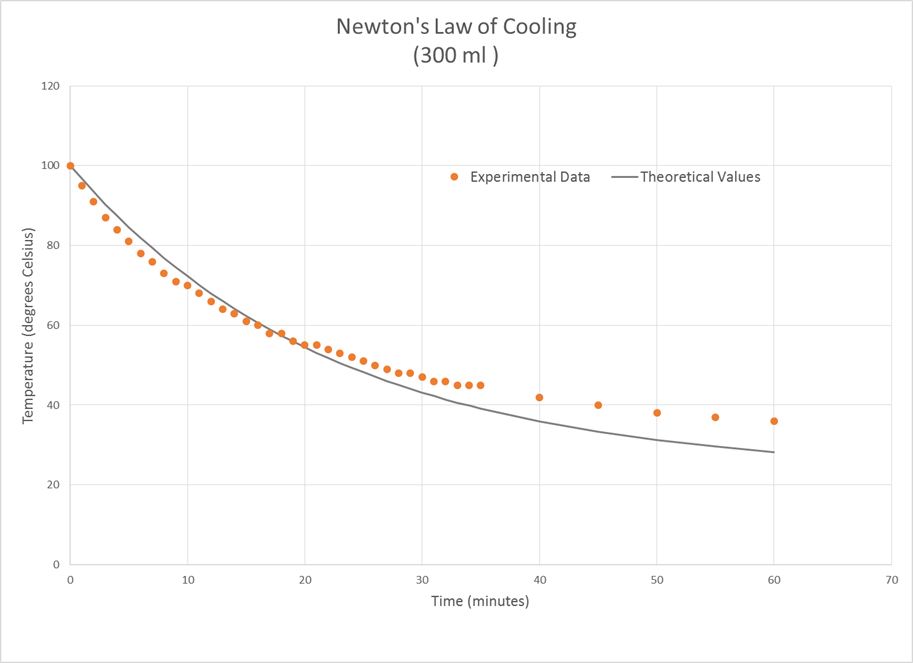
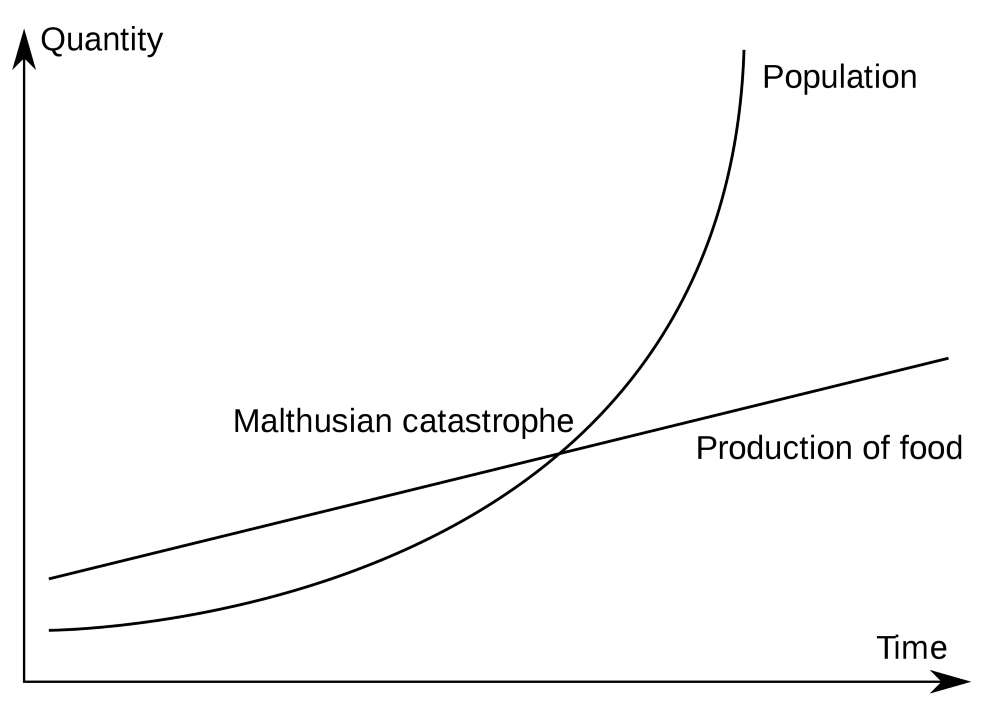
В 1798 году Томас Мальтус использовал экспоненциальную функцию в своём эссе, посвящённом пищевому дефициту будущего. Он создал линейный график, показывающий производство пищи и экспоненциальный график, показывающий население мира. Мальтус сделал вывод, что в дальней перспективе экспоненциальный рост победит, и мир ждёт серьёзный дефицит пищи. Это явление назвали «мальтузианской катастрофой». Ньютон тоже использовал эту модель, чтобы показать, как охлаждается чашка чая.

Рисунок 35: закон Ньютона-Рихмана

Рисунок 36: мальтузианская катастрофа

Мнимость числа: i, квадратный корень -1

Долгое время для решения своих задач математикам было достаточно обычных чисел. Однако в какой-то момент для дальнейшего развития им потребовалось открыть нечто новое и загадочное. Например, итальянский математик Кардано пытался разделить число 10 на 2 части, произведение которых было бы равно 40. Чтобы решить эту задачу, он записал уравнение: x (10-x) = 40. Когда он решил это квадратное уравнение, то получил два решения: 5 плюс √-15 и 5 минус √-15, что в то время не имело никакого смысла. Этот результат был бессмысленным, потому что по определению квадратного корня ему нужно было найти число, квадрат которого был бы отрицательным. Однако и положительное, и отрицательное числа в квадрате имеют положительное значение. Как бы то ни было, он нашёл своё уникальное число. Однако первым математиком, назвавшим √-1 (квадратный корень из минус единицы) мнимым числом i, был Эйлер.

Лейбниц дал такой комментарий о мнимом числе √-1:

Комплексные числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием.

Мы можем складывать, вычитать, умножать и делить мнимые числа. Сложение, вычитание и умножение просты, а деление немного сложнее. Вещественные и мнимые части складываются по отдельности. В случае умножения i 2 будет равно -1.

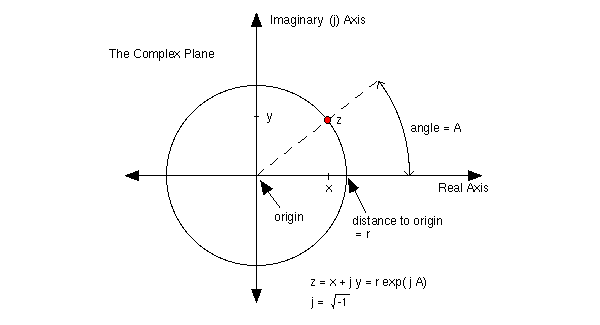
После Эйлера математик Каспар Вессель представил мнимые числа геометрически с создал комплексную плоскость. Сегодня мы представляем каждое комплексное число a + bi как точку с координатами (a,b).

Рисунки 37 и 38: комплексные числа

В викторианскую эпоху многие относились к мнимым числам с подозрением. Однако ирландский математик и астроном Уильям Роуэн Гамильтон покончил с этими сомнениями, определив комплексные числа применительно к кватернионам.

Самое красивое уравнение: тождество Эйлера

Тождество Эйлера связывает экспоненциальную функцию с функциями синуса и косинуса, значения которых колеблются от минус единицы до единицы. Чтобы найти связь с тригонометрическими функциями, мы можем представить их в виде бесконечного ряда, истинного для всех значений

Рисунок 40: тождество Эйлера

Эйлер никогда не записывал это тождество в явном виде, и мы не знаем, кто впервые записал его. Тем не менее, мы связываем его с именем Эйлера в знак почтения перед этим великим первопроходцем математики.

Тождество Эйлера — самое красивое математическое уравнение

Мы уже писали об удивительном свойстве числа e, которое может помочь, когда вслепую из конечного числа вариантов нужно выбрать единственный вариант. Сегодня давайте вспомним о тождестве Эйлера — по праву самом красивом уравнении, важное место в котором занимает число e, но не только оно. Представьте на секунду, что вы почти ничего не знаете о математике, только начинаете открывать её бесконечную красоту — и наслаждайтесь.

Все мы знаем о числе π — магическом отношении длины окружности к её диаметру. Число π можно приближённо представить в виде дроби 22/7. Особенность числа π состоит в том, что в его десятичной записи знаки после запятой никогда не заканчиваются. Его приближённое значение — 3,141592653589793238… Вот почему π называют иррациональным числом — его нельзя записать в виде конечного числа цифр после запятой. А вот другое интересное иррациональное число — e. Число e — это «число Эйлера» (от Euler). Вот первые несколько цифр числа e: 2,7182818284590…

Мало того, что это число иррациональное, оно применяется буквально во всех областях математики. Оно используется в логарифмических функциях как основание логарифма. Мы называем такой логарифм натуральным и записываем его так: ln x.

Что означает эта запись? В натуральном логарифме f(x)=ln(x) — это степень, в которую нужно возвести число e, чтобы получить x. Как же рассчитать значение e, спросите вы? Есть несколько способов.

Вот один из них: e — это предел последовательности, общий член которой равняется (1+ 1/n)ⁿ. Вот ещё один: площадь области под графиком y=1/x от x=1 до x=e равняется одному единичному квадрату.

Ещё один способ определения e: посмотрите на ряд 1 + 1/1! + 1/2! + 1/3! + 1/4! +…. Сумма этого ряда равняется e.

Чтобы вы почувствовали, насколько важным может быть число e, рассмотрим пример. Предположим, есть стеллаж с книгами, на каждой полке которого стоит только одна конкретная книга. Предположим также, что кто-то скинет на пол все книги и вы начнёте подбирать их с пола одну за одной и снова ставить на полки. Вероятность того, что каждая книга попадёт не на свою полку, составляет примерно 1/e. Чем больше книг, тем ближе такая вероятность будет к значению 1/e.

Поговорим теперь о другом интересном математическом объекте. Он называется просто: i. Разберёмся, что это такое.

Если умножить 2 на 2, получится 4. То есть 2 в квадрате равняется 4. Квадрат положительного числа — это положительное число. Но, если возвести в квадрат –2, также получится 4, то есть положительное число. Другими словами, ни один квадрат действительного числа не может быть отрицательным числом. Вот тут-то и возникает понятие мнимого числа.

Число √-1 записывается буквой i. i означает мнимую (imaginary) единицу. То есть запись √-5 можно заменить записью √5 i. Отсюда следует, что i² = -1. Число i формирует множество комплексных чисел, то есть комбинаций действительных и мнимых чисел. Например, запись 8 + i√5 является комплексным числом. Для визуализации комплексных чисел используется плоскость мнимых чисел.

Комплексные числа. Источник: Wikimedia Commons

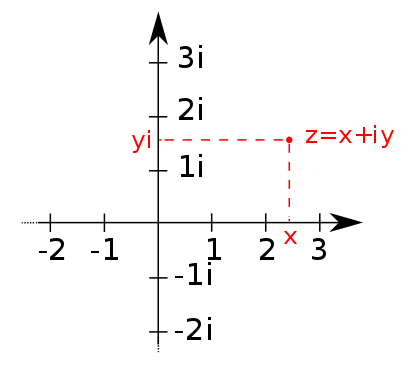
Изучать свойства комплексных чисел математики начали примерно с середины XVIII века. Однажды Эйлер развлекался с женой Тейлора… ох, простите… с рядом Тейлора. Ряд Тейлора:

Этому сумасброду просто стало интересно, как будет вести себя ряд Тейлора, если подставить в него число i (а что, вполне нормальная мысль для любого сумасброда).

И вот что у него начало получаться:

Но i² = -1 (Ух! Меня уже начинает охватывать научный азарт!) Сгруппируем все члены ряда, содержащие i.

Догадываетесь, что будет дальше? Одни члены ряда, содержащие i, сводятся в одну группу, а другие, не содержащие мнимую часть, то есть без числа i, — в другую. Получаются два ряда Тейлора: один — для косинуса, другой — для синуса.

Мы получили знаменитую формулу Эйлера. Различные значения x и e^(ix) можно отразить на комплексной плоскости. Например,

Это комплексное число, которое может быть представлено на комплексной плоскости. Если продолжить наносить на график точки e^(ix) для разных значений x, получится окружность.

Формула Эйлера. Источник: Wikimedia Commons

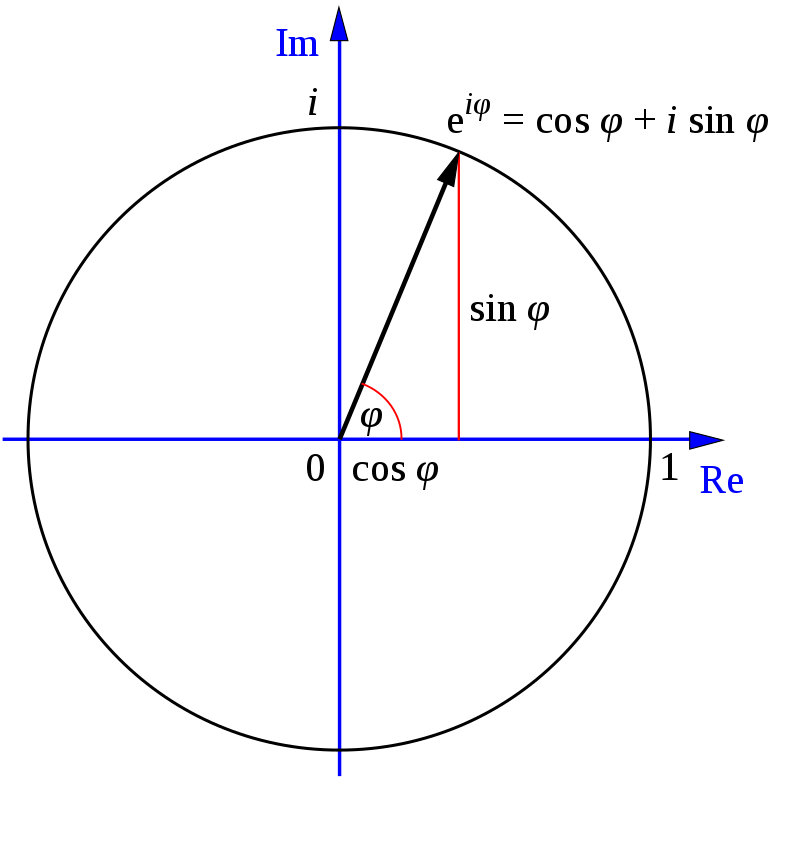
Если нужно узнать радиус r в любой точке (например, в точке 5 + 7i), рассчитывается значение x и берётся действительная часть re^(ix). Наконец, если в формулу Эйлера подставить значение x = π, получаем:

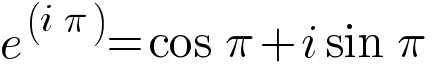
(поскольку cos π = −1 и sin π = 0).

Объединив три самых необыкновенных математических символа, получаем магическое уравнение:

Вот оно перед вами — по мнению математиков, самое красивое уравнение во всей математике. Оно называется Тождеством Эйлера.

Приходите на курс «математика для Data Science» — и наши менторы покажут, как при помощи математики менять мир к лучшему. Но даже если менять мир в ваши планы пока не входит — там можно будет подтянуть математическую базу. Будет сложно, но интересно.

Узнайте , как прокачаться и в других специальностях или освоить их с нуля: