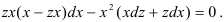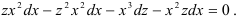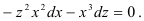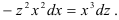Урок обобщения и систематизации знаний по теме «Дифференциальные уравнения»
Разделы: Математика
«Великая книга природы написана на языке математики»
Вид занятия: сдвоенный урок.
Тип занятия: урок обобщения и систематизации знаний.
Формы занятия: индивидуальная, групповая, фронтальная.
Продолжительность занятия: 90 мин.
Цель занятия: обобщить и систематизировать знания по теме «Дифференциальные уравнения», провести диагностику усвоения системы знаний и умений выполнять задания стандартного уровня.
Учебно-методическое обеспечение: тест, презентация преподавателя , задачи для индивидуального решения, уравнения для группового решения, задания для самостоятельной работы, лист оценки знаний студента .
Хронокарта занятия:
1. Оргмомент (5 мин).
2. Мотивационная беседа с последующей постановкой цели (5 мин).
3. Актуализация опорных знаний:
3.1. Тестирование (5 мин);
3.2. Фронтальный опрос (8 мин).
4. Систематизация умений решать задания стандартного уровня, повторение алгоритмов:
4.1. Коллективное решение задач, составление алгоритмов; (25 мин);
4.2. Разноуровневая самостоятельная работа. (20 мин).Приложение 2
5. Задачи прикладного характера:
5.1 историческая справка по применению дифференциальных уравнений (5 мин);
5.2 презентации (10 мин).
6. Домашнее задание (2 мин).
7. Рефлексия (5 мин).
1. Оргмомент
Студенты разделились на 6 групп. В каждой группе есть консультант – студент, который помогает ребятам своей группы, оценивает их работу.
Здравствуйте, студенты и гости, присутствующие на нашем занятии.
Цель нашего занятия: обобщить и систематизировать знания по теме «Дифференциальные уравнения». Для достижения этой цели мы проведем предварительное тестирование с самооценкой, чтобы увидеть свои пробелы в знаниях; фронтальный опрос по тем вопросам, которые были выданы для подготовки к занятию; групповое решение уравнений с проверкой на доске и создание алгоритмов решения каждого типа уравнения (поэтому мы разделились с вами на 6 групп). Увидим презентации задач прикладного характера, которые студенты подготовили дома.
И в заключение, выполним разноуровневую самостоятельную работу. Результаты оценивания знаний на разных этапах заносятся в лист оценки знаний каждого студента. В процессе занятия учитывается и индивидуальная, и групповая формы работы.
2. Мотивационная беседа с последующей постановкой цели
Теория дифференциальных уравнений является заключительной темой после изучения дифференциально–интегрального исчисления. Тема эта очень сложная. Она является важной для получения фундаментального естественно – научного образования. Для формирования представлений о математике, как о необходимой для каждого человека составляющей общих знаний о мире и понимания значимости этой науки для общественного прогресса
.
«Математика – это то, посредством чего люди управляют природой и собой», – писал А.Н.Колмогоров (выдающийся математик современности). Сегодня мы с вами должны обобщить и систематизировать материал по теме дифференциальных уравнений, совершенствовать свои умения и навыки, которые обязательно пригодятся, если мы продолжим потом свое обучение в высших учебных заведениях.
3. Актуализация опорных знаний
«Скажи мне – и я забуду.
Покажи мне – и я запомню.
Вовлеки меня – и я научусь»
3.1 Тестирование
Итак, каков смысл данного выражения? Чтобы овладеть знаниями и умениями мы информацию должны не только услышать и увидеть, но и вовлечь себя в работу. Я предлагаю для начала вам тест на 5 минут с самопроверкой, который оценивается по количеству правильных ответов. С его помощью мы проверяем свои знания.
Тест по теме «Дифференциальные уравнения»
1) Примеры дифференциальных уравнений:
2) Вид дифференциального уравнения у’ = х + 1:
а) линейное 1-го порядка;
б) однородное;
в) 2-го порядка с постоянными коэффициентами;
г) с разделяющимися переменными.
3) Решить задачу Коши – это найти
а) общее решение дифференциального уравнения;
б) начальные условия;
в) произвольную постоянную С;
г) частное решение дифференциального уравнения.
4) Решением дифференциального уравнения у» – 9 у = 0 является функция…
5) Разделение переменных в дифференциальном уравнении e x lnydx + xydy = 0 приведет его к виду…
а)

б)
в)
г)
1) Примеры дифференциальных уравнений 2-го порядка:
2) Вид дифференциального уравнения y’ + 4y – 2 = 0:
а) линейное 1-го порядка;
б) однородное;
в) 2-го порядка с постоянными коэффициентами;
г) с разделяющимися переменными.
3) Дифференциальное уравнение вида 
а) введения новой переменной y = z . x
б) разделения переменных
в) непосредственного интегрирования
г) введения новой переменной y = u . v
4) Решением дифференциального уравнения у» – 8y’ + 16у = 0 является функция…
5) Разделение переменных в дифференциальном уравнении приведет его к виду…
а)

б)
в)
г)
Проведем самопроверку теста. Сравните ответы, отметьте знаком + или – ответы. Оцените свою работу. Ответы на слайде .
Оценка: за 5 правильных ответов – «5», за 4 правильных ответа – «4», за 3 правильных ответа – «3», за 1, 2 правильных ответа – «2».
(Проверить результаты и выставить оценку в свой лист учета знаний)
3.2 Фронтальный опрос
А сейчас проведем фронтальный опрос по теории для того, чтобы частично подкорректировать знания тем, кто не совсем добросовестно повторял дома контрольные вопросы и имеет пробелы в знаниях.
- Какое уравнение называется дифференциальным? (Дифференциальным уравнением называется уравнение, содержащее производные или дифференциалы неизвестной функции).
- Как определить порядок ДУ? (Порядок ДУ определяется наивысшим порядком производной, содержащейся в этом уравнении).
- Какого порядка ДУ мы изучили? (Первого и второго порядка).
- Какие ДУ первого порядка вы знаете? (С разделяющимися переменными, однородные, линейные).
- Какие ДУ второго порядка мы изучили? (Сводящиеся к понижению степени и ОЛДУ 2-го порядка с постоянными коэффициентами).
- Составить схему классификации ДУ на доске с помощью магнитов и названий ДУ, написанных на плакатах. (Проверяется с помощью соответствующего слайда презентации)
- Может ли ЛДУ быть одновременно ЛДУ с разделяющимися переменным? Как решать такое уравнение? (Да. Решается как ЛДУ с разделяющимися переменными).
- Какие методы решения ЛДУ 1-го порядка вы знаете? (Метод Бернулли и метод вариации произвольной постоянной).
4. Систематизация умений решать задания стандартного уровня. Повторение алгоритмов.
Для проверки своих сил в решении конкретных уравнений я предлагаю каждой группе по одному или два уравнения на 10 минут. Решаем вместе, обмениваемся опытом. Когда группа справится с заданием, представитель выходит к доске и демонстрирует свои основные выкладки. После чего, мы еще раз сформулируем алгоритм решения каждого типа уравнения.
Итак, задание: определить вид уравнения, решить его, сформулировать алгоритм решения такого типа уравнения.
Алгоритмы
За участие в групповом решении консультанты должны выставить каждому оценку в лист учета знаний.
После такого повторения предлагается выполнить каждому студенту индивидуальную разноуровневую самостоятельную работу. Порядковый номер каждого задания дает количество набираемых баллов. Каждый выбирает задания для себя самостоятельно.
Самостоятельная работа (разноуровневая)
1) Определить вид дифференциального уравнения:
2) Составить характеристическое уравнение:
3) Зная и , записать общее решение дифференциального уравнения 2 порядка с постоянными коэффициентами:
4) Решить задачу Коши, если:
Если сумма баллов порядковых номеров решаемых примеров находится в пределах:
от 4 до 9 ,то оценка «3»;
от 10 до 15, то оценка «4»;
от 16 и выше, то оценка «5».
5. Задачи прикладного характера
«Три пути ведут к знанию:
Путь размышления – это путь самый благородный,
Путь подражания – это путь самый легкий
И путь опыта – это путь самый горький»
5.1. Историческая справка по применению дифференциальных уравнений
При изучении тех или иных физических, биологических процессов, механических явлений, ученым удается составить дифференциальные уравнения этого процесса или явления. А затем, решая это уравнение, удается вывести функциональный закон описания изучаемого вопроса. Дифференциальные уравнения играют большую роль в деле изучения природы и различных физических, химических и других процессов.
Существует много процессов в природе, которые описываются дифференциальными уравнениями. Например, процесс размножения бактерий, явление органического роста, изменение давления при подъеме над уровнем моря, ток самоиндукции, протекающий в катушке после выключения постоянного напряжения.
Можно так же написать дифференциальные уравнение движения планеты вокруг Солнца, искусственного спутника вокруг земли. Решая дифференциальные уравнения движения планет и их спутников (эти уравнения весьма сложны, т.к. планеты притягиваются не только к Солнцу, но и друг к другу), ученые предсказывают их будущее движение, узнают моменты солнечного и лунного затмений. Когда однажды оказалось, что планета Уран отклоняется от заранее вычисленной орбиты, ученые нисколько не сомневались в «правильности» математики. В середине 19 века французский астроном Леверье и английский астроном Джон Адамс одновременно и независимо один от другого сделали смелое предположение, что отклонение Урана вызывается притяжением к нему новой, до сих пор неизвестной планеты. С помощью дифференциальных уравнений они вычислили положение этой новой планеты и указали, где нужно искать на небе. Точно в указанном месте эта планета / её назвали НЕПТУН / была затем обнаружена. О ней говорят, что она открыта « на кончике пера» / путем вычислений/.
Тот факт, что самые различные явления описываются одинаковыми дифференциальными уравнениями, часто используется на практике.
5.2. Презентации
А сейчас мы посмотрим домашние презентации решения ряда прикладных задач.
Задачи:
- Найти кривую, проходящую через точку (2;3) и обладающую тем свойством, что отрезок любой её касательной, заключенный между координатными осями, делится пополам в точке касания.
- В теории резания возникает следующая задача: найти кривую, касательная к которой в каждой точке образует постоянный угол с радиусом вектором этой точки.
Демонстрация презентаций и пояснение к работе выполняются студентами ,
6. Домашнее задание:
Задача: Ускорение «a» материальной точки, движущейся прямолинейно в зависимости от времени «t», выражается формулой a=2t+3. Найти закон движения, если v=0, s=0 при t=0.
7. Рефлексия
Давайте подведем итог нашему занятию. Какие разделы математики мы сегодня с вами повторяли? (Степени и корни, логарифмы, функции и графики, тригонометрию, комплексные числа). Какие межпредметные связи были использованы? (Литература, физика, техническая механика). Таким образом, мы видим, что в теории дифференциальных уравнений математика, прежде всего, выступает как неотъемлемая часть естествознания, на которой основывается вывод и понимание количественных и качественных закономерностей, составляющих содержание наук о природе. Второй особенностью теории ДУ является ее связь с другими разделами математики. Она как бы находится на перекрестке математических дорог. Некоторые большие и важные разделы математики были вызваны к жизни задачами теории ДУ. Классическим примером такого взаимодействия являются исследования колебаний струны, проводившиеся в середине 18 века.
А что вы мне скажите по поводу нашего урока?
«Мы в такие ходили дали,
Что не очень-то и дойдешь.
Математику изучали,
Не взирая на снег и дождь.
Математика – вот наука,
Развивает она умы.
Не страшна никакая скука –
Коль задачи все решены!»
8. Подведение итогов: самооценка
Литература:
- Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика: Учебное пособие: В 2 кн. – М.: ООО «Издательство Новая волна», 2004.
- Б.В. Соболь, Н.Т. Мишняков, В.М. Поркшеян «Практикум по высшей математике». – Ростов-на-Дону, Феникс, 2004.
- Н.В. Богомолов. Практические занятия по математике. – Москва, Высшая школа, 1990.
Дифференциальные уравнения (варианты)
Это уравнение вида 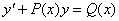


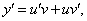
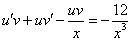
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 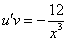
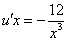
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Используем условие 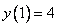

Ответ:
Решим соответствующее однородное уравнение
Составим характеристическое уравнение 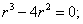
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид 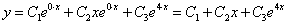
Частное решение неоднородного уравнения будем искать в виде 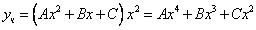
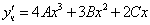
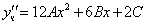
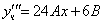
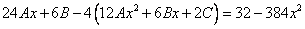
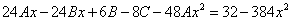
Тогда частное решение
Общее решение неоднородного примет вид:
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 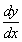
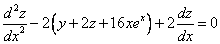
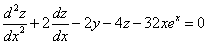
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение 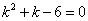
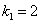
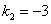
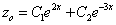
Частное решение неоднородного уравнения будем искать в виде 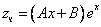

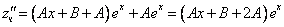
Подставим в исходное 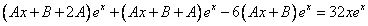
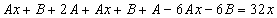
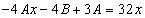
Тогда частное решение
Общее решение неоднородного примет вид:
Из второго уравнения
Ответ:
Вариант 2
Данное уравнение – уравнение с разделяющимися переменными. Разделим переменные: 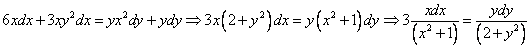
Посчитаем интегралы отдельно:
Тогда: 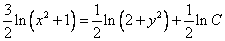
Ответ:
Это уравнение вида 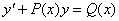


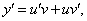
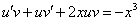
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 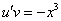
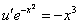
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
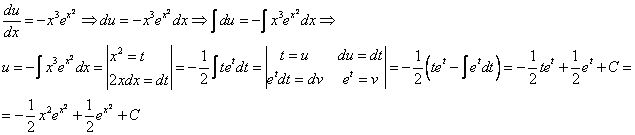
Используем условие 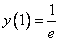
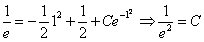
Ответ:
Данное уравнение не содержит у, следовательно понизить его порядок можно с помощью подстановки 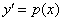
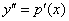
Отсюда 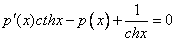
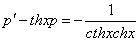
Замена 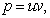
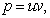
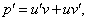
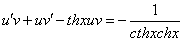
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 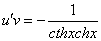
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Ответ:
Решим соответствующее однородное уравнение
Составим характеристическое уравнение 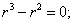
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид 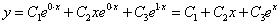
Частное решение неоднородного уравнения будем искать в виде 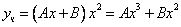

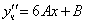
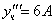
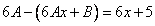
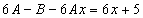
Тогда частное решение
Общее решение неоднородного примет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r3-3r2+4= 0
Корни характеристического уравнения:
R1 = -1 и корень характеристического уравнения r2 = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции: y1 = e-x, y2 = e2x, y3 = xe2x
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = (2•x-3)•e-x
Уравнение имеет частное решение вида:
Y’ =
Y» =
Y»’ =
которые подставляем в исходное дифференциальное уравнение:
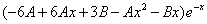
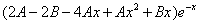
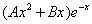
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Частное решение имеет вид:
Таким образом, общее решение дифференциального уравнения имеет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r3 — 16r = 0
Корни характеристического уравнения:r1 = -4, r2 = 0, r3 = 4
Следовательно, фундаментальную систему решений составляют функции:
Y1 = e-4x, y2 = e0x, y3 = e4x
Общее решение однородного уравнения имеет вид:
Правая часть F(x) = e2•x+3cos2x-sinx
Будем искать отдельно частные решения для F1(x) = e2•x, F2(x) = 3cos2x, F3(x) = — sinx
Рассмотрим правую часть: F1(x) = e2•x
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 1, Q(x) = 0, α = 2, β = 0.
Следовательно, число α + βi = 2 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (8•A•e2x) -16(2•A•e2x) = e2•x или -24•A•e2x = e2•x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = -1/24;
Частное решение имеет вид: y* = -1/24e2x
Рассмотрим правую часть: F2(x) = 3•cos(2•x)
Поиск частного решения.
Уравнение имеет частное решение вида:y* = Acos(2x) + Bsin(2x)
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (8•A•sin(2x)-8•B•cos(2x)) -16(2•B•cos(2x)-2•A•sin(2x)) = 3•cos(2•x)
или 40•A•sin(2x)-40•B•cos(2x) = 3•cos(2•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 0;B =-3/40;
Частное решение имеет вид:
Поиск частного решения.
Уравнение имеет частное решение вида: y* = Acos(x) + Bsin(x)
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (A•sin(x)-B•cos(x)) -16(B•cos(x)-A•sin(x)) = — sin(x)
или 17•A•sin(x)-17•B•cos(x) = — sin(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = -1/17;B = 0;
Частное решение имеет вид: y* = -1/17cos(x) + 0sin(x) или y* = -1/17cos(x)
Окончательно, общее решение данного уравнения
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 -6 r + 8 = 0
Корни характеристического уравнения: r1 = 2, r2 = 4
Следовательно, фундаментальную систему решений составляют функции: y1 = e4x, y2 = e2x
Общее решение однородного уравнения имеет вид:
Для поиска частного решения воспользуемся методом вариации произвольных постоянных. Для этого решим систему:
Тогда окончательно
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 -4 r + 4 = 0
Корни характеристического уравнения:
Корень характеристического уравнения r1 = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции: y1 = e2x, y2 = xe2x
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = e2•x•sin(5•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 1, Q(x) = 0, α = 2, β = 5.
Следовательно, число α + βi = 2 + 5i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y* = e2x(Acos(5x) + Bsin(5x))
Которые подставляем в исходное дифференциальное уравнение:
Y» -4y’ + 4y = (-e2x((20•A+21•B)•sin(5x)+(21•A-20•B)•cos(5x))) -4(e2x((2•B-5•A)•sin(5x)+(2•A+5•B)•cos(5x))) + 4(e2x(Acos(5x) + Bsin(5x))) = e2•x•sin(5•x)
или -25•A•e2x•cos(5x)-25•B•e2x•sin(5x) = e2•x•sin(5•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 0;B = -1/25;
Частное решение имеет вид: y* = e2x(0cos(5x) -1/25sin(5x)) илиy* =-1/25 e2x sin(5x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Используем начальные условия
Тогда окончательно,
Характеристическое уравнение исходного дифференциального уравнения 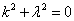
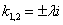
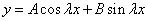
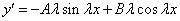
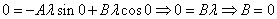
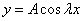
Подставляем во второе граничное условие
При А=0 и В=0 – тривиальное решение у=0
Поэтому 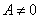
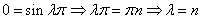
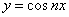
Метод исключения неизвестных.
Продифференцируем по х первое уравнение
Исключая с помощью второго уравнения 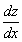
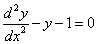
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение 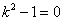
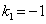
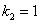
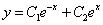
Частное решение неоднородного уравнения будем искать в виде 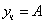
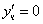
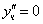
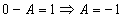
Тогда частное решение
Общее решение неоднородного примет вид:
Из первого уравнения
Ответ:
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 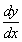
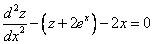
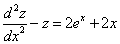
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение 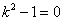
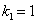
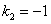
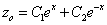
Частное решение неоднородного уравнения будем искать в виде 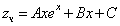
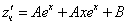
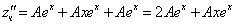
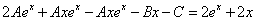
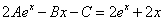
Тогда частное решение
Общее решение неоднородного примет вид:
Из второго уравнения
Ответ:
Вариант 5
Данное уравнение – уравнение с разделяющимися переменными. Разделим переменные: 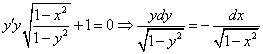
Посчитаем интегралы отдельно:
Тогда: 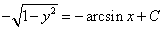
Ответ:
Это уравнение вида 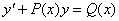


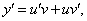
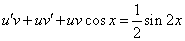
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Интегрируя, находим
Подставим найденную функцию v во второе уравнение 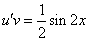
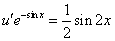
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Используем условие 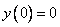
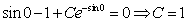
Ответ:
Данное уравнение не содержит у, следовательно понизить его порядок можно с помощью подстановки 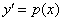
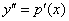
Отсюда 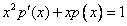
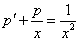
Замена 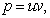
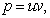
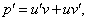
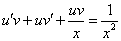
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 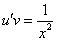
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Ответ:
Решим соответствующее однородное уравнение
Составим характеристическое уравнение 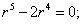
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид
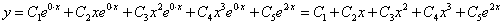
Частное решение неоднородного уравнения будем искать в виде 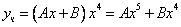
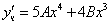
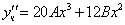
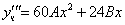
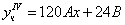
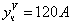
Подставим в исходное 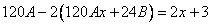
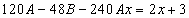
Тогда частное решение
Общее решение неоднородного примет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 — r= 0
Вынесем r за скобку. Получим: r(r-1) = 0
Корни характеристического уравнения:r1 = 0, r2 = 1
Следовательно, фундаментальную систему решений составляют функции: y1 = e0x, y2 = ex.
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) =
Уравнение имеет частное решение вида:
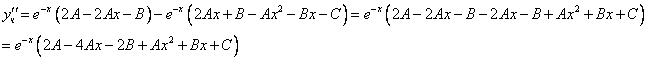
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Частное решение имеет вид:
Таким образом, общее решение дифференциального уравнения имеет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
Корни характеристического уравнения:(комплексные корни): r1 = 4i, 
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = 16•cos(4•x)-16•e4x, будем искать отдельно частные решения для f1(x)= 16•cos(4•x) и для f2(x)= 16•e4x
Для f1(x) = 16•cos(4•x) имеем
Уравнение имеет частное решение вида: y ч1* = x (Acos(4x) + Bsin(4x))
Которые подставляем в исходное дифференциальное уравнение:
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 0;B = 2;
Частное решение имеет вид: yч1* = x (0cos(4x) + 2sin(4x)) или y ч1* = 2xsin(4x)
Частное решение ищем в виде y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 16, Q(x) = 0, α = 4, β = 0.
Следовательно, число α + βi = 4 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
Которые подставляем в исходное дифференциальное уравнение:
Y» + 16y = (16•A•e4x) + 16(Ae4x) = 16•e4•x или 32•A•e4x = 16•e4•x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 1/2;
Частное решение имеет вид: y*ч2 = 1/2e4x
Таким образом, общее решение дифференциального уравнения имеет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 9 = 0
Корни характеристического уравнения: r1 = -3i, r2 = 3i
Общее решение однородного уравнения имеет вид:
Для поиска частного решения воспользуемся методом вариации произвольных постоянных. Для этого решим систему:
Тогда окончательно
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 1 = 0
Корни характеристического уравнения:(комплексные корни): r1 = i,
Следовательно, фундаментальную систему решений составляют функции:
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = 2•cos(3•x)-3•sin(3•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 2, Q(x) = -3, α = 0, β = 3.
Следовательно, число α + βi = 0 + 3i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y* = Acos(3x) + Bsin(3x)
Которые подставляем в исходное дифференциальное уравнение:
Y» + y = (-9(A•cos(3x)+B•sin(3x))) + (Acos(3x) + Bsin(3x)) = 2•cos(3•x)-3•sin(3•x)
или -8•A•cos(3x)-8•B•sin(3x) = 2•cos(3•x)-3•sin(3•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = -1/4;B = 3/8;
Частное решение имеет вид: y* = -1/4cos(3x) + 3/8sin(3x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Используем начальные условия
Тогда окончательно,
Характеристическое уравнение исходного дифференциального уравнения 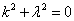
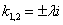
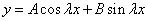
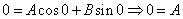
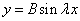
Подставляем во второе граничное условие
При А=0 и В=0 – тривиальное решение у=0
Поэтому 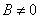
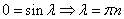
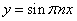
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 
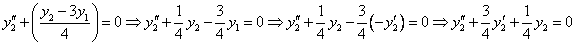
Таким образом, задача свелась к линейному однородному уравнению с постоянными коэффициентами второго порядка. Характеристическое уравнение 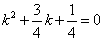
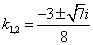
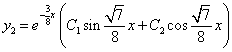
Из второго уравнения
Ответ:
Найдём сначала общее решение соответствующей однородной системы
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 
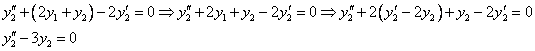
Таким образом, задача свелась к линейному однородному уравнению с постоянными коэффициентами второго порядка. Характеристическое уравнение 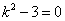
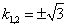
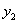
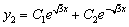
Из второго уравнения 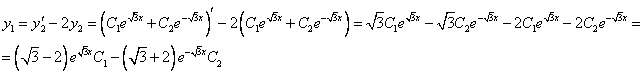
Принимаем частное решение первоначальной системы в виде:
Решаем данную систему по формулам Крамера, получим два дифференциальных уравнения первого порядка:
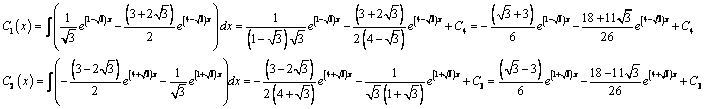
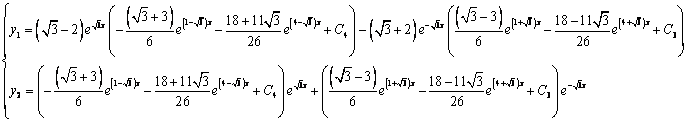
Ответ:
Контрольная работа на тему: решение однородных дифференциальных уравнений
Задание: Решение однородных дифференциальных уравнений.
Цель: формирование умений решать однородные дифференциальные уравнения первого порядка.
Задание для самостоятельной внеаудиторной работы:
46.1. Какие дифференциальные уравнения первого порядка называют однородными? Какова техника их решения?
46.2. Решите однородное дифференциальное уравнение:
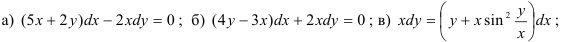
46.3. Решите однородное дифференциальное уравнение:
Методические указания по выполнению работы:
Однородные дифференциальные уравнения — уравнения вида 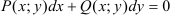
Функция 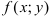
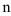
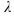
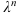
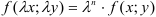
Для решения однородных дифференциальных уравнений удобно использовать следующий алгоритм:
- Выполните подстановки:
и
. В получившемся дифференциальном уравнении раскройте скобки и приведите подобные слагаемые. Должно получиться уравнение с разделяющимися переменными.
- Проинтегрируйте обе части уравнения с разделяющимися переменными относительно переменных
и
. Найдите общее решение дифференциального уравнения.
- В общем решении вернитесь к переменным
и
, подставив вместо
выражение
.
- Выпишите в ответе получившееся общее решение дифференциального уравнения.
Пример 1.
Найдите решение дифференциального уравнения: 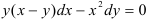
Решение:
Данное уравнение — однородное дифференциальное уравнение первого порядка.
1. Выполним подстановки: 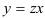
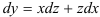
Приведем подобные слагаемые: первое и последнее взаимно уничтожаются. Получим:
Перед нами уравнение с разделяющимися переменными. Соберем в левой части выражения, содержащие 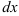
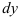
Тогда 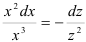
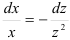
2. Интегрируя обе части, получим: 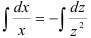
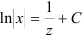
3. Подставим вместо 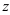
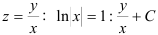
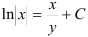
Ответ: 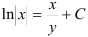
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://matica.org.ua/primery/primery/differentcialnye-uravneniia-varianty
http://lfirmal.com/kontrolnaya-rabota-na-temu-reshenie-odnorodnyih-differentsialnyih-uravnenij/













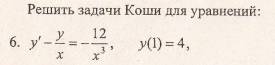
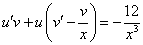
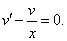
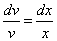
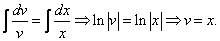
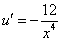
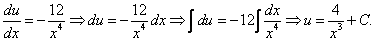
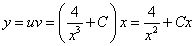
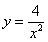
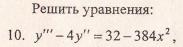
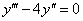
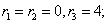
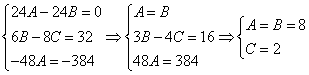
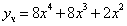
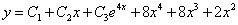

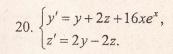
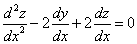
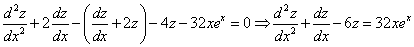
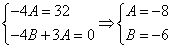
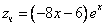
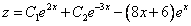

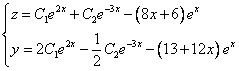
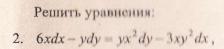
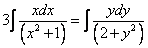

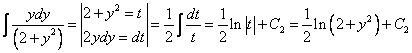
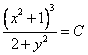
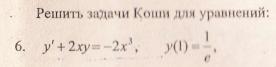
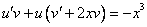
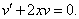
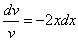
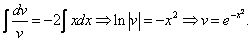
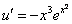
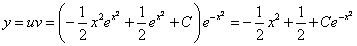
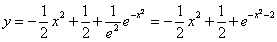
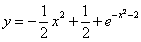
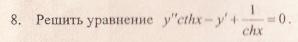
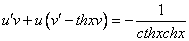
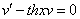
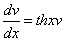
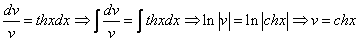
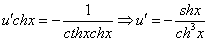

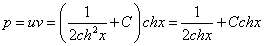
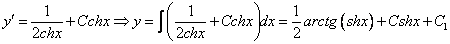
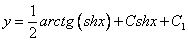
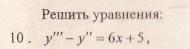
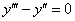
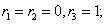
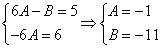
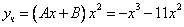
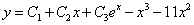
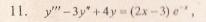
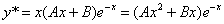
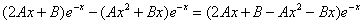
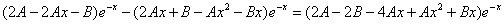
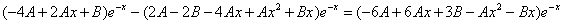
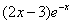
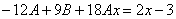
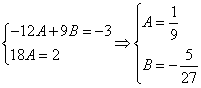
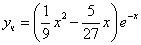
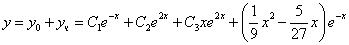
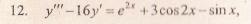
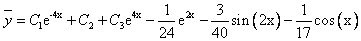

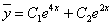
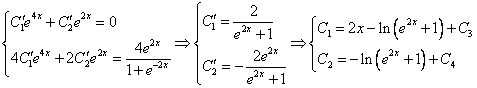
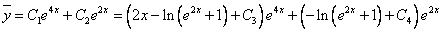
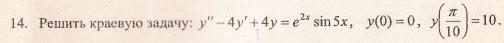
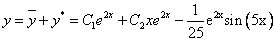
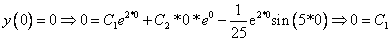
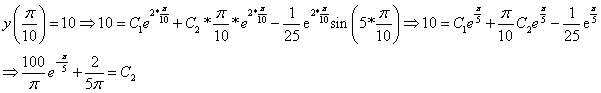

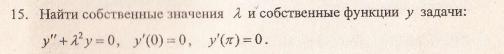
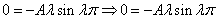
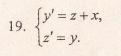
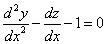
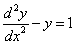
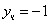
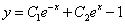
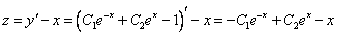
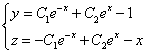
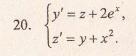
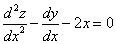
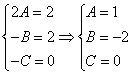
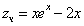
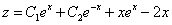
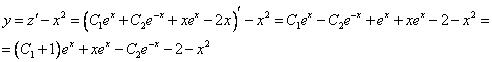
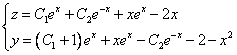
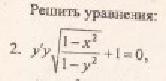
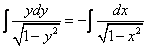
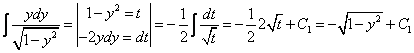
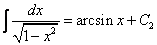
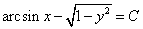
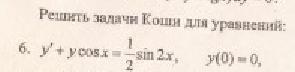
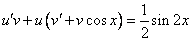
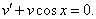
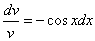
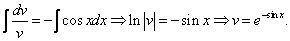
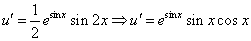

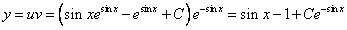
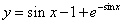

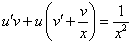
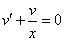
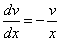
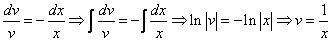
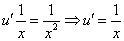
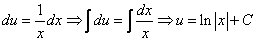
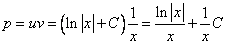
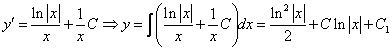
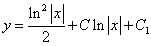
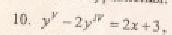
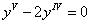
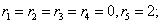
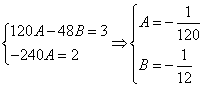
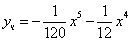
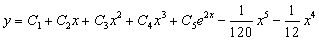

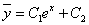
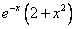
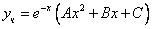
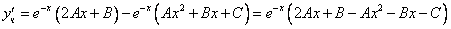
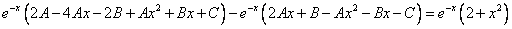
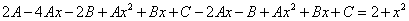
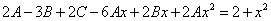
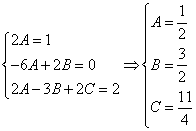
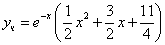
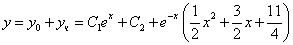
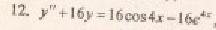
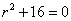
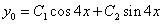
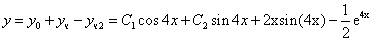
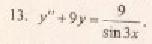
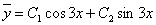
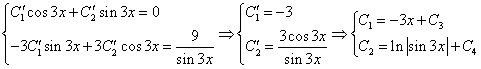
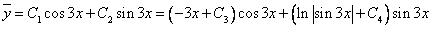

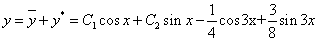
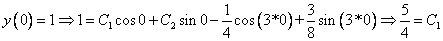
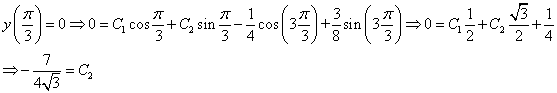
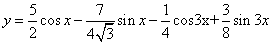
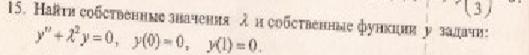
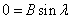
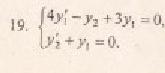
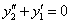


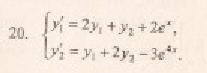
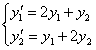
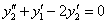
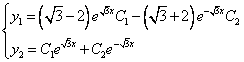
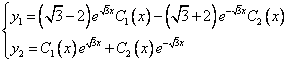
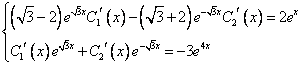

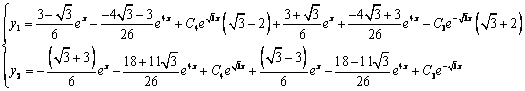
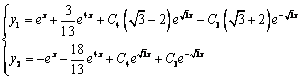
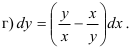
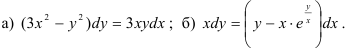
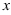 и
и 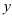 , подставив вместо
, подставив вместо 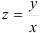 .
.