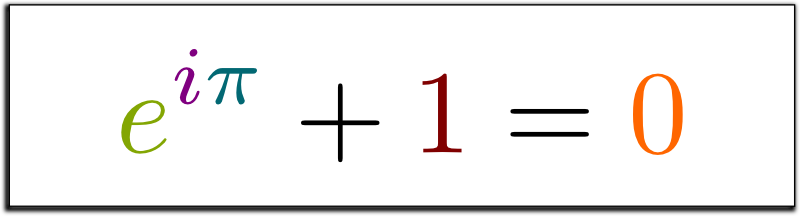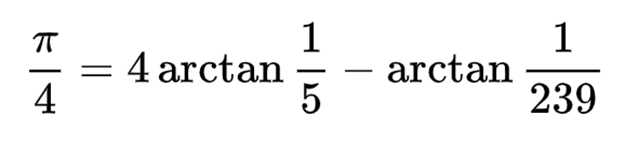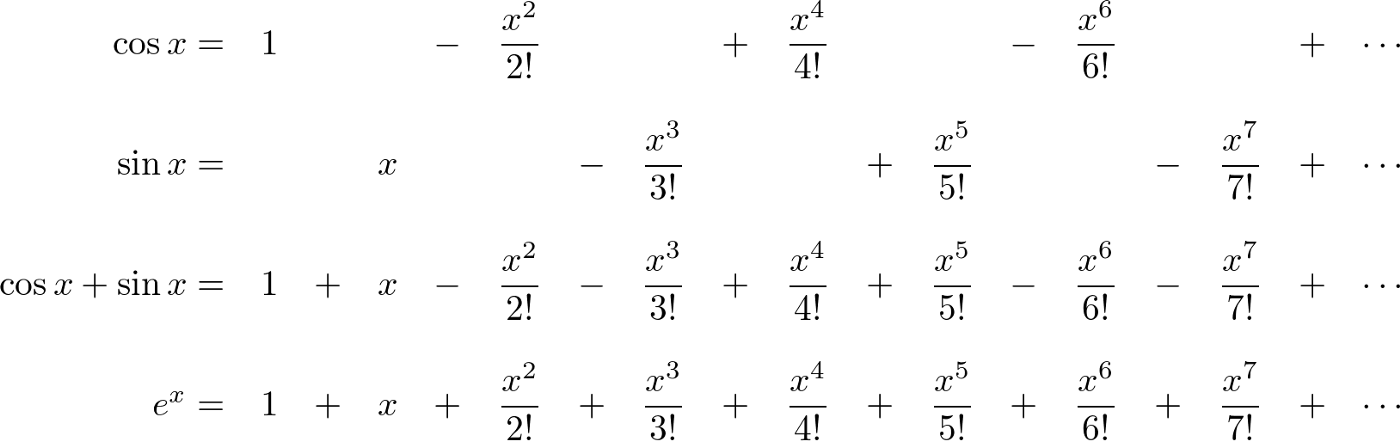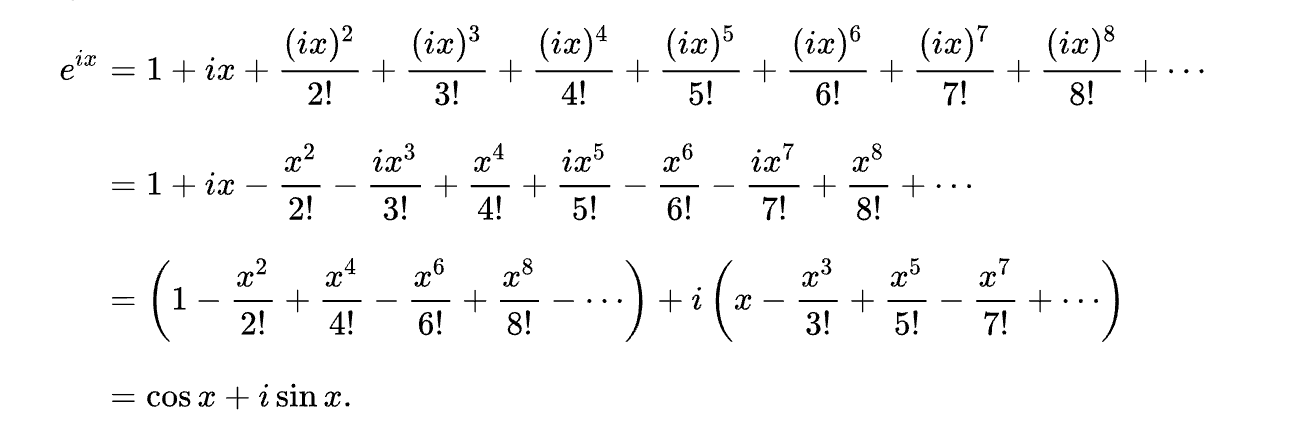Самые красивые уравнения в физике

Выводы Дирака. Уравнение Дирака. Квантовая теория поля

Данная статья посвящена работе Поля Дирака, уравнение которого значительно обогатило квантовую механику. Она описывает основные понятия, необходимые для того, чтобы разобраться в физическом смысле уравнения, а также способы его применения.

Наука и ученые

Человек, не связанный с наукой, представляет процесс добычи знаний каким-то магическим действием. А ученые, по мнению таких людей, — это чудаки, которые говорят на непонятном языке и слегка высокомерны. Знакомясь с исследователем, далекий от науки человек сразу говорит, что он в школе физику не понимал. Таким образом обыватель отгораживается от научного знания и просит более образованного собеседника говорить проще и понятнее. Наверняка Поля Дирака, уравнение которого мы рассматриваем, приветствовали так же.

Элементарные частицы

Строение вещества всегда волновало любознательные умы. В Древней Греции люди заметили, что мраморные ступени, по которым прошло множество ног, со временем меняют форму, и предположили: каждая ступня или сандалия уносила с собой крошечную частицу вещества. Эти элементы решили назвать «атомами», то есть «неделимыми». Наименование осталось, но выяснилось, что и атомы, и частицы, из которых состоят атомы, — тоже составные, сложные. Эти частицы называются элементарными. Именно им посвящена работа Дирака, уравнение которого позволило не только объяснить спин электрона, но и предположить наличие антиэлектрона.

Корпускулярно-волновой дуализм

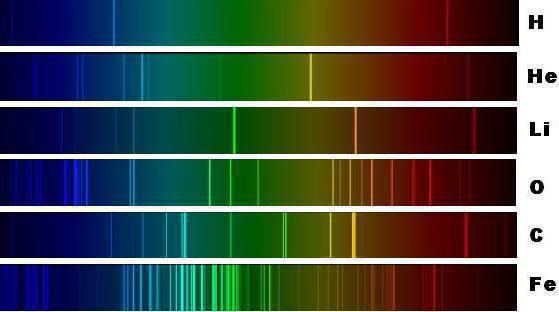
Развитие техники фотографии в конце девятнадцатого века повлекло за собой не только моду на запечатление себя, еды и кошек, но и продвинуло возможности науки. Получив такой удобный инструмент, как быстрая фотография (напомним, раньше выдержки доходили до 30-40 минут), ученые стали массово фиксировать разнообразные спектры.

Существующие на тот момент теории строения веществ не могли однозначно объяснить или предсказать спектры сложных молекул. Сначала знаменитый опыт Резерфорда доказал, что атом не такой уж неделимый: в его центре находилось тяжелое положительное ядро, вокруг которого располагались легкие отрицательные электроны. Потом открытие радиоактивности доказало, что и ядро не монолит, а состоит из протонов и нейтронов. А дальше почти одновременное открытие кванта энергии, принципа неопределенности Гейзенберга и вероятностной природы местоположения элементарных частиц дали толчок к развитию принципиально иного научного подхода к изучению окружающего мира. Появился новый раздел – физика элементарных частиц.

Основным вопросом на заре этого века великих открытий в сверхмалых масштабах стало объяснение наличия у элементарных частиц и массы, и свойств волны.

Эйнштейн доказал, что даже неуловимый фотон обладает массой, так как передает импульс твердому телу, на который падает (явление давления света). При этом многочисленные опыты по рассеянию электронов на щелях говорили как минимум о наличии у них дифракции и интерференции, это свойственно только волне. В итоге пришлось признать: элементарные частицы одновременно и объект с массой, и волна. То есть масса, скажем, электрона как бы «размазана» в пакет энергии с волновыми свойствами. Этот принцип корпускулярно-волнового дуализма позволил объяснить прежде всего, почему электрон не падает на ядро, а также по каким причинам в атоме существуют орбиты, а переходы между ними скачкообразные. Эти переходы и порождают спектр, уникальный для любого вещества. Далее физика элементарных частиц должна была объяснить свойства самих частиц, а также их взаимодействие.

Волновая функция и квантовые числа

Эрвин Шредингер совершил удивительное и до сих пор малопонятное открытие (на его основании чуть позже Поль Дирак построил свою теорию). Он доказал, что состояние любой элементарной частицы, например, электрона описывает волновая функция ψ. Сама по себе она ничего не значит, а вот ее квадрат покажет вероятность найти электрон в данном месте пространства. При этом состояние элементарной частицы в атоме (или другой системе) описывается четырьмя квантовыми числами. Это главное (n), орбитальное (l), магнитное (m) и спиновое (m_s) числа. Они показывают свойства элементарной частицы. Как аналогию можно привести брусок масла. Его характеристики – масса, размер, цвет и жирность. Однако свойства, описывающие элементарные частицы, нельзя понять интуитивно, их надо осознавать через математическое описание. Работа Дирака, уравнение которого — в центре внимания этой статьи, посвящена последнему, спиновому числу.

Прежде чем перейти непосредственно к уравнению, необходимо объяснить, что же обозначает спиновое число m_s. Оно показывает собственный момент импульса электрона и других элементарных частиц. Это число всегда положительно и может принимать целое значение, ноль или полуцелое значение (для электрона m_s = 1/2). Спин – величина векторная и единственная, которая описывает ориентацию электрона. Квантовая теория поля кладет спин в основу обменного взаимодействия, которому нет никакого аналога в обычно интуитивно понятной механике. Спиновое число показывает, каким образом должен повернуться вектор, чтобы прийти в изначальное состояние. Примером может служить обычная шариковая ручка (пишущая часть пусть будет положительным направлением вектора). Чтобы она пришла в изначальное состояние, ее надо повернуть на 360 градусов. Такая ситуация соответствует спину, равному 1. При спине 1/2, как у электрона, поворот должен быть 720 градусов. Так что, помимо математического чутья, надо иметь развитое пространственное мышление, чтобы понять это свойство. Чуть выше шла речь о волновой функции. Она является основным «действующим лицом» уравнения Шредингера, с помощью которого описывается состояние и положение элементарной частицы. Но это соотношение в своем изначальном виде предназначено для частиц без спина. Описать состояние электрона можно, только если провести обобщение уравнения Шредингера, что и было проделано в работе Дирака.

Бозоны и фермионы

Фермион – частица с полуцелым значением спина. Фермионы располагаются в системах (например атомах) согласно принципу Паули: в каждом состоянии должно быть не более одной частицы. Таким образом, в атоме каждый электрон чем-то отличается от всех остальных (какое-то квантовое число имеет другое значение). Квантовая теория поля описывает и другой случай – бозоны. Они имеют целый спин и могут все одновременно быть в одном состоянии. Реализация этого случая называет Бозе-конденсацией. Несмотря на достаточно хорошо подтвержденную теоретическую возможность его получить, практически это осуществили только в 1995 году.

Уравнение Дирака

Как мы уже говорили выше, Поль Дирак вывел уравнение классического поля электрона. Оно также описывает состояния других фермионов. Физический смысл соотношения сложен и многогранен, и из его формы следует много фундаментальных выводов. Вид уравнения следующий:

где m — масса фермиона (в частности электрона), с — скорость света, p_k— три оператора компонент импульса (по осям x, y, z), ħ — урезанная постоянная Планка, x и t – три пространственные координаты (соответствуют осям X, Y, Z) и время, соответственно, и ψ(x, t) — четырёхкомпонентная комплексная волновая функция, α_k (k=0, 1, 2, 3) — матрицы Паули. Последние представляют собой линейные операторы, которые действуют на волновую функцию и ее пространство. Формула эта довольно сложная. Чтобы понять хотя бы ее компоненты, надо разбираться в основных определениях квантовой механики. Также следует обладать недюжинными математическими познаниями, чтобы как минимум знать, что такое вектор, матрица и оператор. Специалисту вид уравнения скажет еще больше, чем его компоненты. Человек, сведущий в ядерной физике и знакомый с квантовой механикой, поймет важность этого соотношения. Однако надо признаться, что уравнения Дирака и Шредингера — всего лишь элементарные основы математического описания процессов, которые происходят в мире квантовых величин. Физики-теоретики, которые решили посвятить себя элементарным частицам и их взаимодействию, должны понимать суть этих соотношений на первом-втором курсах института. Но наука эта увлекательная, и именно в этой области можно совершить прорыв или увековечить свое имя, присвоив его уравнению, преобразованию или свойству.

Физический смысл уравнения

Как мы и обещали, рассказываем, какие выводы таит уравнение Дирака для электрона. Во-первых, из этого соотношения становится ясно, что спин электрона равен ½. Во-вторых, согласно уравнению, у электрона есть собственный магнитный момент. Он равен магнетону Бора (единица элементарного магнитного момента). Но самый главный результат получения этого соотношения кроется в незаметном операторе α_k. Вывод уравнения Дирака из уравнения Шредингера занял много времени. Вначале Дирак думал, что эти операторы мешают соотношению. С помощью разных математических ухищрений он пытался исключить их из уравнения, но ему это не удалось. В итоге уравнение Дирака для свободной частицы содержит четыре оператора α. Каждый из них представляет собой матрицу [4×4]. Два соответствуют положительной массе электрона, что доказывает наличие двух положений его спина. Другие же два дают решение для отрицательной массы частицы. Самые простые познания в физике предоставляют человеку возможность заключить, что это невозможно в реальности. Но в результате эксперимента выяснилось, что последние две матрицы являются решениями для существующей частицы, противоположной электрону – антиэлектрону. Как и электрон, позитрон (так назвали эту частицу) обладает массой, но его заряд положителен.

Позитрон

Как часто бывало в эру квантовых открытий, Дирак сначала не поверил собственному выводу. Он не решился открыто опубликовать предсказание новой частицы. Правда, во множестве статей и на различных симпозиумах ученый подчеркивал возможность ее существования, хотя и не постулировал это. Но вскоре после вывода этого знаменитого соотношения позитрон был найден в составе космического излучения. Таким образом, его существование было подтверждено эмпирически. Позитрон – первый найденный людьми элемент антиматерии. Позитрон рождается как один из близнецов пары (другой близнец – это электрон) при взаимодействии фотонов очень высокой энергии с ядрами материи в сильном электрическом поле. Приводить цифры мы не будем (заинтересованный читатель и сам найдет всю нужную информацию). Однако стоит подчеркнуть, что речь идет о космических масштабах. Произвести фотоны нужной энергии способны лишь взрывы сверхновых и столкновения галактик. Также они в некотором количестве содержатся в ядрах горячих звезд, в том числе Солнца. Но человек всегда стремится к своей выгоде. Аннигиляция материи с антиматерией дает много энергии. Чтобы обуздать этот процесс и пустить его на благо человечества (например, эффективными были бы двигатели межзвездных лайнеров на аннигиляции), люди научились изготавливать протоны в лабораторных условиях.

В частности, большие ускорители (типа адронного коллайдера) могут создавать пары электрон-позитрон. Раньше также высказывались предположения, что существуют не только элементарные античастицы (помимо электрона их еще несколько), но и целая антиматерия. Даже совсем небольшой кусочек любого кристалла из антивещества обеспечил бы энергией всю планету (может быть, криптонит супермена был антиматерией?).

Но увы, создание антиматерии тяжелее ядер водорода в обозримой вселенной задокументировано не было. Однако если читатель думает, что взаимодействие вещества (подчеркнем, именно вещества, а не отдельно взятого электрона) с позитроном сразу заканчивается аннигиляцией, то он ошибается. При торможении позитрона с высокой скоростью в некоторых жидкостях с ненулевой вероятностью возникает связанная пара электрон-позитрон, которая называется позитроний. Это образование имеет некоторые свойства атома и даже способно вступать в химические реакции. Но существует этот хрупкий тандем недолго и потом все равно аннигилирует с испусканием двух, а в некоторых случаях и трех гамма-квантов.

Недостатки уравнения

Несмотря на то что благодаря этому соотношению был обнаружен антиэлектрон и антиматерия, оно имеет существенный недостаток. Запись уравнения и модель, построенная на его основе, не способны предсказать, как рождаются и уничтожаются частицы. Это своеобразная ирония квантового мира: теория, предсказавшая рождение пар материя-антиматерия, не способна адекватно описать этот процесс. Данный недостаток был устранен в квантовой теории поля. Путем введения квантованности полей эта модель описывает их взаимодействие, в том числе рождение и уничтожение элементарных частиц. Под «квантовой теорией поля» в данном случае подразумевается совершенно конкретный термин. Это область физики, которая изучает поведение квантовых полей.

Уравнение Дирака в цилиндрических координатах

Для начала сообщим, что такое цилиндрическая система координат. Вместо привычных трех взаимно перпендикулярных осей для определения точного местоположения точки в пространстве используются угол, радиус и высота. Это то же самое, что полярная система координат на плоскости, только добавляется третье измерение – высота. Эта система удобна, если требуется описать или исследовать некоторую поверхность, симметричную относительно одной из осей. Для квантовой механики это весьма полезный и удобный инструмент, который позволяет значительно сократить размер формул и количество вычислений. Это следствие осесимметричности электронного облака в атоме. Уравнение Дирака в цилиндрических координатах решается несколько иначе, чем в привычной системе, и дает иногда неожиданные результаты. Например, некоторые прикладные задачи по определению поведения элементарных частиц (чаще всего электронов) в квантованном поле решались преобразованием вида уравнения к цилиндрическим координатам.

Использование уравнения для определения строения частиц

Это равенство описывает простые частицы: такие, которые не состоят из еще более мелких элементов. Современная наука способна измерять магнитные моменты с достаточно высокой точностью. Таким образом, несоответствие посчитанного с помощью уравнения Дирака значения измеренному экспериментально магнитному моменту будет косвенно свидетельствовать о сложном строении частицы. Напомним, это равенство применимо к фермионам, их спин полуцелый. С помощью этого уравнения была подтверждена сложная структура протонов и нейтронов. Каждый из них состоит из еще более мелких элементов, которые называются кварками. Глюонное поле держит кварки вместе, не давая им рассыпаться. Существует теория, что и кварки — это не самые элементарные частицы нашего мира. Но пока у людей не хватает технической мощи, чтобы это проверить.

Самая красивая теорема математики: тождество Эйлера

Посмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением. Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу.

Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».

Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.

Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».

Рисунок 2.0: обложка журнала The Mathematical Intelligencer

Рисунок 3.0: опрос Дэвида Уэллса из журнала

Леонарда Эйлера называют самым продуктивным математиком за всю историю. Других выдающихся математиков вдохновляли его работы. Один из лучших физиков в мире, Ричард Фейнман, в своих знаменитых лекциях по физике назвал уравнение Эйлера «самой примечательной формулой в математике». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу «…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой».

Существует множество интересных фактов об уравнении Эйлера. Например, оно встречалось в некоторых эпизодах «Симпсонов».

Рисунок 4.0: в этой сцене уравнение Эйлера можно заметить на второй книге в самой правой стопке.

Рисунок 5.0: в этой сцене уравнение Эйлера написано на футболке второстепенного персонажа.

Также уравнение Эйлера стало ключевым пунктом в уголовном деле. В 2003 году аспирант Калифорнийского технологического института Билли Коттрелл писал краской на чужих спортивных автомобилях уравнение Эйлера. На суде он сказал: «Я знал теорему Эйлера с пяти лет, и её обязаны знать все«.

Рисунок 6.0: марка, выпущенная в 1983 году в Германии в память о двухсотлетии со смерти Эйлера.

Рисунок 7.0: марка, выпущенная Швейцарией в 1957 году в честь 250-й годовщины Эйлера.

Почему уравнение Эйлера так важно?

Вы имеете полное право задаться вопросом: почему Билли Коттрелл считал, что об уравнении Эйлера обязаны знать все? И был настолько в этом уверен, что начал писать его на чужих машинах? Ответ прост: Эйлер воспользовался тремя фундаментальными константами математики и применил математические операции умножения и возведения в степень, чтобы записать красивую формулу, дающую в результате ноль или минус один.

• Константа e связана со степенными функциями.
• Константа i является не вещественным, а мнимым числом, равным квадратному корню из минус единицы.
• Знаменитая константа π (пи) связана с окружностями.

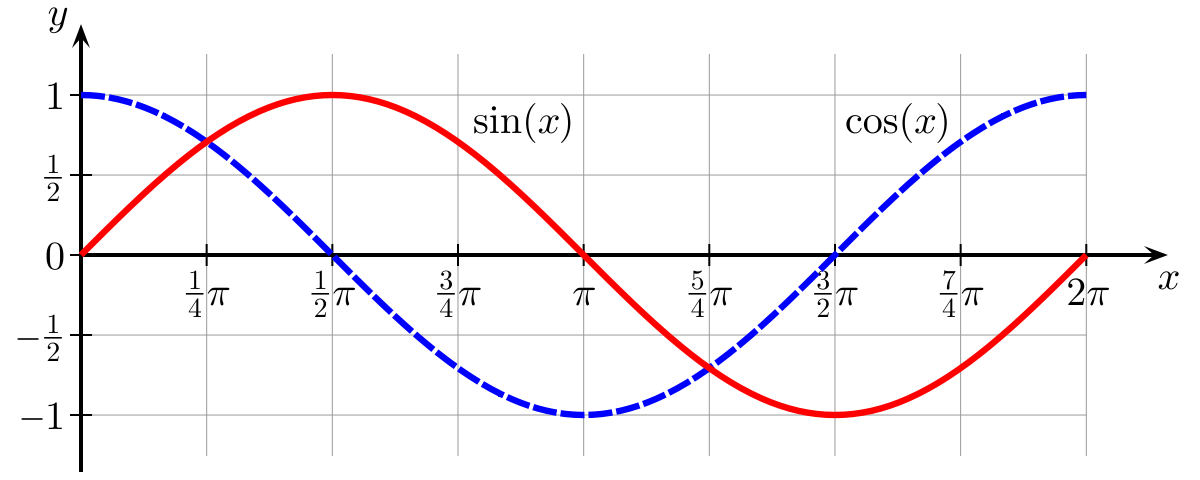
Впервые тождество Эйлера появилось в 1748 году в его книге Introductio in analysin infinitorum. Позже другие люди увидели, что эта формула связана с тригонометрическими функциями синуса и косинуса, и эта связь удивительна, ведь степенная функция стремится к бесконечности, а тригонометрические функции колеблются в интервале от — 1 до -1.

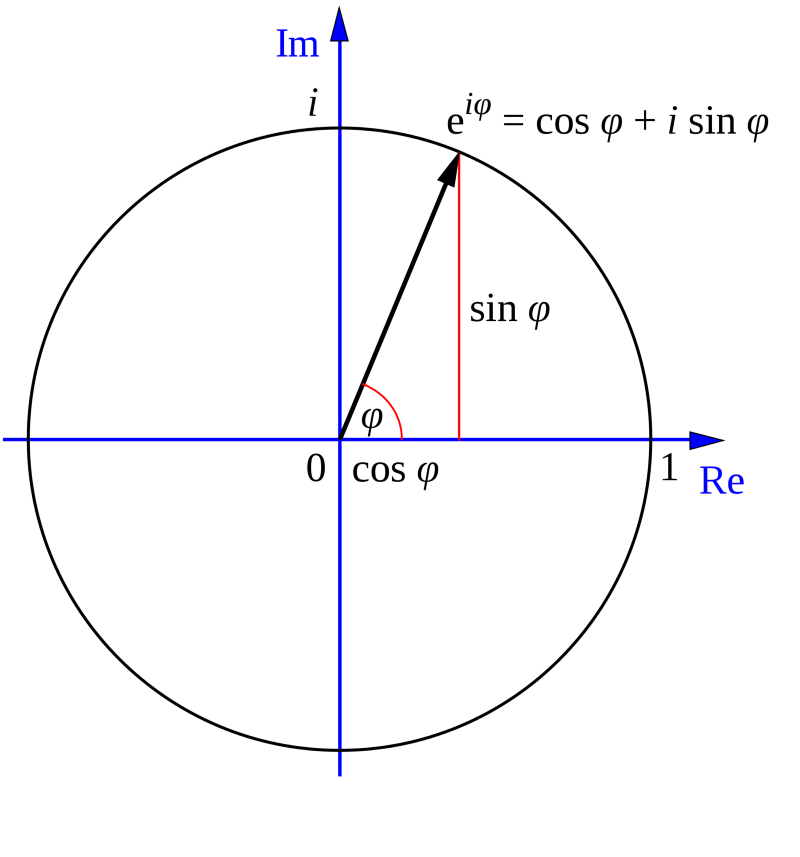
e в степени i, умноженного на ϕ (фи) = cos ϕ + i * sin ϕ

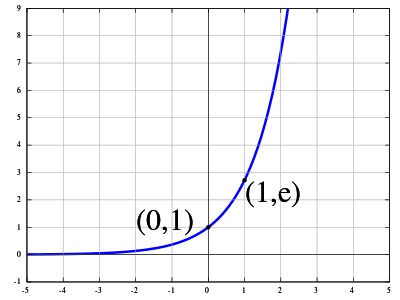
Рисунок 8.0: экспоненциальная функция y=e x .

Рисунок 8.1: график тождества Эйлера.

Рисунок 8.2: частоты, испускаемые LC-цепью.

Показанные выше уравнения и графы могут показаться абстрактными, но они важны для квантовой физики и вычислений обработки изображений, и при этом зависят от тождества Эйлера.

1: число для счёта

Число 1 (единица) является основой нашей системы исчисления. С неё мы начинаем счёт. Но как мы считаем? Чтобы считать, мы используем цифры 0–9 и систему разрядов, определяющую значение цифры.

Например, число 323 означает 3 сотни, 2 десятка и 3 единицы. Здесь число 3 исполняет две разные роли, которые зависят от его расположения.

323 = (3*100) + (2*10) + (3*1)

Существует и другая система исчисления, называемая двоичной. В этой системе вместо 10 используется основание 2. Она широко применяется в компьютерах и программировании. Например, в двоичной системе:

1001 = (2 3 ) + (0 2 ) + (0 1 ) + (2 0 ) = [9 в системе с основанием 10]

Кто создал системы исчисления? Как первые люди считали предметы или животных?

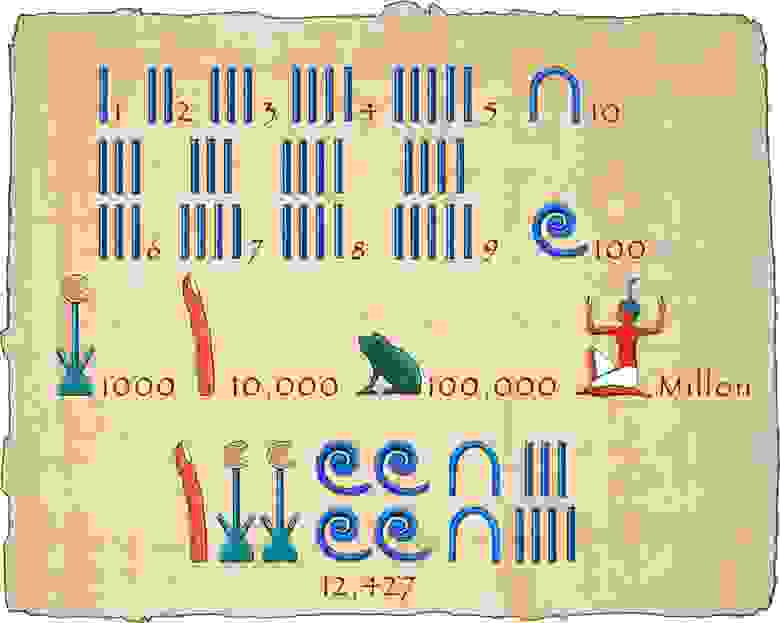
Как возникли наши системы исчисления? Как считали первые цивилизации? Мы точно знаем, что они не пользовались нашей разрядной системой. Например 4000 лет назад древние египтяне использовали систему исчисления с разными символами. Однако они комбинировали символы, создавая новый символ, обозначающий числа.

Рисунок 11: показанные здесь иероглифы образуют число 4622; это одно из чисел, вырезанных на стене в храме в Карнаке (Египет).

Рисунок 12: иероглифы — это изображения, обозначающие слова, а в данном случае — числа.

В то же время, но в другом месте ещё один социум обнаружил способ подсчёта, но в нём тоже использовались символы. Кроме того, основанием их системы исчисления было 60, а не 10. Мы используем их метод счёта для определения времени; поэтому в минуте 60 секунд, а в часе 60 минут.

Рисунок 13: вавилонские числа из шестидесятиричной системы счисления (с основанием 60).

Тысячу лет спустя древние римляне изобрели римские числа. Для обозначения чисел они использовали буквы. Римская нотация не считается разрядной системой, потому что для многих значений нашей системы счисления в ней использовались разные буквы. Именно по этой причине для счёта они использовали абакус.

Рисунок 14: романский абакус в шестнадцатеричной (с основанием 16) системе счисления

Рисунок 15: таблица преобразования из арабских в римские числа

Древние греки тоже не использовали разрядную систему счисления. Греческие математики обозначали числа буквами. У них были специальные буквы для чисел от 100 до 900. Многие люди в то время считали греческие числа запутанными.

Рисунок 15: таблица букв древних греков.

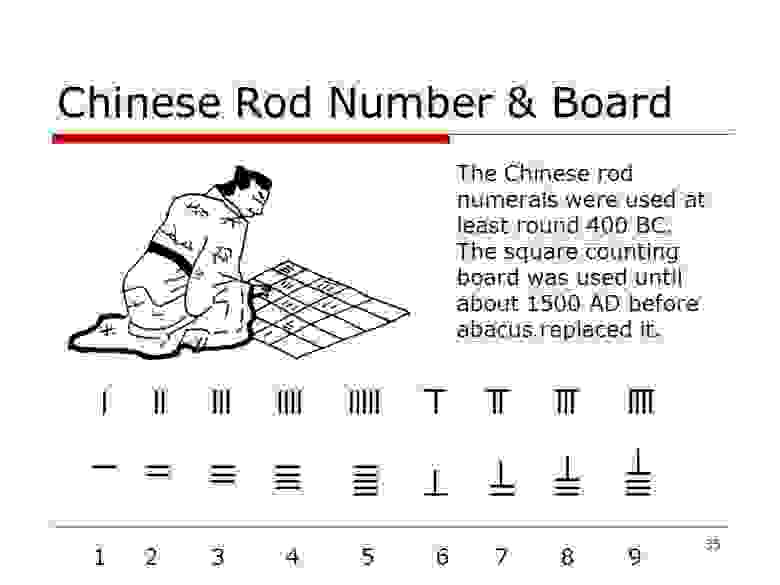
В то же самое время китайские математики начали использовать для расчётов небольшие бамбуковые палочки. Этот китайский способ счёта называют первой десятичной разрядной системой.

Рисунок 16: китайский способ счёта с числами-палочками. Использовался как минимум с 400 года до нашей эры. Квадратная счётная доска использовалась примерно до 1500 года, когда её заменил абакус.

Однако самая уникальная система счёта использовалась индейцами майя. Их система счисления имела основание 20. Для обозначения чисел от 1 до 19 они использовали точки и линии. Чем же отличалась их система счисления? Для каждого числа они использовали изображения голов и отдельный символ нуля 0.

Рисунок 17: Система счисления майя с основанием 20, в которой числа обозначались головами

Рисунок 18: ещё один способ записи чисел майя.

0: число для обозначения ничего

Некоторые цивилизации использовали пробелы, чтобы, например, отличать число 101 от 11. Спустя какое-то время начало появляться особое число — ноль. К примеру, в пещере в индийском городе Гвалиор археологи обнаружили на стене число 270, в котором был ноль. Самое первое зафиксированное использование нуля можно увидеть в Бодлианской библиотеке.

Рисунок 19: вырезанный на стене храма в Гвалиоре круг обозначает ноль. Ему примерно 1500 лет.

Рисунок 20: чёрные точки в манускрипте Бакхшали обозначают нули; это самый старый письменный пример использования числа, ему примерно 1800 лет.

Примерно 1400 лет назад были записаны правила вычислений с нулём. Например, при сложении отрицательного числа и нуля получается то же отрицательное число. Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.

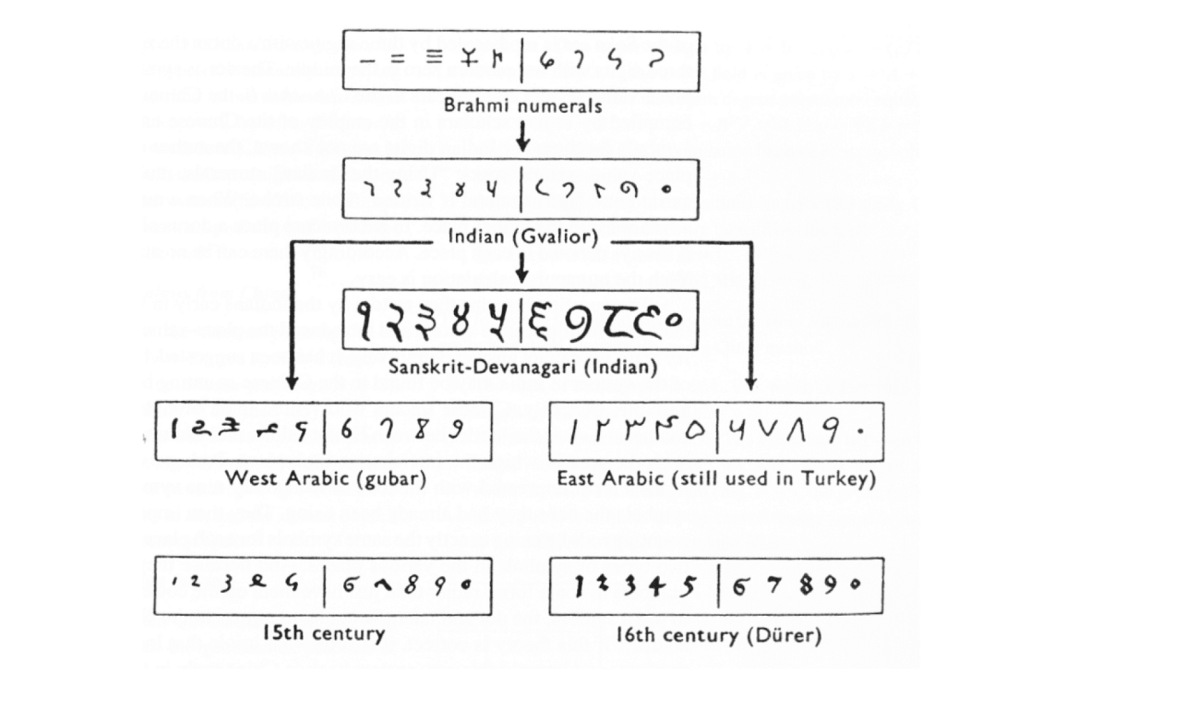
Вскоре после этого многими людьми были опубликованы книги по арифметике, распространяющие использование индо-арабской записи чисел. Ниже показана эволюция индо-арабских чисел. В большинстве стран используется индо-арабская система чисел, но арабские страны до сих пор пользуются арабскими числами.

Рисунок 21: на этой схеме показана эволюция чисел, происходящих от чисел брахми и заканчивающаяся числами, которыми мы используем и сегодня.

Рисунок 22: классическая гравюра «Арифметика» из Margarita Philosophica Грегора Рейша, на которой изображено соревнование между Боэцием, улыбающимся после открытия индо-арабских чисел и письменных вычислений, и нахмуренным Пифагором, до сих пор пытающимся пользоваться счётной доской.

Пи (π): самое известное иррациональное число

Пи — самое популярное из известных нам иррациональных чисел. Пи можно найти двумя способами: вычислив соотношение длины окружности к её диаметру, или соотношение площади круга к квадрату его радиуса. Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д.

π = окружность / диаметр ИЛИ π = площадь круга / радиус²

Рисунок 22: анимированная связь между окружностью и диаметром в отношении пи.

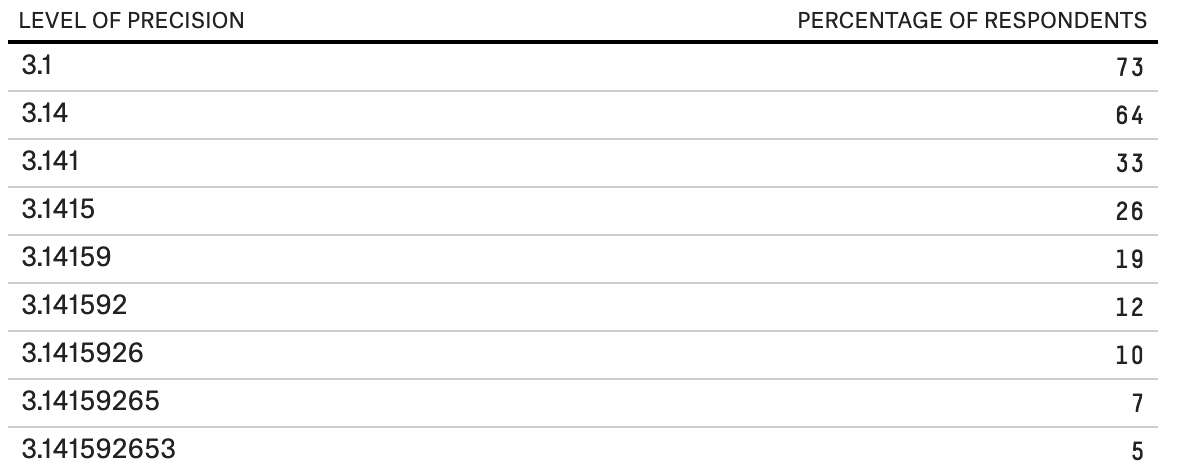
Так как иррациональные числа наподобие пи бесконечны и не имеют повторений, мы никогда не закончим записывать пи. Оно продолжается вечно. Есть люди, запомнившие множество десятичных разрядов пи (нынешний рекорд — 70 000 цифр! Источник: «Книга рекордов Гиннесса» ).

Рисунок 23: данные опроса 941 респондентов для определения процента людей, способных запомнить знаки пи после запятой.

Рисунок 24: На стене станции метро Karlsplatz в Вене записаны сотни разрядов пи.

На данный момент компьютеры смогли вычислить всего 2,7 триллиона разрядов пи. Может казаться, что это много, но на самом деле этот путь бесконечен.

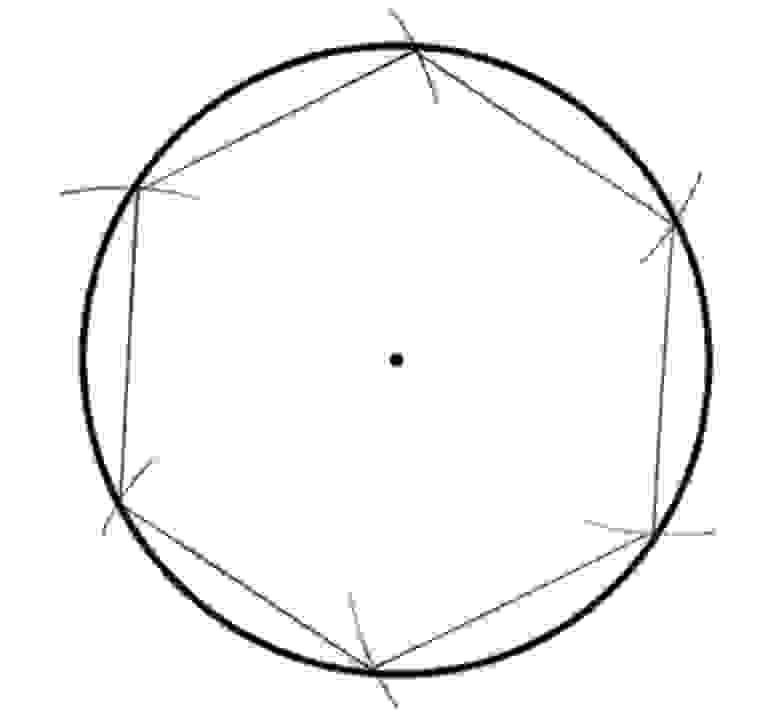
Как я сказал выше, число пи нашёл Евклид. Но как поступали люди до Евклида, когда им нужно было найти площадь круга? Историки обнаружили вавилонскую глиняную табличку, в которой было записано отношение периметра шестиугольника к диаметру описанной вокруг него окружности. После вычислений полученное число оказалось равным 3.125. Это очень близко к пи.

Рисунок 24: вавилонская глиняная табличка с отношением периметра шестиугольника к длине описанной окружности.

Древние египтяне тоже близко подобрались к значению пи. Историки обнаружили документ, показывающий, как древние египтяне нашли число пи. Когда историки перевели документ, то нашли такую задачу:

Например, чтобы найти площадь поля диаметром 9 хета (1 хет = 52,35 метра), нужно выполнить следующее вычисление:

Вычесть 1/9 диаметра, а именно 1. Остаток равен 8. Умножить его на 8, что даёт нам 64. Следовательно, площадь будет равна 64 setjat (единица измерения площади).

Другими словами, диаметр равен 2r, а 1/9 радиуса равно (1/9 • 2r). Тогда если мы вычтем это из исходного диаметра, то получим 2r — (1/9 • 2r) = 8/9(2r). Тогда площадь круга равна 256/81 r². То есть пи равно почти 3,16. Они обнаружили это значение пи примерно 4000 лет назад.

Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.

Спустя тысячу лет немецкий математик Людольф Цейлен работал со 2 62 -сторонним многоугольником и получил 35 десятичных разрядов пи. Это число, названное Людольфовым, было высечено на его могильном камне.

В 1706 году англичанин Джон Мэчин, долгое время работавший профессором астрономии, использовал формулу сложения, чтобы доказать, что пи равно

Не беспокоясь о том, как откуда взялась эта формула, Мэчин начал постоянно ею пользоваться, а затем записал показанный ниже ряд. Это был самый большой на то время шаг в количестве разрядов пи.

Однако первое упоминание пи появилось в 1706 году. Преподаватель математики Уильям Джонс написал книгу и впервые предложил пи для измерения окружностей. Так пи впервые появилась в книгах!

В 1873 году Уильям Шэнкс воспользовался формулой Джона Мэчина и получил 707 десятичных разрядов пи. Эти цифры написаны в комнате пи парижского Дворца открытий. Однако позже математики выяснили, что верными являются только 527 разрядов.

Рисунок 31: комната пи

С другой стороны, более интересный способ нахождения пи обнаружил Буффон. Его эксперимент основывался на случайном разбрасывании иголок для оценки пи. Он нарисовал на доске несколько параллельных линий на расстоянии D и взял иголки длиной L. Затем он случайным образом начал бросать иголки на доску и записывал долю иголок, пересекавших линию.

А после этого другой математик по имени Ладзарини подбросил иголку 3408 раз и получил шесть десятичных разрядов пи с соотношением 355/113. Однако если бы одна иголка не пересекла линию, он получил бы только 2 разряда пи.

Рисунок 32.1: бросание 1000 иголок для оценки приблизительного значения пи

e: история экспоненциального роста

e — это ещё одно знаменитое иррациональное число. Дробная часть e тоже бесконечна, как и у пи. Мы используем число e для вычисления степенного (экспоненциального) роста. Другими словами, мы используем e, когда видим очень быстрый рост или уменьшение.

Один из величайших, а возможно и лучший математик Леонард Эйлер открыл число e в 1736 году и впервые упомянул это особое число в своей книге Mechanica.

Чтобы разобраться в экспоненциальном росте, мы можем использовать историю об изобретателе шахмат. Когда он придумал эту игру, то показал её властителю Севера. Царю понравилась игра и он пообещал, что отдаст автору любую награду. Тогда изобретатель попросил нечто очень простое: 2 0 зерна на первую клетку шахматной доски, 2 1 зерна на вторую клетку доски, 2 2 зерна — на третью, и так далее. Каждый раз количество зерна удваивалось. Царь Севера подумал, что просьбу будет выполнить легко, но он ошибался, потому то на последнюю клетку нужно было бы положить 2 63 зёрен, что равно 9 223 372 036 854 775 808. Это и есть экспоненциальный рост. Он начался с 1, постоянно удваивался, и через 64 шага вырос в огромное число!

Если бы изобретатель шахмат выбрал линейное уравнение, например 2n, то получил бы 2, 4, 6, 8, … 128… Следовательно, в дальней перспективе экспоненциальный рост часто намного превышает полиномиальный.

Кстати, 9 223 372 036 854 775 808–1 — это максимальное значение 64-битного целого числа со знаком.

Число e открыл Эйлер. Однако Якоб Бернулли тоже работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег. Если вложить 100 долларов под 10% дохода, то как будет расти эта сумма? Во-первых, это зависит от того, как часто банк рассчитывает проценты. Например, если он рассчитывает один раз, то мы получим в конце года 110 долларов. Если мы передумаем и будем брать проценты каждые 6 месяцев, то в этом случае мы получим больше 110 долларов. Дело в ттом, что процент, полученный за первые 6 месяцев, тоже получит свой процент. Общая сумма будет равна 110,25 долларов. Можно догадаться, что мы можем получить больше денег, если будем забирать деньги каждый квартал года. А если мы будем делать временной интервал всё короче, то окончательные суммы будут продолжать расти. Такой бесконечный сложный процент сделает нас богатыми! Однако наш общий доход стремится к ограниченному значению, связанному с e.

Бернулли не называл число 2,71828 именем e. Когда Эйлер работал с 2,71828, он возвёл экспоненциальную функцию e в степень x. Свои открытия он изложил в книге The Analysis of Infinite.

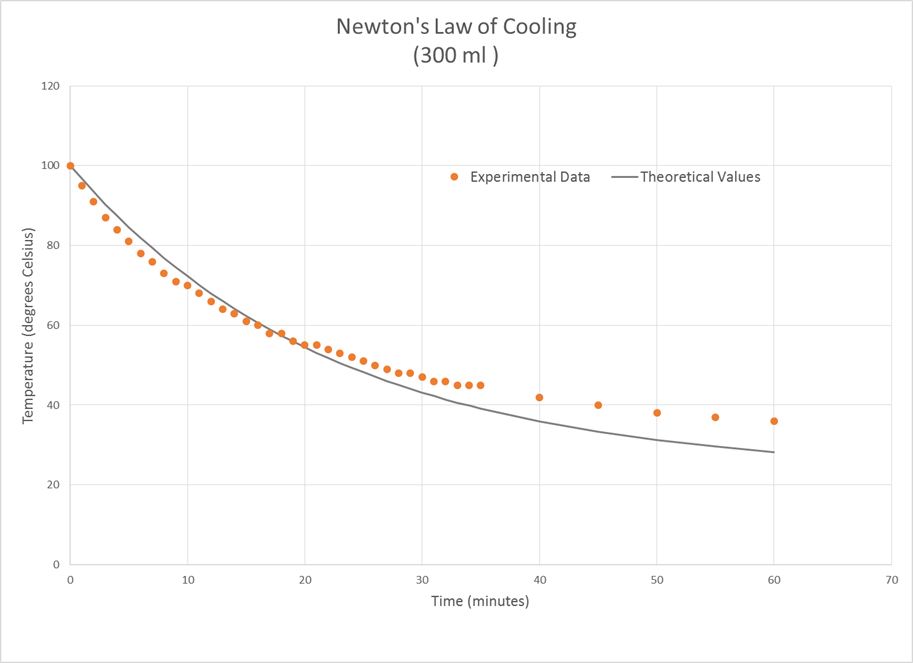
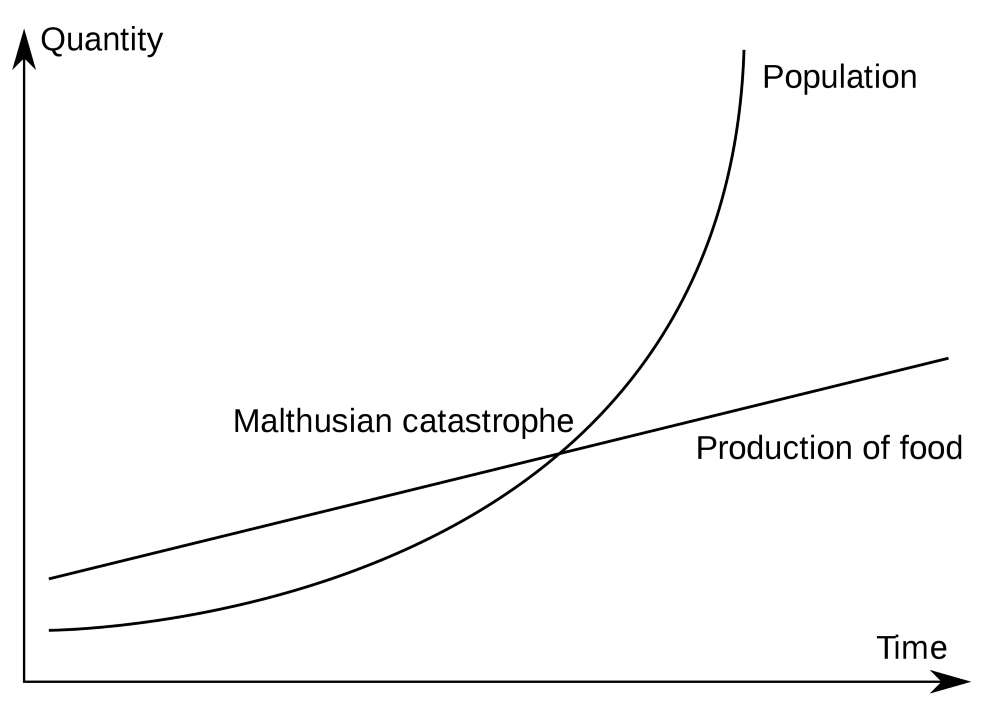
В 1798 году Томас Мальтус использовал экспоненциальную функцию в своём эссе, посвящённом пищевому дефициту будущего. Он создал линейный график, показывающий производство пищи и экспоненциальный график, показывающий население мира. Мальтус сделал вывод, что в дальней перспективе экспоненциальный рост победит, и мир ждёт серьёзный дефицит пищи. Это явление назвали «мальтузианской катастрофой». Ньютон тоже использовал эту модель, чтобы показать, как охлаждается чашка чая.

Рисунок 35: закон Ньютона-Рихмана

Рисунок 36: мальтузианская катастрофа

Мнимость числа: i, квадратный корень -1

Долгое время для решения своих задач математикам было достаточно обычных чисел. Однако в какой-то момент для дальнейшего развития им потребовалось открыть нечто новое и загадочное. Например, итальянский математик Кардано пытался разделить число 10 на 2 части, произведение которых было бы равно 40. Чтобы решить эту задачу, он записал уравнение: x (10-x) = 40. Когда он решил это квадратное уравнение, то получил два решения: 5 плюс √-15 и 5 минус √-15, что в то время не имело никакого смысла. Этот результат был бессмысленным, потому что по определению квадратного корня ему нужно было найти число, квадрат которого был бы отрицательным. Однако и положительное, и отрицательное числа в квадрате имеют положительное значение. Как бы то ни было, он нашёл своё уникальное число. Однако первым математиком, назвавшим √-1 (квадратный корень из минус единицы) мнимым числом i, был Эйлер.

Лейбниц дал такой комментарий о мнимом числе √-1:

Комплексные числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием.

Мы можем складывать, вычитать, умножать и делить мнимые числа. Сложение, вычитание и умножение просты, а деление немного сложнее. Вещественные и мнимые части складываются по отдельности. В случае умножения i 2 будет равно -1.

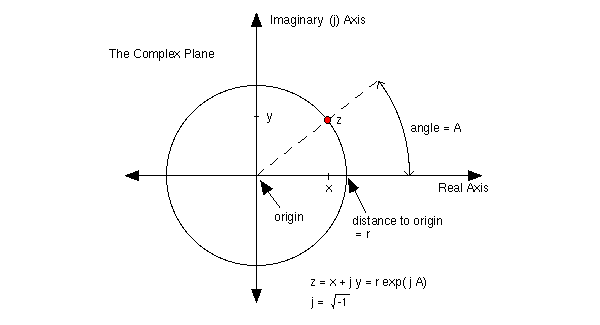
После Эйлера математик Каспар Вессель представил мнимые числа геометрически с создал комплексную плоскость. Сегодня мы представляем каждое комплексное число a + bi как точку с координатами (a,b).

Рисунки 37 и 38: комплексные числа

В викторианскую эпоху многие относились к мнимым числам с подозрением. Однако ирландский математик и астроном Уильям Роуэн Гамильтон покончил с этими сомнениями, определив комплексные числа применительно к кватернионам.

Самое красивое уравнение: тождество Эйлера

Тождество Эйлера связывает экспоненциальную функцию с функциями синуса и косинуса, значения которых колеблются от минус единицы до единицы. Чтобы найти связь с тригонометрическими функциями, мы можем представить их в виде бесконечного ряда, истинного для всех значений

Рисунок 40: тождество Эйлера

Эйлер никогда не записывал это тождество в явном виде, и мы не знаем, кто впервые записал его. Тем не менее, мы связываем его с именем Эйлера в знак почтения перед этим великим первопроходцем математики.

Pелятивистская квантовая механика. Уравнение Дирака

«На нем стоит большая часть физики и вся химия.»
Поль Дирак о своем уравнении

Вся классическая физика зиждется на том убеждении, что, зная закон движения частицы и факт появления ее в точке А, мы абсолютно точно можем предсказать, когда она попадет в точку В. Квантовая механика утверждает, что, зная закон движения микрочастицы и факт появления ее в точке А, мы можем определить всего лишь вероятность ее появления в точке В.

Вначале объясним слово «релятивистский». В физике под этим термином понимают все связанное с теорией относительности применительно к физическим эффектам, явлениям, наблюдаемым при скоростях тел или частиц, сравнимых со скоростью света. Так, к примеру, релятивистская частица—это частица, движущаяся с релятивистской скоростью, то есть близкой к скорости света.

А все началось с игры

В 1928 году английский физик Поль Дирак вывел уравнение движения для классического поля электрона, являющегося релятивистской частицей. Позднее оно было применено и для описания других фермионов. Однако по порядку.

Сам Дирак вспоминал, что начал работать над своей релятивистской теорией, «играясь с уравнениями, а не пытаясь ввести какую-нибудь определенную физическую идею». В чем же состояла эта игра Дирака?

Он хотел найти такое уравнение, которое, во-первых, было бы релятивистским, то есть удовлетворяло принципам теории относительности, во-вторых, подчинялось бы требованиям теории преобразований и, в-третьих, было бы квантово-механическим уравнением, описывающим движение электрона.

Но что значит «релятивистское уравнение»? Одним из характерных признаков такого уравнения является то, что в него должны входить как пространственные координаты х, у, z, так и временная координата t. Это уравнение должно быть квантово-механическим, то есть содержать волновую функцию электрона.

Дирак хотел просто привести в соответствие релятивистские принципы и требования теории преобразований. Оказалось, что существование спина как бы само собой возникает при объединении квантовой механики и теории относительности. Получилось, что квантовое уравнение, записанное с учетом требований теории относительности, описывает поведение частиц со спином.

Дираковская теория электрона наделяет электрон релятивистскими свойствами, а именно спином, то есть собственным механическим моментом количества движения и собственным магнитным моментом.

Релятивистский — термин, употребляемый в физике для явлений, обусловленных движением со скоростями, близкими к скорости света, либо сильными полями тяготения. Такие явления описываются теорией относительности.

Теория, порождающая загадки

Уравнение Дирака дало возможность получить более точную формулу для уровней энергии атома водорода. Но особенностью его уравнения было наличие среди его решений таких, которые соответствуют состояниям с отрицательными значениями энергии для свободного движения частицы, а это уже соответствует отрицательной массе частицы. Это означало, что все механические законы для частицы в таких состояниях были бы неверными, переходы же в квантовой теории в эти состояния возможны. Действительный физический смысл переходов на уровни с отрицательной энергией выяснился, когда была доказана возможность взаимопревращения частиц. Из уравнения Дирака следовало, что должна существовать новая частица—античастица по отношению к электрону, с массой электрона и зарядом противоположного знака. Такая частица была открыта в 1932 году американским физиком-экспериментатором Карлом Андерсоном и получила название «позитрон». Переход электрона из состояния с отрицательной энергией в состояние с положительной энергией и обратный переход рассматриваются как процесс образования пары электрон — позитрон и аннигиляция, то есть взаимное уничтожение такой пары.

Однако, несмотря на эти успехи, теория Дирака имеет и недостаток. Она не описывает взаимодействие квантованного электронного поля с квантованным электромагнитным полем, в том числе и рождение или уничтожение частиц. Эта трудность была разрешена в квантовой теории поля. В случае с электронами следует добавить квантованное электромагнитное поле, квантование самого электронного поля и взаимодействие этих полей, а полученная теория уже называется квантовой электродинамикой.

«. Квантовую электродинамику можно уложить в рамки разумной математической теории, но лишь ценой нарушения релятивистской инвариантности. Мне, однако, это кажется меньшим злом, чем отступление от стандартных правил математики и пренебрежение бесконечными величинами» (Поль Дирак)