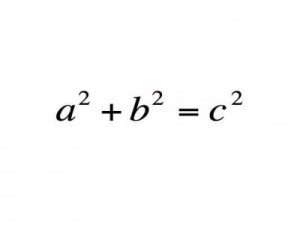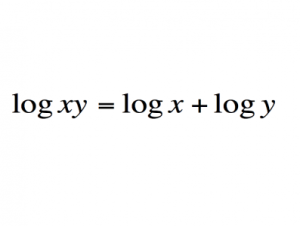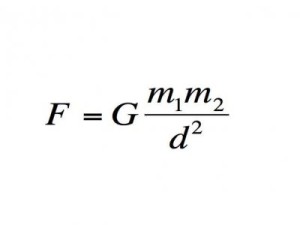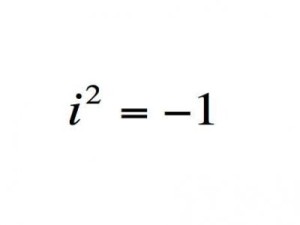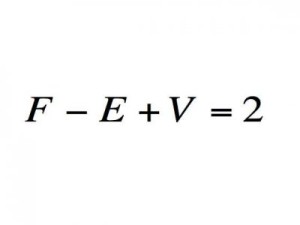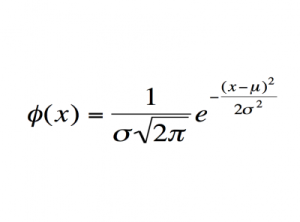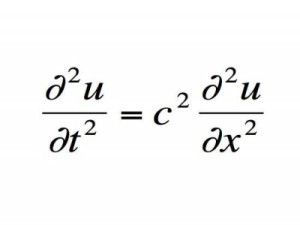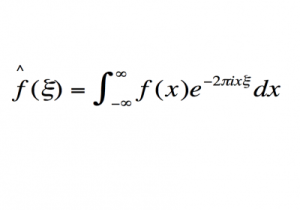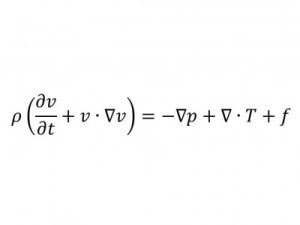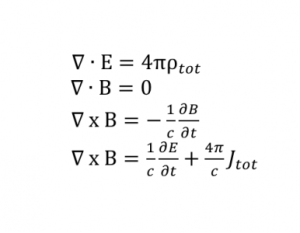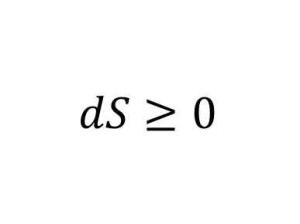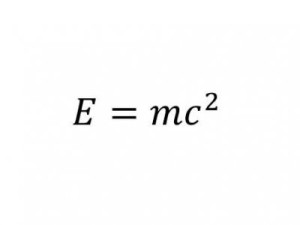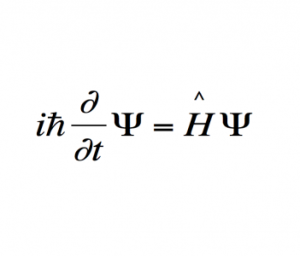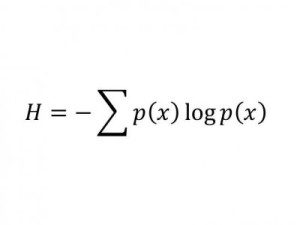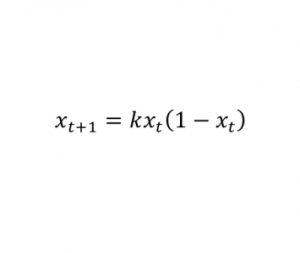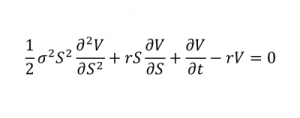Самые сложные уравнения в мире

7 математических загадок тысячелетия. Просто о сложном

Только для мыслящих людей!

«Я знаю только то, что ничего не знаю, но другие не знают и этого»
(Сократ, древнегреческий философ)

НИКОМУ не дано владеть вселенским разумом и знать ВСЁ. Тем не менее, у большинства ученых, да и тех, кто просто любит размышлять и исследовать, всегда есть стремление узнать больше, разгадать загадки. Но остались ли еще неразгаданные темы у человечества? Ведь, кажется, все уже ясно и нужно только применять полученные веками знания?

НЕ стоит отчаиваться! Еще остались нерешенные проблемы из области математики, логики, которые в 2000 году эксперты Математического института Клэя в Кембридже (Массачусетс, США) объединили в список, так называемые, 7 загадок тысячелетия (Millennium Prize Problems). Эти проблемы волнуют ученых всей планеты. С тех пор и по сей день любой человек может заявить, что нашел решение одной из задач, доказать гипотезу и получить от бостонского миллиардера Лэндона Клэя (в честь которого и назван институт) премию. Он уже выделил на эти цели 7 миллионов долларов. К слову сказать, на сегодняшний день одна из проблем уже решена.

Итак, вы готовы узнать о математических загадках?

Уравнения Навье — Стокса (сформулированы в 1822 году)

Уравнения о турбулентных, воздушных потоках, а также течении жидкостей известны как уравнения Навье — Стокса. Если, к примеру, плыть по озеру на чем-либо, то неизбежно вокруг возникнут волны. Это касается и воздушного пространства: при полете на самолете в воздухе также будут образовываться турбулентные потоки.
Данные уравнения как раз производят описание процессов движения вязкой жидкости и являются стержневой задачей всей гидродинамики. Для некоторых частных случаев уже найдены решения, в которых части уравнений отбрасываются, как не влияющие на конечный результат, но в общем виде решения этих уравнений не найдены.
Необходимо найти решение уравнениям и выявить гладкие функции.

Гипотеза Римана (сформулирована в 1859 году)

Область: теория чисел

Известно, что распределение простых чисел (Которые делятся только на себя и на единицу: 2,3,5,7,11…) среди всех натуральных чисел не подчиняется никакой закономерности.
Над этой проблемой задумался немецкий математик Риман, который сделал свое предположение, теоретически касающееся свойств имеющейся последовательности простых чисел. Уже давно известны так называемые парные простые числа — простые числа-близнецы, разность между которыми равна 2, например 11 и 13, 29 и 31, 59 и 61. Иногда они образуют целые скопления, например, 101, 103, 107, 109 и 113.
Если такие скопления будут найдены и выведен определенный алгоритм, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.

Проблема Пуанкаре (сформулирована в 1904 году. Решена в 2002 году.)

Область: топология или геометрия многомерных пространств

Суть проблемы заключается в топологии и состоит в том, что если натягивать резиновую ленту, к примеру, на яблоко (сферу), то будет теоретически возможным сжать ее до точки, медленно перемещая без отрыва от поверхности ленту. Однако если эту же ленту натянуть вокруг бублика (тора), то сжать ленту без разрыва ленты или разлома самого бублика не представляется возможным. Т.е. вся поверхность сферы односвязна, в то время как тора – нет. Задача состояла в том, чтобы доказать, что односвязной является только сфера.

Представитель ленинградской геометрической школы Григорий Яковлевич Перельман является лауреатом премии тысячелетия математического института Клэя (2010 г.) за решение проблемы Пуанкаре. От знаменитой Фильдсовской премии он отказался.

Гипотеза Ходжа (сформулирована в 1941 году)

Область: алгебраическая геометрия

В реальности существуют множество как простых, так и куда более сложных геометрических объектов. Чем сложнее объект, тем труднее его изучать. Сейчас учеными придуман и вовсю применяется подход, основанный на использовании частей одного целого («кирпичики») для изучения этого объекта, как пример — конструктор. Зная свойства «кирпичиков», становится возможным подступиться и к свойствам самого объекта. Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков», так и объектов.
Это очень серьезная проблема алгебраической геометрии: найти точные пути и методы анализа сложных объектов с помощью простых «кирпичиков».

Уравнения Янга — Миллса (сформулированы в 1954 году)

Область: геометрия и квантовая физика

Физики Янг и Миллс описывают мир элементарных частиц. Они, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения в области квантовой физики. Тем самым был найден путь к объединению теорий электромагнитного, слабого и сильного взаимодействий.
На уровне микрочастиц возникает «неприятный» эффект: если на частицу действуют несколько полей сразу, их совокупный эффект уже нельзя разложить на действие каждого из них поодиночке. Это происходит по причине того, что в этой теории друг к другу притягиваются не только частицы материи, но и сами силовые линии поля.
Хотя и уравнения Янга — Миллса приняты всеми физиками мира, экспериментально теория, касающаяся предсказывания массы элементарных частиц, не доказана.

Гипотеза Берча и Свиннертон-Дайера (сформулирована в 1960 году)

Область: алгебра и теория чисел

Гипотеза связана с уравнениями эллиптических кривых и множеством их рациональных решений. В доказательстве теоремы Ферма эллиптические кривые заняли одно из важнейших мест. А в криптографии они образуют целый раздел имени себя, и на них основаны некоторые российские стандарты цифровой подписи.
Задача в том, что нужно описать ВСЕ решения в целых числах x, y, z алгебраических уравнений, то есть уравнений от нескольких переменных с целыми коэффициентами.

Проблема Кука (сформулирована в 1971 году)

Область: математическая логика и кибернетика

Ее еще называют «Равенство классов P и NP», и она является одной из наиболее важных задач теории алгоритмов, логики и информатики.
Может ли процесс проверки правильности решения какой-либо задачи длиться дольше, чем время, затраченное на само решение этой задачи (независимо от алгоритма проверки)?
На решение одной и той же задачи, порой, нужно разное количество времени, если изменить условия и алгоритмы. К примеру: в большой компании вы ищете знакомого. Если вы знаете, что он сидит в углу или за столиком — то вам понадобится доли секунд, чтобы его увидеть. Но если вы не будете знать точно, где находится объект, то затратите больше времени на его поиски, обходя всех гостей.
Основным вопросом является: все или не все задачи, которые можно легко и быстро проверить, можно также легко и быстро решить?

Математика, как может показаться многим, не так далека от реальности. Она является тем механизмом, с помощью которого можно описать наш мир и многие явления. Математика всюду. И прав был В.О. Ключевский, который изрек: «Не цветы виноваты, что слепой их не видит».

Уравнение Шрёдингера

Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.

Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.

Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.

Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):

где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.

Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.

Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.

Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).

Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.

Формулы и уравнения, которые изменили мир

Математик Ян Стюарт (Ian Stewart) в своей новой книге «В поисках неизвестного: 17 уравнений, которые изменили мир» рассматривает несколько наиболее важных уравнений всех времен и приводит примеры их практического применения.

Теорема Пифагора

Согласно Теореме Пифагора в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Важность: Теорема Пифагора — важнейшее уравнение в геометрии, которое связывает ее с алгеброй и является основой тригонометрии. Без него было бы невозможно создать точную картографию и навигацию.

Современное использование: Триангуляция используется и по сей день, чтобы точно определить относительное расположение для GPS навигации.

Логарифм и его тождество

Логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент.

Важность: Логарифмы стали настоящей революцией, позволив астрономам и инженерам делать расчеты более быстро и точно. С появлением компьютеров они не потеряли своего значения, поскольку все еще существенны для ученых.

Современное использование: Логарифмы важная составляющая для понимания радиоактивного распада.

Основная теорема анализа

Основная теорема анализа или формула Ньютона — Лейбница дает соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.

Важность: Теорема анализа фактически создала современный мир. Исчисление имеет важное значение в нашем понимание того, как измерять тела, кривые и площади. Она является основой многих природных законов и источником дифференциальных уравнений.

Современное использование: Любая математическая проблема, где требуется оптимальное решение. Существенное значение для медицины, экономики и информатики.

Классическая теория тяготения Ньютона

Классическая теория тяготения Ньютона описывает гравитационное взаимодействие.

Важность: Теория позволяет рассчитать силу гравитации между двумя объектами. Хотя позднее она была вытеснена теорией относительности Эйнштейна, теория все равно необходима для практического описания того, как объекты взаимодействуют друг с другом. Мы используем ее и по сей день для проектирования орбит спутников и космических аппаратов.

Современное использование: Позволяет найти наиболее энергоэффективные пути для вывода спутников и космических зондов. Также делает возможным спутниковое телевидение.

Комплексные числа

Комплексные числа — расширение поля вещественных чисел.

Важность: Многие современные технологии, в том числе цифровые фотокамеры, не могли быть изобретены без комплексных чисел. Кроме того, они позволяют проводить анализ, который нужен инженерам для решения практических задач в авиации.

Современное использование: Широко используется в электротехнике и сложных математических теориях.

Эйлерова характеристика полиэдров

Важность: Внесла вклад в понимание топологического пространства, в котором рассматриваются только свойства непрерывности. Необходимый инструмент для инженеров и биологов.

Современное использование: Топология используется, чтобы понять поведение и функции ДНК.

Нормальное распределение

Важность: Уравнение является основой современной статистики. Естественные и социальные науки не могли бы существовать в своей нынешней форме без него.

Современное использование: Используется в клинических испытаниях для определения эффективности лекарств по сравнению с отрицательными побочными эффектами.

Волновое уравнение

Дифференциальное уравнение, описывающее поведение волн.

Важность: Волны исследуются с целью определения времени и места землетрясений, а также для прогнозирования поведения океана.

Современное использование: Нефтяные компании используют взрывчатку, а затем считывают данные от последующих звуковых волн для определения геологических формаций.

Преобразование Фурье

Важность: Уравнение позволяет разбивать, очищать и анализировать сложные шаблоны.

Современное использование: Используется при сжатии информации изображений в формате JPEG, а так же для обнаружения структуры молекул.

Уравнения Навье—Стокса

В левой части уравнения — ускорение небольшого количества жидкости, в правой — силы, которые воздействуют на него.

Важность: Как только компьютеры стали достаточно мощными, чтобы решить это уравнение, они открыли сложную и очень полезную области физики. Она особенно полезна для создания более качественной аэродинамики у транспортных средств.

Современное использование: Среди прочего, уравнение помогло в усовершенствовании современных пассажирских самолетов.

Уравнения Максвелла

Описывают электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Важность: Помогли в понимании электромагнитных волн, что способствовало созданию многих технологий, которые мы используем сегодня.

Современное использование: Радар, телевидение и современные средства связи.

Второй закон термодинамики

Вся энергия и тепло со временем исчезнет.

Важность: Имеет существенное значение для нашего понимания энергии и Вселенной через понятие энтропии. Открытие закона помогло улучшить паровой двигатель.

Современное использование: Помог доказать, что материя состоит из атомов, физики до сих пор пользуются этим знанием.

Теория относительности Эйнштейна

Энергия равна массе, умноженной на квадрат скорости света.

Важность: Наверное, самое известное уравнение в истории. Оно полностью изменило нашу точку зрения на материю и реальность.

Современное использование: Помогло создать ядерное оружие. Используется в GPS навигации.

Уравнение Шрёдингера

Нелинейное уравнение Шрёдингера

Описывает материю как волну, а не как частицу.

Важность: Перевернула представления физиков — частицы могут существовать в диапазоне возможных состояний.

Современное использование: Существенный вклад в использование полупроводников и транзисторов, и, таким образом, в большинство современных компьютерных технологий.

Информационная энтропия Шаннона

Оценивает количество данных в куске кода путем расчета вероятности его символов.

Важность: Это уравнение, которое открыло дверь в Информационную Эпоху.

Современное использование: В значительной степени все, что связано с обнаружением ошибок в кодировании (программировании).

Логистическая модель роста популяций

Оценка изменений в популяции живых существ из поколения в поколение с ограниченными ресурсами.

Важность: Помогла в развитии теории хаоса, которая полностью изменила наше понимание того, как работают природные системы.

Современное использование: Используется для моделирования землетрясений и прогноза погоды.

Модель Блэка-Скоулза

Модель Блэка Скоулза

Одна из моделей ценообразования опционов.

Важность: Помогла создать несколько триллионов долларов. Согласно некоторым экспертам, неправильное использование формулы (и ее производных) способствовало финансовому кризису. В частности, уравнение имеет несколько предположений, которые не справедливы на реальных финансовых рынках.

Современное использование: Даже после кризиса используются для определения цен.

Вместо заключения

В мире существует множество других важных уравнений и формул, которые изменили судьбу человечества в целом и нашу личную жизнь в частности. Среди них, модель Ходжкина—Хаксли, Фильтр Калмана и, конечно, уравнение поисковой системы Google. Мы надеемся, что нам удалось показать насколько важна математика, и насколько бесценен ее вклад для всех людей.

источники:

http://elementy.ru/trefil/21/Uravnenie_Shryodingera

http://starmission.ru/theory/formuly-i-uravneniya-kotorye-izmenili-mir.html