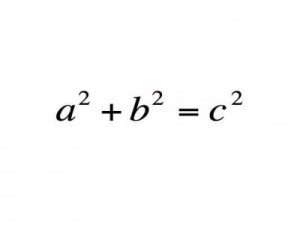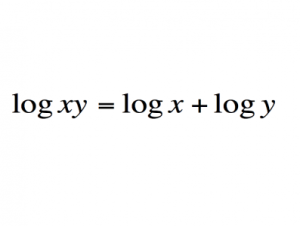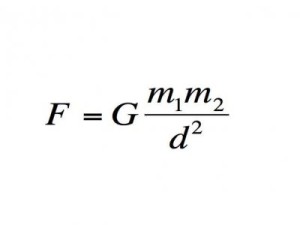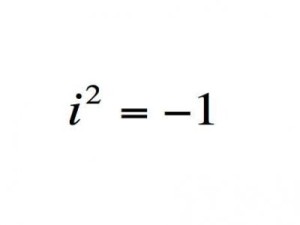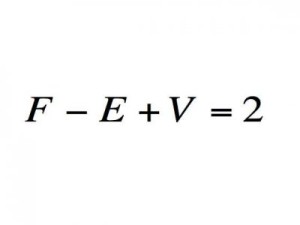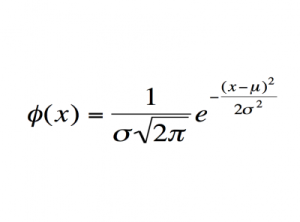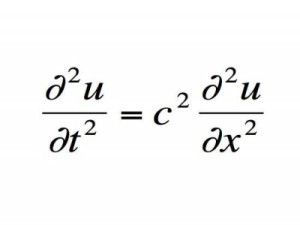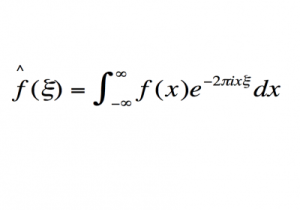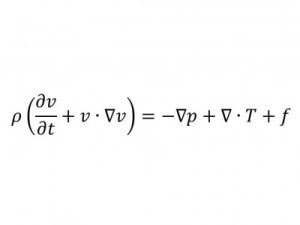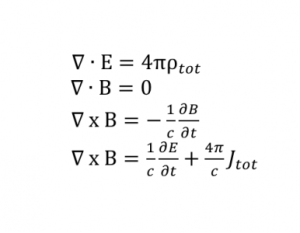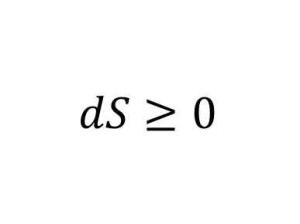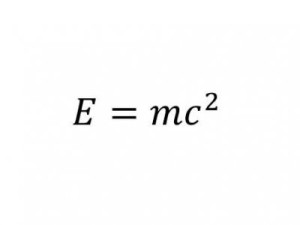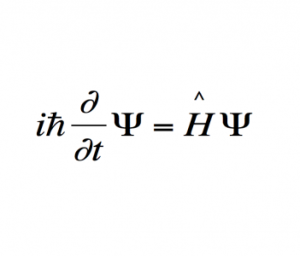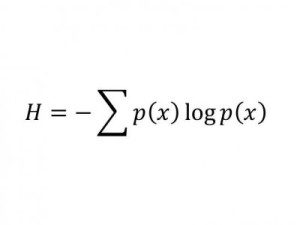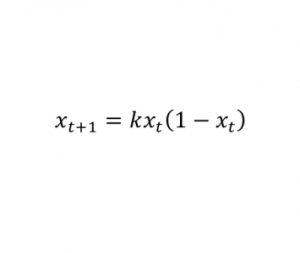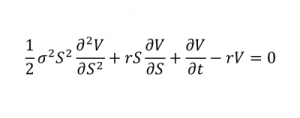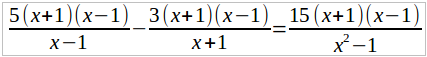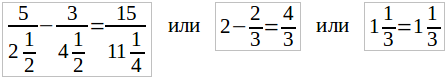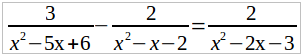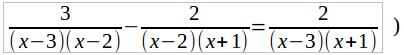Самый трудное уравнение в мире

Уравнение Шрёдингера

Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.

Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.

Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.

Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):

где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.

Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.

Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.

Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).

Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.

Формулы и уравнения, которые изменили мир

Математик Ян Стюарт (Ian Stewart) в своей новой книге «В поисках неизвестного: 17 уравнений, которые изменили мир» рассматривает несколько наиболее важных уравнений всех времен и приводит примеры их практического применения.

Теорема Пифагора

Согласно Теореме Пифагора в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Важность: Теорема Пифагора — важнейшее уравнение в геометрии, которое связывает ее с алгеброй и является основой тригонометрии. Без него было бы невозможно создать точную картографию и навигацию.

Современное использование: Триангуляция используется и по сей день, чтобы точно определить относительное расположение для GPS навигации.

Логарифм и его тождество

Логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент.

Важность: Логарифмы стали настоящей революцией, позволив астрономам и инженерам делать расчеты более быстро и точно. С появлением компьютеров они не потеряли своего значения, поскольку все еще существенны для ученых.

Современное использование: Логарифмы важная составляющая для понимания радиоактивного распада.

Основная теорема анализа

Основная теорема анализа или формула Ньютона — Лейбница дает соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.

Важность: Теорема анализа фактически создала современный мир. Исчисление имеет важное значение в нашем понимание того, как измерять тела, кривые и площади. Она является основой многих природных законов и источником дифференциальных уравнений.

Современное использование: Любая математическая проблема, где требуется оптимальное решение. Существенное значение для медицины, экономики и информатики.

Классическая теория тяготения Ньютона

Классическая теория тяготения Ньютона описывает гравитационное взаимодействие.

Важность: Теория позволяет рассчитать силу гравитации между двумя объектами. Хотя позднее она была вытеснена теорией относительности Эйнштейна, теория все равно необходима для практического описания того, как объекты взаимодействуют друг с другом. Мы используем ее и по сей день для проектирования орбит спутников и космических аппаратов.

Современное использование: Позволяет найти наиболее энергоэффективные пути для вывода спутников и космических зондов. Также делает возможным спутниковое телевидение.

Комплексные числа

Комплексные числа — расширение поля вещественных чисел.

Важность: Многие современные технологии, в том числе цифровые фотокамеры, не могли быть изобретены без комплексных чисел. Кроме того, они позволяют проводить анализ, который нужен инженерам для решения практических задач в авиации.

Современное использование: Широко используется в электротехнике и сложных математических теориях.

Эйлерова характеристика полиэдров

Важность: Внесла вклад в понимание топологического пространства, в котором рассматриваются только свойства непрерывности. Необходимый инструмент для инженеров и биологов.

Современное использование: Топология используется, чтобы понять поведение и функции ДНК.

Нормальное распределение

Важность: Уравнение является основой современной статистики. Естественные и социальные науки не могли бы существовать в своей нынешней форме без него.

Современное использование: Используется в клинических испытаниях для определения эффективности лекарств по сравнению с отрицательными побочными эффектами.

Волновое уравнение

Дифференциальное уравнение, описывающее поведение волн.

Важность: Волны исследуются с целью определения времени и места землетрясений, а также для прогнозирования поведения океана.

Современное использование: Нефтяные компании используют взрывчатку, а затем считывают данные от последующих звуковых волн для определения геологических формаций.

Преобразование Фурье

Важность: Уравнение позволяет разбивать, очищать и анализировать сложные шаблоны.

Современное использование: Используется при сжатии информации изображений в формате JPEG, а так же для обнаружения структуры молекул.

Уравнения Навье—Стокса

В левой части уравнения — ускорение небольшого количества жидкости, в правой — силы, которые воздействуют на него.

Важность: Как только компьютеры стали достаточно мощными, чтобы решить это уравнение, они открыли сложную и очень полезную области физики. Она особенно полезна для создания более качественной аэродинамики у транспортных средств.

Современное использование: Среди прочего, уравнение помогло в усовершенствовании современных пассажирских самолетов.

Уравнения Максвелла

Описывают электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Важность: Помогли в понимании электромагнитных волн, что способствовало созданию многих технологий, которые мы используем сегодня.

Современное использование: Радар, телевидение и современные средства связи.

Второй закон термодинамики

Вся энергия и тепло со временем исчезнет.

Важность: Имеет существенное значение для нашего понимания энергии и Вселенной через понятие энтропии. Открытие закона помогло улучшить паровой двигатель.

Современное использование: Помог доказать, что материя состоит из атомов, физики до сих пор пользуются этим знанием.

Теория относительности Эйнштейна

Энергия равна массе, умноженной на квадрат скорости света.

Важность: Наверное, самое известное уравнение в истории. Оно полностью изменило нашу точку зрения на материю и реальность.

Современное использование: Помогло создать ядерное оружие. Используется в GPS навигации.

Уравнение Шрёдингера

Нелинейное уравнение Шрёдингера

Описывает материю как волну, а не как частицу.

Важность: Перевернула представления физиков — частицы могут существовать в диапазоне возможных состояний.

Современное использование: Существенный вклад в использование полупроводников и транзисторов, и, таким образом, в большинство современных компьютерных технологий.

Информационная энтропия Шаннона

Оценивает количество данных в куске кода путем расчета вероятности его символов.

Важность: Это уравнение, которое открыло дверь в Информационную Эпоху.

Современное использование: В значительной степени все, что связано с обнаружением ошибок в кодировании (программировании).

Логистическая модель роста популяций

Оценка изменений в популяции живых существ из поколения в поколение с ограниченными ресурсами.

Важность: Помогла в развитии теории хаоса, которая полностью изменила наше понимание того, как работают природные системы.

Современное использование: Используется для моделирования землетрясений и прогноза погоды.

Модель Блэка-Скоулза

Модель Блэка Скоулза

Одна из моделей ценообразования опционов.

Важность: Помогла создать несколько триллионов долларов. Согласно некоторым экспертам, неправильное использование формулы (и ее производных) способствовало финансовому кризису. В частности, уравнение имеет несколько предположений, которые не справедливы на реальных финансовых рынках.

Современное использование: Даже после кризиса используются для определения цен.

Вместо заключения

В мире существует множество других важных уравнений и формул, которые изменили судьбу человечества в целом и нашу личную жизнь в частности. Среди них, модель Ходжкина—Хаксли, Фильтр Калмана и, конечно, уравнение поисковой системы Google. Мы надеемся, что нам удалось показать насколько важна математика, и насколько бесценен ее вклад для всех людей.

Математика

52. Более сложные примеры уравнений.
Пример 1 .

5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)

Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

5x + 5 – 3x + 3 = 15

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x 2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

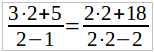
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.

Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

3x + 3 – 2x + 6 = x – 2

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

источники:

http://starmission.ru/theory/formuly-i-uravneniya-kotorye-izmenili-mir.html

http://maths-public.ru/algebra1/equations-examples