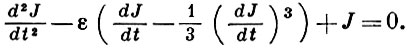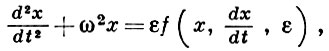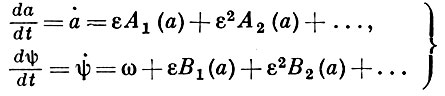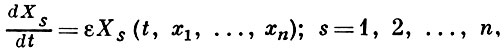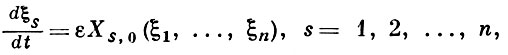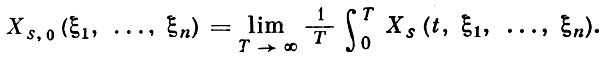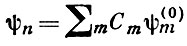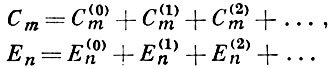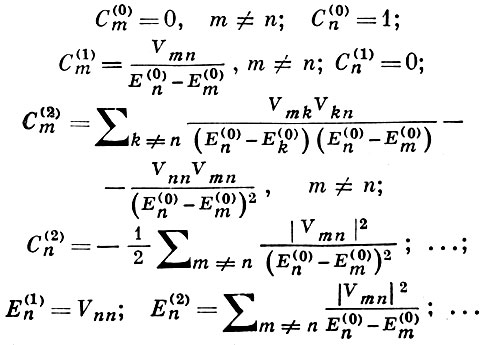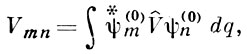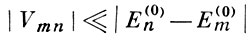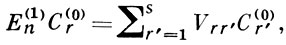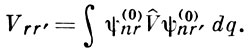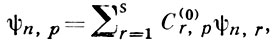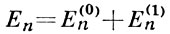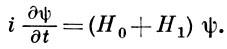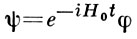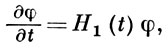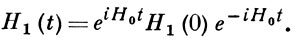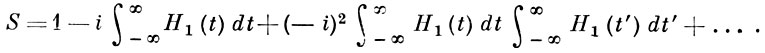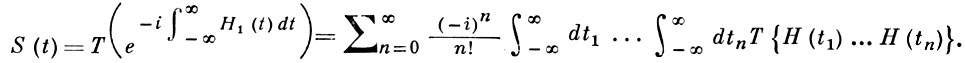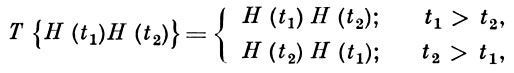Секулярное уравнение в квантовой механике

Методы квантовой механики

Вы будете перенаправлены на Автор24

Квантовая механика занимается описанием главных свойств и поведения конденсированных сред, молекул, ионов, атомов, а также иных систем, имеющих электронно-ядерное строение. Более точным инвариантным описанием превращений элементарных частиц занимается квантовая теория поля. Эксперименты дают подтверждение результатам, полученным с помощью квантовой механики.

Квантовая механика представляет раздел теоретической физики, который описывает физические явления, где действие равнозначно по величине постоянной Планка. Законы квантовой механики существенно отличаются от классической. В квантовой механике применяются следующие основные методы:

• приближенные (квазиклассическое приближение и теория возмущений);
• резонансные (метод резонанса).

Метод квазиклассического приближения

Квазиклассическое приближение известно в физике также как метод Крамерса – Вентцеля — Бриллюэна). Данный метод представляет наиболее известный в квантовой механике пример квазиклассического вычисления, волновая функция в котором изначально представлена как показательная и квазиклассически расширенная с последующим постепенным изменением амплитуды или фазы.

Название метод получил, благодаря физикам Г. Вентцелю, Х. Крамерсу и Л. Бриллюэну, предложившим его в 1926 году. В 1923 г. Г. Джеффри развивает общий метод приближенного решения для линейных дифференциальных уравнений 2-го порядка. Он включил в себя и решение уравнения Шредингера.

Одномерное стационарное уравнение Шредингера:

Также можно записать в виде:

Готовые работы на аналогичную тему

Если представить волновую функцию как экспоненциальную другой неизвестной функции $Φ$:

Тогда $Ф$ должна будет удовлетворять следующему уравнению:

здесь $Ф’$ означает производную от $Ф$ по $x$. Разделим $\Phi ‘(x)$ на действительную часть и мнимую при вводе функций $A$ и $B$:

Для решения этих уравнений нам нужно рассмотреть квазиклассическое приближение. Это означает разложение каждой из функций как ряд по степеням $\bar$. Уравнения показывают, что степенной ряд должен начинаться с $\bar^<-1>$ для удовлетворения реальной части уравнения. Но поскольку нам требуется хороший классический предел, то разложение нужно начинать с максимально высокой степени постоянной Планка. Эта степень должна быть настолько высокой, насколько это действительно возможно.

Таким образом, уравнения с точностью до первого порядка разложения запишутся в виде

Метод теории возмущений

Теория возмущений представляет метод приближенного решения задач в теоретической физике. Его применение актуально только в случае, если в задаче будет присутствовать малый параметр. При этом в пренебрежении данным параметром задача будет иметь точное решение.

Рассчитанные на основе теории возмущений физические величины, будут иметь вид ряда: $A=A^(0)+\varepsilon A^(1)+\varepsilon^2A^(2)+. $

где $A^(0)$ будет решением невозмущенной задачи; $\varepsilon$ это малый параметр.

Коэффициенты $A^(n)$ мы находим посредством последовательных приближений. Другими словами, $A^(n)$ будет выражаться через $A^(0), A^(n-1)$. Использование метода теории возмущений актуально для:

• небесной механики;
• квантовой теории поля;
• квантовой механики.

В квантовой механике метод теории возмущений применяется тогда, когда гамильтониан системы возможно представить в таком виде:

где $H^(0)$ будет не возмущенным гамильтонианом (при этом решение соответствующего уравнения Шрёдингера точно известно), а $V$ — добавкой (возмущением).

Метод резонанса

Автором непосредственной идеи резонанса выступил Вернер Гейзенберг, который предложил ввести это понятие в квантовую механику. Об этом физик заявил в 1926 году во время обсуждения квантовых состояний атома гелия. Ученый предложил сравнение структуры атома гелия и классической системы резонирующего гармонического осциллятора.

Модель Гейзенберга решил применить Лайнус Полинг в 1928 году. Он использовал ее с целью описания электронной структуры молекул. Полингу, задействуя метод валентных схем, удалось успешно объяснить геометрические, а также физико-химические свойства целого ряда молекул. Для этого физик применял механизм делокализации электронной плотности $\pi$ связей.

Аналогичные идеи с целью описания самой электронной структуры ароматических соединений предложил Кристофер Ингольд. В период с 1926 по 1934 гг. ученый развивает альтернативную теорию электронных смещений. Она получила название теории мезомерии. Ее принципы базировались на объяснении структуры молекул в сложных органических соединениях, которое не укладывалось в стандартные валентные представления.

Сам термин «мезомеризм», предложенный К. Ингольдом для обозначения такого явления, как делокализация электронной плотности, в 1938 году, применяется преимущественно во французской и немецкой научной литературе, в русской и английской преобладает «резонанс».

Представления ученого о мезомерном эффекте стали неотъемлемой частью теории резонанса. Благодаря работам немецкого ученого Фрица Арндта, были введены обозначения мезомерных структур с помощью двунаправленных стрелок, впоследствии ставшие общепринятыми.

ВОЗМУЩЕНИЙ ТЕОРИЯ

ВОЗМУЩЕНИЙ ТЕОРИЯ — комплекс методов исследования различных задач, используемый во многих разделах математики, механики, физики и техники. Здесь с общей точки зрения излагаются основные идеи В. т.

B. т. основана на возможности приближенного описания исследуемой системы с помощью нек-рой специальным образом выбираемой «идеальной» системы, допускающей корректное и полное изучение. Одним из признаков применимости В. т. в одной из ее форм, определяемой спецификой конкретной задачи, для к-рой В. т. разрабатывается, является условие того, что уравнения, описывающие исследуемый процесс, содержат в явной или неявной форме малый параметр (или несколько таких параметров). При этом требуется, чтобы при нулевом значении малого параметра уравнения допускали точное решение, и таким образом проблема сводится к нахождению асимптотики наилучшего приближения к истинному решению с точностью до ε, ε 2 , . .

1) В. т. впервые была предложена для решения проблем небесной механики, связанных с изучением движения планет в солнечной системе. Удаленность планет друг от друга и малая величина их массы в сравнении с массой Солнца позволяют пренебрегать гравитационным взаимодействием планет между собой и рассматривать их движение (в первом приближении) по орбитам Кеплера, определяемым из уравнений двух тел задачи — планеты и Солнца.

Существенное уточнение астрономич. данных сформулировало проблему учета влияния других планет на движение одной из них вокруг Солнца. Так возникла классическая трех тел задача, причем, напр., при изучении системы Луна — Земля — Солнце в качестве малого параметра выбиралось отношение масс Луны и Земли. Начиная с трудов Ж. Лагранжа (J. Lagrange), П. Лапласа (P. Laplace) было выдвинуто представление о том, что постоянные величины, характеризующие движение планеты вокруг Солнца, ввиду влияния движения других планет как бы «возмущаются» и претерпевают изменения, зависящие от времени; отсюда идет и наименование «теория возмущений».

В. т. занимала внимание классиков Ж. Лагранжа, П. Лапласа, С. Пуассона (S. Poisson), К. Гаусса (С. Gauss) и в результате их работ оказалось возможным проводить вычисления с чрезвычайно большой точностью. Триумфом В. т. явилось открытие планеты Нептун (1848) Дж. Адамсом (J. Adams) и У. Леверье (U. Le Verrier) из анализа отклонений в движении планеты Уран.

Трудности первоначально разработанных методов В. т. были обусловлены наличием в получающихся разложениях членов, содержащих время t вне знака синуса или косинуса. Вклад таких членов в ряд В. т. существен лишь за длительные промежутки времени (порядка столетий), но и в этом случае невозможно строгое описание планетных движений в схеме В. т.- приемлемым является только первое приближение. Появление так наз. секулярных членов обусловлено зависимостью частоты движения (обращения) исследуемой планеты от соответствующих частот других планет. Учет такого рода зависимости и приводит к возникновению в решениях как секулярных (вида At n ), так и смешанных (вида Bt cos (ωt + φ)) членов. Напр., соотношение

в схеме В. т. допускает следующее разложение по ε (ε〈〈1):

смешанный член в к-ром появляется в результате разложения колебания с частотой (1) по колебаниям с частотой ω₀.

Создание специальных методов В. т., устраняющих секулярные члены, т. е. позволяющих представить решение в чисто тригонометрич. виде, связано с работами Линдштедта (Lindstedt), П. Гульдина (P. Guldin), Ш.Делоне (Ch. Delaunay), Б. Волина (В. Bohlin), С. Ньюкома (S. Newcomb). В предложенном ими подходе частоты уже не разлагаются по малым параметрам, т. е. в соответствующие разложения входят не частоты нулевого приближения, а нек-рым образом переопределенные (в терминах современной теоретич. физики — ренормированные) частоты. В результате каждый отдельный член ряда В. т. но Степеням малого параметра представляет собой сходящееся выражение. Вопрос о сходимости ряда В. т. в целом остается открытым из-за появления так наз. малых знаменателей (малых делителей), образующихся при интегрировании в каждом приближении В. т. выражений вида expjω_jn_it + φ>, где <ω_j> — набор частот, отвечающих различным движениям. В случае почти соизмеримых частот сумма в показателе экспоненты может быть малой и тогда после соответствующего интегрирования возникают члены ряда В. т., знаменатели к-рых малы, что и приводит к расходящимся выражениям ряда В. т. В частности, для двух частот ω₁ и ω₂, отношение к-рых является иррациональным числом, (n₁ω₁ + n₂ω₂) можно подобрать так, чтобы соответствующий ряд В. т. расходился.

При изучении с общей математич. точки зрения проблемы малых знаменателей А. Пуанкаре (Н. Poincaré) и А. М. Ляпуновым была предложена методика построения специального вида периодич. решений, эффективная не только в задачах небесной механики, но и в теории дифференциальных уравнений в целом.

Существенный вклад в решение проблемы малых делителей был сделан в работах [4], [5], [6]. Метод последовательных канонич. замен переменных позволяет «понизить» порядок возмущения и с помощью достигаемой усиленной сходимости (так наз. сверхсходимости) «преодолеть» расходимость ряда В. т. из-за малых знаменателей, возникающих в каждом порядке В. т., надлежащим выбором канонич. преобразования.

2) В В. т. для задач небесной механики развито асимптотич. интегрирование дифференциальных уравнений только в случае консервативных систем. Дальнейший прогресс В. т. связан с развитием теории колебаний, в особенности с созданием теории нелинейных колебаний.

Важную роль сыграли (выполненные в развитие работ Ж.Лагранжа) исследования Б. Ван дер Поля (В. Van der Pol) по уравнениям типа Рэлея с малым параметром ε:

Частным случаем уравнения (3) является Ван дер Поля уравнение.

Для решения уравнения

ẍ — ε(1 — ẋ 2 )ẋ + ω 2 х = 0 (4)

в первом приближении Б. Ван дер Поль предложил без должного математич. обоснования метод «медленно меняющихся коэффициентов», аналогичный одному из методов, применявшихся еще Ж. Лагранжем в небесной механике. Этот метод основан на представлении решения уравнения (4) в виде функции гармония, колебаний, амплитуда и фаза к-рых — медленно меняющиеся функции параметра t.

Общая теория нелинейных колебаний была разработана в работах Н. М. Крылова и Н. Н. Боголюбова. При этом были преодолены принципиальные математич. трудности и дано распространение В. т. на общие неконсервативные системы. Развитые в этих работах новые асимптотич. методы нелинейной механики позволяют получать решения в высших приближениях В. т. в математически обоснованной схеме, причем наряду с периодич. решениями допускали строгое рассмотрение квазипериодич. режима.

Идея асимптотич. методов теории возмущений Крылова-Боголюбова становится наглядной при рассмотрении уравнения

описывающего нелинейные колебания системы с одной степенью свободы.

К правильной формулировке асимптотич. метода можно прийти, исходя из физич. соображений о характере колебательного процесса. Так, при полном отсутствии нелинейности, т. е. при ε = 0, колебания, описываемые уравнением (5), будут чисто гармоническими с постоянной амплитудой и равномерно вращающейся фазой. В случае, если ε ≠ 0, т. е. в случае наличия нелинейного возмущения, естественно ожидать появления в решении уравнения (5) обертонов, зависимости мгновенной частоты от амплитуды и, наконец, систематич. увеличения или уменьшения амплитуды колебания в связи с притоком или поглощением энергии возмущающими силами.

Принимая во внимание все эти физич. соображения, естественно решение уравнения (5) искать в виде ряда

х = а cos ψ + εu₁(a, ψ) + ε 2 u₂(a, ψ)+ . (6)

в к-ром u_i(a, ψ), i = 1, 2, . — периодич. функции угла ψ с периодом 2π, а величины а и ψ как функции времени определяются дифференциальными уравнениями

Таким образом, задача сводится к подбору соответствующих выражений для функций u_i(a, ψ), A_i(а), В_i(а), i = 1, 2, . так, чтобы выражение (6), в к-рое вместо а и ψ будут подставлены функции времени, определенные из системы (7), являлось решением исходного уравнения (5). Причем накладываются нек-рые дополнительные условия, обеспечивающие отсутствие в решении (6) секулярных членов.

Ограничиваясь в формальном ряде (6) первыми членами, приходят к m-му приближению, обладающему свойством асимптотичности в том смысле, что при фиксированном m и ε → 0 выражение (6) стремится к точному решению уравнения (5); уравнения первого приближения совпадают с уравнениями Ван дер Поля. Проблема оценки погрешности m-го приближения не вызывает особенных трудностей. Аналогичным образом решается задача в случае N степеней свободы.

Если интерпретировать формулу (6) не как решение уравнения (5), а как формулу замены переменных, то можно получить точные выражения для производных по времени от амплитуды а и фазы ψ.

Как известно (см. [8], [9]) во многих случаях дифференциальные уравнения, описывающие колебательные процессы и содержащие «малый» параметр, могут быть приведены к так наз. стандартной форме:

где ε — малый положительный параметр. Большое число задач физики и техники приводится к этому виду. Для системы дифференциальных уравнений вида (8) разработан особый метод аппроксимации, названный методом усреднения. Согласно методу усреднений, эти уравнения для достаточно малых значений ε на конечном интервале посредством замены переменных

приводятся к усредненным уравнениям:

Применяя метод усреднения, можно получить, напр., ряд критериев о существовании и устойчивости автоколебательных режимов.

Были установлены [13] при весьма общих условиях оценки разности |X_i — ε_i| на временном интервале длины L/ε. Кроме того, можно установить соответствие и в таких свойствах решений общих систем, к-рые зависят от их поведения на бесконечном интервале. Таким образом были доказаны теоремы о существовании и устойчивости квазипериоднч. решений.

3) При изучении нелинейных колебательных систем можно не приводить соответствующую систему уравнений к «стандартной форме», а работать непосредственно с исходными дифференциальными уравнениями для системы гармонич. вибраторов, подверженных слабому нелинейному воздействию. При этом наряду с общими решениями для такой системы можно получить и частные решения с помощью замены переменных специального вида.

Такой подход был использован Н. Н. Боголюбовым для нек-рых задач статистич. механики, связанных с вычислением функций распределения s частиц (s = 1, 2, . N) для систем многих взаимодействующих частиц. Малым параметром в задачах статистич. механики может служить как малая константа взаимодействия, так и малая плотность частиц в системе. В одном из этих приближений можно выразить высшие s-частичные функции распределения через функции распределения одной частицы. При этом уже в первом приближении В. т. можно получить из системы кинетич. уравнений известные уравнения Больцмана, а также уравнения Ландау, Власова и Боголюбова-Ленарда-Балеску, широко применяемые в теории плазмы.

Следует отметить, что перечисленные методы развиты в применении к уравнениям с малым параметром, входящим в них регулярным образом (не при старшей производной). В то же время, напр., уравнение Ван дер Поля в форме Рэлея в случае больших ε автоматически сводится к уравнению, в к-ром малый параметр стоит перед старшей производной. Для задач такого типа, требующих особого подхода, развиты мощные методы исследования (см. [14], [15], [16], [17]).

Именно задачи с малым параметром при старшей производной типичны для проблем статистич. механики и гидродинамики. Примером может служить Навье-Стокса уравнение в предположении малых коэффициентов вязкости и теплопроводности, имеющее в качестве нулевого приближения уравнения идеальной жидкости Эйлера. Поиск наилучшего приближения в данной задаче усложнен указанным условием.

4) Большое значение методы В. т. имеют в области квантовой механики, где, такие как и в классической, точные решения получены лишь в задаче двух тел, формально сводимой к задаче одного тела во внешнем потенциальном поле. Здесь используются две формы В. т.: одна для стационарных состояний, другая для расчета вероятностей переходов из одного стационарного состояния в другое в схеме метода матрицы рассеяния. В. т. формулируется в квантовой механике как задача на собственные значения для линейного самосопряженного оператора вида:

где ε — малый параметр, причем известно решение задачи на собственные значения для «невозмущенного» оператора H₀, т. е. задана полная система собственных функций <ψ (0) _n> и собственных значений Е 0 _n и требуется найти спектр оператора Н.

В предположении малости ε волновые функции

и собственные значения энергии Е_n могут быть найдены в виде рядов

по степеням возмущения ε. Тогда для возмущения n-состояния В. т. дает следующий результат:

Здесь V_mn — матричный элемент оператора возмущения, определяемый согласно правилу (V̂ = εH₁):

где dq — элемент объема. Условие применимости В. т. к таким задачам:

нарушается в случае вырождения уровня энергии невозмущенной системы: вырожденному уровню энергии Е (0) _n отвечает s состояний <ψ (0) _nj>, j = 1, 2, . s (s — кратность вырождения). В этом случае применяется нек-рая модификация В. т.: вначале учитывают влияние возмущения на вырожденные состояния, а влияние других уровней рассматривается как малое возмущение; строятся линейные комбинации s функций вырожденного состояния, причем для коэффициентов С (0) _r построенной комбинации получены уравнения вида

Поправка к энергии Е (1) _n находится из секулярного уравнения системы (9). Решения <Е (1) _n,p>, p = 1, . s этого уравнения s-й степени представляют в (9) и находят <С (0) _r,p> и волновую функцию:

после снятия вырождения. Поправки следующего порядка находят методами обычной В. т.

В нестационарном случае задача В. т. ставится в терминах вероятностей перехода из состояния ψ (0) _n в состояние &#968 (0) _m. В. т. может применяться в гейзенберговском, шрёдингеровском представлениях или же в представлении взаимодействия.

В квантовой механике есть также принципиально другого типа задачи о нахождении так наз. рассеяния матрицы двух или нескольких частиц. В особенности такие задачи важны для квантовой электродинамики, где имеется малый параметр — постоянная тонкой структуры.

Проблема вычисления вероятностей перехода сводится к исследованию гамильтониана вида:

где Н₀ — свободный гамильтониан, а Н₁ — гамильтониан взаимодействия, к-рый по предположению включается в «отдаленном прошлом» (t = -∞) и выключается в «отдаленном будущем» (t = +∞).

В представлении взаимодействия Шрёдингера уравнение имеет вид:

Посредством замены переменных

можно получить для состояния φ уравнение

Связь между начальными состояниями φ_in, описывающими «входящие» частицы, и конечными состояниями φ_out описывающими «выходящие» частицы, формулируется в терминах так наз. оператора рассеяния S, определяемого соотношением вида:

Формально решение уравнения (10) можно построить методом последовательных приближений в виде разложения по степеням малости взаимодействия:

В квантовой теории поля справедлива аналогичная формула, в к-рую вместо H₁(t) входит соответствующая плотность лагранжиана, причем используется представление S-оператора через T-произведение:

Действие оператора хронологического упорядочения т определяется правилами:

причем это T-произведение формально не определено для совпадающих аргументов. Для преодоления такого рода трудностей, возникающих в методе В. т. в квантовой теории поля, созданы специальные методы регуляризации. Релятивистски инвариантная В. т. используется для вычисления так наз. S-матрицы, элементы к-рой определяют вероятности переходов между квантовыми состояниями различных полей под влиянием взаимодействия между ними.

Лит.: [1] Роinсаré Н., Les méthodes nouvelles de la mécanique céleste, P., t. 1-3, 1892-97; Пуанкаре A., Избр. труды, т. 1-3, M., 1971 — 74; [2] Шарлье К., Небесная механика, пер. с нем., М., 1966; [3] Биркгоф Дж. Д., Динамические системы, пер. с англ., М.-Л., 1941; [4] Колмогоров А. Н., О динамических системах с интегральным инвариантом на торе, «Докл. АН СССР», 1953, т. 93, № 5; [5] Арнольд В. И., Математические методы классической механики, М., 1974; [6] Мозер Ю., Лекции о гамильтоновых системах, пер. с англ., М., 1973; [7] Боголюбов Н. Н., Крылов Н. М., в кн.: Збiрник праць з нелiнiйноï механiки, К., 1937, с. 55-112; [8] их же, Введение в нелинейную механику, К., 1937; [9] Боголюбов Н. Н., Mитропольский Ю. А., Асимптотические методы в теории нелинейных колебаний, 5 изд., М., 1974; [10] Моисеев Н. Н., Асимптотические методы нелинейной механики, М., 1969; [11] Челомей В. Н., «Докл. АН СССР», 1956, т. 110, №3; [12] Боголюбов Н. Н., Митропольский Ю. А., Самойленко А. М., Метод ускоренной сходимости в нелинейной механике, К., 1969; [13] Боголюбов Н. Н., О некоторых статистических методах в математической физике, К., 1945; [14] Дородницын А. А. «Прикл. матем. и мех.», 1947, т. 11; [15] Тихонов А. Н., «Матем. сб.», 1948, т. 22, с. 193-204; [16] Понтрягин Л. С., «Изв. АН СССР. Сер. матем.», 1957, т. 21, с. 607; [17] Мищенко Е. Ф., «Изв. АН СССР. Сер. матем.», 1957, т. 21, с 607; «Изв. АН СССР. Сер. матем.», 1957, т. 21, с. 627; [18] Блохинцев Д. И., Основы квантовой механики, 5 изд., М., 1976; [19] Боголюбов Н. Н., Лекцiï з квантовоï статистики, К., 1949; [20] его же, Избранные труды, т. 2, К., 1970; [21] БоголюбовН. Н., Ширков Д. В., Введение в теорию квантованных полей, 3 изд., М., 1976; [22] Боголюбов Н. Н., Логунов А. А., Тодоров И. Т., Основы аксиоматического подхода в квантовой теории поля, М., 1969; [23] Ахиезер А. И., Берестецкий В. Б., Квантовая электродинамика, 3 изд., М., 1969; [24] Маслов В. П., Теория возмущений и асимптотические методы, М., 1965.

Н. Н. Боголюбов (мл.).

1. Математическая Энциклопедия. Т. 1 (А — Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] — М., «Советская Энциклопедия», 1977, 1152 стб. с илл.