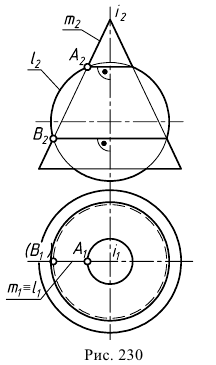
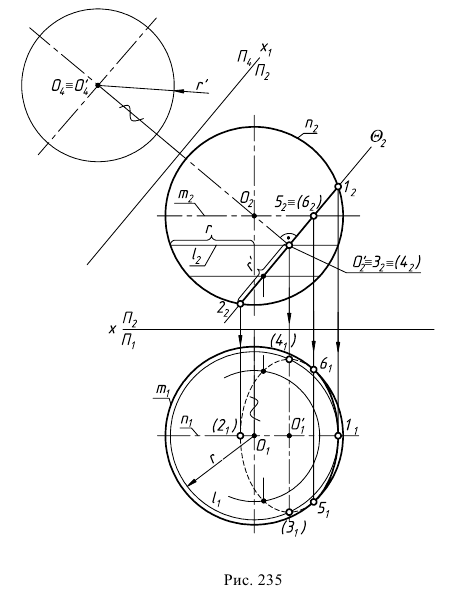
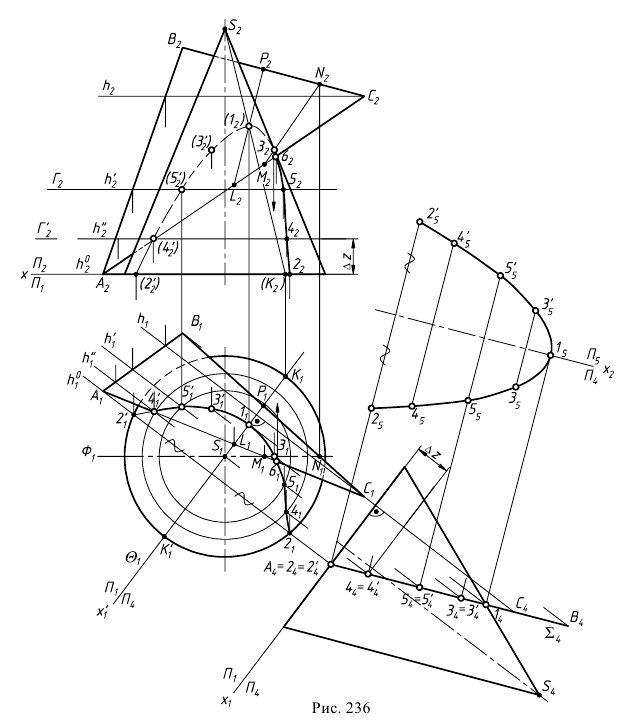
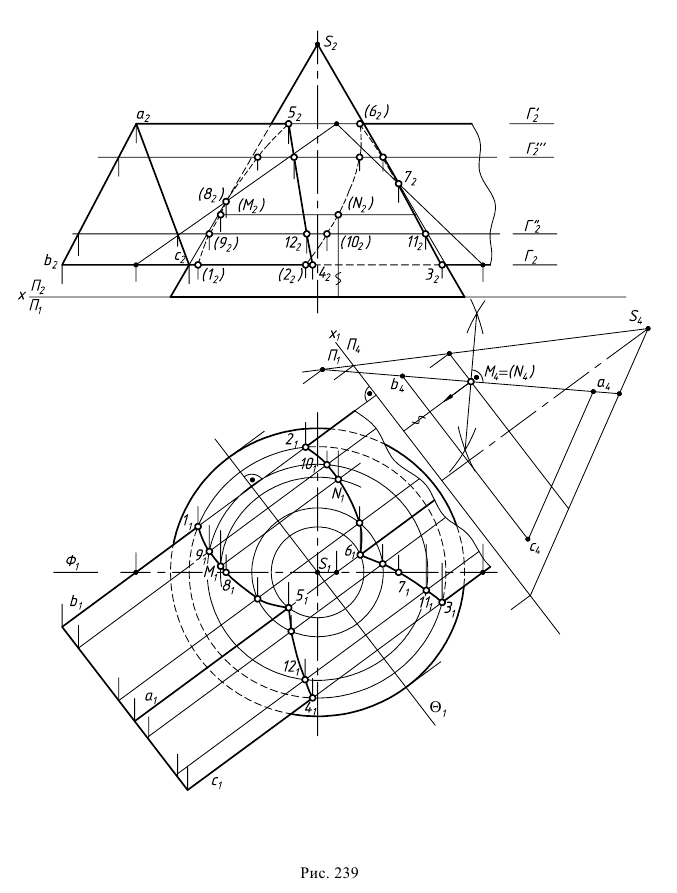
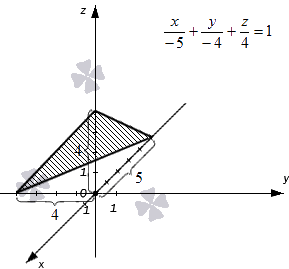
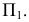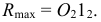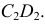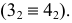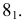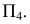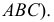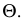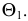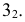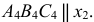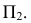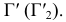Сфера заданная уравнением пересечена плоскостью
19.1. Определения шара, сферы и их элементов
С шаром и сферой мы уже знакомы. Напомним их определения.
Определение. Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не большем данного R ( R > 0). Данная точка называется центром шара, а данное расстояние R — радиусом шара .
Определение. Сферой называется множество всех точек пространства, находящихся от данной точки на расстоянии, равном данному R. Данные точка и расстояние R называются соответственно центром и радиусом сферы.
На рисунке 193 изображён шар с центром О и радиусом R = OА.
Из определений шара и сферы следует, что шар с центром О и радиусом R является объединением двух множеств точек: 1) множества точек M пространства, для которых OM (они называются внутренними точками шара и образуют его внутренность); 2) множества всех М, для которых ОМ = R (эти точки являются граничными точками шара, а их объединение составляет границу шара, которая называется шаровой поверхностью и является сферой c центром О и радиусом R ) .
Радиусом шара называют также всякий отрезок, соединяющий центр шара с точкой шаровой поверхности. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара . Концы любого диаметра шара называются диаметрально nротивоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара ( сферы ) . На рисунке 193 отрезки ОА, ОВ, ON, OS — радиусы шара; отрезки АВ , NS — диаметры шара; A и B — диаметрально противоположные точки шара. Из определения диаметра шара следует, что он равен удвоенному радиусу шара.
Покажем, что шар — тело вращения. Для этого рассмотрим полукруг F с центром О и радиусом R (рис. 194, а ). При вращении полукруга F вокруг прямой, содержащей его диаметр NS, образуется некоторое тело F 1 (рис. 194, б ). Так как вращение вокруг прямой — движение и точка О принадлежит оси l вращения, то каждая точка тела F 1 удалена от точки O на расстояние, не большее R (движение сохраняет расстояния между точками). Это означает, что тело F 1 есть шар с центром О и радиусом R. Кроме того, при вращении границы полукруга — полуокружности — вокруг прямой l образуется сфера. Прямая, содержащая любой диаметр шара, может быть рассмотрена как ось вращения. Следовательно, сечением шара плоскостью, перпендикулярной его оси вращения l и пересекающей шар, является круг, а сечением сферы такой плоскостью — окружность этого круга; центр круга (окружности) есть точка пересечения секущей плоскости с осью l.
Плоскость, проходящая через центр шара (сферы), называется диаметральной плоскостью шара ( сферы ) . Сечением шара диаметральной плоскостью является круг, радиус которого равен радиусу шара. Такой круг называется большим кругом, а его окружность — большой окружностью ; большая окружность является пересечением сферы и её диаметральной плоскости.
19.2. Изображение сферы
Рассмотрим сферу, диаметр NS которой проведён вертикально (рис. 195, а ). Большая окружность, по которой сферу пересекает диаметральная плоскость, перпендикулярная диаметру (оси) NS, называется экватором , а точки N и S — полюсами сферы . Окружность, ограничивающая круг — изображение сферы, — называется абрисом или очерковой линией .
Типичная ошибка (!) при изображении сферы (рис. 195, б ) в том, что, изображая её экватор эллипсом, полюсы изображают расположенными на абрисе.
Для верного и наглядного изображения сферы вспомним, как в курсе черчения изображают фигуру на комплексном двухкартинном чертеже (эпюре) посредством ортогонального её проектирования на две взаимно перпендикулярные плоскости, одну из которых называют фронтальной (обозначают V ) , а другую — профильной (обозначают W ) плоскостями проекций.
Сферу расположим так, чтобы её ось N ′ S ′ была параллельна профильной ( W ), но не параллельна фронтальной ( V ) плоскостям проекций. Тогда ортогональные проекции сферы на плоскости V и W имеют вид, изображённый на рисунке 196. На нём: равные круги — проекции сферы на плоскости V и W ; отрезки A 1 B 1 и N 1 S 1 — профильные проекции соответственно экватора и оси сферы; точки N, S — фронтальные проекции полюсов (строятся с помощью линий связи); точки А, В — фронтальные проекции концов диаметра экватора, параллельного фронтальной плоскости (строятся с помощью линий связи); отрезок CD — фронтальная проекция диаметра C ′ D ′ сферы, перпендикулярного профильной плоскости; эллипс с осями АВ и CD — фронтальная проекция экватора. При таком расположении относительно плоскостей проекций сфера изображается так, как показано на рисунках 195, a ; 196, a.
Обратите внимание! Полюсы N и S не лежат на абрисе, и экватор изображается эллипсом. При этом положение полюсов N и S и положение вершин А и В эллипса-экватора взаимосвязаны.
Действительно, из равенства △ ОBF = △ ЕNО (см. рис. 196, а ) следует: OВ = EN, BF = NO. Это означает: а) если изображены полюсы N и S сферы, то вершины А и В эллипса — изображения экватора определяются из равенств OВ = ОА = NE, где NE || OD ; б) если изображён экватор (т. е. дана малая ось AB эллипса-экватора), то положение полюсов N и S определяется из равенств ON = OS = BF, где BF || OD.
На рисунке 197, а — верное и наглядное изображение сферы, на рисунке 197, б — изображение сферы верное (почему?), но не наглядное; на рисунке 197, в — неверное изображение (почему?).
ЗАДАЧА (3.106). Найти в пространстве множество вершин всех прямых углов, опирающихся на данный отрезок АВ.
Решени е. Если ∠ АМВ = 90 ° , то точка М принадлежит окружности с диаметром АВ (рис. 198, a ).
Проведём произвольную плоскость α , содержащую отрезок АВ. В этой плоскости множество всех точек М, из которых отрезок AB виден под прямым углом, есть окружность, для которой отрезок AB — диаметр. Точки А и В этому множеству точек не принадлежат. (Почему?) Таким образом, искомое множество вершин прямых углов, опирающихся на отрезок AB , есть сфера с диаметром AB . Точки А и В этому множеству точек-вершин не принадлежат.
19.3. Уравнение сферы
Составим уравнение сферы с центром А ( a ; b ; с ) и радиусом R в декартовой прямоугольной системе координат Oxyz.
Пусть М ( x ; у ; z ) — любая точка этой сферы (рис. 199). Тогда MA = R или MA 2 = R 2 . Учитывая, что MA 2 = ( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 , получаем искомое уравнение cферы
( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 .
Если начало системы координат совпадает с центром A сферы, то a = b = c = 0 , а сфера в такой системе координат имеет уравнение
x 2 + y 2 + z 2 = R 2 .
Из полученных уравнений следует, что сфера — поверхность второго порядка.
Так как для любой точки М ( х ; у ; z ) шара с центром А ( a ; b ; с ) и радиусом R выполняется МА ⩽ R, то этот шар может быть задан неравенством
( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 ⩽ R 2 .
При этом для всех внутренних точек М шара выполняется условие МА 2 R 2 , т. е.
( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 R 2 ,
для точек М шаровой поверхности — условие
т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 ,
для точек М вне шара — условие
т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 > R 2 .
19.4. Пересечение шара и сферы с плоскостью
Рассмотрим подробнее вопрос о пересечении шара и сферы с плоскостью. Имеет место следующая теорема.
Теорема 30 (о пересечении шара и сферы с плоскостью ) . 1) Если расстояние от центра шара до данной плоскости меньше радиуса шара, то пересечением шара с плоскостью является круг. Центром этого круга является основание перпендикуляра, проведённого из центра шара на плоскость, или сам центр шара, если плоскость проходит через этот центр. Пересечением сферы с плоскостью является окружность указанного круга. Радиус r сечения в этом случае равен r = 
Доказательств о. Пусть точка О — центр шара, R — его радиус; α — данная плоскость, точка A — основание перпендикуляра, проведённого из центра O на плоскость α . Обозначим ρ ( О ; α ) = | ОА | = d — расстояние от центра шара до плоскости α .
Рассмотрим каждый из случаев взаимного расположения шара и данной плоскости α .
1) ρ ( O ; α ) = d R и плоскость α не проходит через центр О шара (рис. 200). Докажем, что пересечение шара и плоскости есть круг с центром А и радиусом r = 

Действительно, пусть М — произвольная точка шара, принадлежащая плоскости α (см. рис. 200). В прямоугольном треугольнике AOM по теореме Пифагора ОM 2 = ОА 2 + АМ 2 , откуда AM = 



Обратно, пусть М — произвольная точка плоскости α , принадлежащая кругу с центром А и радиусом r = 
Если неравенства, которые использовались в предыдущем доказательстве, заменить равенствами, то, рассуждая аналогично, можно доказать, что при d R пересечением сферы и плоскости является окружность с центром А и радиусом r = 
Если плоскость α проходит через центр O шара, то d = 0, значит, r = R, т. е. сечением шара такой плоскостью является большой круг, а сечением сферы — большая окружность (см. рис. 200).
2) ρ ( O ; α ) = d = OA = R (рис. 201).
Так как ОА = ρ ( O ; α ) = R, то точка А, являющаяся основанием перпендикуляра из центра О шара на плоскость α , принадлежит шаровой поверхности, ограничивающей данный шар.
Пусть M — произвольная точка плоскости α , отличная от точки A (см. рис. 201). Тогда длины наклонной ОМ и перпендикуляра OA, проведённых из точки О к плоскости α , удовлетворяют неравенству OM > ОА = R. Значит, точка М не принадлежит шару. Следовательно, плоскость α имеет только одну общую точку с шаром — точку А.
3) ρ ( О ; α ) = ОА = d > R (рис. 202). Для любой точки М плоскости α выполняется (почему?) ОМ ⩾ d > R. Это означает, что на плоскости α нет точек шара. Теорема доказана. ▼
ЗАДАЧА (3.161). Через середину радиуса шара проведена перпендикулярная к нему плоскость. Радиус шара равен R. Найти: а) площадь получившегося сечения; б) площади боковой и полной поверхностей конуса, основанием которого служит получившееся сечение шара, а вершиной — центр шара; в) площади боковой и полной поверхностей правильной треугольной пирамиды, вписанной в этот конус.
Решени е. а) Пусть точка O — центр шара, OD — его радиус, точка С — середина радиуса OD ; α — секущая плоскость, проходящая через точку С перпендикулярно OD.
Рассмотрим сечение шара диаметральной плоскостью, проходящей через его радиус OD. Этим сечением является большой круг с центром О и радиусом R (рис. 203); АВ — диаметр круга — сечения данного шара плоскостью α .
Так как АВ ⟂ OD и точка С — середина радиуса OD, то отрезок AB равен стороне правильного треугольника, вписанного в окружность радиуса R, значит, АВ = R 
АС = r = 

б) Найдём площадь поверхности конуса с вершиной О и радиусом основания r = 
Образующая ОЕ конуса (рис. 204) равна радиусу R данного шара. Поэтому площадь боковой поверхности этого конуса равна
π r • R = π • 

а площадь его полной поверхности — 



в) Найдём площадь поверхности правильной треугольной пирамиды OEFK, вписанной в конус, радиус основания которого СK = r = 
Так как △ ЕFK — правильный, вписанный в окружность радиуса r = 




Площадь боковой поверхности пирамиды равна 3 S △ EOF = 
ОН = 


Тогда 

Следовательно, площадь полной поверхности пирамиды равна





Ответ: a) 






19.5. Плоскость, касательная к сфере и шару
Из теоремы 30 следует, что плоскость может иметь со сферой (с шаром) только одну общую точку.
Определение. Плоскость, имеющая только одну общую точку со сферой (с шаром), называется касательной плоскостью к сфере (шару), а их единственная общая точка называется точкой касания (рис. 205).
Также говорят, что плоскость касается сферы (шара) .
Любая прямая, лежащая в касательной плоскости к сфере и проходящая через точку их касания, называется касательной прямой к сфере ; эта прямая имеет со сферой единственную общую точку — точку касания, и радиус сферы, проведённый в точку касания, перпендикулярен касательной прямой.

Справедливо и обратное: если прямая a касается окружности большого круга сферы в точке М , то эта прямая касается в точке М самой сферы.
Более того, так как прямая a, касающаяся сферы в точке М , имеет со сферой лишь одну общую точку — точку М , то эта прямая касается любой окружности, по которой пересекаются данная сфера и любая (не только диаметральная) плоскость, проходящая через прямую a. А поскольку радиус, проведённый в точку касания прямой и окружности, перпендикулярен касательной прямой, то центры всех этих окружностей — полученных сечений сферы — лежат в плоскости, проходящей через точку М перпендикулярно касательной прямой a. При этом, если точка О — центр данной сферы радиуса R , точка А — центр окружности радиуса r , по которой пересекает сферу одна (любая) из плоскостей, проходящих через касательную в точке М прямую к данной сфере, ϕ — величина угла между этой секущей плоскостью и проходящей через точку М диаметральной плоскостью данной сферы, то справедливо равенство r = R • cos ϕ ( △ ОАМ — прямоугольный, так как отрезок ОА перпендикулярен секущей плоскости (почему?)).
Для плоскости, касательной к сфере, справедливы теоремы, аналогичные теоремам о прямой, касательной к окружности на плоскости.
Теорема 31. Если плоскость касается сферы, то она перпендикулярна радиусу, проведённому в точку касания.
Доказательств о. Пусть дана сфера с центром O и радиусом R. Рассмотрим плоскость α , касающуюся данной сферы в точке M (см. рис. 205) и докажем, что ОM ⟂ α .
Предположим, что радиус ОM — не перпендикуляр, а наклонная к плоскости α . Значит, расстояние от центра сферы до плоскости α , равное длине перпендикуляра, проведённого из центра О на плоскость α , меньше радиуса. Тогда по теореме 30 плоскость α пересекает сферу по окружности. Но по условию теоремы плоскость α касается сферы и имеет с ней единственную общую точку M. Пришли к противоречию, которое и доказывает, что OM ⟂ α . Теорема доказана. ▼
Справедлива обратная теорема.
Теорема 32. Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведённому в эту точку, то она касается сферы.
Доказательств о. Пусть плоскость α проходит через точку M сферы и перпендикулярна радиусу ОM (см. рис. 205). Значит, расстояние от центра сферы до плоскости равно радиусу ОM. Тогда по теореме 30 плоскость α и сфера имеют единственную общую точку M, следовательно, плоскость α касается сферы (в точке M ). Теорема доказана. ▼
Так как сечение шара плоскостью есть круг, то можно доказать, что для шара выполняются следующие метрические соотношения:
— диаметр шара, делящий его хорду пополам, перпендикулярен этой хорде;
— отрезки всех касательных прямых, проведённых к шару из одной расположенной вне шара точки, равны между собой (они образуют поверхность конуса с вершиной в данной точке, а точки касания этих прямых — окружность основания этого конуса);
— произведение длин отрезков хорд шара, проходящих через одну и ту же внутреннюю точку шара, есть величина постоянная (равная R 2 – a 2 , где R — радиус шара, a — расстояние от центра шара до данной точки);
— если из одной и той же точки вне шара проведены к нему секущая и касательная, то произведение длины отрезка всей секущей на длину отрезка её внешней части равно квадрату длины отрезка касательной (и равно a 2 – R 2 , где R — радиус шара, a — расстояние от центра шара до данной точки).
19.6. Вписанные и описанные шары и сферы
Определение. Шар называется вписанным в цилиндр, если основания и каждая образующая цилиндра касаются шара (рис. 206).
Цилиндр в таком случае называется описанным около шара. В цилиндр можно вписать шар тогда и только тогда, когда он равносторонний.
Определение. Шар называется описанным около цилиндра, если основания цилиндра служат сечениями шара (рис. 207).
Цилиндр при этом называют вписанным в шар. Около любого цилиндра можно описать шар. Центром шара служит середина оси цилиндра, а радиус шара равен радиусу круга, описанного около осевого сечения цилиндра.
Определение. Шар называется описанным около конуса, если основание конуса — сечение шара, а вершина конуса принадлежит поверхности шара (рис. 208).
Конус при этом называют вписанным в шар.
Центр шара, описанного около конуса, совпадает с центром круга, описанного около осевого сечения конуса, а радиус шара равен радиусу этого круга.
Определение. Шар называется вписанным в конус, если основание и все образующие конуса касаются шара.
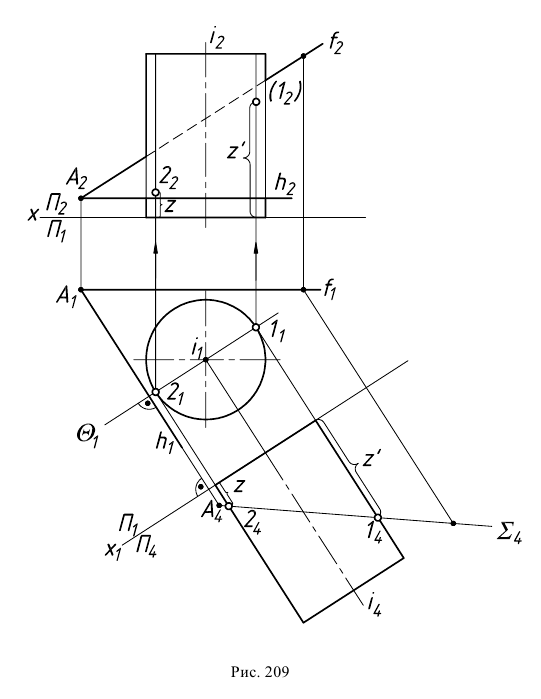
Конус при этом называют описанным около шара (рис. 209). Центр вписанного в конус шара совпадает с центром круга, вписанного в осевое сечение конуса, а радиус шара равен радиусу этого круга.
Определение. Шар называется вписанным в многогранник, если он касается всех граней многогранника.
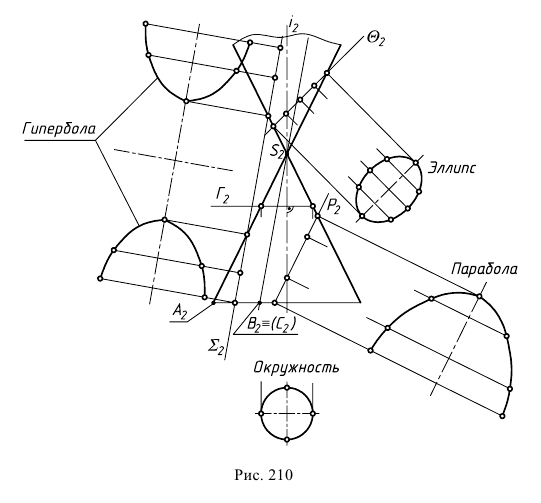
Многогранник в таком случае называют описанным около шара (рис. 210).
Не во всякий многогранник можно вписать шар. Например, вписать шар можно в любую треугольную или правильную пирамиду. А в прямую призму, в основании которой лежит прямоугольник, не являющийся квадратом, шар вписать нельзя.
При нахождении радиуса r вписанного в многогранник шара (если таковой существует) удобно пользоваться соотношением
V многогр = 
Шар называется вписанным в двугранный угол, если он касается его граней. Центр вписанного в двугранный угол шара лежит на биссекторной плоскости этого двугранного угла. При этом для радиуса r шара, вписанного в двугранный угол, величины α этого угла и расстояния m от центра шара до ребра двугранного угла справедлива формула: r = m • sin 
Шар называется вписанным в многогранный угол, если он касается всех граней многогранного угла. При решении задач, в которых рассматриваются вписанные в многогранный угол шары, удобно пользоваться соотношением: r = m • sin 
Если все плоские углы трёхгранного угла равны по 60 ° , то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно 3 r ; если все плоские углы трёхгранного угла прямые, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно r 
Определение. Шар называется описанным около многогранника, если все вершины многогранника принадлежат поверхности шара (рис. 211) . Многогранник при этом называют вписанным в шар.
Не около всякого многогранника можно описать шар. Например, около любой правильной или любой треугольной пирамиды шар описать можно, а около четырёхугольной пирамиды, в основании которой лежит ромб, не являющийся квадратом, шар описать нельзя (около ромба нельзя описать окружность). Более того, нельзя описать шар около любой наклонной призмы.
Вообще, для того чтобы около многогранника можно было описать шар, необходимо, чтобы около любой его грани можно было описать круг. При этом центр описанного шара может лежать как внутри многогранника, так и вне его или на его поверхности (даже на ребре многогранника), и проектируется в центр описанного около любой грани круга. Кроме того, перпендикуляр, опущенный из центра описанного около многогранника шара на ребро многогранника, делит это ребро (как хорду шара) пополам.
Мы уже говорили о пирамидах, все рёбра которых одинаково наклонены к основанию. Около таких пирамид всегда можно описать шар, центр которого лежит на луче, содержащем высоту пирамиды.
Высота h пирамиды, радиус R к описанного около основания пирамиды круга и радиус R описанного около этой пирамиды шара связаны соотношением:
( R – h ) 2 + 
Приведём формулы для вычисления радиусов вписанных и описанных шаров для правильных многогранников с ребром a.
В задачах иногда ещё рассматривают шары, касающиеся всех рёбер данного многогранника. Для куба, например, такой шар существует и его радиус равен 
19.7. Площади поверхностей шара и его частей
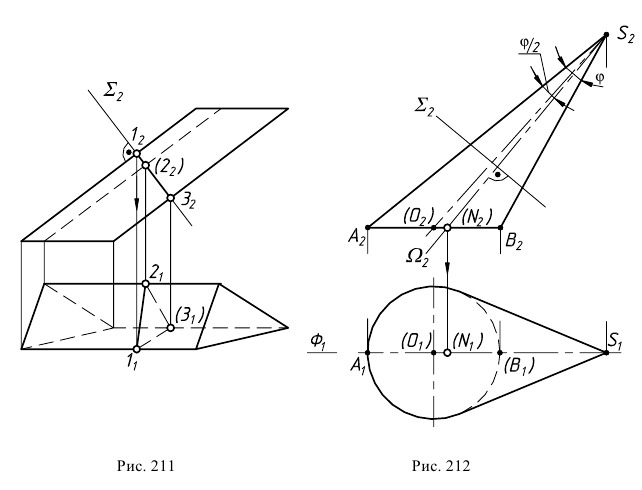
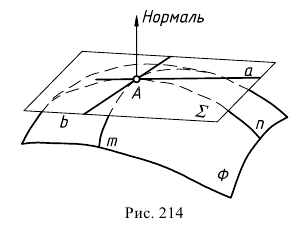
Часть шара, заключённая между секущей плоскостью и одной из двух частей его сферической поверхности, называется шаровым сегментом (рис. 212 и 214). Поверхность шарового сегмента называется сегментной поверхностью : она представляет собой часть шаровой поверхности, отсекаемую какой-нибудь плоскостью. Круг АВ, по которому плоскость пересекает шар, называется основанием шарового сегмента, а окружность этого круга — основанием сегментной поверхности. Отрезок ОС радиуса, перпендикулярного секущей плоскости, называется высотой шарового сегмента ( сегментной поверхности ) .
Часть шара, заключённая между двумя параллельными секущими плоскостями, называется шаровым слоем (см. рис. 212, 214). Поверхность шарового слоя называется шаровым поясом. Шаровой пояс — часть шаровой поверхности, заключённая между двумя параллельными секущими плоскостями. Перпендикуляр, проведённый из точки одного основания к плоскости другого, называется высотой шарового слоя ( шарового пояса ).
Сегментную поверхность и шаровой пояс можно рассматривать как поверхности вращения: в то время, как при вращении полуокружности CAA 1 D (см. рис. 212) вокруг диаметра CD образуется шаровая поверхность (сфера), при вращении дуги СА этой полуокружности вокруг того же диаметра образуется сегментная поверхность, а при вращении дуги AA 1 — шаровой пояс.
Тело, образованное при вращении кругового сектора с углом ϕ ( ϕ ° ) вокруг прямой, которая содержит диаметр круга, не имеющий с круговым сектором общих внутренних точек, называется шаровым сектором .
Из этого определения следует, что поверхность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса (рис. 213, а , б ) или из поверхности шарового пояса и боковых поверхностей двух конусов (рис. 213, в, г ).
На рисунке 214 изображены различные элементы шара и сферы (шаровой сектор имеет простейший вид).
Рассмотрим вопрос о вычислении площадей сферы, сегментной поверхности, шарового пояса и шарового сектора.
а) Площадь сферы. Пусть ABCDEF — правильная ломаная линия, вписанная в данную полуокружность; a — длина её апофемы (рис. 215). При вращении полуокружности вокруг её диаметра AF образуется сфера, а при вращении ломаной ABCDEF вокруг этого же диаметра AF образуется некоторая поверхность Ф .
За площадь сферы, образованной вращением полуокружности вокруг её диаметра, принимают предел, к которому стремится площадь поверхности Ф, образованной вращением вокруг того же диаметра правильной n- звенной ломаной линии, вписанной в полуокружность, при n → + ∞ ( число сторон неограниченно возрастает ).
Поверхность Ф является объединением поверхностей, образованных вращением звеньев ломаной линии, вписанной в полуокружность, вокруг её диаметра. Этими поверхностями являются боковые поверхности либо конуса (для первого и последнего звеньев ломаной), либо цилиндра (для звеньев, параллельных оси вращения; их может и не быть), либо усечённого конуса (для всех остальных звеньев ломаной).
При вычислении площадей получившихся поверхностей воспользуемся следствиями из теорем 26, 27, 29. Площадь S i ( i = 1, 2, . n ) поверхности, образованной вращением любого звена, равна произведению 2 π , расстояния b i от середины звена до центра сферы и длины m i проекции этого звена на ось вращения, т. е. S i вращ = 2 π • b i • m i .
Так как ломаная — правильная, то все b i равны апофеме a n данной n- звенной ломаной, а m 1 + m 2 + m 3 + . + m n = 2 R и S 1 + S 2 + S 3 + . + S n = 4 π • a n • R . Причём a n = 

Следовательно, предел площади поверхности Ф при n → ∞ равен 4 π R • R = 4 π R 2 . Этот предел и принимается за величину площади сферы радиуса R :
S сферы = 4 π R 2 .
б) Площади сегментной поверхности и шарового пояса. Если правильная ломаная вписана не в полуокружность, а в некоторую её часть, например в дугу AD (см. рис. 215), при вращении которой образуется сегментная поверхность, то рассуждения, аналогичные предыдущим, приводят к выводу:
S сегм. поверх = 2 π Rh ,
где h — высота сферического сегмента.
Если же ломаная вписана в дугу ВЕ (см. рис. 215), при вращении которой образуется шаровой пояс, то получим:
S шар. пояса = 2 π Rh ,
где h — высота шарового пояса.
Проделайте эти рассуждения самостоятельно.
в) Площадь поверхности шарового сектора. Эта площадь может быть получена как сумма площадей поверхности сферического сегмента и боковой поверхности одного конуса (см. рис. 213, а, б ) или как сумма площадей поверхности сферического слоя и боковых поверхностей двух конусов (см. рис. 213, в, г ).
Рассмотрим частный случай (см. рис. 213, а, б ). Если R — радиус сферы, h — высота шарового сегмента, то площадь боковой поверхности конуса с вершиной в центре сферы, образующей R , и радиусом основания 

S шар. сект = π R (2 h + 
ЗАДАЧА (3.418). Основанием треугольной пирамиды SABC является равносторонний треугольник АВС , сторона которого равна 4. Известно также, что AS = BS = 
Решени е. Решим эту задачу двумя методами.
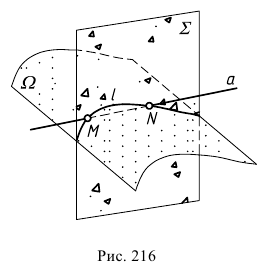
Первый метод ( геометрич е ски й). Пусть точка О — центр сферы, описанной около данной пирамиды; D — точка пересечения медиан правильного △ АВС ; точка Е — середина отрезка АВ (рис. 216).
Центр О сферы равноудалён от всех вершин △ АBС, поэтому принадлежит прямой, проходящей через точку D перпендикулярно плоскости АВС.
Так как точка Е — середина отрезка АВ, то SE ⟂ АВ ( AS = BS ) и СЕ ⟂ АВ ( △ АВС — правильный). Значит, по признаку перпендикулярности прямой и плоскости AB ⟂ ( CSE ) , поэтому ( CSE ) ⟂ ( ABC ) (по признаку перпендикулярности двух плоскостей). Это означает, что прямая OD, а следовательно, и точка О — центр сферы — лежат в плоскости CSE.
Точка D является центром окружности, описанной около △ АВС. (По этой окружности плоскость АВС пересекает сферу, описанную около данной пирамиды.) Если L — точка пересечения прямой СЕ и упомянутой окружности, то CL — её диаметр. Найдём длину диаметра CL.
В правильном △ AВС имеем: CE = 




Далее △ BSE ( ∠ BES = 90 ° ): SE 2 = SB 2 – BE 2 = 19 – 4 = 15 (по теореме Пифагора); △ SEC (по теореме косинусов):
cos C = 


△ SLC (по теореме косинусов):
SL 2 = SC 2 + CL 2 – 2 SC • CL • cos C = 

Плоскость CSL проходит через центр О сферы, следовательно, пересекает сферу по большой окружности, которая описана около △ CSL. Значит, радиус R этой окружности равен радиусу сферы, описанной около данной пирамиды. Найдём длину радиуса R.
В треугольнике CSL имеем 







Находим площадь Q сферы:
Q = 4 π R 2 = 4 π • 

Второй метод ( коо р динатны й). Введём в пространстве декартову прямоугольную систему координат так, чтобы её начало совпадало с вершиной А данной пирамиды, направление оси абсцисс — с направлением луча АС, ось аппликат была перпендикулярна плоскости основания АВС пирамиды (рис. 217).
В этой системе координат вершины основания пирамиды имеют координаты: А (0; 0; 0), B (2; 2 
Обозначив через х, у, z координаты вершины S пирамиды, найдём их из условий: AS = BS = 
AS 2 = x 2 + y 2 + z 2 = 19,
ВS 2 = ( x – 2) 2 + ( y – 2 
C S 2 = ( x – 4) 2 + y 2 + z 2 = 9.
Решая систему уравнений


находим: х = 


Таким образом, вершина S имеет следующие координаты:
S 
Пусть центр O сферы имеет координаты a, b, с, а её радиус равен R. Так как сфера описана около пирамиды SABC, то OA 2 = OB 2 = OC 2 = OS 2 = R 2 . Это соотношение в координатном виде равносильно системе уравнений





Вычитая из первого уравнения четвёртое, получаем a = 2, после чего, вычитая из первого уравнения второе, получаем b = 
После вычитания третьего уравнения системы из первого её уравнения получаем:

Подставив в это уравнение вместо a и b найденные их значения, получаем с = 



Q = 4 π R 2 = 
Ответ: 
19.8. Объёмы шара и его частей
Рассмотрим фигуру, образованную вращением равнобедренного прямоугольного треугольника с гипотенузой 2 R вокруг прямой, проходящей через вершину прямого угла параллельно гипотенузе (рис. 218, а ). Объём этой фигуры равен разности объёма цилиндра с высотой 2 R , радиусом основания R и удвоенного объёма конуса высоты R , радиуса основания R :
V = π • R 2 • 2 R – 2 • 

Шар радиуса R (рис. 218, б ) и образованную выше фигуру вращения расположим между двумя параллельными плоскостями, расстояние между которыми равно 2 R . Шар при этом будет касаться каждой из данных плоскостей, а фигуру вращения расположим так, чтобы её ось вращения была перпендикулярна этим плоскостям (см. рис. 218). (Плоскость, которая содержит верхнее основание цилиндра и касается сферы в точке N , на рисунке не изображена.)
Будем пересекать наши фигуры плоскостями, параллельными данным плоскостям и удалёнными от центра шара на расстояние x (0 ⩽ x ⩽ R ).
При х = 0 площади сечений обеих фигур равны π • R 2 ; при х = R площади сечений равны нулю. В остальных случаях площадь сечения шара равна π • ( 
V шара = 
гдe R — радиус шара.
Для получения объёма шарового сегмента высоты h рассмотрим предыдущую ситуацию для R – h ⩽ x ⩽ R (при h R ) (рис. 218, 219). Применяя принцип Кавальери, получим: объём шарового сегмента равен разности объёма цилиндра высоты h и радиуса основания R и объёма усечённого конуса высоты h и радиусов оснований R и R – h , т. е.
V = π • h • R 2 – 
= 
При h > R объём шарового сегмента можно найти как разность объёма шара и объёма шарового сегмента высоты 2 R – h (рис. 220): V = 




Мы показали, что в шаре радиуса R объём любого шарового сегмента высоты h может быть вычислен по формуле:
V шар. сегм = 
или в другом виде
V шар. сегм = π • h 2 • 
Пересечение поверхности плоскостью и прямой с примерами
Содержание:
Задачи на нахождение общих точек у прямой и поверхности, построение линии пересечения плоскости с поверхностью, двух поверхностей определяют взаимное положение геометрических образов и относятся к классу позиционных.
Пересечение поверхности плоскостью
Линия пересечения поверхности с плоскостью представляет собой, в общем случае, плоскую кривую или ломаную линию, все точки которой одновременно принадлежат поверхности и секущей плоскости.
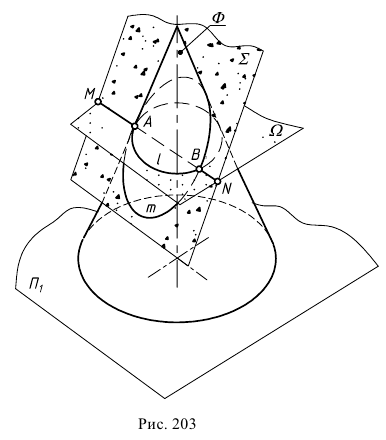
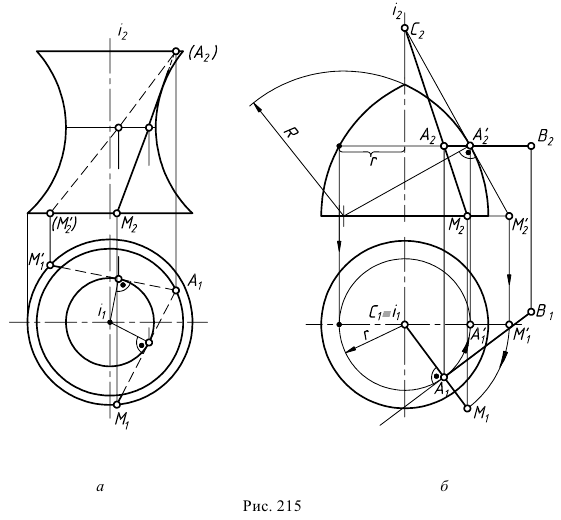
Аналитически для определения уравнения линии пересечения плоскости с поверхностью необходимо решить следующую систему уравнений:
где
Для графического построения точек линии пересечения поверхности с плоскостью используется общий способ нахождения точек, принадлежащих двум геометрическим образам — способ вспомогательных секущих поверхностей. В качестве секущих поверхностей используют вспомогательные плоскости.
На рис. 203 показана поверхность 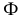
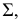
- заданные геометрические образы рассекают вспомогательной секущей плоскостью
которую выбирают так, чтобы она пересекла поверхность по графически простым линиям (прямым или окружностям);
- находят линии
и
пересечения вспомогательной секущей плоскости
с поверхностью
и плоскостью
соответственно;
- определяют точки
и
взаимного пересечения линий
и
лежащих в секущей плоскости
Точки
и
принадлежат обоим геометрическим образам, т.е. искомой линии пересечения
- последовательно выбирают ряд секущих плоскостей, построения при этом остаются теми же;
- полученные точки искомой линии пересечения соединяют с учетом видимости.
До начала построений необходимо сделать анализ взаимного расположения геометрических образов и искомой линии их пересечения, рационально выбрать вспомогательные секущие плоскости.
При анализе искомой линии пересечения и данных геометрических образов пользуются следующими основными положениями:
- Плоскость, пересекающая поверхность, может занимать как общее, так и частное положение относительно плоскостей проекций.
- Линия пересечения криволинейной поверхности с секущей плоскостью в общем случае — кривая линия.
- При пересечении сферы любой плоскостью в сечении всегда получается окружность.
- Сечение поверхности вращения плоскостью всегда будет фигурой симметричной, ось симметрии которой располагается в общей плоскости симметрии двух пересекающихся геометрических образов. Плоскостью симметрии секущей плоскости является любая плоскость, перпендикулярная ей. Плоскость симметрии поверхности вращения всегда проходит через ее ось. Таким образом, общая плоскость симметрии должна удовлетворять обоим условиям — проходить через ось вращения поверхности и быть перпендикулярной секущей плоскости.
- При пересечении линейчатой поверхности плоскостью точки искомой кривой находятся как точки пересечения образующих поверхности с данной секущей плоскостью.
- Линия пересечения многогранной поверхности с секущей плоскостью в общем случае — ломаная линия, вершинами которой служат точки пересечения ребер многогранной поверхности с секущей плоскостью, а сторонами — отрезки прямых пересечения граней поверхности с той же плоскостью.
- При пересечении прямого кругового конуса получается семейство различных кривых второго порядка (конические сечения) или прямые линии (образующие).
- При пересечении прямого кругового цилиндра могут получаться окружности, образующие или эллипсы.
- У цилиндрических, конических и призматических поверхностей выделяются так называемые нормальные сечения. Нормальным называется сечение цилиндра или призмы, перпендикулярное образующим. Нормальное сечение конуса — это сечение, перпендикулярное его оси симметрии.
- При пересечении поверхности открытого тора (кругового кольца) (рис. 204, а) с плоскостью получаются алгебраические кривые четвертого порядка. Их общее название — кривые Персея. На рис. 204 показаны сечения поверхности открытого тора различными плоскостями, которые расположены на расстоянии
от оси тора.
В зависимости от величин 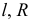
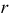
- — две окружности (см. рис. 204, б)
- — овалы с одной осью симметрии (см. рис. 204, в);
- — двухлепестковую кривую с узловой точкой в начале координат (см. рис. 204, г);
- — волнообразную кривую (см. рис. 204, д);
- — овал с двумя осями симметрии (см. рис. 204, е).
Построение искомой линии пересечения следует начинать с опорных точек кривой. Опорными точками кривой называют такие, которые выделяются особым расположением по отношению к плоскостям проекций или занимают особое место на кривой.
Опорными точками являются:
- — экстремальные точки линии пересечения, позволяющие судить, в каких пределах следует строить линию пересечения. К экстремальным относятся самая дальняя и самая ближняя точки, самая левая и самая правая, наивысшая и наинизшая точки линии пересечения, которые всегда располагаются в общей плоскости симметрии двух пересекающихся геометрических образов;
- — точки линии пересечения, лежащие на очерках поверхности и называемые точками изменения видимости. Проекции этих точек делят проекцию линии пересечения на видимую и невидимую части. Видимость линии пересечения определяется по видимости поверхности, на которой она лежит. Видима всегда та часть поверхности, которая ближе к наблюдателю;
- — характерные точки закономерных кривых — это вершины гиперболы или параболы, большая и малая оси эллипса.
Остальные точки линии пересечения называются промежуточными. Следует помнить, что приведенная классификация опорных точек условна. Экстремальные и характерные точки одновременно могут являться и точками изменения видимости. Характерные точки могут определять экстремальные положения линии пересечения.
Приведенный выше анализ задачи на пересечение поверхности с плоскостью дает наиболее общие закономерности, используемые при решении. Особенно следует выделить задачи построения нормальных сечений, сечений прямых круговых конуса и цилиндра, сечений линейчатых и нелинейчатых поверхностей, сечений плоскостями общего и частного положения.
Сечение поверхности проецирующей плоскостью
В случае, когда секущая плоскость является проецирующей, построение линии пересечения ее с поверхностью значительно упрощается.
Из рис. 203 видно, что линию 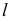
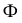
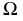
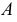
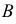
На рис. 205, а горизонтально проецирующая плоскость 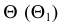
На рис. 205, б приведена схема нахождения точек линии пересечения поверхности вращения с фронтально-проецирующей плоскостью 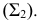
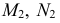
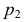
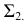
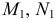
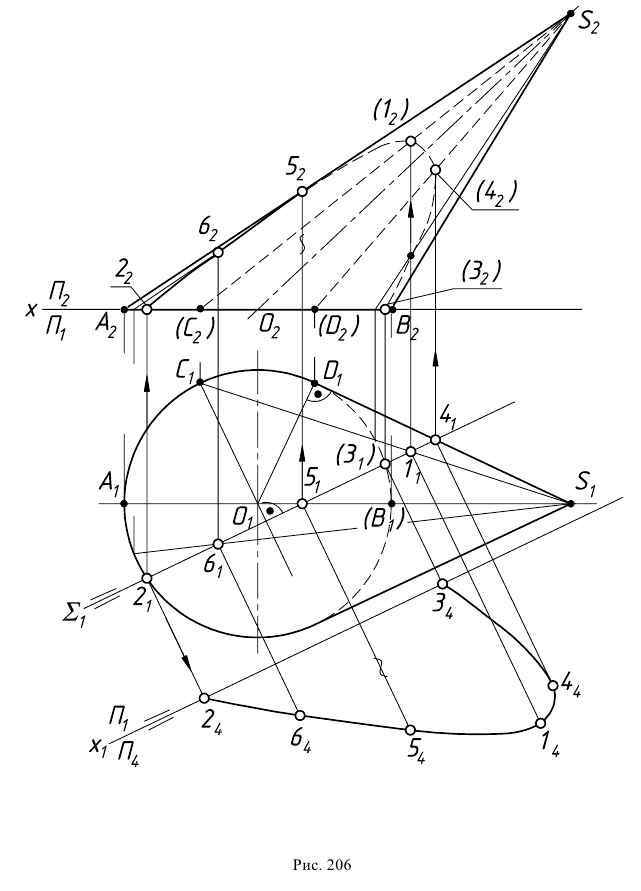
Построение сечения наклонного эллиптического конуса с круговым основанием горизонтально-проецирующей плоскостью 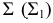
Горизонтальная проекция сечения совпадает с горизонтальным следом плоскости 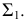
Наивысшая точка искомой кривой находится в общей плоскости симметрии двух пересекающихся г.о. Эта плоскость общего положения проходит через центровую линию 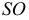
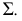
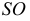
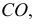
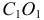
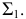
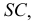
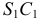
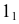
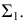
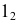
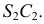
Самые низкие точки кривой располагаются на основании конуса. На горизонтальной проекции отмечаются точки 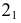
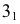
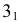
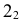
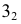
Горизонтальная проекция крайней правой точки 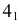
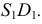
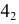
Точки изменения видимости располагаются на образующих, дающих фронтальный очерк поверхности, это образующие 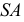
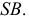
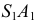
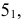
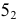
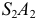
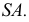
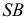
Для получения плавной кривой необходимо построить ряд промежуточных точек, таких как точка 6. Натуральная величина сечения находится проецированием на дополнительную плоскость проекций
Сечение поверхности плоскостью общего положения
В случае, когда секущая плоскость занимает общее положение, схема построения точек линии пересечения совпадает с приведенным выше алгоритмом решения задачи, проиллюстрированным на рис. 203.
В соответствии с этим алгоритмом на рис. 207 показано нахождение точек линии пересечения поверхности вращения с плоскостью общего положения 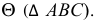
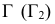
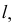
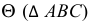
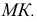
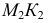
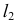
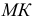
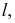
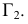
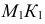
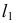
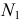
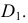
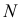
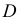
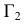
Полное решение задачи на пересечение поверхности конуса с плоскостью общего положения приведено ниже (рис. 236).
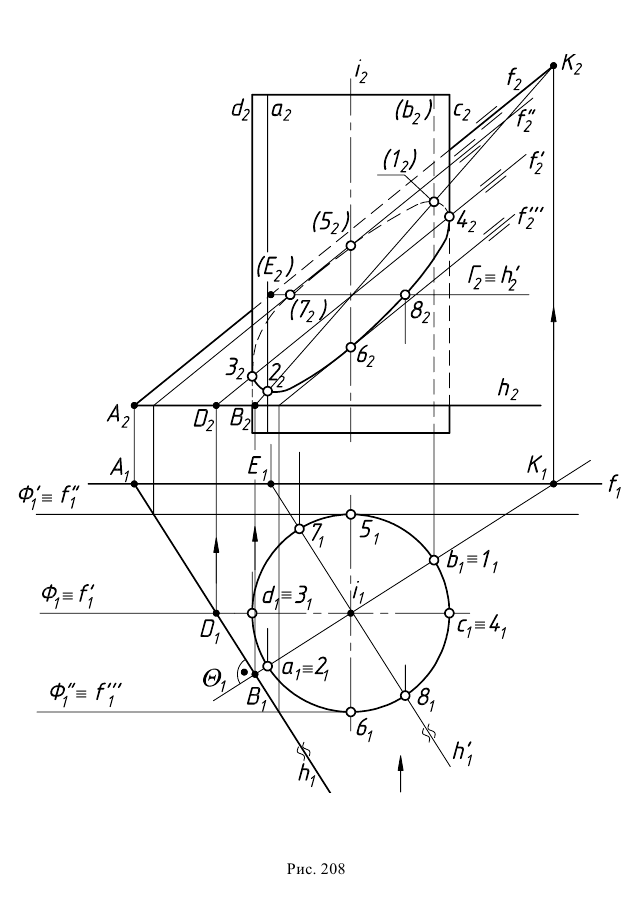
Рассмотрим применение способа вспомогательных секущих плоскостей для построения линии сечения цилиндра плоскостью. На рис. 208 заданы прямой круговой цилиндр и плоскость 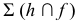
Плоскость 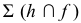
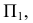
Построение линии пересечения начинают с опорных точек.
Высшая и низшая точки искомой кривой располагаются в общей плоскости симметрии пересекающихся геометрических образов. Такой плоскостью является горизонтально-проецирующая плоскость 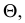
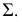
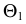
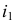
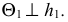
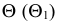
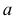
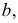
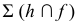
Горизонтальные проекции 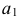
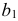
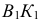
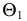
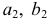
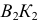
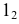
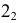
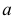
Точки изменения видимости линии пересечения всегда располагаются на очерке поверхности. Фронтальный очерк цилиндра определяют образующие 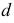
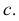
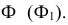
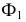
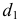
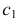
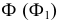
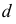
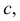
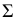
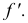
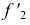
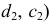
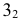
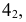
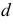
Точки изменения видимости 3 и 4 одновременно являются самой левой и самой правой точками искомой линии пересечения.
Для определения самой дальней 5 и самой ближней 6 точек эллипса проводятся вспомогательные секущие плоскости уровня 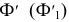
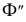
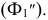
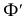
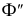
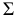
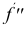
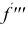
Для получения плавной кривой строятся промежуточные точки при помощи горизонтальных плоскостей уровня, которые рассекают цилиндр по окружностям, а данную плоскость по горизонталям. На рис. 208 построены промежуточные точки эллипса 7 и 8, лежащие в секущей плоскости 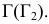
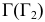
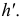
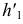
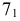
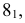
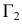
Полученные точки эллипса соединяют плавной кривой с учетом видимости. На фронтальной плоскости проекций видимой будет линия на передней половине цилиндра до образующих 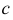
Ранее было показано, что построение линии пересечения поверхности с проецирующей плоскостью значительно проще, чем с плоскостью общего положения. Используя методы преобразования эпюра, можно секущую плоскость общего положения преобразовать в проецирующую и построить линию пересечения поверхности с плоскостью частного положения.
Пример такого преобразования приведен на рис. 209. Условие задачи соответствует задаче пересечения цилиндра с плоскостью общего положения (см. рис. 208).
Секущая плоскость общего положения в новой системе плоскостей проекций преобразована так, что она стала проецирующей. На новой плоскости проекций 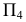
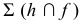
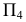
Если известна проекция линии пересечения на плоскости 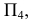
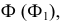
Конические сечения
Из многообразия конических поверхностей выделяют поверхность прямого кругового конуса, так как она обладает особыми свойствами. Коническая поверхность, кроме прямых линий (образующих), несет на себе семейства различных кривых второго порядка: эллипсов, окружностей, парабол и гипербол. Эти кривые получаются как конические сечения, то есть являются линиями пересечения поверхности конуса с плоскостями.
На рис. 210 показаны сечения прямого кругового конуса. В том случае, когда плоскость 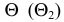
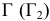
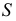
Если секущая плоскость 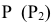
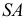
В том случае, когда секущая плоскость 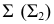
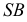
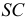
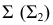
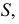
Построение линии пересечения прямого кругового конуса с плоскостью частного положения аналогично рассмотренным ранее задачам. Полное решение такой задачи с нахождением натуральной фигуры сечения приведено ниже (рис. 236).
В случае, когда рассматривается пересечение конической поверхности второго порядка и секущей плоскости общего положения, также можно определить вид линии пересечения. Для этого через вершину конической поверхности проводится плоскость, параллельная заданной, и определяется вид вырожденного сечения (примеры построения не приводятся).
Нормальные сечения
Нормальным называется сечение цилиндра или призмы плоскостью, перпендикулярной образующим. Нормальное сечение конуса — это сечение, перпендикулярное его оси симметрии. Любой конус или цилиндр называется всегда по нормальному сечению. Если нормальное сечение — окружность, то конус или цилиндр называются круговыми. Если нормальным сечением является эллипс, то поверхность называется эллиптической.
Пример построения нормального сечения призмы приведен на рис. 211. Ребра трехгранной призмы являются фронталями, поэтому плоскость, им перпендикулярная, будет фронтально-проецирующей 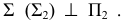
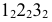
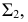
Для конической поверхности (рис. 212) при построении нормального сечения необходимо определить ось конуса, как линию пересечения двух плоскостей симметрии 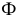
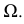
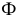
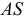
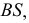
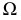
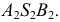
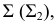
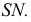
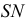
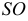
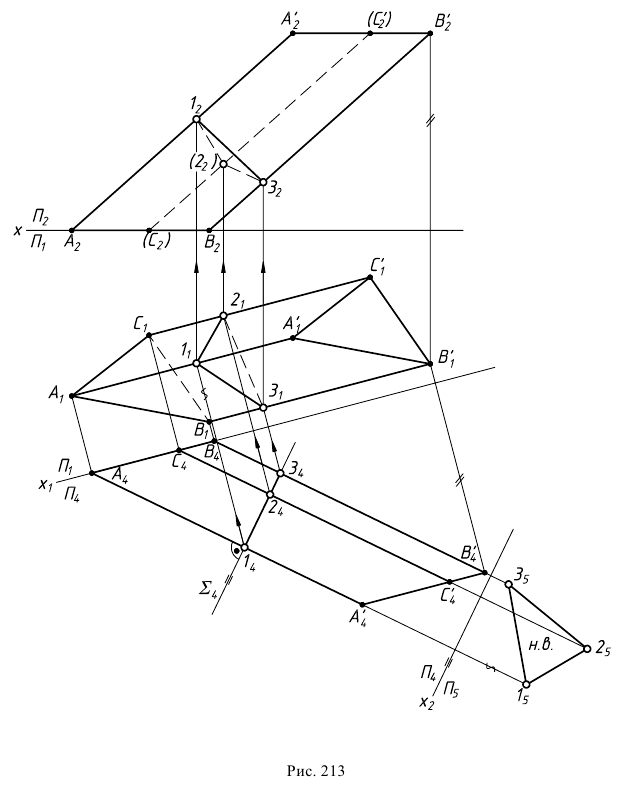
На рис. 213 показано построение нормального сечения призмы, у которой ребра занимают общее положение. Плоскость, перпендикулярная прямой общего положения, должна быть также общего положения относительно плоскостей проекций. Такую плоскость можно было бы задать горизонталью и фронталью, перпендикулярным ребрам призмы, а затем три раза решать задачу на пересечение прямой с плоскостью общего положения.
Однако в данном случае приведено решение, которое проецированием на дополнительную плоскость проекций сведено к частному, показанному на рис. 211. Новая плоскость проекций 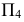
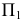
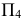
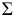
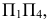
Нормальное сечение 
Плоскость, касательная к поверхности
Положение плоскости 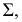
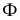
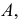
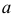
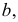
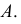
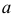
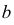
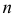
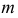
Плоскость может касаться поверхности либо в точке, либо по линии (прямой или плоской кривой). Касаясь поверхности в данной точке, плоскость может пересекать поверхность по одной или двум линиям. На поверхности могут быть точки, в которых нельзя провести касательную плоскость. Такие точки называются особыми. К их числу относятся точки самопересечения поверхности, точки ребра возврата, заостренные вершины поверхностей вращения (когда образующая пересекает ось вращения не под прямым углом).
Точки, в которых можно провести единственную касательную плоскость, называют обыкновенными.
Плоскость, касательная к линейчатой поверхности в произвольной точке на данной образующей, проходит через эту образующую. Сказанное объясняется тем, что каждая образующая является своей собственной касательной.
Задача построения касательной плоскости в точке 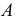
Однополосный гиперболоид вращения — поверхность дважды линейчатая. Через каждую точку этой поверхности можно провести две прямолинейные образующие. Они и определят искомую плоскость.
Касаясь поверхности в данной точке, эта плоскость пересекает гиперболоид по двум прямым. Горизонтальные проекции прямолинейных образующих построены как касательные к горловой окружности, проведенные из 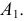
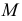
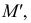
При построении касательной плоскости к нелинейчатой поверхности необходимо через заданную точку провести на поверхности две кривые. Касательные к ним определят искомую плоскость.
На рис. 215, б построена касательная плоскость к поверхности вращения в данной на ней точке
В качестве кривых, проходящих по поверхности через точку 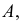
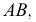
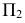
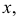
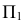
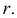
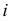
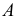
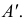
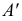
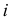
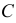
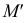
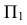
Теперь остается перевести меридиан и построенную касательную в первоначальное положение. Соединяя точку 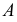
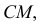
Пересечение прямой линии с поверхностью
Аналитически для определения координат точек пересечения прямой линии с поверхностью необходимо решить следующую систему уравнений:
где 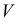
Графическое решение задачи на определение точек пересечения прямой линии с поверхностью аналогично задаче нахождения точки пересечения прямой линии с плоскостью. Точки пересечения прямой линии с поверхностью определяются способом вспомогательных секущих плоскостей. Алгоритм решения задачи следующий:
- через прямую
проводится вспомогательная плоскость
(рис.216);
- находится линия пересечения
вспомогательной плоскости
с данной поверхностью
- на пересечении полученной линии пересечения
с заданной прямой а найдутся искомые точки
и
- определяется видимость прямой.
Через прямую можно провести сколько угодно различных плоскостей, однако для упрощения решения задачи надо выбирать такую вспомогательную плоскость, в пересечении которой с данной поверхностью получились бы простые линии (прямые или окружности). Вспомогательная плоскость 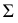
На рис. 217, а задана горизонтально-проецирующая прямая 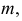
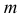
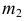
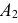
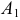
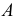
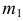
На рис. 217, б решена задача на пересечение горизонтали 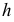
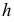
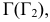
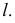
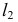
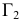
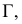
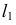
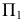
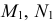
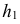
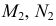
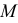
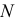
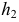
На горизонтальной плоскости проекции точки 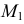
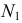
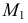
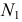
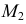
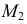
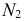
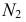
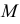
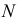
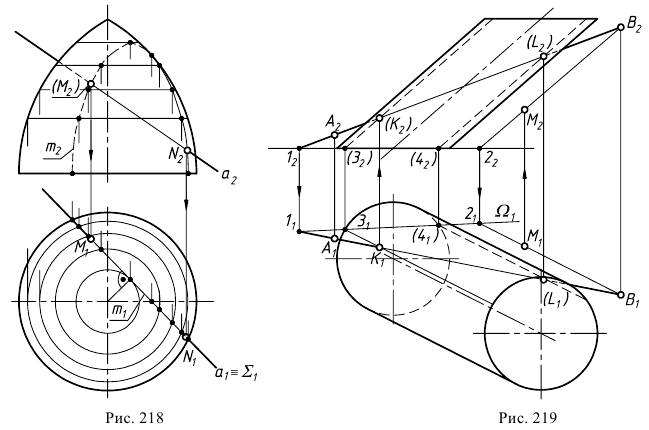
На рис. 218 приведена задача на построение точек пересечения прямой с поверхностью вращения. В качестве вспомогательной секущей плоскости выбрана горизонтально-проецирующая плоскость 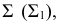
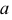
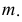
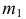
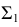
Для построения фронтальной проекции 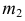
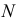
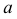
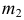
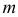
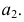
На горизонтальной плоскости проекций точки 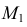
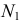
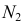
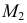
Во всех приведенных выше задачах вспомогательная секущая плоскость занимает частное положение. Вспомогательную плоскость общего положения удобно использовать в задачах при пересечении прямой линии с конической или цилиндрической поверхностью. При пересечении цилиндрической поверхности прямой линией вспомогательную плоскость проводят через данную прямую параллельно образующим цилиндра. В этом случае в сечении плоскости с цилиндром получаются прямые линии.
Пример решения задачи на пересечение прямой с цилиндром приведен на рис. 219. Задан наклонный цилиндр с круговыми основаниями. Для построения точек пересечения поверхности цилиндра с прямой линией 
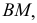
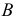
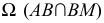
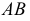
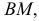
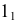
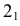
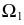
Горизонтальный след 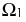
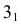
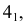
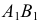
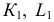
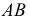
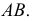
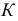
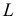
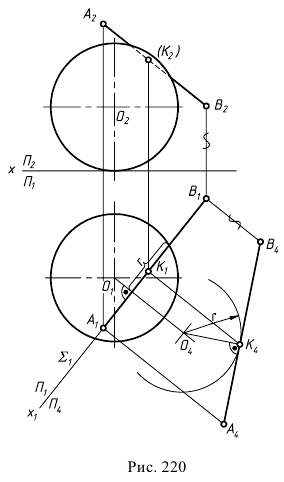
При решении задачи на пересечение поверхности прямой линией может оказаться, что данная прямая не пересекает, а лишь касается данной поверхности. В этом случае прямая является касательной к данной поверхности (рис. 220). На этом рисунке через горизонтальную проекцию 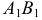
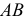
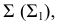
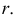
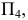
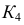
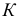
Пересечение поверхностей
Геометрическое место точек, принадлежащее одновременно двум поверхностям, называют линией пересечения (или линией перехода) данных поверхностей.
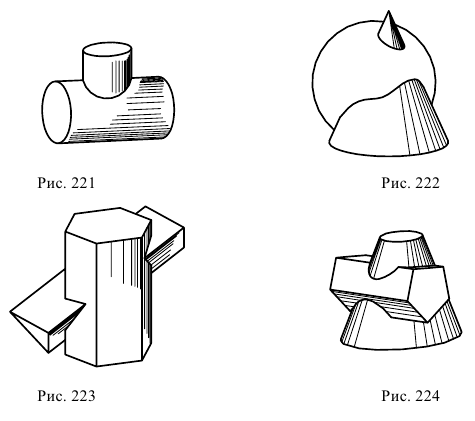
Линия пересечения двух поверхностей в общем случае представляет собой пространственную кривую. При частичном пересечении поверхностей (одна из поверхностей как бы «врезается» в другую) будет одна замкнутая линия пересечения (рис. 221). При полном пересечении поверхностей (одна из поверхностей пересекает другую насквозь) получаются две замкнутые линии пересечения (рис. 222). В случае двух многогранных поверхностей линия их пересечения является ломаной линией (рис. 223). Если одна из поверхностей кривая, а другая — гранная, то линия их пересечения состоит из участков представляющих собой плоские кривые линии, принадлежащие граням (рис. 224).
Обычно линию пересечения двух поверхностей строят по ее отдельным точкам, которые аналитически определяются при решении системы уравнений
В начертательной геометрии задачи на пересечение двух поверхностей решают путем введения вспомогательных секущих поверхностей-посредников. В качестве поверхностей-посредников применяют плоскости или сферы, поэтому различают способ вспомогательных секущих плоскостей и способ вспомогательных секущих сфер. Последний имеет разновидности: способ концентрических сфер и способ эксцентрических сфер. Применение того или иного способа зависит от типа данных поверхностей, их взаимного расположения, и расположения относительно плоскостей проекций.
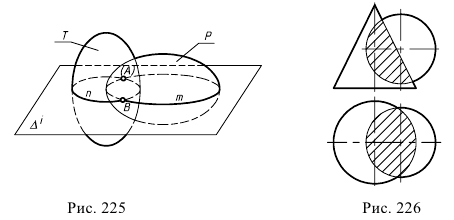
Построение общих точек, принадлежащих линии перехода поверхностей, поясняется на рис. 225 и осуществляется по общему для всех способов решения алгоритму:
- выбирают секущие поверхности-посредники
относительно данных поверхностей
такими, чтобы в пересечении получались графически простые линии (прямые, окружности), и проекции этих линий легко строились на эпюре;
- строят линии
и
по которым посредник пересечет обе поверхности;
- находят общие точки
и
пересечения линий
и
Эти точки принадлежат одному посреднику и одновременно двум данным поверхностям;
- применив последовательно несколько раз посредники и выявив ряд общих точек, соединяют их линией (последняя на рис. 225 не показана).
Каким бы способом не производилось построение линии пересечения поверхностей, при нахождении точек этой линии необходимо соблюдать определенную последовательность. У линии пересечения двух поверхностей так же, как и у линии пересечения поверхности с плоскостью (см. раздел VII. 1), различают опорные и промежуточные точки.
В первую очередь определяют экстремальные точки, так как они всегда позволяют видеть, в каких пределах расположены проекции линии пересечения, и где между ними имеет смысл строить промежуточные точки.
Далее определяют точки изменения видимости, которые отделяют видимую часть линии пересечения от невидимой. Эти точки всегда находятся на очерке той поверхности, которая расположена ближе к наблюдателю.
Строят точки на очерке другой поверхности. В точках, расположенных на очерках, проекции линии пересечения касаются очерковых линий пересекающихся поверхностей.
Для более точного построения линии пересечения данных поверхностей определяют промежуточные точки.
Следует иметь в виду, что проекции линии пересечения всегда располагаются в пределах заштрихованного контура наложения проекций двух пересекающихся поверхностей (рис. 226).
В случае, если одна из поверхностей является проецирующей, то строят проекцию линии пересечения только на одной плоскости проекций, к которой поверхность не перпендикулярна. На другой же плоскости проекция искомой линии совпадает с вырожденной проекцией поверхности (см. пример на рис. 240).
Способ вспомогательных секущих плоскостей
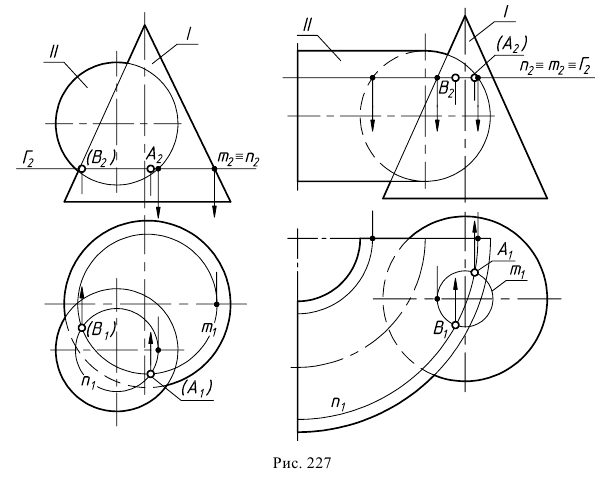
Способ вспомогательных секущих плоскостей частного положения (способ плоскостей общего положения в данном разделе не рассматривается) следует применять тогда, когда обе поверхности возможно пересечь по графически простым линиям некоторой совокупностью плоскостей уровня. Такие плоскости используют для нахождения промежуточных точек (рис. 227) после того, как найдены экстремальные точки.
Экстремальные точки располагаются в общей для двух поверхностей плоскости симметрии, которая проходит через оси этих поверхностей. Общая плоскость симметрии задана горизонтальным следом 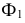
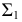
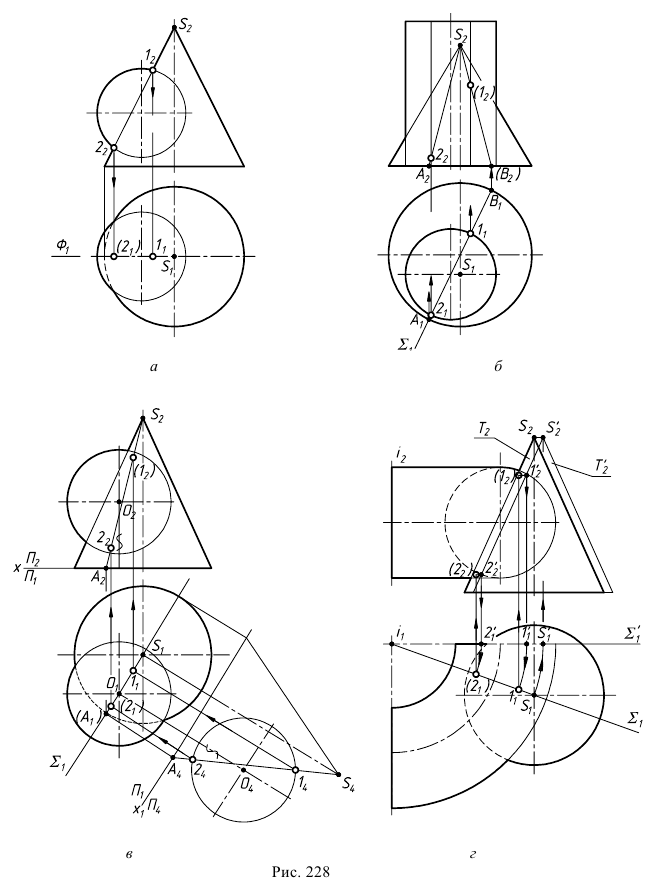
Если общая плоскость симметрии является плоскостью уровня (см. рис. 228, а), то фронтальные проекции высшей — 1 и низшей — 2 точек будут находиться на пересечении фронтальных очерков поверхности. Если общая плоскость симметрии не является плоскостью уровня, то возможны два варианта построения этих точек — без применения (см. рис. 228, б) и с применением (см. рис. 228, в, г) преобразования чертежа.
Так, на рис. 228, в сначала строят очерки поверхностей на дополнительную плоскость проекций 
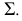
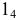
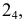
Для нахождения экстремальных точек можно воспользоваться также способом вращения вокруг проецирующей прямой. За ось вращения принимают ось одной из поверхностей. Вокруг нее поворачивают другую поверхность так, чтобы общая плоскость симметрии 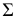
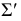
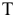
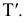
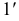
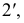
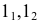
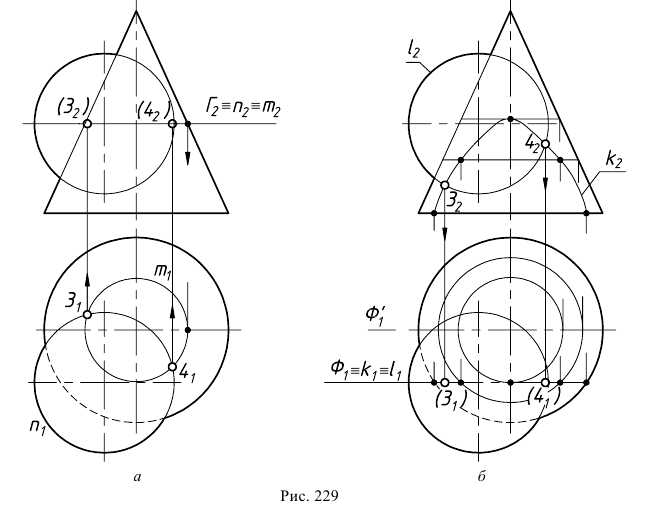
Как уже отмечалось, для определения точек изменения видимости плоскость проводят через очерк той поверхности, которая определяет видимость на соответствующей плоскости проекций. Так, на рис. 229 а, для нахождения точек изменения видимости на 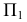
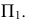
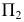
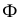
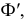
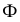
Пересечение многогранников
Линия пересечения двух многогранников может быть определена точками пересечения ребер одного многогранника с поверхностью другого и ребер второго с поверхностью первого способом вспомогательных секущих плоскостей.
Найденные точки пересечения соединяют в определенном порядке прямыми линиями, в результате чего получается замкнутая ломаная линия, звенья которой представляют собой линии пересечения граней обоих многогранников. Эта ломаная линия и будет являться линией пересечения.
При построении такой линии надо выполнять правило: соединять прямыми только те точки, которые лежат на одних и тех же гранях первого и второго многогранников. При определении видимости частей линии пересечения следует иметь в виду, что она будет видимой на проекциях только тех граней, которые видимы на данной проекции.
В зависимости от взаимного расположения пересекающихся поверхностей линия пересечения может представлять собой или одну замкнутую ломаную линию, или две. Построение линии пересечения двух многогранников на чертеже приведено ниже (VII.4., задача 7).
Способ вспомогательных секущих сфер
Для построения линии пересечения двух поверхностей вращения можно воспользоваться свойством, присущим поверхностям вращения: две соосные поверхности (т.е. поверхности с общей осью) пересекаются друг с другом по параллелям (окружностям), причем число последних равно числу точек пересечения меридианов поверхностей.
Действительно, пусть коническая поверхность образуется вращением образующей 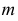
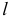
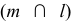
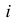
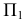
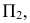
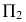
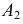
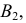
Аналогично, если расположить центр сферы на оси любой поверхности вращения, то сфера рассечет эту поверхность по окружностям, перпендикулярным оси вращения. Эти окружности (параллели) спроецируются на плоскость проекций в виде отрезков прямых, перпендикулярных проекции оси, только если ось рассекаемой поверхности вращения параллельна данной плоскости проекций.
С помощью вспомогательных поверхностей (сфер) сравнительно просто решаются задачи на построение линий пересечения двух произвольных поверхностей вращения, имеющих общую плоскость симметрии, при этом возможны два случая:
- — если оси поверхностей пересекаются, то для определения линии пересечения поверхностей используют семейство концентрических сфер, центр которых находится в точке пересечения осей поверхностей;
- — если оси не пересекаются, применяют эксцентрические сферы, центры которых перемещаются по оси одной из поверхностей.
Рассмотрим каждый случай в отдельности.
Построение линии пересечения двух поверхностей вращения с помощью концентрических сфер
Метод вспомогательных концентрических сфер можно применить при наличии следующих условий:
- пересекающиеся поверхности должны быть поверхностями вращения, так как сфера рассекает соосную с ней поверхность вращения по параллелям (окружностям);
- оси поверхностей вращения должны пересекаться, так как через точку пересечения осей можно провести сферу, соосную обеим данным поверхностям вращения;
- оси поверхностей вращения должны быть параллельны плоскости проекций, так как в этом случае параллели пересечения вспомогательной секущей сферы с данными поверхностями вращения будут проецироваться на эту плоскость проекций в виде отрезков прямых. Точки, общие для данных поверхностей, находятся как точки пересечения полученных параллелей (в виде отрезков прямых).
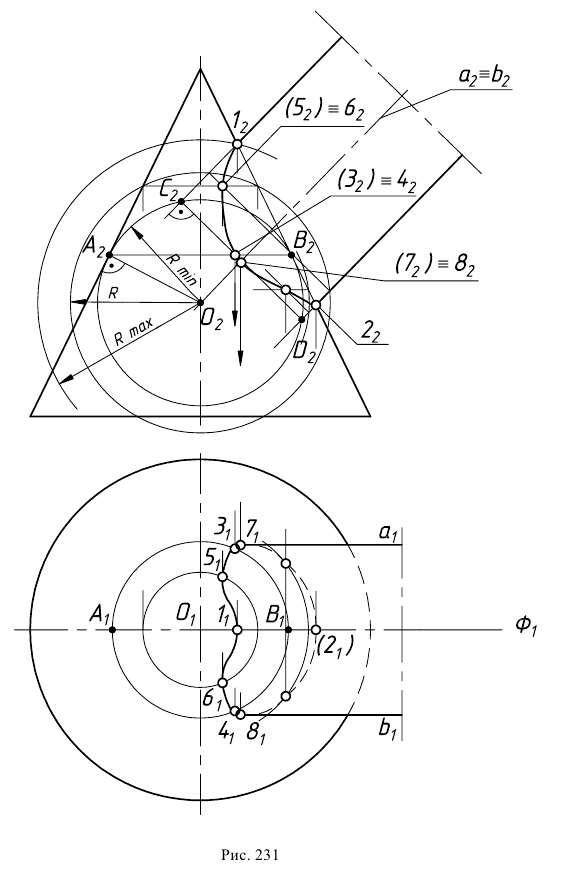
Рассмотрим основные этапы построения линии пересечения двух поверхностей — конуса и цилиндра вращения способом концентрических сфер (рис. 231).
Опорные точки 1 и 2, лежащие в плоскости симметрии 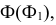
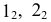
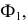
Далее выполняют следующие построения. Определяют центр 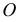
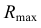
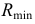
Радиус 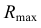
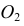
Радиус 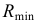
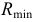
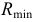
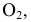
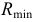
Сфера, как соосная с конусом и цилиндром, пересечет их по окружностям диаметрами 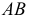
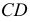
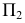
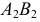
Рассмотрим взаимное расположение полученных линий пересечения (окружностей диаметрами 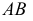
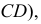
По линии проекционной связи находят горизонтальные проекции 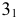
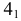
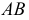
Проводя из точки 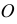
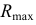
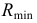
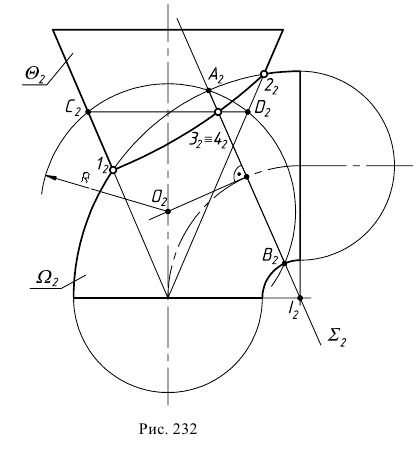
Точки изменения видимости 7 и 8 линии пересечения относительно плоскости 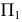
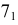
Построение линии пересечения двух поверхностей вращения с помощью эксцентрических сфер
Метод эксцентрических сфер применяется при построении линии пересечения поверхностей вращения с поверхностью, несущей на себе непрерывное множество окружностей. При этом обе поверхности должны иметь общую плоскость симметрии.
Вспомогательные эксцентрические сферы пересекаются с данными поверхностями по окружностям, которые проецируются на плоскость проекций, параллельную плоскости симметрии, в виде отрезков прямых.
Пример построения линии пересечения двух поверхностей вращения способом эксцентрических сфер рассмотрен на рис. 232, где кольцо 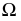
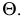
Круговые сечения конуса вращения получаются при сечении его плоскостями уровня. Кольцо имеет три системы круговых сечений, двумя из них мы воспользуемся в решении задачи. Одна система круговых сечений тора находится в плоскостях, перпендикулярных оси тора. Другая система находится в меридиональных плоскостях.
При построении линии пересечения прежде всего определяют точки 1 и 2, лежащие в общей плоскости симметрии заданных поверхностей. Затем через ось вращения тора проводим фронтально проецирующую плоскость 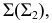
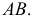
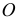
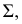
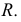
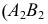
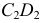
Аналогично определяем другие промежуточные точки линии пересечения поверхностей. Вспомогательные сферы имеют различные центры, находящиеся на оси конуса вращения.
По фронтальной проекции линии пересечения строят ее горизонтальную проекцию, используя принадлежности точек этой линии любой из поверхностей.
Частные случаи построения линии пересечения поверхностей. Теорема Монжа
Теорема. Если две поверхности второго порядка описаны (или вписаны) около третьей поверхности второго порядка, то они пересекаются между собой по двум плоским кривым второго порядка.
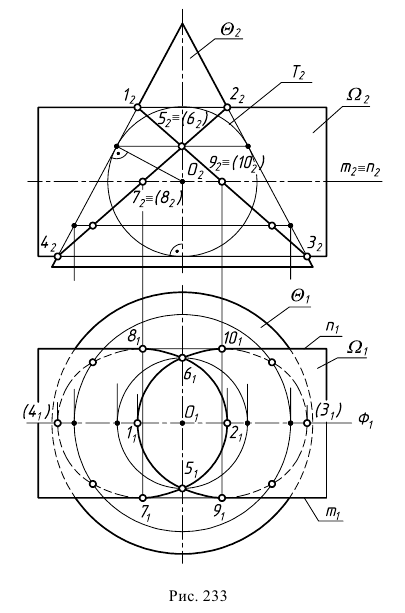
Пример построения линии пересечения поверхностей конуса 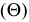
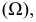
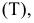
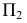
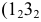
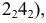
Имея фронтальные проекции линии пересечения поверхностей, можно легко построить их горизонтальные проекции (рис. 233).
Примеры решения задач
Задача 1. Построить линию пересечения пирамиды с горизонтально-проецирующей плоскостью 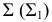
При пересечении пирамиды плоскостью получается ломаная линия.
Горизонтальная проекция линии пересечения совпадает с горизонтальным следом 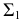
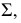
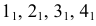
Видимость линии пересечения определяется в соответствии с видимостью граней пирамиды. Стороны линии пересечения, лежащие на видимых гранях, будут видимыми, а лежащие на невидимых гранях — невидимы.
Задача 2. Построить линию пересечения сферы с фронтально-проецирующей плоскостью (рис. 235).
При пересечении сферы плоскостью 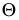
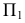
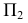
Для построения малой оси эллипса 12 на плоскости 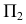
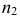
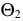
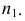
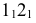
Большая и малая оси эллипсов перпендикулярны и делятся точкой пересечения пополам. Для построения большой оси эллипса отрезок 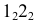
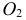
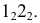
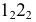
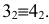
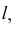
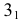
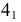
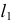
Точки изменения видимости искомой линии на 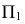
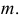
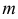
Для построения плавной кривой находятся промежуточные точки линии пересечения, как точки на соответствующих параллелях сферы.
Полученные точки линии пересечения соединяются с учетом видимости. На горизонтальной проекции линии пересечения будут видны точки, лежащие выше экватора в верхней половине сферы. Видимость поменяется на противоположную в точках 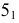
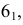
Натуральная величина сечения представляет собой окружность радиусом 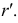
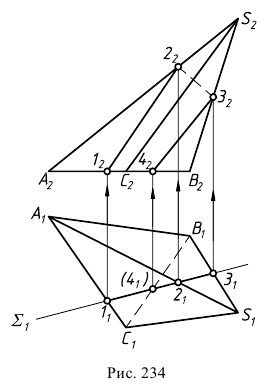
Задача 3. Построить сечение прямого кругового конуса плоскостью общего положения 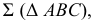
Анализ заданных геометрических образов показывает, что сечение поверхности вращения плоскостью является фигурой симметричной. Ось симметрии искомой линии пересечения лежит в плоскости 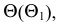
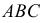
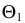
Кривая сечения строится по точкам способом вспомогательных секущих плоскостей. Построения начинаются с опорных точек.
Высшая и низшая точки, как правило, лежат в общей плоскости симметрии двух пересекающихся геометрических образов. Плоскость 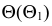
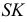
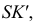
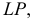
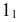
Низшие точки в данном примере располагаются на основании конуса в плоскости 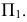
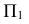
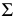
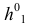
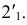
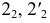
Точки изменения видимости строятся при помощи фронтальной плоскости уровня 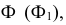
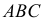
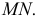
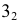
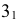
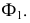
Промежуточные точки линии пересечения строятся при помощи вспомогательных плоскостей уровня 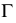
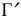
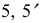
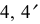
Для определения вида кривой, получающейся в сечении, выполняется перемена плоскостей проекций. Плоскость 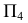
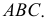
Натуральная величина сечения построена проецированием на дополнительную плоскость 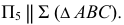
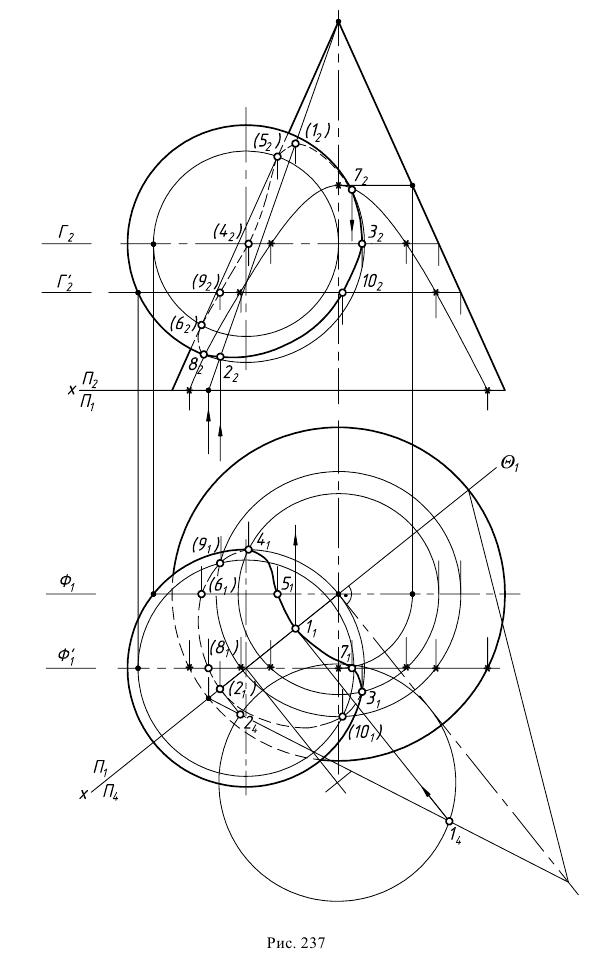
Задача 4. Построить линию пересечения сферы и прямого кругового конуса; проанализировать характерные точки линии; показать видимость линии пересечения и очерков поверхностей (рис. 237).
Анализ заданных г.о. показывает, что общая плоскость симметрии поверхностей 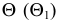
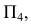
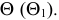
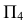
Для построения остальных точек искомой линии пересечения применяют способ вспомогательных секущих плоскостей.
Точки, лежащие на экваторе сферы (точки изменения видимости на 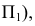
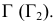
Точки искомой линии пересечения, лежащие на фронтальном очерке конуса, определяют при помощи фронтальной плоскости уровня Ф ( i), проходящей через ось конуса. При пересечении фронтальной проекции очерка конуса с соответствующей параллелью сферы получают точки 5 и 6.
Для определения точек линии пересечения, принадлежащих фронтальному очерку сферы, вводят секущую плоскость 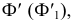
Промежуточные точки искомой линии пересечения строят при помощи секущей плоскости 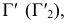
Построенные точки соединяют с учетом видимости поверхностей. На плоскости проекций 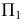
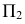
Искомая линия пересечения представляет собой пространственную кривую линию, расположенную на заданных поверхностях. Ее проекции на комплексном чертеже — плавные кривые линии, при этом на 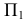
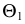
Задача 5. Построить линию пересечения конической поверхности и четверти торовой поверхности; проанализировать линию пересечения и ее проекции (рис. 238).
Решение задачи выполняем в следующей последовательности.
Сначала строим точки, расположенные в общей плоскости симметрии 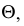
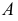
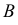
Затем находим точки изменения видимости на 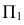
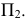
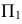
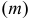
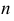
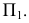
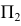
Предполагаемые точки изменения видимости могут принадлежать фронтальному очерку либо конической поверхности, либо торовой. С помощью плоскости 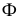
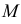
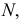
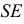
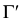
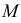
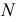
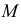
Промежуточные точки (см. рис. 227) определяем при помощи горизонтальных плоскостей уровня, рассекающих данные поверхности по параллелям. На рис. 238 обозначены проекции промежуточных точек 3 и 4, найденных с помощью плоскости 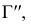
Все построенные точки соединяем с учетом видимости тех частей поверхностей, которым они принадлежат. Показываем видимость проекций очерков: толстой линией — видимые очерки, тонкой штриховой линией — невидимые очерки, очерки поверхностей, пропадающие друг в друге -тонкой сплошной линией. Построенная линия представляет собой симметричную замкнутую кривую линию четвертого порядка.
Проекции искомой линии являются плоскими кривыми (второго порядка), при этом горизонтальная проекция линии перехода симметрична относительно следа 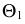
Задача 6. Построить линию пересечения трехгранной призмы и прямого кругового конуса (рис. 239).
Анализ заданных геометрических образов показывает, что грани призмы пересекают коническую поверхность по кривым 2-го порядка.
Вид этих кривых определяют переменой плоскостей проекций, выбирая вспомогательную плоскость проекций так, чтобы грани призмы заняли проецирующее положение. Плоскость проекций 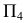
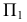
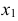
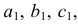
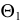
Для построения искомой линии пересечения целесообразно применять способ вспомогательных секущих плоскостей частного положения.
Линия пересечения грани 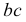
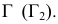
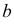
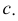
Для построения точек, лежащих на фронтальном очерке конуса, вводят секущую плоскость 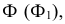
Вершины эллипса 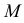
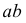
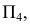
Промежуточные точки искомой линии пересечения строят при помощи вспомогательных горизонтальных плоскостей уровня, рассекающих конус по параллелям, а призму — по образующим. На рис. 239 обозначены проекции промежуточных точек 9, 10, 11, 12, найденных с помощью плоскости 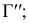
Построенные точки соединяют с учетом видимости тех частей поверхностей, которым они принадлежат. На плоскости проекций 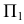
После построения проекций линии пересечения показывают видимость очерков поверхностей.
Задача 7. Построить линию пересечения многогранников: шестигранной горизонтально-проецирующей призмы I и трехгранной наклонной призмы II (рис. 240).
Точки (1, 2, 3, 4, 5, 6), принадлежащие линии пересечения многогранников, получаем непосредственно без вспомогательных построений, как точки, в которых боковые ребра 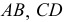
Далее находим точки пересечения ребер 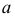
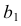
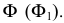
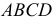
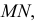
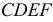
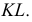
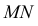
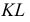
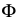
Точки пересечения ребер 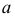
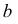
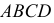
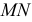
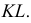
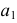
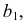
Точки 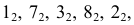
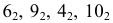
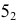
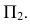
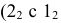
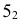
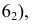
Точки 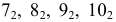
Горизонтальные проекции линий пересечения совпадают с горизонтальными следами тех боковых граней призмы I, которым отрезки ломаной линии соответственно принадлежат.
После построения линии пересечения обводим ребра обоих многогранников, учитывая их видимость относительно друг друга.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
- Решение метрических задач
- Взаимное расположение геометрических образов и фигур
- Преобразование чертежа
- Кривые линии
- Образование и задание поверхности на чертеже
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнение плоскости, виды уравнения плоскости
В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.
Определение уравнения плоскости
Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.
Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.
Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.
Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.
Общее уравнение плоскости
Сформулируем теорему, а затем запишем уравнение плоскости.
Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве
Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.
Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.
Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.
Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .
Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.
Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.
Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .
Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.
Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.
Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.
Нормальное уравнение плоскости
Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .
Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.
n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1
То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.
Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.
Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.
Уравнение плоскости в отрезках
Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .
Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.
Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .
Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.
http://www.evkova.org/peresechenie-poverhnosti-ploskostyu-i-pryamoj
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-vidy-uravnenija-ploskosti/




































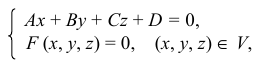
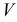
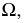 которую выбирают так, чтобы она пересекла поверхность по графически простым линиям (прямым или окружностям);
которую выбирают так, чтобы она пересекла поверхность по графически простым линиям (прямым или окружностям);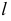 и
и 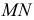 пересечения вспомогательной секущей плоскости
пересечения вспомогательной секущей плоскости 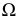 с поверхностью
с поверхностью 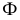 и плоскостью
и плоскостью 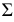 соответственно;
соответственно;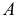 и
и 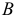 взаимного пересечения линий
взаимного пересечения линий 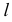 и
и 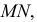 лежащих в секущей плоскости
лежащих в секущей плоскости 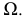 Точки
Точки 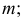
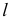 от оси тора.
от оси тора.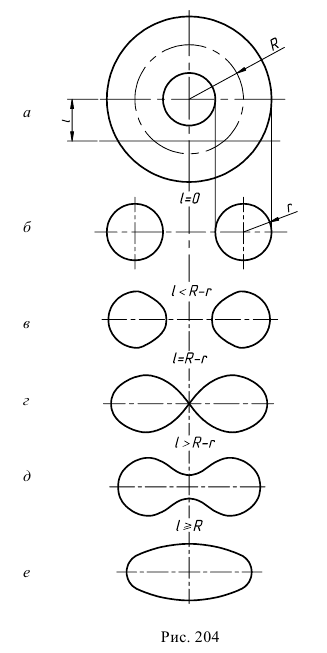
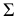
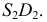
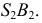
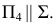
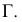
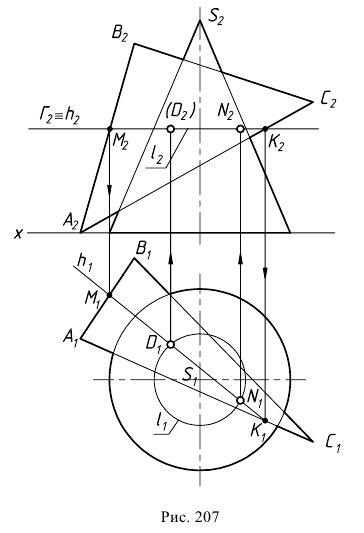
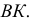
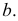
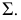
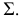
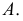
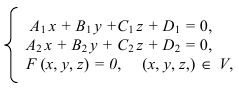
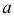 проводится вспомогательная плоскость
проводится вспомогательная плоскость 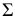 (рис.216);
(рис.216);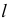 вспомогательной плоскости
вспомогательной плоскости 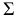 с данной поверхностью
с данной поверхностью 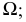
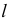 с заданной прямой а найдутся искомые точки
с заданной прямой а найдутся искомые точки 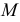 и
и 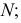
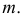
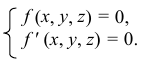
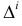 относительно данных поверхностей
относительно данных поверхностей 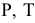 такими, чтобы в пересечении получались графически простые линии (прямые, окружности), и проекции этих линий легко строились на эпюре;
такими, чтобы в пересечении получались графически простые линии (прямые, окружности), и проекции этих линий легко строились на эпюре;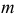 и
и 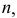 по которым посредник пересечет обе поверхности;
по которым посредник пересечет обе поверхности;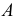 и
и 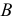 пересечения линий
пересечения линий 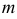 и
и 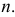 Эти точки принадлежат одному посреднику и одновременно двум данным поверхностям;
Эти точки принадлежат одному посреднику и одновременно двум данным поверхностям;