Сферическая система координат уравнение сферы

Формулы аналитической геометрии в пространстве

$d=\sqrt<(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2>$

НАПРАВЛЯЮЩИЙ КОСИНУС ЛИНИИ, СОЕДИНЯЮЩЕЯ ТОЧКИ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$
$l=\cos\alpha=\frac<(x_2-x_1)>$, $m=\cos\beta=\frac$, $n=\cos\gamma=\frac$

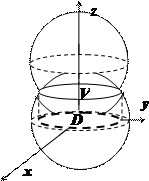
где $\alpha,\beta,\gamma$ углы, которые линия $P_1P_2$ образовывает с положительными осями $x,y,z$ соответственно, а $d$ определено на рисунке вверху.

ОТНОШЕНИЕ МЕЖДУ НАПРЯВЛЯЮЩИМИ КОСИНУСАМИ
$\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$ или $l^2+m^2+n^2=1$

НАПРАВЛЯЮЩИЕ ЧИСЛА
Числа $L,M,N$, которые есть пропорциональны к направляющим косинусам $l, m, n$ называются направляющими числами. Отношение между ними

Это также действительно, если $l, m, n$ заменяются на $L, M, N$ соответственно.

УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
$x=x_1+lt$, $y=y_1+mt$, $z=z_1+nt$

Это также действительно если $l, m, n$ заменяются на $L, M, N$ соответственно.

УГОЛ $\phi$ МЕЖДУ ДВУМЯ ЛИНЯМИ С НАПРАВЛЯЮЩИМИ КОСИНУСАМИ $l_1, m_1, n_1$ И $l_2, m_2, n_2$
$\cos\phi=l_1l_2+m_1m_2+n_1n_2$

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
$Ax + By + Cz + D = 0$ [$A, B, C, D$ — константы]

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ $(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$

$\beginx-x_1 & y-y_1 & z-z_1\\ x_2-x_1 & y_2-y_1 & z_2-z_1\\ x_3-x_1 & y_3-y_1 & z_3-z_1\end=0$

$\begin y_2-y_1 & z_2-z_1\\ y_3-y_1 & z_3-z_1\end(x-x_1)$ $+\begin z_2-z_1 & x_2-x_1\\ z_3-z_1 & x_3-x_1\end(y-y_1)$ $+\begin x_2-x_1 & y_2-y_1\\ x_3-x_1 & y_3-y_1\end(z-z_1)=0$

где $a, b, c$ есть пересечения на осях $x, y, z$ соответственно.

Обратите внимание, что направляющие числа для линии, перпендикулярной к плоскости $Ax + By + Cz + D = 0$ есть $A, B, C$.

где знак выбирается так, что расстояние не является отрицательным.

НОРМАЛЬНОЕ УРАВНЕНИЯ ПЛОСКОСТИ
$x\cos\alpha+y\cos\beta+z\cos\gamma=p$

где $p$ = перпендикулярному расстоянию от $O$ к плоскости в $P$ и $\alpha, \beta, \gamma$ есть углами между $OP$ и положительными осями $x, y, z$.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ
$\left\<\beginx=x’+x_0\\ y=y’+y_0\\ z=z’+z_0\end\right.$ $\left\<\beginx’=x-x_0\\ y’=y-y_0\\ z’=z-z_0\end\right.$

где $(x, y, z)$ — старые координаты [т.e. координаты относительно системы xyz], $(x’, y’, z’)$ — новые координаты [относительно системы $x’y’z’$] и $(x_0,y_0,z_0)$ координаты нового центра $O’$ относительно старой координатной системы $xyz$.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ВРАЩЕНИИ

где центры систем $xyz$ и $x’y’z’$ находятся в одной точке и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ И ВРАЩЕНИИ

$\left\<\beginx=l_1x’+l_2y’+l_3z’+x_0\\ y=m_1x’+m_2y’+m_3z’+y_0\\ z=n_1x’+n_2y’+n_3z’+z_0\end\right.$

$\left\<\beginx’=l_1(x-x_0)+m_1(y-y_0)+n_1(z-z_0)\\ y’=l_2(x-x_0)+m_2(y-y_0)+n_2(z-z_0)\\ z’=l_3(x-x_0)+m_3(y-y_0)+n_3(z-z_0)\end\right.$

где $O’$ системы $x’y’z’$ имеет координаты $(x_0,y_0,z_0)$ относительно системы $xyz$ и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.

ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ $(r, \theta, z)$
Точка $P$ может быть определена как цилиндрическими координатами $(r, \theta, z)$, так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя координатами есть

СФЕРИЧЕСКИЕ КООРДИНАТЫ $(r, \theta, \phi)$
Точка $P$ может быть определена как сферическими координатами $(r, \theta, \phi)$ так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя кординатами есть

$\left\<\beginx=r\sin\theta\cos\phi\\ y=r\sin\theta\sin\phi\\ z=r\cos\theta\end\right.$

УРАВНЕНИЕ СФЕРЫ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
$(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$

где сфера имеет центр $(x_0,y_0,z_0)$ и радиус $R$.

УРАВНЕНИЕ СФЕРЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
$r^2-2r_0r(\theta-\theta_0)+r_0^2+(z-z_0)^2=R^2$

где сфера имеет центр $(r_0;\theta_0;z_0)$ в цилиндрических координатах и радиус $R$.

Если центр находится в начале координат, уравнение имеет вид:

УРАВНЕНИЕ СФЕРЫ В СФЕРИЧЕСКИХ КООРДИНАТАХ
$r^2+r_0^2-2r_0 r\sin\theta\sin\theta_0\cos(\phi-\phi_0)=R^2$

где сфера имеет центр $(r_0; \theta_0; \phi_0)$ в сферических координатах и радиус $R$.

Если центр в начале координат, уравнение имеет вид:

ЭЛЛИПТИЧЕСКИЙ ЦИЛИНДР С ОСЬЮ КАК $z$ ОСЬ
$\frac+\frac=1$

где $a, b$ — полуоси эллиптического сечения.
Если $b = a$, фигура превращается в цилиндрический цилиндр с радиусом $a$.

Обратите внимание на ориентацию осей этой фигуры.

Сферические координаты (сферическая система координат)

Для введения сферической системы координат в пространстве выбирается плоскость ( основная плоскость ) и на ней задается полярная система координат с полюсом ( начало сферической системы координат ) и полярной осью . Через точку перпендикулярно основной плоскости проведем ось ( ось аппликат ) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси происходило против часовой стрелки (рис.2.36,а).

В сферической системе координат положение точки , не лежащей на оси аппликат, характеризуется расстоянием до начала координат, полярным углом точки — ортогональной проекции точки на основную плоскость, и углом между вектором и положительным направлением оси аппликат. Таким образом, сферические координаты точки — это упорядоченная тройка чисел – радиус , долгота и широта . У точек, принадлежащих оси аппликат, не определена долгота, их положение задается радиусом и широтой для положительной части оси и для отрицательной ее части. Начало координат задается нулевым значением радиуса . Иногда вместо угла широтой называют угол , принимающий значения .

Со сферической системой координат можно связать прямоугольную систему координат (рис.2.36,б), у которой начало и базисные векторы совпадают с началом сферической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат ( связанную с данной прямоугольной ).

Переход от сферических координат к декартовым (прямоугольным)

Получим формулы, связывающие между собой прямоугольные координаты точки и её сферические координаты . По рис.2.36,б получаем

Эти формулы перехода позволяют найти прямоугольные координаты по известным сферическим координатам. Обратный переход выполняется по формулам

Формулы (2.22) определяют долготу с точностью до слагаемых , где . При из них следует, что . Главное значение долготы находится по формулам (см. рис.2.29).

Пример 2.13. В сферической системе координат :

а) построить координатные поверхности ;

б) найти сферические координаты точки , если известны её прямоугольные координаты ;

в) найти прямоугольные координаты точки , если известны её сферические координаты: .

Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении радиуса , является сфера с центром в начале координат (рис.2.37). Этим объясняется название сферической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении долготы , является полуплоскость, ограниченная осью аппликат (на рис.2.37 изображена полуплоскость ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении широты , является конус, ось которого совпадает с осью аппликат, а вершина — с началом координат. При получаем основную плоскость. На рис.2.37 изображены конус и основная плоскость .

б) Найдем сферические координаты точки . По формулам (2.22), учитывая рис.2.29 (см. пример 2.12), получаем

Примеры применения цилиндрических и сферических координат

Примеры применения цилиндрических и сферических координат

1. Услуги проектирования
2. Тройной интеграл
3. Примеры применения цилиндрических и сферических координат

Примеры применения цилиндрических и сферических координат

Как и в случае перехода к полярным координатам в двойном интеграле, дать однозначный рецепт того, когда следует применять цилиндрические или сферические координаты, нельзя, это дело опыта. Можно попробовать применить цилиндрические координаты, если подынтегральная функция и/или уравнения поверхностей, ограничивающих объём $\mathbf < \textit < V >> $, зависят от комбинации $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >=\mathbf < \textit < r >> ^ < 2 >$; сферические — если эти уравнения зависят от $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >=\mathbf < \textit < r >> ^ < 2 >$. Рассмотрим ряд примеров.

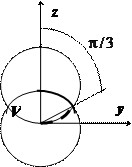
Найти объём $\mathbf < \textit < V >> $ общей части двух шаров, ограниченных сферами

Решение:

Пересечение сфер находится на уровне $2Rz=R^2\Rightarrow z=R/2$ и представляет собой круг радиуса $R\frac < \sqrt 3 > < 2 >$. Объём $\mathbf < \textit < V >> $ограничен сверху поверхностью $z=\sqrt < R^2-x^2-y^2 >$, снизу — поверхностью $z=R-\sqrt < R^2-x^2-y^2 >$. Вычисления в декартовых координатах дают $V=\iiint\limits_V < dv >=\iiint\limits_V < dxdydz >=\int\limits_ < -R\frac < \sqrt 3 > < 2 >> ^ < R\frac < \sqrt 3 > < 2 >> < dx\int\limits_ < -\sqrt < \frac < 3 > < 4 >R^2-x^2 > > ^ < \sqrt < \frac < 3 > < 4 >R^2-x^2 > > < dy\int\limits_ < R-\sqrt < R^2-x^2-y^2 >> ^ < \sqrt < R^2-x^2-y^2 >> < dz >> > $ — достаточно громоздкие выкладки.

В цилиндрических координатах объём $\mathbf < \textit < V >> $ ограничен сверху поверхностью $z=\sqrt < R^2-r^2 >$, снизу — поверхностью $z=R-\sqrt < R^2-r^2 >$, поэтому

В сферических координатах уравнение нижней сферы принимает вид $r=R$, верхней — $r^2=2Rr\cos \theta \Rightarrow r=2R\cos \theta $, их пересечение соответствует значению $\cos \theta =1/2\Rightarrow \theta =\pi /3$. В интервале $0\leqslant \theta \leqslant \pi /3 \quad \mathbf < \textit < r >> $ меняется от $0$ до $\mathbf < \textit < R >> $, в интервале $\pi /3\leqslant \theta \leqslant \pi /2 \quad \mathbf < \textit < r >> $ меняется от $0$ до $2R\cos \theta $, поэтому

В этом примере трудоёмкость вычислений в цилиндрических и сферических координатах примерно одинакова.

Решение:

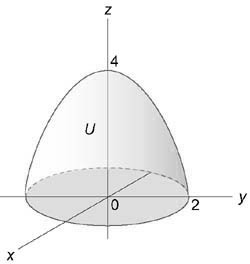
Параболоид и конус пересекаются в плоскости $x=2-x^2\Rightarrow x=1$ по кругу радиуса 1. Осью симметрии объёма $\mathbf < \textit < V >> $ служит ось $\mathbf < \textit < Ох >> $, поэтому цилиндрические координаты вводим формулами $x=x,\quad y=r\cos \varphi ,\quad z=r\sin \varphi ; \quad I=\iiint\limits_V < (x+y+z)dxdydz >=\iiint\limits_V < (x+r\cos \varphi +r\sin \varphi )rdxdrd\varphi >=\int\limits_0^ < 2\pi > < d\varphi \int\limits_0^1 < rdr\int\limits_r^ < 2-r^2 > < (x+r\cos \varphi +r\sin \varphi )dx >> > =$ $ =\int\limits_0^ < 2\pi > < d\varphi \int\limits_0^1 < \left. < \frac < x^2 > < 2 >>\right|_r^ < 2-r^2 >rdr > > +\int\limits_0^ < 2\pi > < (\cos \varphi +\sin \varphi )d\varphi \int\limits_0^1 < \left. x \right|_r^ < 2-r^2 >r^2dr > > =\pi \int\limits_0^1 < \left( < 4-5r^2+r^4 >\right)dr > =\frac < 38\pi > < 15 >. $ Применение сферических координат в этом примере нецелесообразно < громоздкое уравнение для параболоида >.

Решение:

Здесь область интегрирования — шар радиуса 1/2, сдвинутый по оси $\mathbf < \textit < Оz >> $ на 1/2 единицы, подынтегральная функция зависит от выражения $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >$, поэтому применим сферические координаты. Уравнение сферы $x^2+y^2+z^2=z\Rightarrow r^2=r\cos \theta \Rightarrow r=\cos \theta \left( < \Rightarrow 0\leqslant \theta \leqslant \pi /2 >\right)$ , поэтому $I=\iiint\limits_V < \sqrt < x^2+y^2+z^2 >dxdydz > =\iiint\limits_V < r\cdot r^2\sin \theta drd\varphi d\theta >=\int\limits_0^ < 2\pi > < d\varphi \int\limits_0^ < \pi /2 > < \sin \theta d\theta >\int\limits_0^ < \cos \theta > < r^3dr >> =\frac < 2\pi > < 4 >\int\limits_0^ < \pi /2 >< \left. < r^4 >\right|_0^ < \cos \theta >\sin \theta d\theta > = \\ =\frac < 2\pi > < 4 >\int\limits_0^ < \pi /2 > < \cos ^4\theta \sin \theta d\theta >=-\frac < 2\pi > < 4\cdot 5 >\left. < \cos ^5\theta >\right|_0^ < \pi /2 >=\frac < \pi > < 10 >$.

Вычислить объём тела, ограниченного поверхностью $\left( < x^2+y^2+z^2 >\right)^ < \,2 >=a^3z,\;a=const>0$

Решение:

Здесь тоже для того, чтобы понять, как устроено тело, и найти его объём, надо перейти к сферическим координатам < на это указывает комбинация $\mathbf < \textit < x >> ^ < 2 >+\mathbf < \textit < y >> ^ < 2 >+\mathbf < \textit < z >> ^ < 2 >=\mathbf < \textit < r >> ^ < 2 >)$. Уравнение поверхности $\left( < x^2+y^2+z^2 >\right)^ < \,2 >=a^3z\Rightarrow r^4=a^3r\cos \vartheta \Rightarrow r=a\sqrt[3] < \cos \vartheta >\;\left( < \Rightarrow 0\leqslant \theta \leqslant \pi /2 >\right)$. По этому уравнению поверхность построить уже можно; отсутствие координаты $\varphi $ в уравнении показывает, что это — тело вращения вокруг оси $\mathbf < \textit < Oz >> $. Находим объём: $ V=\iiint\limits_V < r^2\sin \theta drd\varphi d\theta >=\int\limits_0^ < 2\pi > < d\varphi \int\limits_0^ < \pi /2 > < \sin >> \theta d\theta \int\limits_0^ < a\sqrt[3] < \cos \theta >> < r^2dr >=\frac < 2\pi > < 3 >\int\limits_0^ < \pi /2 >< \left. < r^3 >\right|_0^ < a\sqrt[3] < \cos \theta >> \sin \theta d\theta = > $ $ =\frac < 2\pi a^3 > < 3 >\int\limits_0^ < \pi /2 > < \cos \theta \sin \theta d\theta = >\frac < \pi a^3 > < 3 >. $

Вычислить интеграл $\iiint\limits_U < \left( < < x^4 >+ 2 < x^2 > < y^2 >+ < y^4 >>\right)dxdydz > ,$ где область (U) ограничена поверхностью ( < x^2 >+ < y^2 >\le 1) и плоскостями (z = 0,) (z = 1).

Решение:

Данный интеграл удобно вычислить в цилиндрических координатах. Проекция области интегрирования на плоскость (Oxy) представляет собой круг ( < x^2 >+ < y^2 >\le 1) или (0 \le \rho \le 1).

Заметим, что подынтегральное выражение записывается в виде $ < \left( < < x^4 >+ 2 < x^2 > < y^2 >+ < y^4 >>\right) > = < < \left( < < x^2 >+ < y^2 >>\right)^2 > > = < < \left( < < \rho ^2 >>\right)^2 > = < \rho ^4 >> $

Тогда интеграл будет равен $I = \int\limits_0^ < 2\pi > < d\varphi >\int\limits_0^1 < < \rho ^4 >\rho d\rho > \int\limits_0^1 < dz >.$

Здесь во втором интеграле добавлен множитель (\rho) якобиан преобразования декартовых координат в цилиндрические. Все три интеграла по каждой из переменной не зависят друг от друга.

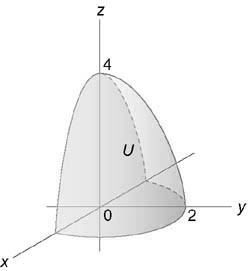
Вычислить интеграл $\iiint\limits_U < \left( < < x^2 >+ < y^2 >>\right)dxdydz > ,$ где область (U) ограничена поверхностями ( < x^2 >+ < y^2 >= 3z,) (z = 3)

Решение:

Область интегрирования изображена на рисунке

Для вычисления интеграла перейдем к цилиндрическим координатам: $ < x = \rho \cos \varphi , >\;\; < y = \rho \sin \varphi , >\;\; < z = z. >$ Дифференциал при этом равен $dxdydz = \rho d\rho d\varphi dz\;\;\left( < \rho - \text < якобиан >>\right).$

Уравнение параболической поверхности принимает вид: $ < \rho ^2 > < \cos ^2 >\varphi + < \rho ^2 > < \sin^2 >\varphi = 3z\;\;\text < или >\;\; < \rho ^2 >= 3z.$ Проекция области интегрирования (U) на плоскость (Oxy) представляет собой окружность ( < x^2 >+ < y^2 >\le 9) радиусом (\rho = 3).

Координата (\rho) изменяется в пределах от (0) до (3,) угол (\varphi) от (0) до (2\pi) и координата (z) от (\large\frac < < < \rho ^2 >> > < 3 >\normalsize) до (3.)

Используя цилиндрические координаты, найти значение интеграла $ I = \int\limits_ < - 2 >^2 < dx >\int\limits_ < - \sqrt < 4 - < x^2 >> > ^ < \sqrt < 4 - < x^2 >> > < dy >\int\limits_0^ < 4 - < x^2 >— < y^2 >> < < y^2 >dz > $

Решение:

Область интегрирования (U) изображена на рисунке:

Ее проекция на плоскость (Oxy) представляет собой круг ( < x^2 >+ < y^2 >= < 2^2 >):

Новые переменные в цилиндрических координатах будут изменяться в пределах $ < 0 \le \rho \le 2, >\;\; < 0 \le \varphi \le 2\pi , >\;\; < 0 \le z \le 4 - < \rho ^2 >. > $

Вычислить интеграл, используя цилиндрические координаты: $\iiint\limits_U < \sqrt < < x^2 >+ < y^2 >> dxdydz > .$ Область (U) ограничена параболоидом (z = 4 — < x^2 >— < y^2 >,) цилиндром ( < x^2 >+ < y^2 >= 4) и плоскостями (y = 0,) (z = 0)

Решение:

Изобразив схематически область интегрирования (U,) находим, что ее проекция на плоскость (Oxy) < область (D) >представляет собой полукруг радиусом (\rho = 2).

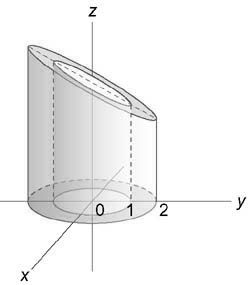
Найти интеграл $\iiint\limits_U < ydxdydz >,$ где область (U) ограничена плоскостями (z = x + 1,) (z = 0) и цилиндрическими поверхностями ( < x^2 >+ < y^2 >= 1,) ( < x^2 >+ < y^2 >= 4)

Решение:

Вычислим данный интеграл в цилиндрических координатах. Из условия $0 \le z \le x + 1$ следует, что $0 \le z \le \rho \cos \varphi + 1.$ Область интегрирования в плоскости (Oxy) представляет собой кольцо, ограниченное окружностями ( < x^2 >+ < y^2 >= 1) и ( < x^2 >+ < y^2 >= 4)

Следовательно, переменные (\rho) и (\varphi) изменяются в интервале $1 \le \rho \le 2,\;\;0 \le \varphi \le 2\pi .$

Этот результат закономерен, поскольку область (U) симметрична относительно плоскости (Oxz,) а подынтегральная функция является четной.

Найти интеграл (\iiint\limits_U < \sqrt < < x^2 >+ < y^2 >+ < z^2 >> dxdydz > ,) где область интегрирования (U) шар, заданный уравнением ( < < x^2 >+ < y^2 >+ < z^2 >> = 25.)

Решение:

Поскольку область (U) представляет собой шар, и к тому же подынтегральное выражение является функцией, зависящей от $f\left( < < x^2 >+ < y^2 >+ < z^2 >>\right),$ то перейдем к сферическим координатам.

Вычислить интеграл $\iiint\limits_U < < e^ < < < \left( < < x^2 >+ < y^2 >+ < z^2 >>\right) > ^ < \frac < 3 > < 2 >> > > > dxdydz > ,$ где область (U) представляет собой единичный шар ( < < x^2 >+ < y^2 >+ < z^2 >> \le 1.)

Решение:

Центр данного шара расположен в начале координат. Следовательно, в сферических координатах область интегрирования (U) описывается неравенствами $ < 0 \le \rho \le 1, >\;\; < 0 \le \varphi \le 2\pi , >\;\; < 0 \le \theta \le \pi . >$

Как видно, тройной интеграл вырождается в произведение трех однократных интегралов, каждый из которых вычисляется независимо. В результате находим $ < I = \int\limits_0^ < 2\pi > < d\varphi >\int\limits_0^1 < < e^ < < \rho ^3 >> > < \rho ^2 >d\rho > \int\limits_0^\pi < \sin \theta d\theta >> = < \left[ < \left. \varphi \right|_0^ < 2\pi >>\right] \cdot \int\limits_0^1 < \left( < < e^ < < \rho ^3 >> > \cdot \frac < 1 > < 3 >d < \rho ^3 >>\right) > \cdot \left[ < \left. < \left( < - \cos \theta >\right) >\right|_0^\pi >\right] > = < 2\pi \cdot \frac < 1 > < 3 >\left[ < \left. < \left( < < e^ < < \rho ^3 >> > >\right) >\right|_ < < \rho ^3 >= 0 > ^ < < \rho ^3 >= 1 > >\right] \cdot \left( < - \cos \pi + \cos 0 >\right) > = < \frac < < 2\pi >> < 3 >\cdot \left( < e - 1 >\right) \cdot 2 > = < \frac < < 4\pi >> < 3 >\left( < e - 1 >\right). > $

Вычислить интеграл (\iiint\limits_U < xyzdxdydz >,) где область (U) представляет собой часть шара ( < x^2 >+ < y^2 >+ < z^2 >\le < R^2 >,) расположенную в первом октанте (x \ge 0, y \ge 0, z \ge 0.)

Решение:

Найти тройной интеграл $\iiint\limits_U < \left( < \frac < < < x^2 >> > < < < a^2 >> > + \frac < < < y^2 >> > < < < b^2 >> > + \frac < < < z^2 >> > < < < c^2 >> > >\right)dxdydz > ,$ где область (U) ограничена эллипсоидом $ < \frac < < < x^2 >> > < < < a^2 >> > + \frac < < < y^2 >> > < < < b^2 >> > + \frac < < < z^2 >> > < < < c^2 >> > > = 1.$

Решение:

Для вычисления интеграла перейдем к обобщенным сферическим координатам путем следующей замены переменных: $ < x = a\rho \cos \varphi \sin \theta , >\;\; < y = b\rho \sin \varphi \sin \theta , >\;\; < z = c\rho \cos \theta . >$ Модуль якобиана данного преобразования равен (\left| I \right| = abc < \rho ^2 >\sin \theta .) Поэтому для дифференциалов справедливо соотношение $dxdydz = abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta .$ В новых координатах интеграл принимает вид: $ < I = \iiint\limits_U < \left( < \frac < < < x^2 >> > < < < a^2 >> > + \frac < < < y^2 >> > < < < b^2 >> > + \frac < < < z^2 >> > < < < c^2 >> > >\right)dxdydz > > = < \iiint\limits_ < U' >< \left[ < \frac < < < < \left( < a\rho \cos \varphi \sin \theta >\right) > ^2 > > > < < < a^2 >> > + \frac < < < < \left( < b\rho \sin \varphi \sin \theta >\right) > ^2 > > > < < < b^2 >> > + \frac < < < < \left( < c\rho \cos \theta >\right) > ^2 > > > < < < c^2 >> > >\right]abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta > > = \\ = < \iiint\limits_ < U' > < \left[ < < \rho ^2 > < < \cos >^2 > \varphi \, < < \sin >^2 > \theta + < \rho ^2 > < \sin^2 >\varphi \, < < \sin >^2 > \theta + < \rho ^2 > < < \cos >^2 > \theta >\right]abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta > > = \\ = < \iiint\limits_ < U' > < \left[ < < \rho ^2 > < < \sin >^2 > \theta \underbrace < \left( < < < \cos >^2 > \varphi + < \sin^2 >\varphi >\right) > _1 + < \rho ^2 > < < \cos >^2 > \theta >\right]abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta > > = \\ = < \iiint\limits_ < U' > < < \rho ^2 >\underbrace < \left( < < \sin^2 >\theta + < < \cos >^2 > \theta >\right) > _1abc < \rho ^2 >\sin \theta d\rho d\varphi d\theta > > = < abc\iiint\limits_ < U' > < < \rho ^4 >\sin \theta d\rho d\varphi d\theta > . > $

Вычислить интеграл $\int\limits_0^1 < dx >\int\limits_0^ < \sqrt < 1 - < x^2 >> > < dy >\int\limits_0^ < \sqrt < 1 - < x^2 >— < y^2 >> > < < < \left( < < x^2 >+ < y^2 >+ < z^2 >>\right) > ^2 > dz > ,$ используя сферические координаты.

Решение:

Область интегрирования представляет собой часть шара, расположенная в первом октанте и, следовательно, ограничена неравенствами $ < 0 \le \rho \le 1, >\;\; < 0 \le \varphi \le \frac < \pi > < 2 >, > \;\; < 0 \le \theta \le \frac < \pi > < 2 >. > $

Далее:

Формула Гаусса — Остроградского

Класс $S$. Теорема о замкнyтости класса $S$

Поток векторного поля через поверхность

Класс M. Теорема о замкнутости класса M

Несобственные интегралы по неограниченной области

Логические операции над высказываниями

Специальные векторные поля

Вычисление объёмов

Вычисление площади поверхности

Выражение площади плоской области через криволинейный интеграл

Вычисление криволинейного интеграла второго рода. Примеры.

Вычисление поверхностного интеграла первого рода

Теорема о предполных классах

Равносильные формулы алгебры высказываний

Огравление $\Rightarrow $