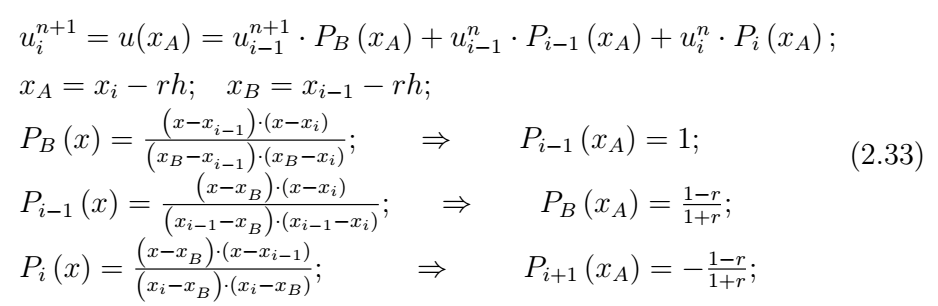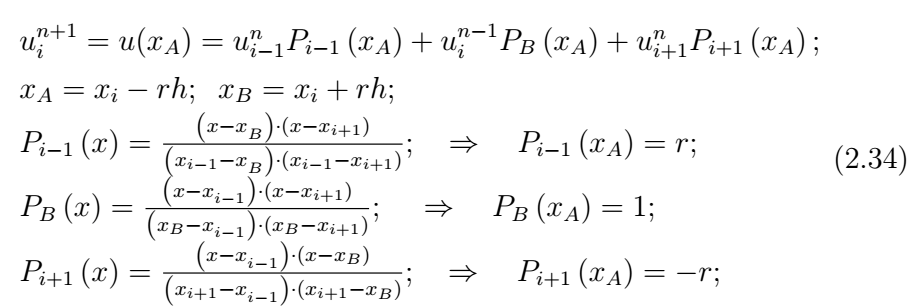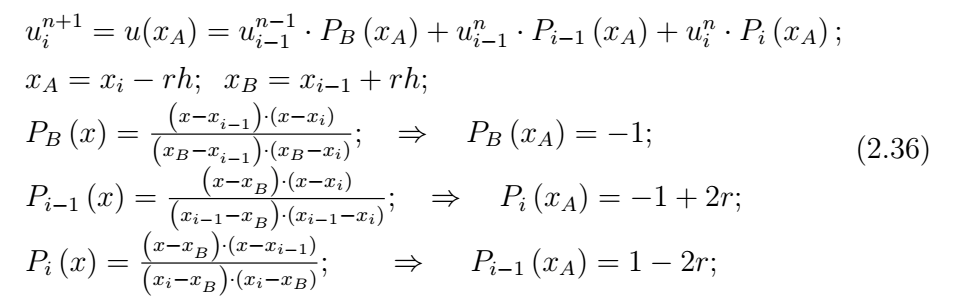Схема лакса для уравнения переноса

Схема лакса для уравнения переноса

2.4. Интерполяционно-характеристический метод (метод обратной характеристики)

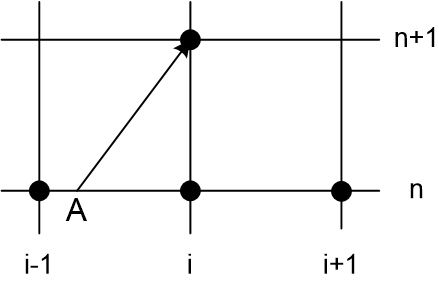
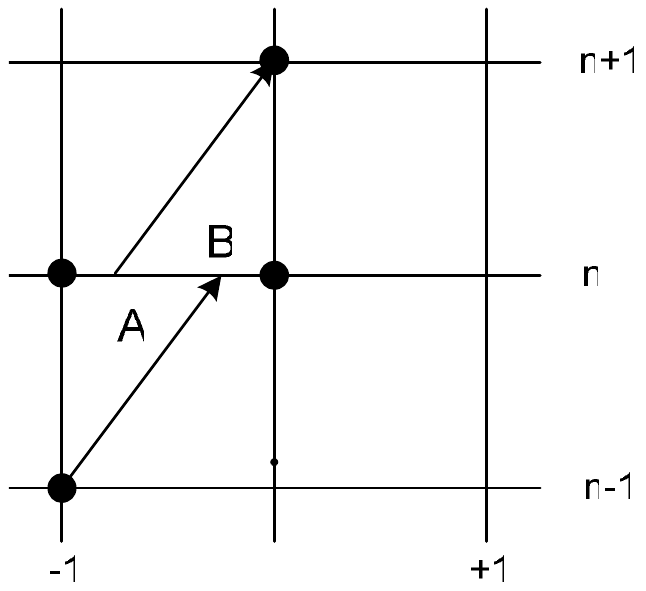
Более наглядный и менее затратный способ построения дискретных операторов для гиперболических уравнений связан с геометрической интерпретацией их решений. Известно, что решение дифференциального оператора переноса (2.1) остается постоянным на характеристиках — прямых линиях на плоскости \(\left(x,t\right)\), с коэффициентом наклона \(k=<\Delta t\mathord<\left/ <\vphantom <\Delta t \Delta x>> \right. > \Delta x> =<1\mathord<\left/ <\vphantom <1 c>> \right. > c>\). Через узел \(\left(i,n+1\right)\) проведем прямую с наклоном \(k\) (характеристику) и найдем точку ее пересечения с временным слоем \(t_n\) (точка А, рис. 3а). Определим безразмерный параметр \(r=\mathord <\left/ <\vphantom h>> \right. > h>\) — т.н. число Куранта-Фридрихса-Леви. Нетрудно видеть, что при \(0\le r\le 1\) точка А будет находиться между узлами с номерами \(\left(i\right)\) и \(\left(i-1\right)\) на расстоянии \(rh\) от правого узла и \(\left(1-r\right)h\)- от левого.

Рассмотрим простейшую линейную интерполяцию по двум ближайшим точкам. В этом случае

Таким образом, мы пришли к схеме «уголок». Линейная интерполяция привела к схеме первого порядка аппроксимации.

а)	б)
Рис. 3

Для квадратичной интерполяции необходимы три точки. Выберем в качестве таковых узлы с номерами \(i-1,<\rm\; \; >i,<\rm\; \; >i+1\)(рис. 3b) и построим интерполяционный квадратичный полином Лагранжа:

Интерполяционная формула (2.27) эквивалентна разностной схеме Лакса — Вендроффа:

Эту схему часто записывают в т.н. двухэтапной форме. На первом этапе по схеме Лакса вычисляются промежуточные значения \(u_^\)в центрах ячеек:

На втором этапе по схеме «крест» находятся неизвестные значения функции на новом временном слое:

Схема Лакса-Вендроффа имеет второй порядок аппроксимации на решении как по времени, так и по пространству. Анализ других ее свойств будет проведен позднее.

Следует отметить, что все последующие схемы, получаемые квадратичной интерполяцией, будут иметь второй порядок аппроксимации на решении исходного дифференциального уравнения. Это следует из того, что начальные данные, заданные в виде параболы, будут переноситься по характеристикам на новый временной слой точно, без каких либо искажений.

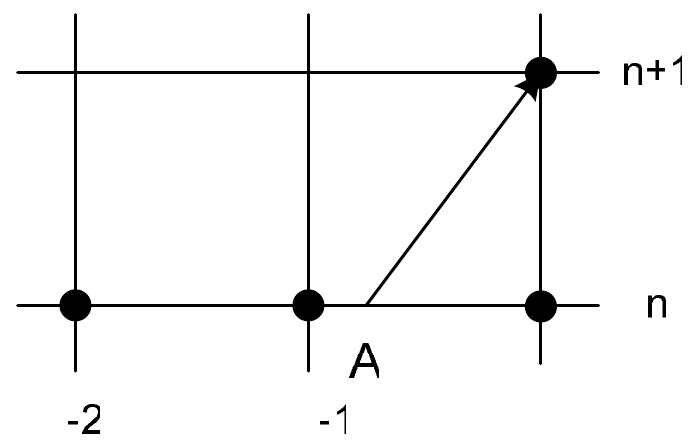
Если использовать для построения квадратичного полинома узлы \(i-2,<\rm\; \; >i-1,<\rm\; \; >i\), (рис. 4а) то квадратичная интерполяция дает:

Подставляя сюда координаты узлов \(x_i = ih\)получаем:

$$\begin \left(A\right)=0.5\cdot r\left(1-r\right);<\rm\; \; \; >P_ \left(A\right)=r\cdot \left(2-r\right);> \\ \left(A\right)=1-r+0.5\cdot r\left(1-r\right)> \end$$

и приходим к разностной схеме Бима-Уорминга

$$\frac^ -u_^ ><<\rm\tau >> +c\cdot \frac<3u_^ -4u_^ +u_^ > =\frac <2>\cdot \frac^ -2u_^ +u_^ > > (2.32)$$

а)	б)
Рис. 4

При увеличении количества используемых узлов на текущем временном слое и повышения порядка полиномов Лагранжа, порядок аппроксимации также будет повышаться.

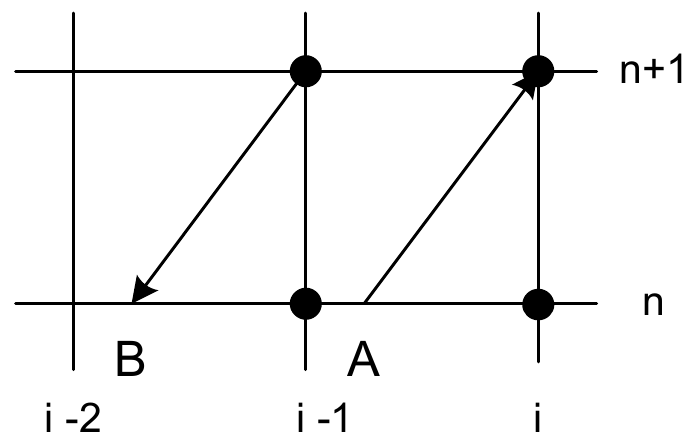
Для включения в описанную схему действий узлов сетки, расположенных на других временных слоях, значения, заданные в этих узлах, сносятся на текущий слой по характеристикам. Проиллюстрируем это на примере шаблона E для схемы Карлсона (рис. 4в). Построим точку B пересечения характеристики из узла \(\left(i-1,n+1\right)\) с текущим временным слоем: \(x_ =\left(i-1\right)h-rh\) и снесем в нее значение сеточной функции из узла \(\left(i-1.n+1\right):u\left(B\right)=u_^\). Интерполяционная формула в этом случае выглядит как:

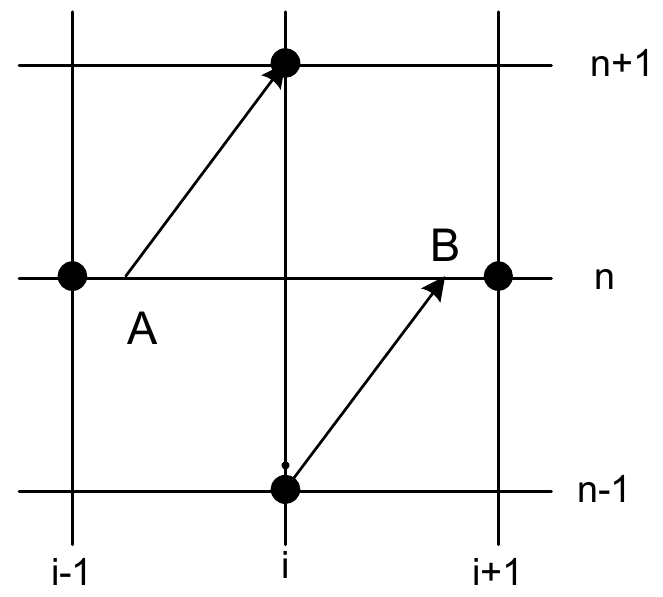
Для трехслойной явной схемы «крест» (рис. 5а) на текущий временной слой сносится значение сеточной функции со слоя \(n — 1\). Проведем характеристику из узла с номером \(\left(i,n-1\right)\), расположенном на слое \(\left(n-1\right)\), до пересечения с текущим слоем в точке B с координатой \(x_ =x_ +hr\). В эту точку переносится значение сеточной функции из узла \(\left(i,n-1\right)\): \(u\left(B\right)=u_^\). Интерполяционный полином строится по токам \(x_ ,<\rm\; >x_ +rh,<\rm\; >x_\):

В результате приходим к выражению:

$$u_^ =u_^ +ru_^ -ru_^ ;<\rm\; \; \; >\Rightarrow <\rm\; \; \; >\frac^ -u_^ ><2<\rm\tau >> <\rm +c>\cdot \frac^ -u_^ > <2h> <\rm =0\; ;>(2.35)$$

а)	б)
Рис. 5

В заключение этого раздела рассмотрим трехслойный вычислительный шаблон (рис. 5в), состоящий из узлов с номерами \(\left(i,n\right);\left(i-1,n\right);\left(i-1,n-1\right);\left(i,n+1\right)\). Интерполяционный многочлен строится по трем узлам \(\left(i,n\right);\left(i-1,n\right);\left(i-1,n-1\right)\)и имеет вид:

В результате приходим к разностной схеме, известной под названиями «КАБАРЕ» и схема Айзерлиса

Линейное уравнение переноса

При классификации уравнений с частными производными (2.1) отмечалось, что уравнения первого порядка называются также уравнениями переноса. Это объясняется тем, что такие уравнения описывают процессы переноса частиц в средах, распространения возмущений и т.п.

В общем случае уравнения переноса могут иметь значительно более сложный вид (например, интегродифференциальное уравнение Больцмана в кинетической теории газов). Однако здесь мы ограничимся линейным уравнением с частными производными первого порядка. Его решение представляет интерес не только с практической точки зрения; в еще большей степени это уравнение полезно при разработке и исследовании разностных схем.

Будем считать, что искомая функция Uзависит от времени tи одной пространственной переменной х. Тогда линейное уравнение переноса может быть записано в виде

(2.23)

Здесь а — скорость переноса, которую будем считать постоянной и положительной. Это соответствует переносу (распространению возмущений) слева направо в положительном направлении оси х. Правая часть F(x, t) характеризует наличие поглощения (или, наоборот, источников) энергии, частиц и т.п. в зависимости от того, какой физический процесс описывается уравнением переноса.

Характеристики уравнения (2.23) определяются соотношениями х — at = С = const. При постоянном а они являются прямыми линиями, которые в данном случае (а > 0) наклонены вправо (рис. 2.5).

Рис. 2.5. Область решения

Расчетная область при решении уравнения (2.23) может быть как бесконечной, так и ограниченной. В первом случае, задавая начальное условие при t = 0:

(2.24)

получаем задачу Коши для полуплоскости На практикеобычно приходится решать уравнение переноса в некоторой ограниченной области (например, в прямоугольнике ; см. рис. 2.5). Начальное условие (2.24) в этом случае задается на отрезке l1; граничное условие нужно задать при х = 0, т.е. на отрезке l2, поскольку при а > 0 возмущения распространяются вправо. Это условие запишем в виде

(2.25)

Таким образом, задача состоит в решении уравнения (2.23) с начальным и граничным условиями (2.24) и (2.25) в ограниченной области G:

Убедиться в том, что данная задача поставлена правильно (корректно) можно, проанализировав решение уравнения (2.23), которое при F(x, t) = 0 имеет вид

(2.26)

где Н — произвольная дифференцируемая функция. В этом легко убедиться, подставляя (2.26) в уравнение (2.23). Решение (2.26) называется бегущей волной (со скоростью а). Это решение постоянно вдоль каждой характеристики: при х — at = С искомая функция U = Н(х — at) = Н(С) постоянна. Таким образом, начальные и граничные условия переносятся вдоль характеристик, поэтому они должны задаваться на отрезках l1и l2 расчетной области G(см. рис. 2.5).

Можно также построить аналитическое решение задачи Коши для неоднородного уравнения (2.23). Заметим лишь, что решение этой задачи меняется вдоль характеристики, а не является постоянным.

Рассмотрим разностные схемы для решения задачи (2.23) — (2.25). Построим в области Gравномерную прямоугольную сетку с помощью прямых xi = ih (i =0,1. I) и . Вместо функций U(x,t), F(x,t), Ф(х) и будем рассматривать сеточные функции, значения которых в узлах (xi, tj) соответственно равны и . Для построения разностной схемы необходимо выбрать шаблон. Примем его в виде правого нижнего уголка(рис. 2.6). При этом входящие в уравнение (2.23) производные аппроксимируются конечно-разностными соотношениями с использованием односторонних разностей:

(2.27)

Рис. 2.6. Правый нижний уголок

Решая это разностное уравнение относительно единственного неизвестного значения на (j + 1)-ом слое, получаем следующую разностную схему:

(2.28)

Полученная схема явная, поскольку значения сеточной функции в каждом узле верхнего слоя выражаются явно с помощью соотношений (2.28) через ранее найденные ее значения на предыдущем слое.

Для начала счета по схеме (2.28), т.е. для вычисления сеточной функции на первом слое, необходимы ее значения на слое j= 0. Они определяются начальным условием (2.24), которое записываем для сеточной функции:

(2.29)

Граничное условие (2.25) также записывается в сеточном виде:

(2.30)

Таким образом, решение исходной дифференциальной задачи (2.23) — (2.25) сводится к решению разностной задачи (2.28) – (2.30). Найденные значения сеточной функции принимаются в качестве значений искомой функции и в узлах сетки.

Алгоритм решения исходной задачи (2.23) — (2.25) с применением рассмотренной разностной схемы достаточно прост. На рис. 2.7 представлена его структурограмма. В соответствии с этим алгоритмом в памяти компьютера хранится весь двумерный массив , и он целиком выводится на печать по окончании счета. С целью экономии памяти (и если эти результаты не понадобятся для дальнейшей обработки) можно воспользоваться тем, что схема двухслойная, и хранить лишь значения сеточной функции на двух соседних слоях . Рекомендуем читателю соответственным образом модифицировать представленный алгоритм и построить новую структурограмму.

Рис. 2.7. Алгоритм решения линейного уравнения переноса

Укажем теперь некоторые свойства данной разностной схемы. Она аппроксимирует исходную задачу с первым порядком, т.е. невязка имеет порядок O(h+τ). Схема условно устойчива; условие устойчивости имеет вид

(2.31)

Эти свойства схемы установлены в предположении, что решение U(x, t), начальное и граничное значения Ф(х) и дважды непрерывно дифференцируемы, а правая часть F(x, t) имеет непрерывные первые производные.

Поскольку схема (2.28) устойчива и аппроксимирует исходную задачу, то в соответствии с приведенной в разд. 2.1 теоремой сеточное решение сходится к точному с первым порядком при . Отметим, что при а 0 эта схема не сходится.

Граничное условие для уравнения переноса (2.23) при а 0). Такая аппроксимация называется противопотоковой и широко используется при численном решении уравнений переноса.

При построении явной разностной схемы (2.28) производная ¶U/¶х аппроксимировалась с помощью значений сеточной функции на j-ом слое; в результате получилось разностное уравнение (2.27), в котором использовано значение сеточной функции лишь в одном узле верхнего слоя. Если производную¶U/¶х аппроксимировать на (j + 1)-ом слое (шаблон изображен на рис. 2.9), то получится неявная схема. Разностное уравнение примет вид

(2.34)

Рис. 2.9. Правый верхний уголок

Разрешая это уравнение относительно , приходим к следующей разностной схеме:

(2.35)

Это двухслойная трехточечная схема первого порядка точности. Она безусловно устойчива (при а > 0). Хотя формально данная разностная схема строилась как неявная, практическая организация счета по ней проводится так же, как и для явных схем.

Действительно, в правую часть уравнения (2.35) входит значение на (j+1)-ом слое, которое при вычислении уже найдено. При расчете значение берется из граничного условия (2.30). По объему вычислений и логике программы (см. рис. 2.7) схема (2.35) аналогична схеме (2.28), однако безусловная устойчивость делает ее более удобной, поскольку исключается ограничение на величину шага.

Схему (2.28) можно применять для решения задачи Коши в неограниченной области, поскольку граничное условие (2.30) в этой схеме можно не использовать.

Рис. 2.10. Прямоугольник

Рассмотрим еще одну разностную схему, которую построим на симметричном прямоугольном шаблоне (рис. 2.10). Производная по tздесь аппроксимируется в виде полусуммы отношений односторонних конечных разностей в (i — 1)-м и i-м узлах, а производная по x — в виде полусуммы конечно-разностных соотношений на j—ми (j + 1)-ом слоях. Правую часть вычисляют в центре ячейки, хотя возможны и другие способы ее вычисления (например, в виде некоторой комбинации ее значений в узлах). В результате указанных аппроксимаций получим разностное уравнение в виде

(2.36)

Данная двухслойная четырехточечная схема также формально построена как неявная. Однако из (2.36) можно выразить неизвестное значение через остальные, которые предполагаются известными:

(2.37)

Построенная схема имеет второй порядок точности. Она устойчива на достаточно гладких решениях.

Схема (2.37) получена для случая а > 0. Аналогичную ей схему при а 0, а2 > 0 — скорости переноса вдоль осей х, у, (2.39) — начальное условие при t= 0; (2.40) — граничные условия при х =0, y= 0.

В трехмерной области (х, у, t) построим разностную сетку, ячейки которой имеют форму прямоугольного параллелепипеда. Для этого проведем координатные плоскости через точки деления осей х, у, t:

Значение сеточной функции в узле (i, j, k), с помощью которой аппроксимируются значения , обозначим через . Построим безусловно устойчивую разностную схему первого порядка точности, аналогичную схеме (2.35). Шаблон изображен на рис. 2.11, где выделена одна ячейка разностной сетки. Сплошными линиями соединены узлы шаблона. Нижний слой (нижнее основание параллелепипеда) имеет номер k, верхний k+ 1.

Рис. 2.11. Шаблон для двумерного уравнения

По аналогии с (2.34) запишем разностное уравнение, аппроксимирующее дифференциальное уравнение (2.38):

Разрешим это уравнение относительно значения сеточной функции в узле :

(2.41)

Вычислительный алгоритм этой схемы аналогичен алгоритму одномерной схемы (2.35). Здесь также счет производится по слоям k= 1,2. К. При k= 0 используется начальное условие (2.39), которое нужно переписать в разностном виде:

(2.42)

На каждом слое последовательно вычисляют значения сеточной функции в узлах. При этом последовательность перехода от узла к узлу может быть различной: двигаются параллельно либо оси х, либо оси у. Во втором случае последовательность вычисляемых значений следующая:

На рис. 2.12 показана нумерация узлов, соответствующая данной последовательности вычислений на каждом временном слое. Точками отмечены расчетные узлы сетки, крестиками — граничные узлы, в которых значения сеточной функции задаются граничными условиями (2.40). Эти условия обходимо записать в сеточном виде:

. (2.43)

Рис. 2.12. Последовательность вычислений

При этом значения в угловой точке (х = 0, у = 0) в данной разностной схеме не используются.

Алгоритм решения смешанной задачи (2.38 – 2.40) для двумерного уравнения переноса по схеме (2.41) с учетом сеточных начального и граничных условий (2.42) и (2.43) представлен на рис. 2.13. При этом некоторые блоки (вычисление начальных значений uij, значений на границе пересылка ) даны схематически, хотя каждый из них представляет циклический алгоритм.

Рис. 2.13. Алгоритм решения двумерного уравнения переноса

В данном алгоритме предусмотрено хранение в памяти машины не полного трехмерного массива искомых значений , а лишь значений на двух слоях: — нижний слой, — верхний слой (искомые значения). Введен счетчик выдачи l, решение выдается через каждые Lслоев; при L = 1 происходит выдача результатов на каждом слое. Блок «Вычисление » вычисляет искомое значение по формуле, которая в принятых в структурограмме обозначениях имеет вид

Схема лакса для уравнения переноса

Рассмотрим уравнение, которое описывает локальные изменения некоторой скалярной величины (это может быть, например, температура или концентрация растворенных и/или взвешенных веществ), обусловленные только переносом (адвекцией) по заданным траекториям:

где U, V, W представляют собой компоненты скорости вдоль трехмерной декартовой системы координат. Это уравнение имеет важное самостоятельное значение, поскольку необходимость в его решении появляется на одном из этапов метода расщепления по физическим процессам. Качество общего решения задачи адвекции — диффузии — реакции сильно зависит от того, каким образом аппроксимированы члены, описывающие адвективный перенос. Ошибки аппроксимации, проявляющиеся в виде паразитной дисперсии и аппроксимационной вязкости, приводят не только к количественному, но и к качественному искажению получаемого решения. Ввиду большой практической значимости, проблема поиска новых направлений кардинального улучшения диссипативных и дисперсионных свойств численных схем для уравнения переноса является чрезвычайно актуальной, а соответствующая задача может быть отнесена к разряду фундаментальных задач вычислительной гидродинамики. Именно важностью приложений объясняется большое внимание исследователей к решению подобного рода уравнений. В последние годы интенсивное изучение проблем механики сплошной среды, прогноза погоды, распространения загрязняющий веществ, динамики океана привело к разработке достаточно универсальных и эффективных методов численного уравнения адвекции (Вабищевич и др., 2000; Марчук, 1974; Марчук, 1982; Рождественский, Яненко, 1978; Роуч, 1980; Самарский, Вабищевич, 1998; Arakawa, 1997; Bryan, 1997). Наряду с этим продолжается и поиск принципиально новых подходов к решению этой задачи (Головизнин, Карабасов, 1998; Головизнин, Самарский, 1998; Головизнин, Самарский, 1998). В данном разделе мы рассмотрим некоторые из таких подходов.

Рассмотрим сначала простейший, одномерный, вариант уравнения переноса субстанций вдоль траекторий с постоянной скоростью :

где — начальное распределение при . Скорость адвекции U можно рассматривать как фазовую скорость перемещения возмущения вдоль оси , которое в начальный момент времени представляет собой волну:

где — амплитуда в начальный момент времени, — волновое число, L — длина волны, — мнимая единица. Найдем решение уравнения (82) методом разделения переменных. Представим в виде произведения некоторых двух функций:

После подстановки выражения (84) в уравнение (82) и деления результата на получим

Выполнив интегрирование, получим:

или , , где , — постоянные интегрирования. Следовательно, , . Искомая функция —

Используя начальное условие (83), имеем: , , а следовательно, окончательное решение можно представить в следующем виде:

при условии, что — есть дифференцируемая функция. Это решение описывает процесс начального возмущения вдоль характеристики . Это означает, что на любой прямой . Итак, задача (82) при определяет процесс распространения возмущения в сторону возрастающих значений . Это, хорошо известное положение учитывается и при конструировании разностных схем для уравнения адвекции. Среди наиболее употребительных на практике схем для численного решения одномерного уравнения переноса можно отметить следующие схемы (Белов и др., 1989; Мезингер, Аракава, 1979; Роуч, 1980):

·согласованную, трехуровневую по времени, условно устойчивую схему центральных разностей второго порядка точности. Условие устойчивости для данной схемы соответствует критерию Куранта — Фридрихса — Леви (КФЛ): ;

·согласованную неявную схему направленных разностей первого порядка точности. Эта схема абсолютно устойчива и диссипативна, но ей свойственна вычислительная вязкость;

·неявную двухуровенную схему трапеций второго порядка (схема Кранка-Николсона). Эта схема нейтральна и абсолютно устойчива при любых шагах по пространству и времени. Кроме того она свободна от эффекта вычислительной вязкости;

·согласованную двухтактную схему Мацуно (Эйлера с пересчетом), первого порядка точности по времени и второго — по пространству. Эта схема устойчива при выполнении критерия КФЛ. Ей свойственна вычислительная вязкость, причем вязкость максимально воздействует на волны длиной . На волны длиной счетная вязкость не влияет;

·согласованную явную схему четвертого порядка точности по пространству и второго — по времени. Схема условно устойчивая, причем условие устойчивости оказывается более жестким, чем для схем первого и второго порядка по пространству. Для схем четвертого порядка по пространству шаг по времени должен быть примерно на 27% меньше, чем для схем второго порядка (при одних и тех же U и ). В случае применения этой схемы эффект вычислительной вязкости не проявляется;

·явную согласованную схему Лакса-Вендрофа второго порядка точности. Важным достоинством схемы является ее способность подавлять волны длиной , которые нельзя правильно представить на сетке. Тем самым появляется возможность демпфирования коротких волн в процессе численного интегрирования уравнений. Схема условно устойчива. Условие устойчивости соответствует критерию КФЛ. При схема Лакса-Вендрофа диссипативна. По мере увеличения длин волн диссипативность схемы уменьшается.

В работах (Головизнин, Карабасов, 1998; Головизнин, Самарский, 1998; Головизнин, Самарский, 1998) предложена принципиально новая базисная линейная разностная схема для одномерного модельного уравнения конвективного переноса с постоянной скоростью, названная схемой «кабаре». Эта схема имеет ряд уникальных особенностей, в связи с чем ее дальнейшее изучение представляет как теоретический, так и прикладной интерес. Главной особенностью схемы «кабаре» является то, что она оказывается точной при двух различных числах Куранта, лежащих в области ее устойчивости. Это означает, что в этих случаях данная схема не содержит также и аппроксимационной дисперсии, что обеспечивает наличие у нее достаточно хороших транспортных свойств. Так, на нерегулярной расчетной сетке схема без существенного искажения переносит нетривиальные начальные распределения на расстояния, на порядок больше, чем это позволяют классические линейные схемы, такие, например, как схема Лакса-Вендрофа. Другая особенность схемы заключается в том, что она имеет второй порядок аппроксимации на нерегулярных расчетных сетках и исключает распространение возмущений вверх по потоку. Кроме того, схема «кабаре» является консервативной (дивергентной), и для нее автоматически выполняется закон сохранения квадрата переносимой функции, который является аналогом закона сохранения энергии. Поэтому можно говорить о том, что эта схема обладает свойством полной консервативности. Путем тестовых расчетов было показано, что при наличии значительных пространственных вариаций у переносимого профиля решение теряет свою монотонность. Поэтому в схему «кабаре», как и в другие малодиссипативные линейные схемы, необходимо включать алгоритмы нелинейной коррекции, монотонизирующие получаемые решения (Головизнин, Карабасов, 1998). Есть все основания полагать, что распространение данной схемы на многомерный случай может также привести к получению качественно новых результатов.

Если скорость — переменная по пространству и во времени, то нахождение задачи (82) в аналитическом виде, в общем случае, невозможно. Именно в таких ситуациях и оказывается необходимым применение численных методов, основанных на разностных аппроксимациях. Следует только иметь виду, что даже при использовании неявных диссипативных разностных схем возможно нарушение счетной устойчивости (Белов и др., 1989). Особенно это проявляется в нелинейных задачах. Это объясняется следующим (Мезингер, Аракава, 1979). Если разложить решение разностной задачи и коэффициент в ряд Фурье, то произведения рядов Фурье приведут к гармоникам как более длинным, чем взаимодействующие, так и более коротким. В результате такого процесса в ряде случаев может произойти перекачка «энергии» от ошибок округления из длинных волн в более короткие, и процесс вычислений окажется неустойчивым, даже несмотря на то, что данная разностная схема с постоянным коэффициентом будет счетно устойчивой. Она также иногда появляется и при решении линейных задач с переменными коэффициентами. Поэтому построение разностных схем для нелинейных уравнений с переменными коэффициентами, устойчивых в отношении к любым возмущениям, является чрезвычайно актуальной задачей. В большинстве случаев подавление счетной неустойчивости возможно с помощью диссипативных разностных схем, отвечающих определенному выбору коэффициента счетной вязкости. Однако такие схемы, как правило, оказываются схемами первого порядка аппроксимации либо по , либо по , либо и по , и по .

Рассмотрим теперь задачу адвекции на плоскости :

Здесь , . Будем предполагать, что компоненты вектора скорости U, V в каждый момент времени удовлетворяют уравнению неразрывности

Пусть область представляет собой прямоугольник и решение задачи (86) вместе с коэффициентами U и V является периодическим, то есть принимает на границах прямоугольника одинаковые значения. Используя оператор конвективного переноса в недивергентной форме , задачу (86) — (87) можно записать в операторной форме:

Покажем, что в исследуемой задаче оператор удовлетворяет условию . Действительно, рассматривая гильбертово пространство со скалярным произведением, запишем

Преобразуем подынтегральное выражение, используя для этого уравнение неразрывности (89). Получим: . Поэтому . Отсюда, с помощью условия периодичности решения на границах расчетной области, получаем доказательство условия . Из этого вытекает важный вывод о том, что оператор является кососимметрическим и, следовательно, допускает конструирование абсолютно устойчивых разностных схем.

Попытаемся теперь оператор расщепить таким образом, чтобы каждый из элементарных операторов также удовлетворял условию

В этом случае разностная схема покомпонентного расщепления позволит получить абсолютно устойчивую разностную схему второго порядка точности. Важно заметить, что формальное разложение оператора на составные части

не удовлетворяет условию (93). В этом случае мы получаем следующие соотношения:

Таким образом, операторы в форме (94) не могут быть взяты в качестве элементарных для построения схемы последовательного расщепления.

Выберем теперь более сложную форму представления операторов :

Каждый из таких операторов теперь удовлетворяет условию (93), а сумма этих операторов в точности равна . В самом деле, составим сумму

Здесь мы воспользовались уравнением неразрывности (89).

Таким образом, все необходимые условия для применимости метода расщепления соблюдены и можно записать, например, схему двуциклического покомпонентногорасщепления на временном интервале для случая оператора :

Как было отмечено выше, если , то при достаточной гладкости решения задачи и элементов матриц система разностных уравнений (96) абсолютно устойчива и эта схема аппроксимирует исходную задачу со вторым порядком точности по . Кроме того, данный прием снимает весьма сильное требование коммутативности операторов. Это — важный и поучительный пример того, насколько существенно учитывать математические особенности решаемой задачи и сущность описываемых процессов. Формальное, прямолинейное применение методов расщепления может скомпрометировать саму идею.

Выписывая схему (96) мы еще ничего не сказали о путях рациональной аппроксимации оператора конвективного переноса по пространственным переменным . Удобным методом аппроксимации с сохранением аддитивных свойств оператора и его основных качественных особенностей является метод покоординатной аппроксимации (Марчук, 1980). Предположим, что поле скоростей достаточно гладкое и рассмотрим уравнение адвекции в дивергентной (консервативной) форме:

За основу построения разностной схемы возьмем оператор конвективного переноса С, который определяется выражением

а разностный аналог этого соотношения рассмотрим в виде

Разностное выражение (101) аппроксимирует исходный оператор (100) со вторым порядком относительно пространственных шагов и сетки при достаточной гладкости решения и поля скоростей . Однако выражение (101) имеет существенный недостаток, поскольку в такой форме оператор нарушает свою кососимметрическую структуру, то есть теперь . А это означает, что внешне привычная аппроксимация оказывается неудовлетворительной для построения вычислительного алгоритма решения поставленной задачи. Для того, чтобы соотношение выполнялось, необходимо осуществить аппроксимацию оператора (100) в следующем виде (Марчук, Саркисян, 1988):

где , , , . Выражение (102), так же как и (101), аппроксимирует исходный оператор (100) со вторым порядком относительно пространственных шагов сетки и . Таким образом построенный оператор сохраняет важное свойство кососимметричности и, более того, каждый из операторов и , определяемых выражениями

также удовлетворяет условиям , (Марчук, Саркисян, 1988).

Итак, необходимые пространственные аппроксимации оператора конвективного переноса проведены. Теперь задача состоит в решении системы обыкновенных дифференциальных уравнений

где , — вектор-функция времени t с компонентами , а каждый из операторов и удовлетворяет условиям , . Это значит, что данная задача может быть решена с помощью метода расщепления. Например, схема (96) двуциклического покомпонентногорасщепления на временном интервале для оператора будет иметь теперь следующий вид:

Таким образом, исходная задача (86) — (88) редуцировалась к системе простейших одномерных разностных уравнений, решение каждой их которых возможно с помощью метода факторизации трехточечных разностных уравнений (метода прогонки). Совершенно аналогично решается уравнение адвекции в трехмерном пространстве, когда оператор конвективного переноса расщепляется на три кососимметричных оператора.

Рассмотрим теперь другой вариант построения конечно-разностной схемы для двумерного уравнения адвекции (86) — (88) на интервале времени, равном шагу по времени от до — схему предиктор-корректор (Белов и др., 1989; Моделирование процессов переноса и трансформации вещества в море, 1979). Здесь уравнение (86) расщепляют на два уравнения так, чтобы в каждом из них присутствовали производные только по одной пространственной переменной:

Каждое из уравнений системы (107) решается на первой половине шага по времени, то есть на интервале от до , который разбивается на две части (дробных шага), с помощью следующих неявных двухточечных схем направленных разностей против потока:

Эти конечно-разностные схемы применяются последовательно так, что решение, полученное на предыдущем дробном шаге, используется в качестве начального условия для следующего дробного шага. В совокупности схемы (108), (109) обеспечивают получение решения на момент времени . Поскольку в этих схемах применяются направленные разности по времени и по пространству, то аппроксимация ими уравнения (86) имеет первый порядок точности. Схемы (108), (109) называются схемами предиктора.

Далее, на интервале времени от до , уравнение (86) решается с помощью схемы центральных разностей

которая аппроксимирует уравнение (86) уже со вторым порядком точности. Эта схема называется схемой корректора.

Рассмотрим более подробно решение системы уравнений (107). Поскольку оба уравнения этой системы однотипны, рассмотрим решение только первого уравнения

Для простоты разобьем шаг по времени на два равных интервала: от до и от до . На первом интервале (дробном шаге) от до используется схема предиктора

Двухточечные схемы (112) формально можно записать в виде единой трехточечной схемы, объединяющей случаи и :

где , , , . Схема (113), записанная для точек i = 1, 2, . I-1, представляет собой систему алгебраических уравнений, в которых содержатся неизвестные функции в трех соседних точках: , , . Матрица коэффициентов этой системы уравнений — трехдиагональная. В точках i = 0, i = I ставятся соответствующие задаче граничные условия (например, , ). Система уравнений (113) с граничными условиями является замкнутой. Для решения этой системы применяется метод разностной факторизации (прогонки). Запишем систему (113) в следующем виде:

Для того, чтобы обеспечить точное соблюдение граничных условий, полагаем , , , , , . Выразим из первого уравнения . Получим:

где , . Подставляя (115) во второе уравнение, найдем :

где , . Повторяя далее процесс подстановки, для некоторого промежуточного значения i получим:

где , . Для i = I-1 из (117) получим :

где , . Наконец, подставляя (118) в последнее уравнение системы (114), получаем:

Поскольку , , , то из (119) следует, что граничное условие при в точности выполняется. Таким образом, видно, что метод прогонки реализуется с помощью двух циклов вычислений, которые называются прогонками вперед и назад. На прогонке вперед (индекс i возрастает, пробегая значения i = 1, 2, . I-1) рассчитываются вспомогательные величины , , , . На прогонке назад (индекс i убывает, пробегая значения i = I-1, I-2, . 1) по формуле определяются искомые величины, причем .

Нетрудно убедиться в том, что граничные условия в точках , будут использоваться только тогда, когда поток направлен внутрь области определения решений. В противных случаях граничные условия не используются. Так, например, для водоемов на твердых границах, в створах вытекающих рек и на открытой границе обычно задается условие равенства нулю производной по направлению внешней нормали n к границе: .

Метод прогонки устойчив, если . Очевидно, что в данном случае это условие выполняется, поскольку , а .

Покажем, что аппроксимация уравнения (111) конечно-разностным уравнением (112) приводит к появлению эффекта счетной вязкости (Белов и др., 1989). Для этого разложим решение уравнения (111) в ряды Тейлора в окрестности точки , , :

Подставляя данные разложения в конечно-разностное уравнение (113), получаем:

где — коэффициент искусственной или «счетной» вязкости. При получении уравнения (120) предполагалось, что отброшенные члены в разложениях малы.

При определенных условиях (больших скоростях течения и/или шагах разностной сетки) эффект схемной вязкости значительно возрастает, что, естественно, приводит к существенному сглаживанию полей температуры или переносимой субстанции. Именно поэтому для уточнения решения и используется схема корректора второго порядка точности с центральными разностями, применение которой не приводит к появлению эффекта счетной вязкости. Схема корректора для уравнения (111) записывается в следующем виде:

Таким образом, применение схем предиктора и корректора обеспечивает получение решения в момент времени . Аппроксимация уравнения (111) схемами предиктора и корректора имеет второй порядок точности.

Покажем теперь, что комбинация схем (113) и (121) оказывается устойчивой. Воспользуемся для этого методом Неймана. Предположим, что . Пусть для определенности . В этом случае из (112) получаем:

Из конечно-разностных схем (121) и (122) исключим неизвестную величину с дробным временным индексом . Для этого запишем схему (122) для точек и :

Вычитая из первого соотношения второе, получим:

Схему (121) запишем для точки : . Отсюда находим

Используя выражение (124), уравнение (123) можно представить в следующем виде:

Подставим теперь в (125) волновое решение вида , где — амплитуда, — мнимая единица. После сокращения на общий сомножитель получаем следующее выражение для множителя перехода:

где . Как отмечалось выше, эта величина связывает амплитуды возмущений на соседних уровнях по времени. Поскольку модули комплексных чисел в числителе и знаменателе равны, то , а это и означает, что рассмотренная схема предиктор-корректор устойчива.

Для приближенного решения начально-краевых задач для уравнения переноса широко используются также разностные схемы, для которых выполнен принцип максимума — монотонные разностные схемы. Для уравнений переноса легко строятся безусловно монотонные разностные схемы первого порядка по пространству с использованием направленных разностных производных (Самарский, 1983). Хорошо известно (Годунов, 1959), что в классе однородных линейных схем отсутствуют схемы с порядком аппроксимации, по пространству выше первого. При численном решении задач механики сплошной среды строятся различные классы нелинейных монотонных схем, которые в основной части расчетной области имеют повышенный порядок — второй и выше. В настоящее время большое внимание в прикладных исследованиях по механике сплошной среды уделяется разностных схемам типа TVD( T otal V ariation D iminishing). Безусловная монотонность в этих и им подобных схемах достигается за счет нелинейного ограничения потоков в исходной схеме с направленными разностями второго порядка. Эти исследования были инициированы в работах (Колган, 1972; Harten, 1983) и продолжены во многих других (Hartenetal., 1986; Harten, Osher,1987; Hartenetal., 1987). В работе (Самарский, Вабищевич, 1998) отмечается возможность построения монотонных однородных нелинейных разностных схем для уравнения переноса на основе регуляризации (возмущения) схемы второго порядка аппроксимации. В качестве производящей схемы выбираются схемы со стандартными аппроксимациями первой производной второго порядка — центральными разностями и направленными разностями второго порядка, а также их комбинациями.

Для того, чтобы пояснить основную идею построения такого рода схем, в прямоугольной области рассмотрим, следуя работе (Вабищевич и др., 2000), нестационарное уравнение переноса с конвективными слагаемыми в недивергентной (характеристической) форме:

Уравнение (126) дополняется начальным условием

Граничные условия задаются на той части границы, на которой поток входит в область. Для простоты ограничимся случаем

где — нормаль к границе расчетной области. При ограничениях (128) нет необходимости формулировать какие-либо граничные условия для однозначного определения решения задачи (126), (127). Для поставленной задачи справедлив принцип максимума: , если . Кроме того, верна априорная оценка в : , где . Естественно ориентироваться на построение таких разностных схем, для которых эти важнейшие свойства были бы выполнены.

Рассмотрим теперь разностную схему с направленными разностями. После дискретизации по пространственным переменным от (126) придем к дифференциально-операторному уравнению

В соответствии с (127) положим

При решении задач для уравнений переноса обычно ориентируются на использование явных схем. Простейшей является двухслойная явная схема, когда дифференциально-разностной задаче (129), (130) ставится в соответствие разностное уравнение

При построении схем с направленными разностями учитывается знак скорости в соответствующем направлении. Будем использовать следующие обозначения:

С учетом (128) положим ,

Разностная схема (131), (132) устойчива в при следующих ограничениях (условие Куранта) на шаг по времени:

При этом для решения имеет место оценка , где . Разностная схема (131) с центрально-разностными аппроксимациями конвективных слагаемых

является безусловно неустойчивой и немонотонной при всех . Но ее потенциальное преимущество перед схемой с направленными разностями (131), (132) связано со вторым порядком аппроксимации по пространству.

Помимо аппроксимаций (134), для конвективных слагаемых можно использовать направленные разности второго порядка аппроксимации. Не обсуждая проблемы, связанные с аппроксимациями в приграничных узлах, полагаем

Комбинируя центрально-разностные аппроксимации, можно определить разностный оператор конвективного переноса в следующем параметрическом виде:

В этом случае значение соответствует использованию центрально-разностных аппроксимаций (134), — аппроксимаций направленными разностями второго порядка. Среди аппроксимаций второго порядка (136) отдельного упоминания заслуживает случай и — аппроксимации третьего порядка.

Монотонные разностные схемы строятся на основе общего методологического принципа получения разностных схем заданного качества — принципа регуляризации разностных схем (Самарский, 1967). При построении монотонных разностных схем проводится нелинейное возмущение коэффициентов разностной схемы. По существу, речь идет об использовании в отдельных подобластях (вне экстремумов решения) схем второго порядка аппроксимации. Это достигается комбинированием монотонных аппроксимаций первого порядка с немонотонными аппроксимациями более высокого порядка. При построении нелинейных монотонных схем обычно привлекаются соображения физического плана и оперируют, например, потоками, их направлениями и т. д. Фактически речь идет о том, как от одной схемы в части расчетной области перейти к другой схеме в другой части расчетной области, то есть об интерполяции между двумя схемами. Уже имеющиеся работы в этом направлении говорят о том, что можно построить множество таких интерполяционных схем.

В нелинейной регуляризованной схеме используются аппроксимации конвективного переноса, которые имеют форму аппроксимации направленными разностями со специальными регуляризующими множителями:

Принимая во внимание (136), для регуляризующих множителей в работе (Вабищевич и др., 2000) получено следующее представление

Здесь и этот коэффициент выступает в качестве параметра регуляризации. В предельном случае мы приходим к нелинейной аппроксимации (136) второго или третьего (при ) порядка. Монотонность схемы (131), (137), (138.1) — (138.2) (неотрицательность регуляризующих коэффициентов ) обеспечивается выбором коэффициента . Принимая во внимание то, что для , приходим к следующим ограничениям на временной шаг: , где (см. (133)) — минимальный шаг для схемы с направленными разностями первого порядка. Тем самым при минимально допустимом значении параметра предельный шаг по времени в нелинейной монотонной схеме в два раза меньше по сравнению с обычной схемой (131), (132). Отметим, что нет простых соображений в пользу того или иного однозначного выбора параметра . На тестовых расчетах для одномерной задачи показано, что параметр влияет на перемещение профиля с большей или меньшей скоростью по сравнению с точным решением тестовой задачи. Поэтому его связывают с дисперсионными характеристиками разностной схемы. Установлено, что наиболее оптимальным является значение . Важным достоинством рассматриваемых схем является их простота и прозрачность базовых математических конструкций.