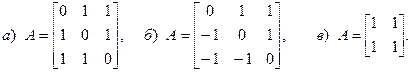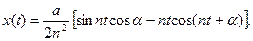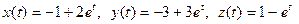МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Дата добавления: 2015-06-12 ; просмотров: 8117 ; Нарушение авторских прав
Цель работы: освоение методики моделирования линейных дифференциальных уравнений в системе MATLAB и SIMULINK.
I. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1. Линейное дифференциальное уравнение.
Многие физические процессы, такие как колебания маятника, движение стрелки гальванометра, изменение высоты при посадке самолета, процессы в электрическом колебательном контуре могут быть описаны линейным однородным дифференциальным уравнением второго порядка
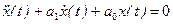
Здесь а0, а1 – постоянные коэффициенты, определяющие характер процесса, точкой обозначается производная по времени. Амплитуда переменной x(t) зависит от начальных условий, например, от начального отклонения x0 маятника и его начальной скорости 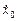
Вид теоретического решения дифференциального уравнения (1) определяется корнями его характеристического полинома
Если корни вещественные и различные р1 = a1`, р2 = a2`, то решение имеет вид
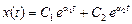
Если корни комплексные р1,2 =a ± ib , то решение имеет вид
Постоянные С1 и С2 находят, подставляя начальные условия в выражения для x(t) и 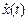
Пример 1. Дано дифференциальное уравнение
Его характеристическое уравнение p 2 + 2p + 2 = 0 имеет корни 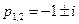
Дифференцируя, находим выражение для 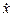
При t = 0 с учетом начальных условий получаем C1 = 2, С2 = 1. Следовательно,
Эффективным средством решения дифференциальных уравнений является численное моделирование в одном из математических пакетов (MATHCAD, MATLAB, SIMULINK и др.). График решения x(t) наблюдается на экране дисплея. В пакете MATLAB для этой цели имеются команды initial, lsim, ode23, ode45, dsolve. Дополнительныe возможности для пользователя предоставляет моделирование в SIMULINK.
1.2. Структурное моделирование линейных дифференциальных уравнений.
При структурном моделировании дифференциальных уравнений в пакете SIMULINK необходимо составить схему моделирования. На ней изображаются вычислительные блоки (усилители, сумматоры, интеграторы) и связи между ними. При проведении моделирования эта схема набирается на экране дисплея с помощью мыши или клавиатуры. По своему смыслу этот процесс аналогичен вводу программы, однако он более прост и нагляден. Подробная информация о реализации таких схем в SIMULINK имеется в разделе 3 учебного пособия Мироновского Л.А., Петровой К.Ю. «Введение в MATLAB» (ГУАП, 2006).
Рассмотрим методику составления схемы моделирования на примере однородного линейного дифференциального уравнения второго порядка
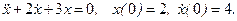
Для построения схемы моделирования воспользуемся методом понижения производной (методом Кельвина). В нем можно выделить четыре шага.
Шаг 1. Разрешаем исходное уравнение относительно старшей производной. В частности для уравнения (2) получаем 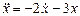
Шаг 2. Полагаем старшую производную известной и выполняем ее последовательное интегрирование, получая все низшие производные и саму переменную х. В случае уравнения (2) для этого потребуется два последовательно включенных интегратора, на выходах которых получим сигналы 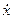
Шаг 3. Формируем старшую производную, используя уравнение, полученное на первом шаге. В нашем примере для этого потребуется сумматор, складывающий сигналы 
Шаг 4. Объединяем схемы, полученные на втором и третьем шагах, в общую схему моделирования, указываем начальные условия интеграторов.
Применение этой методики для уравнения (2) приводит к схеме, показанной на рис. 1. Она содержит два интегратора, два масштабных усилителя и сумматор (обозначен кружочком).
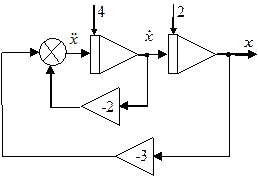 Рис. 1. Схема моделирования уравнения (2) Рис. 1. Схема моделирования уравнения (2) |
Выходной сигнал схемы подается на имитатор осциллографа (блок Scope) или передается в рабочее пространство MATLAB (блоки OUT или ToWorkspase).
1.3. Системы линейных дифференциальных уравнений первого порядка.
Многие технические объекты можно описать системой n линейных дифференциальных уравнений первого порядка:
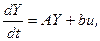
где и – входной сигнал; Y – вектор-столбец выходных переменных yi; b – вектор-столбец коэффициентов bi; A – квадратная матрица коэффициентов aij, 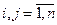
Например, при моделировании летательного аппарата составляющими вектора Y могут быть текущие координаты самолета и скорости их изменения, тогда матрица A будет характеризовать динамику самолета, а слагаемое bи описывать управляющие воздействия, формируемые летчиком или автопилотом.
Один из методов решения системы дифференциальных уравнений основан на предварительном переходе от системы (3) к одному уравнению n-го порядка. Для этого из уравнений системы и из уравнений, полученных их дифференцированием, исключают все переменные кроме одной. Для нее получают одно дифференциальное уравнение. Решая его, определяют эту переменную, а остальные находят, по возможности, без интегрирования.
Пример 2. Дана система из двух дифференциальных уравнений
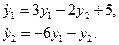
После дифференцирования первого уравнения получаем:
Чтобы исключить у2, вычтем отсюда удвоенное первое уравнение системы (4):
Мы получили линейное неоднородное дифференциальное уравнение второго порядка. Общее решение этого уравнения представляет собой сумму общего решения соответствующего однородного уравнения и частного решения 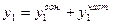
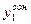
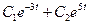
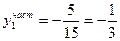
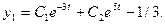
Для определения постоянных коэффициентов С1 и С2 используют начальные условия системы. Аналогичным образом этот метод применяется и для систем уравнений более высоких порядков
1.4. Моделирование системы линейных дифференциальных уравнений.
Если задача описывается системой дифференциальных уравнений первого порядка, то для ее моделирования по методу понижения производной достаточно составить схемы для каждого уравнения отдельно. Например, схема моделирования системы уравнений (4) будет иметь вид, показанный на рис. 2.
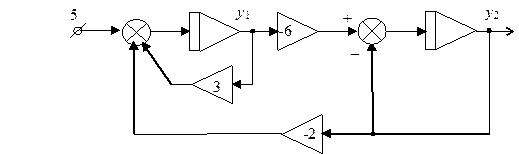 Рис. 2. Схема моделирования системы уравнений (4) Рис. 2. Схема моделирования системы уравнений (4) |
Для наблюдения графиков сигналов у1(t), у2(t) в SIMULINK используется блок осциллографа SCOPE, а для наблюдения фазовой траектории у2 = f (у1) – блок осциллографа XY Graph.
2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
1. Теоретическое решение уравнения (1) при заданных значениях а0, а1 и начальных условиях x(0) = 5, 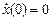
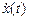
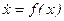
2. Схема моделирования заданного уравнения применительно к SIMULINK.
Теоретическое решение системы дифференциальных уравнений (3) для случая
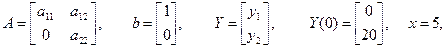
Схема моделирования исходной системы уравнений применительно к SIMULINK.
3. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
- Набрать в SIMULINK схему моделирования уравнения (1), установить коэффициенты и начальные условия.
- Получить осциллограммы x(t),
и
, сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
- Набрать схему моделирования системы уравнений (3), установить коэффициенты и начальные условия (5).
- Получить осциллограммы у1(t), у2(t) и у2 = f(y1), сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
- Выполнить моделирование системы уравнений (3) в MATLAB, используя команду lsim. Cравнить графики, полученные в MATLAB и SIMULINK.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
- Решить следующие линейные дифференциальные уравнения:
а)
б)
- При каком значении а и при каких начальных условиях решение уравнения
имеет вид:
- В чем заключается метод понижения производной? Пользуясь этим методом, составить схемы моделирования для всех вариантов п.1.
- Используя метод понижения производной, составить схемы моделирования следующих дифференциальных уравнений:
а) 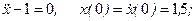
в)
г)
- Схема моделирования представляет собой кольцо из трех интеграторов с единичными коэффициентами и одинаковыми начальными условиями. Найти моделируемое дифференциальное уравнение и его аналитическое решение.
- Как изменятся графики решения линейного однородного дифференциального уравнения при замене знаков всех начальных условий на противоположные?
- Описать процедуру перехода от системы дифференциальных уравнений к одному уравнению и обратную процедуру, рассмотрев случай n=3. Привести пример.
- Составить схему моделирования и найти решение системы линейных дифференциальных уравнений
если матрица A имеет вид
ВАРИАНТЫ ЗАДАНИЙ ПО РАБОТЕ № 2
| № | ||||||||||||
| a1 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,5 | 0,1 | 0,1 | 0,6 |
| a0 | 0,4 | 1,6 | 4,8 | 0,5 | 1,8 | 5,0 | 0,6 | 2,0 | 5,4 | 0,7 | 2,2 | 5,8 |
| a11 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -1,0 | -0,9 | -0,9 | -0,9 | -0,9 | -0,9 |
| a12 | 1,0 | 0,8 | 0,7 | 0,6 | 0,57 | 0,4 | 0.35 | 1,0 | 0,8 | 0,7 | 0,6 | 0,5 |
| a22 | -2,0 | -1,8 | -1,7 | -1,6 | -1,5 | -1,4 | -1,3 | -1,9 | -1,7 | -1,6 | -1,5 | -1,4 |
| № | ||||||||||||
| a1 a0 | 0,1 0,8 | 0,3 2,4 | 6,0 | 0,9 8,8 | 0,1 0,9 | 0,3 2,6 | 0,7 6,4 | 1.1 9,0 | 0,2 1,0 | 0,3 2,8 | 0,8 6,8 | 0,6 5,8 |
| a11 | -0,9 | -0,9 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,8 | -0,5 | -0,5 | -0,5 |
| a12 | 0,4 | 0,3 | 1,0 | 0,8 | 0,7 | 0,6 | 0.5 | 0,4 | 0,3 | 1,0 | 0,8 | 0,7 |
| a22 | -1,3 | -1,6 | -1,6 | -1,6 | -1,5 | -1,4 | -1,3 | -1,2 | -1,1 | -1,5 | -1,3 | -1,2 |
Ответы на контрольный вопрос 1а,б,в,г:
а. 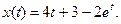
в.
г.
Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ

с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши


по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 







При 

Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема

а на этапе корректора (уточнения) — схема
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 





О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 

С учётом(9) общее решение имеет вид:

Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 
К системе следует добавить начальные условия: 


Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:

Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Модели для решения дифференциальных уравнений
Поскольку моделирование автоматических систем управления чаще всего сводится к решению дифференциальных уравнений, то в первую очередь рассмотрим устройства для их решения, которые в аналоговой вычислительной технике часто называют дифференциальными анализаторами.
В дифференциальных анализаторах реализуются два метода интегрирования дифференциальных уравнений. Один из них основан на повышении порядка производных искомой функции, а другой — на его понижении [29, 61]. Рассмотрим их на примере линейного дифференциального уравнения с постоянными коэффициентами третьего порядка

Для интегрирования дифференциального уравнения методом повышения порядка производных его необходимо решить относительно производной неизвестной функции Z низшего порядка. Приняв Z за производную нулевого порядка, из (14.1) получим

Структурная схема модели для решения уравнения (14.2) показана на рис. 14.1. Из формулы (14.2) следует, что для получения переменной Z необходимы следующие вычислительные блоки: 4-входовой сумматор (блок S на рис. 14.1), три дифференциатора (блоки D) и три умножителя (блоки X) для умножения на коэффициенты AL Выходной сигнал сумматора, обозначенный на схеме рис. 14.1 буквой Z, будет искомым решением уравнения (14.1).
Отметим, что метод повышения порядка производных почти не применяется на практике, так как дифференцирующие блоки весьма чувствительны к помехам (см. гл. 10), которые могут стать источником ошибок. Например, если в электронной вычислительной машине возмущение f(t) подается на суммирующий блок от функ ционального потенциометра, то фактически оно будет изменяться не плавно, а сту-пенчато при переходе подвижного контакта от одного витка потенциометра к другому, что будет регистрироваться дифференцирующими блоками в виде значительных всплесков напряжения. Значительные ошибки в определении мгновенного значения производной имеют место и в точках перехода от одной аппроксимирующей прямой к другой, при вводе возмущения от диодного функционального аппроксиматора и т.п. Метод повышения порядка производных используется только в тех случаях, когда без него нельзя обойтись, например, в специализированных вычислительных машинах. Однако в этом случае используются специальные дифференцирующие устройства, вырабатывающие не мгновенные, а усредненные (сглаженные) значения производных.
Для интегрирования уравнения (14.1) методом понижения порядка производных его нужно решить относительно производной функции Z(t) высшего порядка, т.е.

Структурная схема модели для этого случая показана на рис. 14.2. Из формулы (14.3) видно, что для получения переменной Z необходимы следующие вычислительные блоки: 4-входовой сумматор (блок S на рис. 14.2), три интегратора (блоки I) и три умножителя (блоки X) для введения коэффициентов Bi. Выходной сигнал третьего интегратора, обозначенный на схеме рис. 14.2 буквой Z, будет искомым решением уравнения (14.3).
Достоинством метода понижения порядка, нашедшего наибольшее распространение на практике, является высокая точность, обусловленная применением интеграторов, что устраняет в определенной мере влияние различных флуктуаций, возникающих в схеме.
По конструктивному выполнению моделирующие устройства делятся на матричные и структурные. Устройства матричного типа представляют собой конструктивно законченные наборы из разных вычислительных блоков, каждый из которых позволяет моделировать одно из уравнений системы дифференциальных уравнений.
Такие устройства являются достаточно специализированными и в нашем случае не представляют интереса. Устройства структурного типа реализуют решение дифференциальных уравнений и их систем в том виде, в каком они заданы. Они представляют собой наборы простейших вычислительных блоков, соединяемых между собой определенным образом в зависимости от вида дифференциального уравнения высокого порядка или системы дифференциальных уравнений первого порядка, и уступают матричным только по оперативности набора подготовленных к решению задач.
В общем случае процесс решения дифференциального уравнения путем моделирования состоит из следующих этапов:
1) приведение дифференциального уравнения к виду, удобному для моделирования;
при этом исходное уравнение, подлежащее воспроизведению, называют моделируемым, а уравнение, описывающее связь между входными и выходными величинами моделирующего устройства — моделирующим или машинным уравнением;
2) выбор масштабов машинного уравнения; под масштабами понимаются отношения математических величин к воспроизводящим их физическим величинам;
если некоторая математическая переменная величина Х изображается физической величиной, например, напряжением U, то масштаб К, величины Х (или масштаб Кц величины U) определяется выражением Kх,=Ku=X/U, т.е. масштаб представляет собой число единиц математической величины, соответствующее одной единице физической величины, моделирующей первую;
3) соединение вычислительных блоков для воспроизведения машинного уравнения (в EWB — подготовка схемы модели);
4) проведение моделирования с регистрацией результатов с последующим переходом при помощи ранее выбранных масштабов от переменных величин модели к переменным величинам моделируемой системы-оригинала.
Перечисленные этапы часто относят к так называемому методу моделирования по уравнению. Он позволяет не только решать различные уравнения, но и исследовать системы автоматического управления, для которых уже заранее выбраны все параметры звеньев. Дальнейшим развитием этого метода является метод структурного моделирования, который позволяет решать более сложные задачи выбора параметров структурных звеньев системы-оригинала (см. разд. 14.5).
В качестве примера рассмотрим моделирование последовательного колебательного контура, показанного в верхней части рис. 14.3 и состоящего из катушки индуктивности L с активным сопротивлением R и конденсатора Ck. В нижней части рис. 14.3 изображена электронная модель этого же контура на решающих элементах: сумматоре на ОУ 1, двух интеграторах на ОУ 2 и 3 и инвертирующем усилителе на ОУ 4. Позиционное обозначение резисторов принято в соответствии с рекомендациями [29]: порядковый номер резистора в цепи обратной связи совпадает с номером ОУ, токозадающие резисторы имеют двухзначный номер, первым идет номер соответствующего ОУ, вторым — порядковый номер резистора данной группы. Для конденсаторов интеграторов можно использовать такой же принцип формирования позиционных обозначений, однако в связи с тем, что, как правило, в интеграторах моделирующих установок они имеют одинаковое номинальное значение (в данном случае 1мкФ), то они имеют и одинаковое позиционное обозначение. При обозначении выходных напряжений решающих элементов используется тот же принцип, для наглядности в скобках указывается также и номер соответствующей производной. Для регистрации результатов моделирования в схеме на рис. 14.3 используется осциллограф: канал А — для регистрации напряжения на конденсаторе Ck, канал В — для регистрации напряжения на выходе модели. В качестве источника возмущающего сигнала в рассматриваемом случае используется источник постоянного напряжения U, однако в общем случае это может быть любая функция времени.
Запишем дифференциальное уравнение колебательного контура в следующем виде:

Приведем уравнение (14.4) к виду (14.3)

Как следует из (14.5),.модель колебательного контура должна содержать сумматор (в схеме на рис. 14.3 он выполнен на ОУ 1) и два интегратора (ОУ 2,3). Поскольку сигнал на выходе ОУ 2 имеет полярность, совпадающую с полярностью сигнала на входе сумматора на ОУ 1, то для обеспечения устойчивости модели выход интегратора на ОУ 2 соединен со входом сумматора через инвертирующий усилитель на ОУ 4.
Составим уравнения для каждого решающего блока:

для первого интегратора


для второго интегратора

для инвертирующего усилителя

Разрешая систему уравнений (14.6) — (14.9) относительно величины U3, являющейся в данном случае искомой, получим:

В общем случае величина U3 может представлять исходную переменную (в данном случае — напряжение на конденсаторе Ck) в некотором масштабе, то же самое относится и к независимой переменной (времени) и возмущающему воздействию Uo. Поэтому в уравнение (14.10) необходимо ввести масштабные коэффициенты, которые определяются очевидными уравнениями преобразования:

где М„ — масштаб представления искомой величины Х в виде напряжения; My — масштаб представления возмущающего воздействия Uo; М, — масштаб времени.
С учетом соотношений (14.11) уравнение (14.10) запишется в виде:

В таком же виде запишем исходное уравнение (14.4):

Очевидно, что из условия идентичности оригинала и его модели коэффициенты при соответствующих переменных в уравнениях (14.12) и (14.13) должны быть одинаковыми, т.е.
Из сравнения коэффициентов в правой части каждого уравнения следует требование Мх=Му. Кроме того, из схемы на рис. 14.3 видно, что K11=K12=K13=K41=1. Примем для упрощения последующих расчетов Mt=l. В таком случае условия (14.14) запишем в следующем виде: K21=R/L; K21-K31=l/(LCk) или с учетом обозначений для К21 и К31
R21=L/RC; R31=RCk/C. (14.15)
Выражения (14.15) позволяют выбрать параметры интеграторов модели с использованием параметров оригинала. При указанных на схеме номинальных значениях этих параметров получаем R21=10 кОм и R31=100 Ом.
Перед проведением моделирования необходимо включить режим анализа переходных процессов и установить опцию для паузы после заполнения экрана осциллографа (меню Circuit/Analysis Options). Результаты моделирования показаны на рис. 14.4, откуда видно, что форма и амплитуда сигналов на емкости конденсатора Ск колебательного контура и на выходе его модели совпадают. Из рис. 14.4 видно также, что период затухающих колебаний колебательного переходного процесса равен Т=Т2-Т1=6,48 мс близок к расчетному с использованием формулы
Контрольные вопросы я задания
1. В чем заключается различие между физическим и математическим моделированием?
2. Какие средства вычислительной техники могут быть использованы при математическом моделировании?
3. Какие методы решения дифференциальных уравнений используются при их моделировании с помощью EWB?
4. Что такое «структурное моделирование» и моделирование «по уравнению»? Какой метод использован при подготовке модели на рис. 14.1.
5. Из сравнения рис. 14.2 и 14.3 установите, каким образом в моделях вводятся коэффициенты дифференциального уравнения (в частности, коэффициенты В1 и ВО)? Обязательно ли при этом использование перемножающих устройств?
6. Из осциллограмм на рис. 14.4 видно, что переходной процесс в резонансном контуре имеет колебательный характер. Известно (это следует из решения уравнения (14.13)), что вид переходного процесса в колебательном контуре определяется соотношениями 
7. В модели на рис. 14.3 источник постоянного напряжения U замените на источник переменного напряжения с амплитудой 1 В и частотой, равной резонансной частоте контура, и проведите моделирование.
Понятие же «физического вакуума» в релятивистской квантовой теории поля подразумевает, что во-первых, он не имеет физической природы, в нем лишь виртуальные частицы у которых нет физической системы отсчета, это «фантомы», во-вторых, «физический вакуум» — это наинизшее состояние поля, «нуль-точка», что противоречит реальным фактам, так как, на самом деле, вся энергия материи содержится в эфире и нет иной энергии и иного носителя полей и вещества кроме самого эфира.
В отличие от лукавого понятия «физический вакуум», как бы совместимого с релятивизмом, понятие «эфир» подразумевает наличие базового уровня всей физической материи, имеющего как собственную систему отсчета (обнаруживаемую экспериментально, например, через фоновое космичекое излучение, — тепловое излучение самого эфира), так и являющимся носителем 100% энергии вселенной, а не «нуль-точкой» или «остаточными», «нулевыми колебаниями пространства». Подробнее читайте в FAQ по эфирной физике.
http://habr.com/ru/post/418139/
http://www.bourabai.ru/toe/ch2-3/14_1.htm
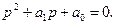
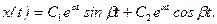
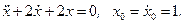
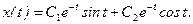
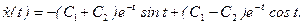
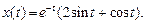
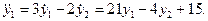
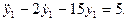
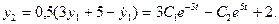
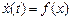 , сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.
, сравнить их с теоретическими графиками. Варьировать шаг и метод интегрирования.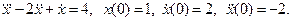
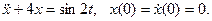
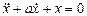 имеет вид:
имеет вид: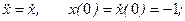
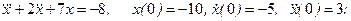
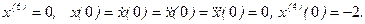
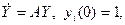 если матрица A имеет вид
если матрица A имеет вид