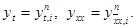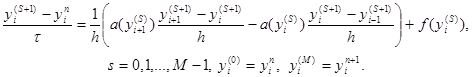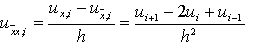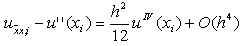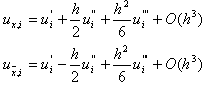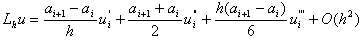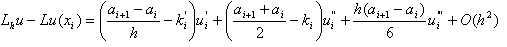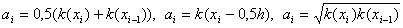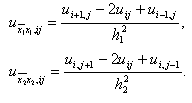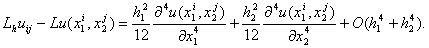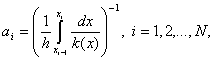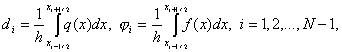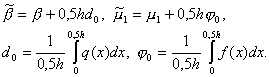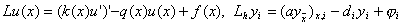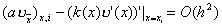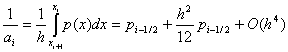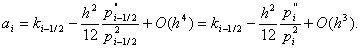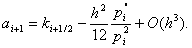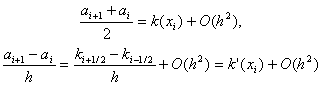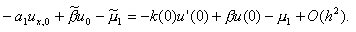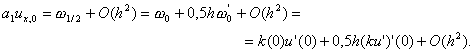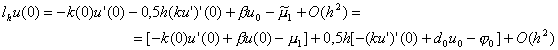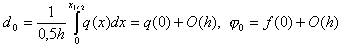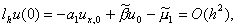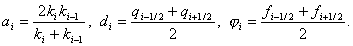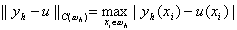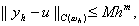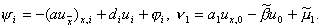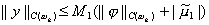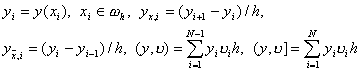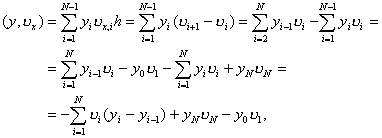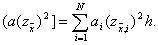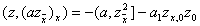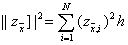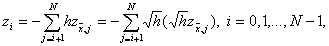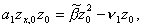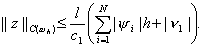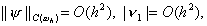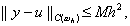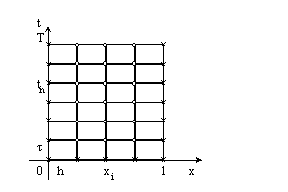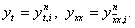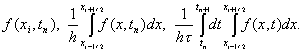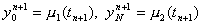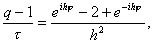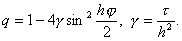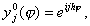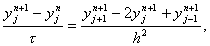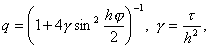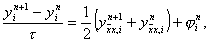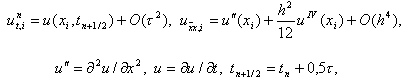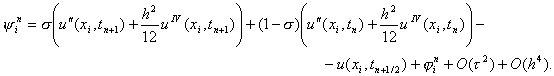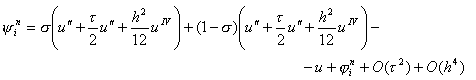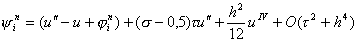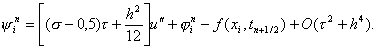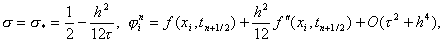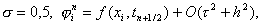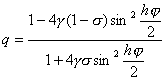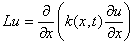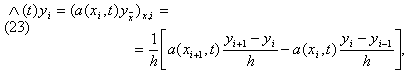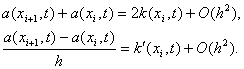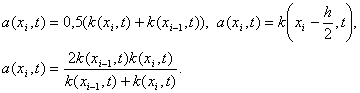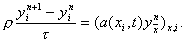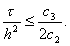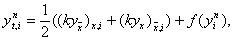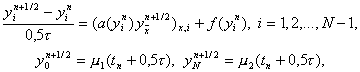Шеститочечная схема для уравнения теплопроводности

Разностные схемы для уравнения теплопроводности

3.1. Исходная задача. Будем рассматривать следующую первую краевую задачу для уравнения теплопроводности с постоянными коэффициентами. В области <0 n _i = y(x_i, t_n),

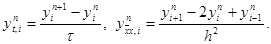Иногда для упрощения записи индексы i и n будем опускать, обозначая

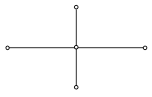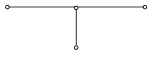
Чтобы аппроксимировать уравнение (1) в точке (x_i, t_n), введем шаблон, изображенный на рисунке и состоящий из четырех узлов (x_i±1, t_n), (x_i, t_n), (x_i, t_n+1). Производную ¶u/¶t заменим в точке (x_i, t_n) разностным отношением y n _{t, i}, а производную ¶ 2 u/¶ 2 x – второй разностной производной y n _{xx, i}. Правую часть f(x, t) заменим приближенно сеточной функцией j n _i, в качестве j n _i можно взять одно из следующих выражений:

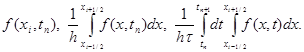В результате получим разносное уравнение

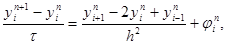которое аппроксимирует исходное дифференциальное уравнение в точке (x_i, t_n) с первым порядком по t и вторым порядком по h при условии, что разность j n _i – f(x_i, t_n) имеет тот же порядок малости.

Под разностной схемой понимается совокупность разностных уравнений, аппроксимирующих основное дифференциальное уравнение во всех внутренних узлах сетки и дополнительные (начальные и граничные) условия – в граничных узлах сетки. Разностную схему по аналогии с дифференциальной задачей будем называть также разностной задачей. В данном случае разностная схема имеет вид

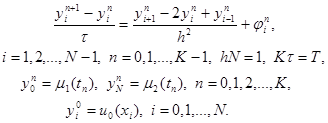Эта схема представляет собой систему линейных алгебраических уравнений с числом уравнений, равным числу неизвестных. Находить решение такой системы следует по слоям. Решение на нулевом слое задано начальными условиями y 0 _i = u₀(x_i), i = 0, 1,…, N. Если решение y n _i, i = 0, 1,…, N, на слое n уже найдено, то решение y_i n+1 на слое n+1 находится по явной формуле

а значения доопределяются из граничных

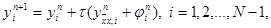условий. По этой причине схема (6) называется явной разностной схемой. Несколько позже мы познакомимся и с неявными схемами, в которых для нахождения y_i n+1 при заданных y_i n требуется решать систему уравнений.

Погрешность разностной схемы (6) определяется как разность z_i n = y_i n – u(x_i, t_n) между решением задачи (6) и решением исходной задачи (1) – (3). Подставляя в (6) y_i n = z_i n + u(x_i, t_n), получим уравнение для погрешности

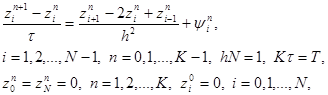где – погрешность аппроксимации разностной

схемы (6) на решении задачи (1) – (3), y _i n = O( t + h 2 ). Можно оценить решение z_i n уравнения (8) через правую часть y_i n и доказать тем самым сходимость разностной схемы (6) с первым порядком по t и вторым – по h. Однако это исследование мы отложим, а сейчас на примере схемы (6) продемонстрируем один распространенный прием исследования разностных схем с постоянными коэффициентами, называемый методом гармоник. Хотя данный метод не является достаточно обоснованным, в частности не учитывает влияния граничных условий и правых частей, он позволяет легко найти необходимые условия устойчивости и сходимости разностных схем. Покажем, например, что явную схему (6) можно применять лишь при условии t £ 0,5h 2 , означающем, что шаг по времени надо брать достаточно малым.

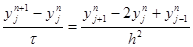т.е. однородное уравнение, соответствующее (5). Будем искать частные решения (9), имеющие вид

y_j n ( j ) = q n e ijh j , (10)

где i – мнимая единица, j – любое действительное число и q – число, подлежащее определению. Подставляя (10) в уравнение (9) и сокращая на e ijh j , получим

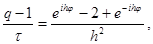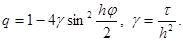Начальные условия соответствующие решениям вида (10) (их называют гармониками), ограничены. Если для некоторого j множитель q станет по модулю больше единицы, то решение вида (10) будет неограниченно возрастать при n®¥. В этом случае разностное уравнение (9) называется неустойчивым, поскольку нарушается непрерывная зависимость его решения от начальных условий. Если же |q| £ 1 для всех действительных j, то все решения вида (10) ограничены при любом n и разностное уравнение (9) называется устойчивым. В случае неустойчивости найти решение разностной задачи (6) по формулам (7) практически невозможно, так как погрешности (например погрешности округления), внесенные в начальный момент времени, будут неограниченно возрастать при увеличении n. Такие разностные схемы называются неустойчивыми.

Для уравнения (9) неравенство |q| £ 1 выполняется согласно (11) при всех j тогда и только тогда, когда g £ 0,5. Таким образом, использование схемы (6) возможно лишь при выполнении условия t £ 0,5h 2 . Разностные схемы, устойчивые лишь при некотором ограничении на отношение шагов по пространству и по времени, называются условно устойчивыми. Следовательно, схема (6) возможно устойчива, причем условие устойчивости имеет вид t/h 2 £ 0,5. Условно устойчивые схемы для уравнений параболического типа используются редко, так как они накладывают слишком сильное ограничение на шаг по времени. Действительно, пусть, например, h = 10 -2 . Тогда шаг t не должен превосходить 0,5 * 10 -4 , и для того чтобы вычислить решение y_j n при t = 1, надо взять число шагов по времени n = t -1 ³ 2 * 10 4 , т.е. провести не менее 2 * 10 4 вычислений по формулам (7).

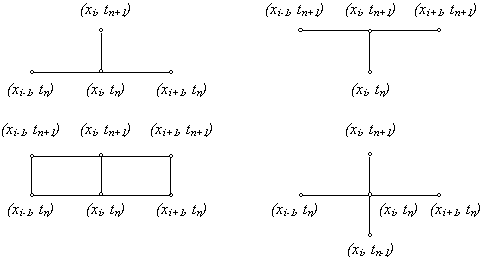
3.3. Неявные схемы. Чисто неявной разностной схемой для уравнения теплопроводности теплопроводности (схемой с опережением) называется разностная схема, использующая шаблон (x_i, t_n), (x_{i ± 1} , t_n+1), (x_i, t_n+1) и имеющая вид

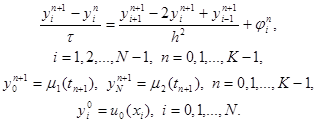Здесь j n _i = f(x_i, t_n+1) + O( t + h 2 ). Схема имеет первый порядок аппроксимации по t и второй – по h. Решение системы (12) находится, как и в случае явной схемы, по слоям, начиная с n = 1. Однако, теперь, в отличие от явной схемы, для нахождения y i _n+1 по известным y_i n требуется решить систему уравнений

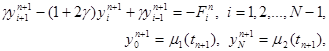где g = t /h 2 , F_i n = y_i n + t j _i n . Эту систему можно решать методом прогонки, так как условия устойчивости прогонки выполнены.

Для исследования устойчивости разностной схемы (12) будем искать частные решения уравнения

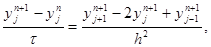имеющие вид (10). Тогда получим

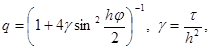следовательно, |q| £ 1 при любых j , t , h. Таким образом, схема (12) абсолютно устойчива, т.е. устойчива при любых шагах t и h. Абсолютная устойчивость является основным условием неявных схем. Теперь уже не надо брать шаг t слишком малым, можно взять, например, t = h = 10 -2 . Величина шагов сетки t , h определяются теперь необходимой точностью расчета, а не соображениями устойчивости.

Шеститочечной симметричной схемой называется разностная схема

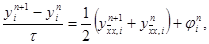
для которой начальные и граничные условия задаются так же, как и в схеме (12). Эта схема использует шеститочечный шаблон, изображенный на рисунке.

Обобщением трех рассмотренных схем является однопараметрическое семейство схем с весами. Зададим произвольный действительный параметр s и определим разностную схему

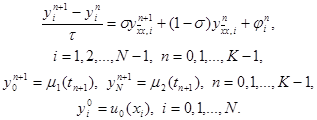При s = 0 получим отсюда явную схему, при s = 1 – чисто неявную схему и при s = 0,5 – симметричную схему (14). Исследуем погрешность аппроксимации схемы (15) на решении исходной задачи (1) – (3). Представим решение задачи (15) в виде y_i n = u(x_i, t_n) + z_i n , где u(x_i, t_n) – точное решение дифференциальной задачи (1) – (3). Тогда для погрешности получим систему уравнений

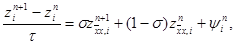i = 1, 2,…, N – 1, n = 0, 1,…, K – 1,

Сеточная функция y_i n , входящая в правую часть уравнения (16) и равная

(17)

называется погрешностью аппроксимации схемы (15) на решении задачи (1) – (3). Получим первые члены разложения функции y_i n по степеням h и t. Будем разлагать все функции, входящие в выражение для y_i n , по формуле Тейлора в точке (x_i, t_n + 0,5t). Учитывая разложения

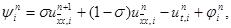
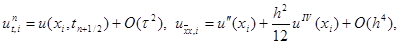
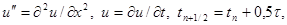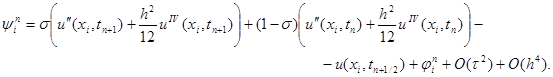Отсюда, проводя разложение в точке (x_i, t_n+1/2) и обозначая u = u (x_i, t_n+1/2), будем иметь

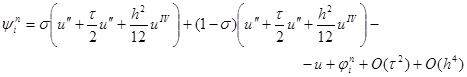и, перегруппировывая слагаемые, получим, что

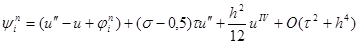Учитывая уравнение (1) u’’ – u = – f и следствие из него u IV – u’’ = –f’’, окончательно можно записать, что

Из формулы (18) можно сделать следующие выводы. Если

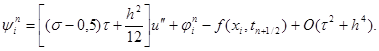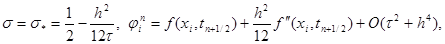
то схема (15) имеет второй порядок аппроксимации по t и четвертый – по h. Такая схема называется схемой повышенного порядка аппроксимации. Если

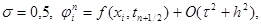то схема (15) имеет второй порядок аппроксимации по t и по h. При остальных значениях s и при j _i n º 0 в виде (10), то получим

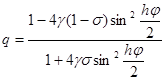и |q| £ 1 при всех j, если

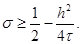Отсюда видно, в частности, что все схемы с s ³ 0,5 абсолютно устойчивы. Схема повышенного порядка аппроксимации (s = s_*) также абсолютно устойчива, что проверяется непосредственно.

При s ¹ 0 разностная схема (15) является неявной схемой. Для нахождения решения y_i n+1 по заданным y_i n требуется решать систему уравнений

где

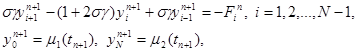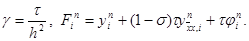
Система (20) решается методом прогонки. Условия устойчивости прогонки при s ¹ 0 сводятся к неравенству

|1 + 2 s g | ³ 2 | s | g

и выполнены при s ³ – 1/(4g). Последнее неравенство следует из условия устойчивости (19) разностной схемы.

3.4. Уравнения с переменными коэффициентами и линейные уравнения. Рассмотрим первую краевую задачу для уравнения теплопроводности с переменными коэффициентами

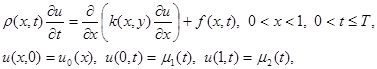где r (x, t), k(x, t), f(x, t) – достаточно гладкие функции, удовлетворяющие условиям

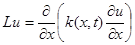Дифференциальное выражение при каждом

фиксированном t аппроксимируем в точке (x_i, t) так же, как и в стационарном случае, разностным отношением

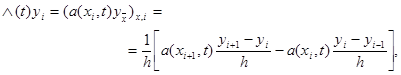где разностный коэффициент теплопроводности a(x_i, t) должен удовлетворять условиям второго порядка аппроксимации

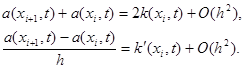Наиболее употребительны следующие выражения для a(x_i, t):

Разностная схема с весами для задачи (21) имеет вид

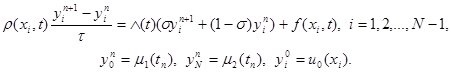Здесь в качестве t можно взять любое значение t Î [t_n, t_n+1], например t = t_n + 0,5 t. Если в уравнении (24) t = t_n + 0,5 t , s = 0,5, то схема (24) имеет второй порядок аппроксимации по t и по h. При остальных значениях s и t выполняется первый порядок аппроксимации по t и второй – по h.

При исследовании устойчивости разностных схем с переменными коэффициентами иногда применяется принцип замороженных коэффициентов, сводящий задачу к уравнению с постоянными коэффициентами. Рассмотрим явную схему, соответствующую уравнению (24) с s = 0 и f(x_i, t) º 0, т.е. схему

Предположим, что коэффициенты r (x_i, t), a(x_i, t) – постоянные, r (x_i, t) º r = const, a(x_i, t) º a = const. Тогда уравнение (25) можно записать в виде

или

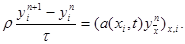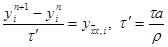
Из п.2 известно, что последнее уравнение устойчиво при t ’ £ 0,5h 2 , т.е. при

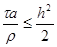Принцип замороженных коэффициентов утверждает, что схема (25) устойчива, если условие (26) выполнено при всех допустимых значениях a(x_i, t), r (x_i, t), т.е. если при всех x, t выполнены неравенства

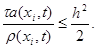Если известно, что 0 0, то неравенство (27) будет выполнено при

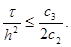Строгое обоснование устойчивости схемы (25) будет дано в примере 2 из главы 2.

Если параметр s ³ 0,5, то из принципа замороженных коэффициентов следует абсолютная устойчивость схемы (24).

Рассмотрим теперь первую краевую задачу для нелинейного уравнения теплопроводности

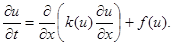В случае нелинейных уравнений, когда заранее неизвестны пределы изменения функции k(u), избегают пользоваться явными схемами. Чисто неявная схема, линейная относительно y_i n+2 , i = 1, 2,…, N – 1, имеет вид

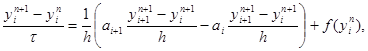где a_i = 0,5 (k(y n _i) + k(y n _i-1)). Эта схема абсолютно устойчива, имеет первый порядок аппроксимации по t и второй – по h. Решение y_i n+1 , i = 1, 2,…, N – 1, находится методом прогонки. Заметим, что схему (29) можно записать в виде

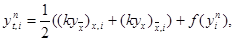Часто используется нелинейная схема

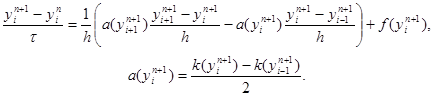Для реализации этой схемы необходимо применить тот или иной итерационный метод. Например такой:

Здесь s – номер итерации. Как видим, нелинейные коэффициенты берутся с предыдущей итерации, а в качестве начального приближения для y_i n+1 выбирается y_i n . Это начальное приближение тем лучше, чем меньше шаг t. Число итераций M задается из соображений точности. В задачах с гладкими коэффициентами при k(u) ³ c₁ > 0 часто бывает достаточно провести две – три итерации. Значения y_i (S+1) на новой итерации находятся из системы (31) методом прогонки. При M = 1 итерационный метод (31) совпадает с разностной схемой (29).

Для приближенного решения нелинейного уравнения (28) применяются также схемы предиктор – корректор второго порядка точности, аналогичные методу Рунге – Кутта для обыкновенных дифференциальных уравнений. Здесь переход со слоя n на слой n+1 осуществляется в два этапа. Приведем пример такой схемы. На первом этапе решается неявная линейная система уравнений

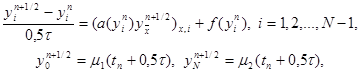из которой находятся промежуточные значения y_i n+1/2 , i = 0, 1,…, N. Затем на втором этапе используется симметричная шеститочечная схема для уравнения (28), в которой нелинейные коэффициенты a(y), f(y) вычисляются при y = y_i n+1/2 , т.е. схема

Разностные аппроксимации

Разностные аппроксимации

1.Примеры разностных аппроксимаций.

Различные способы приближенной замены одномерных дифференциальных уравнений разностными изучались ранее. Напомним примеры разностных аппроксимаций и введем необходимые обозначения. Будем рассматривать равномерную сетку с шагом h , т.е. множество точек

Пусть u(x) – достаточно гладкая функция, заданная на отрезке [x i-1 , x i+1 ]. Обозначим

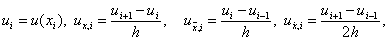
называются соответственно правой, левой и центральной разностными производными функции u(x) в точке x i , т.е. при фиксированном x i и при h ® 0 (тем самым при i ® ¥ ) пределом этих отношений является u’(x i ) . Проводя разложение по формуле Тейлора, получим

u x,i – u’(x i ) = 0,5hu’’(x i ) + O(h 2 ),

u x,i – u’(x i ) = -0,5hu’’(x i ) + O(h 2 ),

u x,i – u’(x i ) = O(h 2 ),

Отсюда видно, что левая и правая разностные производные аппроксимируют u’(x) с первым порядком по h , а центральная разностная производная – со вторым порядком. Нетрудно показать, что вторая разностная производная

аппроксимирует u’’(x i ) со вторым порядком по h , причем справедливо разложение

Рассмотрим дифференциальное выражение

(1)

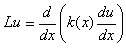
с переменным коэффициентом k(x) . Заменим выражение (1) разностным отношением

(2)

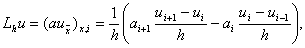
где a=a(x) – функция, определенная на сетке w h . Найдем условия, которым должна удовлетворять функция a(x) для того, чтобы отношение (au x ) x,i аппроксимировало (ku’)’ в точке x i со вторым порядком по h . Подставляя в (2) разложения

где u i ’ = u’(x i ) , получим

С другой стороны, Lu = (ku’)’ = ku’’ + k’u’,

т.е.

Отсюда видно, что L h u–Lu = O(h 2 ) , если выполнены условия

(3)

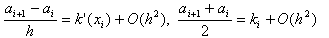
Условия (3) называются достаточными условиями второго порядка аппроксимации . При их выводе предполагалось, что функция u(x) имеет непрерывную четвертую производную и k(x) – дифференцируемая функция. Нетрудно показать, что условиям (3) удовлетворяют, например, следующие функции:

Заметим, что если положить a i = k(x i ), то получим только первый порядок аппроксимации.

В качестве следующего примера рассмотрим разностную аппроксимацию оператора Лапласа

(4)

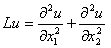
Введем на плоскости (x 1 , x 2 ) прямоугольную сетку с шагом h 1 по направлению x 1 и с шагом h 2 по направлению x 2 , т.е. множество точек

Из предыдущих рассуждений следует, что разностное выражение

(5)

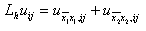
аппроксимирует дифференциальное выражение (4) со вторым порядком, т.е. L h u ij – Lu(x i 1 , x j 2 ) = O(h 2 1 ) + O(h 2 2 ). Более того, для функций u(x 1 , x 2 ), обладающих непрерывными шестыми производными, справедливо разложение

Разностное выражение (5) называется пятиточечным разностным оператором Лапласа , так как оно содержит значения функции u(x 1 , x 2 ) в пяти точках сетки, а именно в точках (x 1 i , x 2 j ), (x 1 i ± 1 , x 2 j ), (x 1 i , x 2 j ± 1 ). Указанное множество точек называется шаблоном разностного оператора. Возможны разностные аппроксимации оператора Лапласа и на шаблонах, содержащих большее число точек.

2. Исследование аппроксимации и сходимости

2.1. Аппроксимация дифференциального уравнения.

Ранее рассматривалась краевая задача

(k(x) u’(x))’ – q(x) u(x) + f(x) = 0, 0 (1)

– k(0) u’(0) + b u(0) = m 1 , u(l) = m 2 , (2)

k(x) ³ c 1 > 0, b ³ 0,

для которой интегро-интерполяционным методом была построена разностная схема

(3), (4)

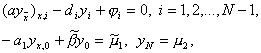
Обозначим через Lu(x) левую часть уравнения (1) и через L h y i – левую часть уравнения (3), т.е.

Пусть u (x) – достаточно гладкая функция и u (x i ) – ее значение в точке x i сетки

Говорят, что разностный оператор L h аппроксимирует дифференциальный оператор L в точке x=x i , если разность L h u i – L h u (x i ) стремится к нулю при h ® 0. В этом случае говорят также, что разностное уравнение (3) аппроксимирует дифференциальное уравнение (1).

Чтобы установить наличие аппроксимации, достаточно разложить по формуле Тейлора в точке x=x i значения u i ± 1 = u (x i ± h) , входящие в разностное выражение L h u i . Большая часть этой работы проделана в предыдущей главе, где показано, что при условиях

(8)

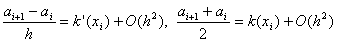
Если кроме того, докажем, что

d i = q(x i ) + O(h 2 ), j i = f(x i ) + O(h 2 ) (9)

то тем самым будет установлено, что оператор L h аппроксимирует L со вторым порядком по h , т.е.

L h u i – L u (x i ) = O(h 2 ), i = 1, 2,…, N–1 (10)

Итак, доказательство второго порядка аппроксимации сводится к проверке сводится к проверке условий (8), (9) для коэффициентов (5), (6). Проверим сначала выполнение условий (8). Обозначая p(x) = k -1 (x) , получим

т.е. условия (8) выполнены. Условия (9) выполнены в силу того, что замена интегралов (6) значениями q i , f i соответствует приближенному вычислению этих интегралов по формуле прямоугольников с узлом в середине отрезка интегрирования.

2.2. Аппроксимация граничного условия.

Исследуем погрешность аппроксимации разностного граничного условия (4). Обозначим l h u (0) = –a 1 u x, 0 + b u 0 . Если u (x) – произвольная достаточно гладкая функция, то очевидно

l h u (0) = –k(0) u ’(0) + b u (0) + O(h) ,

т.е. имеет место аппроксимация первого порядка по h . Однако если u =u(x) – решение задачи (1), (2), то разностное граничное условие (4) имеет второй порядок аппроксимации, т.е.

Докажем последнее утверждение. Используя разложение

u x, 0 = (u 1 – u 0 )/h = u’(x 1/2 ) + O(h 2 ), x 1/2 = 0,5h,

a 1 = k 1/2 + O(h 2 )

Учитывая граничное условие (2), получаем

l h u(0) = 0,5h [– (ku’)’(0) + d 0 u 0 – j 0 ] + O(h 2 ) .

Выражение, стоящее в квадратных скобках, преобразуем, учитывая уравнение (1), к виду

– (ku’)’(0) + d 0 u 0 – j 0 = – (ku’)’(0) + q(0)u(0) – f(0) +

+ (d 0 – q(0))u 0 – (f(0) – j 0 ) = (d 0 – q(0))u 0 – (f(0) – j 0 ) .

что и требовалось доказать.

Таким образом, при достаточной гладкости коэффициентов k(x), q(x), f(x) и решения u(x) разностная схема (10) аппроксимирует исходную задачу (2) со вторым порядком по h .

При практическом использовании разностной схемы для нахождения ее коэффициентов не обязательно вычислять интегралы (4), (6) точно. Можно воспользоваться коэффициентами, полученными путем замены этих интегралов квадратурными формулами, имеющими точность O(h 2 ) и выше. Например, в результате применения формулы прямоугольников получим следующие коэффициенты: a i = k(x i – 0,5h), d i = q(x i ), j i = f(x i ).

Применяя формулу трапеций, получим

Представление коэффициентов разностной схемы в виде интегралов (4), (6) оказывается полезным при исследовании сходимости в случае разрывных функций k(x), q(x), f(x) .

2.3. Уравнение для погрешности.

Решение y i = y(x i ) разностной задачи (3), (4) зависит от шага h сетки, y(x i ) = y h (x i ) . По существу, мы имеем семейство решений , зависящее от параметра h . Говорят, что решение y h (x) разностной задачи сходится к решению u(x) исходной дифференциальной задачи, если при h ® 0 погрешность y h (x i ) – u(x i ), i = 0, 1,…, N , стремится к нулю в некоторой норме. В настоящем параграфе в качестве такой нормы будем брать норму в сеточном пространстве C( w h ) , т.е. положим

Говорят, что разностная схема имеет m-й порядок точности (или сходится с порядком m ), если

где m>0, M>0 – константы, не зависящие от h .

Выше было установлено, что схема (3), (4) имеет второй порядок аппроксимации. Докажем теперь, что эта схема имеет и второй порядок точности. Для этого прежде всего выпишем уравнение, которому удовлетворяет погрешность z i = y i – u(x i ) . Поставим y i = z i + u(x i ) в уравнения (3), (4). Тогда получим уравнения

(11), (12)

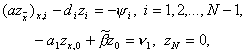
Функция y i , входящая в правую часть уравнения (11), называется погрешностью аппроксимации дифференциального уравнения (1) разностным уравнением (3) на решении задачи (1), (2). В п.1 было доказано, что y i = O(h 2 ) при h ® 0, i=1, 2,…, N–1 . Аналогично, величина n 1 является по определению погрешностью аппроксимации краевого условия (2) разностным краевым условием (4) на решении задачи (1), (2), причем n 1 =O(h 2 ) . Таким образом, структура уравнений для погрешности (11), (12) та же, что и у разностной схемы (3), (4), отличаются только правые части.

Чтобы доказать сходимость разностной схемы, оценим решение задачи (11), (12) через правые части y i , n 1 , т.е. получим неравенство вида

(13)

с константой M 1 , не зависящей от h . Из этого неравенства и будет следовать, что

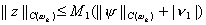
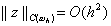
Отметим, что неравенства вида (13), называемые априорными оценками, нашли широкое применение в теории разностных схем. Поскольку структура для погрешности (11), (12) та же, что и у разностной схемы (3), (4), а отличаются только правые части, то оценка (13) выполняется одновременно с аналогичной оценкой

для разностной схемы (3), (4) при m 2 = 0 . Последняя оценка выражает устойчивость решения разностной задачи по правым частям j и m 1 .

2.4. Разностные тождества и неравенства.

Для того, чтобы доказать неравенство (13), нам потребуются некоторые разностные тождества и неравенства. Будем рассматривать сеточные функции, заданные на сетке (7). Обозначим

Справедливо следующее разностное утверждение:

(y, u x ) = –( u , y x ) + y N u N – y 0 u 1 . (14)

что и требовалось доказать. Тождество (14) называется формулой суммирования по частям .

Подставляя в (14) вместо u выражение az x и вместо y функцию z, получаем первую разностную формулу Грина

(15)

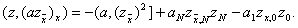
Здесь

В частности, если z N = 0 (как в задаче (11), (12)), то получим

(16)

и докажем, что для любой сеточной функции z i , удовлетворяющей условию z N = 0 , справедливо неравенство

(17)

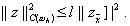
Для доказательства воспользуемся тождеством

и применим неравенство Коши-Буняковского

Откуда сразу следует неравенство (17).

2.5. Доказательство сходимости.

Возвращаясь к доказательству сходимости схемы (3), (4), получим тождество, которому удовлетворяет погрешность z i = y i – u(x i ) . Для этого умножим уравнение (11) на hz i и просуммируем по i от 1 до N–1 . Тогда получим

Отсюда, применяя разностную формулу Грина (16), получим

Далее, согласно (12) имеем

следовательно, справедливо тождество

(18)

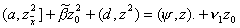
Из этого тождества и будет сейчас выведено требуемое неравенство вида (13).

Заметим прежде всего, что если

k(x) ³ c 1 > 0, b ³ 0, q(x) ³ 0,

то коэффициенты разностной схемы (3), (4) удовлетворяют неравенствам

a i ³ c 1 > 0, b ³ 0, d i ³ 0. (19)

Это утверждение сразу следует из явного представления коэффициентов (5), (6).

Воспользовавшись (19), оценим слагаемые, входящие в левую часть тождества (18), следующим образом:

Тогда придем к неравенству

(20)

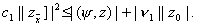
Оценим сверху правую часть этого неравенства. Будем иметь

Подставляя эту оценку в (20) и учитывая неравенство (17), получим

(21)

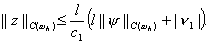
Посколькуиз неравенства следует,

что погрешность z i = y i – u(x i ) также является величиной O(h 2 ) при h ® 0. Итак, справедливо следующее утверждение.

Пусть k(x) – непрерывно дифференцируемая и q(x), f(x) – непрерывные функции при x Î [0, l], решение u(x) задачи (1), (2) обладает непрерывными четвертыми производными. Пусть коэффициенты разностной схемы (3), (4) удовлетворяют условиям (8), (9), (19). Тогда решение разностной задачи (3), (4) сходится при h ® 0 к решению исходной дифференциальной задачи (1), (2) со вторым порядком по h, так что выполняется оценка

где M – постоянная, не зависящая от h.

3. Разностные схемы для уравнения теплопроводности

3.1. Исходная задача.

Будем рассматривать следующую первую краевую задачу для уравнения теплопроводности с постоянными коэффициентами. В области <0 £ T>требуется найти решение уравнения

(1)

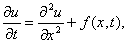
удовлетворяющее начальному условию

и граничным условиям

u(0, t) = m 1 (t), u(1, t) = m 2 (t). (3)

Здесь u0(x), m 1 (t), m 2 (t) – заданные функции. Известно, что при определенных предположениях гладкости решение задачи (1)–(3) существует и единственно. В дальнейшем при исследовании аппроксимации разностных схем будем предполагать, что решение u(x, t) обладает необходимым по ходу изложения числом производных по x и по t. Решение задачи (1) – (3) удовлетворяет принципу максимума и тем самым непрерывно зависит от начальных и граничных данных.

3.2. Явная схема.

Как всегда, для построения разностной схемы надо прежде всего ввести сетку в области изменения независимых переменных и задать шаблон, т.е. множество точек сетки, участвующих в аппроксимации дифференциального выражения. Введем сетку по переменному x такую же, как в предыдущей главе, т.е.

и сетку по переменному t с шагом t , которую обозначим

Точки (x i , t n ), i = 0, 1,…, N, n = 0, 1,…, K , образуют узлы пространственно-временной сетки w h, t = w h x w t . Узлы (x i , t n ) , принадлежащие отрезкам I 0 = <0 £ x £ 1, t = 0>, I 1 = , I 2 = , называются граничными узлами сетки w h, t , а остальные узлы – внутренними. На рисунке граничные узлы обозначены крестиками, а внутренние – кружочками.

Слоем называется множество всех узлов сетки w h, t , имеющих одну и ту же временную координату. Так, n-м слоем называется множество узлов

(x 0 , t n ), (x 1 , t n ),…, (x N , t n ) .

Для функции y(x, t) , определенной на сетке w h, t , введем обозначения y n i = y(x i , t n ) ,

(4)

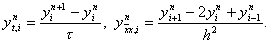
Иногда для упрощения записи индексы i и n будем опускать, обозначая

Чтобы аппроксимировать уравнение (1) в точке (x i , t n ), введем шаблон, изображенный на рисунке и состоящий из четырех узлов (x i ± 1 , t n ), (x i , t n ), (x i , t n+1 ). Производную ¶ u/ ¶ t заменим в точке (x i , t n ) разностным отношением y n t, i , а производную ¶ 2 u/ ¶ 2 x – второй разностной производной y n xx, i . Правую часть f(x, t) заменим приближенно сеточной функцией j n i , в качестве j n i можно взять одно из следующих выражений:

В результате получим разносное уравнение

(5)

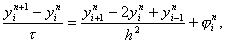
которое аппроксимирует исходное дифференциальное уравнение в точке (x i , t n ) с первым порядком по t и вторым порядком по h при условии, что разность j n i – f(x i , t n ) имеет тот же порядок малости.

Под разностной схемой понимается совокупность разностных уравнений, аппроксимирующих основное дифференциальное уравнение во всех внутренних узлах сетки и дополнительные (начальные и граничные) условия – в граничных узлах сетки. Разностную схему по аналогии с дифференциальной задачей будем называть также разностной задачей. В данном случае разностная схема имеет вид

(6)

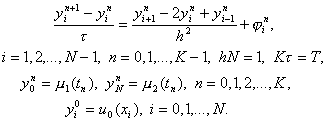
Эта схема представляет собой систему линейных алгебраических уравнений с числом уравнений, равным числу неизвестных. Находить решение такой системы следует по слоям. Решение на нулевом слое задано начальными условиями y 0 i = u 0 (x i ), i = 0, 1,…, N . Если решение y n i , i = 0, 1,…, N , на слое n уже найдено, то решение y i n+1 на слое n+1 находится по явной формуле

(7)

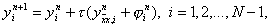
а значениядоопределяются из граничных

условий. По этой причине схема (6) называется явной разностной схемой. Несколько позже мы познакомимся и с неявными схемами, в которых для нахождения y i n+1 при заданных y i n требуется решать систему уравнений.

Погрешность разностной схемы (6) определяется как разность z i n = y i n – u(x i , t n ) между решением задачи (6) и решением исходной задачи (1) – (3). Подставляя в (6) y i n = z i n + u(x i , t n ) , получим уравнение для погрешности

(8)

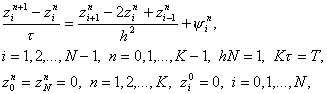
где 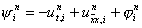– погрешность аппроксимации разностной

схемы (6) на решении задачи (1) – (3), y i n = O( t + h 2 ) . Можно оценить решение z i n уравнения (8) через правую часть y i n и доказать тем самым сходимость разностной схемы (6) с первым порядком по t и вторым – по h. Однако это исследование мы отложим, а сейчас на примере схемы (6) продемонстрируем один распространенный прием исследования разностных схем с постоянными коэффициентами, называемый методом гармоник . Хотя данный метод не является достаточно обоснованным, в частности не учитывает влияния граничных условий и правых частей, он позволяет легко найти необходимые условия устойчивости и сходимости разностных схем. Покажем, например, что явную схему (6) можно применять лишь при условии t £ 0,5h 2 , означающем, что шаг по времени надо брать достаточно малым.

(9)

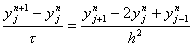
т.е. однородное уравнение, соответствующее (5). Будем искать частные решения (9), имеющие вид

y j n ( j ) = q n e ijh j ,(10)

где i – мнимая единица, j – любое действительное число и q – число, подлежащее определению. Подставляя (10) в уравнение (9) и сокращая на e ijh j , получим

(11)

Начальные условиясоответствующие решениям вида (10) (их называют гармониками), ограничены. Если для некоторого j множитель q станет по модулю больше единицы, то решение вида (10) будет неограниченно возрастать при n ® ¥ . В этом случае разностное уравнение (9) называется неустойчивым, поскольку нарушается непрерывная зависимость его решения от начальных условий. Если же |q| £ 1 для всех действительных j , то все решения вида (10) ограничены при любом n и разностное уравнение (9) называется устойчивым. В случае неустойчивости найти решение разностной задачи (6) по формулам (7) практически невозможно, так как погрешности (например погрешности округления), внесенные в начальный момент времени, будут неограниченно возрастать при увеличении n. Такие разностные схемы называются неустойчивыми.

Для уравнения (9) неравенство |q| £ 1 выполняется согласно (11) при всех j тогда и только тогда, когда g £ 0,5. Таким образом, использование схемы (6) возможно лишь при выполнении условия t £ 0,5h 2 . Разностные схемы, устойчивые лишь при некотором ограничении на отношение шагов по пространству и по времени, называются условно устойчивыми. Следовательно, схема (6) возможно устойчива, причем условие устойчивости имеет вид t /h 2 £ 0,5. Условно устойчивые схемы для уравнений параболического типа используются редко, так как они накладывают слишком сильное ограничение на шаг по времени. Действительно, пусть, например, h = 10 -2 . Тогда шаг t не должен превосходить 0,5 * 10 -4 , и для того чтобы вычислить решение y j n при t = 1 , надо взять число шагов по времени n = t -1 ³ 2 * 10 4 , т.е. провести не менее 2 * 10 4 вычислений по формулам (7).

3.3. Неявные схемы.

Чисто неявной разностной схемой для уравнения теплопроводности теплопроводности (схемой с опережением) называется разностная схема, использующая шаблон (x i , t n ), (x i ± 1 , t n+1 ), (x i , t n+1 ) и имеющая вид

(12)

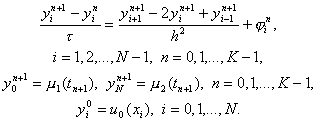
Здесь j n i = f(x i , t n+1 ) + O( t + h 2 ) . Схема имеет первый порядок аппроксимации по t и второй – по h. Решение системы (12) находится, как и в случае явной схемы, по слоям, начиная с n = 1. Однако, теперь, в отличие от явной схемы, для нахождения y i n+1 по известным y i n требуется решить систему уравнений

(13)

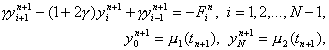
где g = t /h 2 , F i n = y i n + t j i n . Эту систему можно решать методом прогонки, так как условия устойчивости прогонки выполнены.

Для исследования устойчивости разностной схемы (12) будем искать частные решения уравнения

имеющие вид (10). Тогда получим

следовательно, |q| £ 1 при любых j , t , h . Таким образом, схема (12) абсолютно устойчива, т.е. устойчива при любых шагах t и h . Абсолютная устойчивость является основным условием неявных схем. Теперь уже не надо брать шаг t слишком малым, можно взять, например, t = h = 10 -2 . Величина шагов сетки t , h определяются теперь необходимой точностью расчета, а не соображениями устойчивости.

Шеститочечной симметричной схемой называется разностная схема

(14)

для которой начальные и граничные условия задаются так же, как и в схеме (12). Эта схема использует шеститочечный шаблон, изображенный на рисунке.

Обобщением трех рассмотренных схем является однопараметрическое семейство схем с весами. Зададим произвольный действительный параметр s и определим разностную схему

(15)

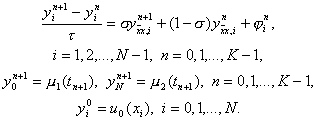
При s = 0 получим отсюда явную схему, при s = 1 – чисто неявную схему и при s = 0,5 – симметричную схему (14). Исследуем погрешность аппроксимации схемы (15) на решении исходной задачи (1) – (3). Представим решение задачи (15) в виде y i n = u(x i , t n ) + z i n , где u(x i , t n ) – точное решение дифференциальной задачи (1) – (3). Тогда для погрешности получим систему уравнений

(16)

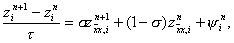
i = 1, 2,…, N – 1, n = 0, 1,…, K – 1,

z 0 n+1 = z N n+1 = 0, n = 0, 1,…, K – 1, z i 0 = 0, i = 0, 1,…, N.

Сеточная функция y i n , входящая в правую часть уравнения (16) и равная

(17)

называется погрешностью аппроксимации схемы (15) на решении задачи (1) – (3). Получим первые члены разложения функции y i n по степеням h и t . Будем разлагать все функции, входящие в выражение для y i n , по формуле Тейлора в точке (x i , t n + 0,5 t ). Учитывая разложения

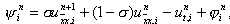
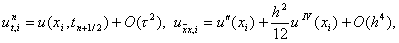
Отсюда, проводя разложение в точке (x i , t n+1/2 ) и обозначая u = u (x i , t n+1/2 ) , будем иметь

и, перегруппировывая слагаемые, получим, что

Учитывая уравнение (1) u’’ – u = – f и следствие из него u IV – u’’ = –f’’ , окончательно можно записать, что

(18)

Из формулы (18) можно сделать следующие выводы. Если

то схема (15) имеет второй порядок аппроксимации по t и четвертый – по h . Такая схема называется схемой повышенного порядка аппроксимации. Если

то схема (15) имеет второй порядок аппроксимации по t и по h. При остальных значениях s и при j i n º 0 в виде (10), то получим

и |q| £ 1 при всех j , если

(19)

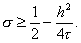
Отсюда видно, в частности, что все схемы с s ³ 0,5 абсолютно устойчивы. Схема повышенного порядка аппроксимации ( s = s * ) также абсолютно устойчива, что проверяется непосредственно.

При s ¹ 0 разностная схема (15) является неявной схемой. Для нахождения решения y i n+1 по заданным y i n требуется решать систему уравнений

(20)

где

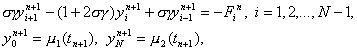
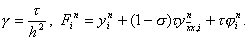
Система (20) решается методом прогонки. Условия устойчивости прогонки при s ¹ 0 сводятся к неравенству

|1 + 2 s g | ³ 2 | s | g

и выполнены при s ³ – 1/(4 g ). Последнее неравенство следует из условия устойчивости (19) разностной схемы.

3.4. Уравнения с переменными коэффициентами и линейные уравнения.

Рассмотрим первую краевую задачу для уравнения теплопроводности с переменными коэффициентами

(21)

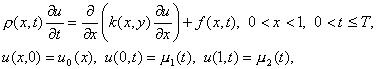
где r (x, t), k(x, t), f(x, t) – достаточно гладкие функции, удовлетворяющие условиям

0 1 £ k(x, t) £ c 2 , r (x, t) ³ c 3 > 0 .(22)

Дифференциальное выражениепри каждом

фиксированном t аппроксимируем в точке (x i , t) так же, как и в стационарном случае, разностным отношением

где разностный коэффициент теплопроводности a(x i , t) должен удовлетворять условиям второго порядка аппроксимации

Наиболее употребительны следующие выражения для a(x i , t) :

Разностная схема с весами для задачи (21) имеет вид

(24)

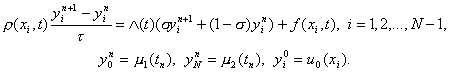
Здесь в качестве t можно взять любое значение t Î [t n , t n+1 ] , например t = t n + 0,5 t . Если в уравнении (24) t = t n + 0,5 t , s = 0,5 , то схема (24) имеет второй порядок аппроксимации по t и по h . При остальных значениях s и t выполняется первый порядок аппроксимации по t и второй – по h .

При исследовании устойчивости разностных схем с переменными коэффициентами иногда применяется принцип замороженных коэффициентов, сводящий задачу к уравнению с постоянными коэффициентами. Рассмотрим явную схему, соответствующую уравнению (24) с s = 0 и f(x i , t) º 0 , т.е. схему

(25)

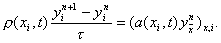
Предположим, что коэффициенты r (x i , t), a(x i , t) – постоянные, r (x i , t) º r = const, a(x i , t) º a = const . Тогда уравнение (25) можно записать в виде

или

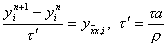
Из п.2 известно, что последнее уравнение устойчиво при t ’ £ 0,5h 2 , т.е. при

(26)

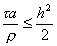
Принцип замороженных коэффициентов утверждает, что схема (25) устойчива, если условие (26) выполнено при всех допустимых значениях a(x i , t), r (x i , t) , т.е. если при всех x, t выполнены неравенства

(27)

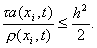
Если известно, что 0 1 £ a(x i , t) £ c 2 , r (x i , t) ³ c 3 > 0 , то неравенство (27) будет выполнено при

Строгое обоснование устойчивости схемы (25) будет дано в примере 2 из главы 2.

Если параметр s ³ 0,5, то из принципа замороженных коэффициентов следует абсолютная устойчивость схемы (24).

Рассмотрим теперь первую краевую задачу для нелинейного уравнения теплопроводности

(28)

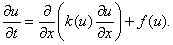
В случае нелинейных уравнений, когда заранее неизвестны пределы изменения функции k(u) , избегают пользоваться явными схемами. Чисто неявная схема, линейная относительно y i n+2 , i = 1, 2,…, N – 1 , имеет вид

(29)

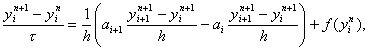
где a i = 0,5 (k(y n i ) + k(y n i-1 )) . Эта схема абсолютно устойчива, имеет первый порядок аппроксимации по t и второй – по h . Решение y i n+1 , i = 1, 2,…, N – 1 , находится методом прогонки. Заметим, что схему (29) можно записать в виде

где k i = k(y i n ) .

Часто используется нелинейная схема

(30)

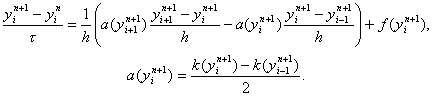
Для реализации этой схемы необходимо применить тот или иной итерационный метод. Например такой:

(31)

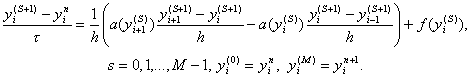
Здесь s – номер итерации. Как видим, нелинейные коэффициенты берутся с предыдущей итерации, а в качестве начального приближения для y i n+1 выбирается y i n . Это начальное приближение тем лучше, чем меньше шаг t . Число итераций M задается из соображений точности. В задачах с гладкими коэффициентами при k(u) ³ c 1 > 0 часто бывает достаточно провести две – три итерации. Значения y i (S+1) на новой итерации находятся из системы (31) методом прогонки. При M = 1 итерационный метод (31) совпадает с разностной схемой (29).

Для приближенного решения нелинейного уравнения (28) применяются также схемы предиктор – корректор второго порядка точности, аналогичные методу Рунге – Кутта для обыкновенных дифференциальных уравнений. Здесь переход со слоя n на слой n+1 осуществляется в два этапа. Приведем пример такой схемы. На первом этапе решается неявная линейная система уравнений

из которой находятся промежуточные значения y i n+1/2 , i = 0, 1,…, N . Затем на втором этапе используется симметричная шеститочечная схема для уравнения (28), в которой нелинейные коэффициенты a(y), f(y) вычисляются при y = y i n+1/2 , т.е. схема

Опорный конспект лекции

Ф СО ПГУ 7.18.2/06

Министерство образования и науки Республики Казахстан

Павлодарский государственный университет им. С. Торайгырова

дисциплины «Численные методы решения задач математической физики»

для специальности 050601 Математика

Ф СО ПГУ 7.18.1/07

УТВЕРЖДАЮ

Проректор по УР

Составители: доцент ,

преподаватель

Кафедра «Информатика и информационные системы»

Опорный конспект лекции

по дисциплине «Численные методы решения задач математической физики »

для студентов специальностей 050601 Математика

Рекомендована на заседании кафедры от “____”___200___г.

Заведующая кафедрой ___________

Одобрена методическим советом факультета Физики, математики и информационных технологий “___”______200 _ г. Протокол №___

Председатель МС__________________________

Тема 1. Основные задачи математической физики.

Разностные уравнения. Пространство сеточных функций. Разностные операторы. Разностная аппроксимация оператора Лапласа. Задачи на собственные значения для разностного оператора Лапласа. Разностные формулы Грина. Свойства разностных операторов. Априорные оценки. Аппроксимация дифференциальной начально-краевой задачи разностной схемой. Шаблон. Порядок аппроксимации. Определение устойчивости. Аппроксимация нормированного пространства. Внутренние и внешние аппроксимации. Невязка. Ошибка аппроксимации. Устойчивость. Сходимость.

Решение обыкновенных дифференциальных уравнений зависит лишь от одной переменной и так далее. Во многих практических задачах решения — искомые функции зависят от нескольких переменных и уравнения, описывающие данные задачи могут содержать частные производные искомых функции. Они называются уравнениями с частными производными.

Математическая постановка задачи вместе с дифференциальными уравнениями содержит и некоторые дополнительные условия. Если решение ищется в ограниченной области, то задаются условия на ее границе, называемые граничными (краевыми) условиями. Такие задачи носят названия краевых задач для уравнений с частными производными.

Задача, которая состоит в решении уравнений при заданных начальных условиях, называется задачей Коши (ЗК) для уравнений с частными производными. При этом задача решается в неограниченном пространстве , и граничные условия не задаются. Задача, у которой ставится , и начальные и граничные условия называются нестационарными (смешанными) краевыми задачами. Получающиеся при этом решения меняются с течением времени.

Задачи, решение которых существует и единственно в некотором классе начальных и граничных условий и непрерывно зависит как от этих условий, так и от коэффициентов этих уравнений, называются корректно поставленными.

Среди численных методов рассмотрим разностные методы, которые основаны на введение некоторой разностной сетки в рассматриваемой области. Все значения производных, начальные и граничные условия выражаются через значения функции в узлах сетки, в результате чего получается система линейных уравнений, называемая разностной схемой. Построение разностных схем решения уравнений с частными производными основано на введение сетки в рассматриваемой области. Узлы сетки являются расчетными точками.

a £ x £ b xi = a + ih 1 ( I =0,1,…, I )

c £ y £ d yj=c+jh2 (j=0,1,…,J)

Для построения разностной схемы, частные производные в уравнений заменяются, конечно — разностными соотношениями по некоторому шаблону. При этом точные значения искомой функции U заменяются значениями сеточной функции u в узлах разностной сетки.

Разностная схема для решения уравнения теплопроводности при заданных начальных и граничных условий имеет следующий вид:

— распределение температуры на концах рассматриваемого отрезка [0,1] в любой момент, начальные и граничные условия должны быть согласованы, то есть . Вводим прямоугольную сетку:

— шаги. — значение функции в узлах сетки. Таким образом,

Получаем систему алгебраических уравнений для определения значений сеточных функции во внутренних узлах. Из граничного условия

(4)

При совокупность узлов называется слоем. Из (2) находим последовательно значения на слое через соответствующие значения на — том слое. Такие схемы называются явными. Для начала счета при необходимо решение на начальном слое, которое определяется начальным условием, имеющим следующий вид:

(5)

В отличие от явной схемы каждое разностное уравнение (3) содержит на каждом новом слое значения неизвестных в трех точках, поэтому нельзя сразу определить эти значения через известное решение на предыдущем слое. Они носят названия неявных схем. При этом разностная схема (3) состоит из линейных трехточечных уравнений, то есть каждое уравнение содержит неизвестную функцию в трех точках данного слоя. Решаются методом прогонки.

В данном примере рассматривали двухслойную схему, т. е. в каждое разностное уравнение входят значения функции их двух слоев – нижнего, на котором решение уже найдено, и верхнего, в узлах которого решение ищется.

Сходимость. Аппроксимация. Устойчивость .

Дифференциальная задача состоит в решение уравнения с частными производными при заданных начальных и граничных условии записывается в операторном виде:

(6)

Операторное уравнение включает исходное уравнение с частными производными, и дополненное, включающее начальные и граничные условия. описывает правые части уравнения, начальные и граничные условия, включает и расчетную область, и границу. Дифференциальную задачу (6) заменяем разностной задачей, где , где .

(7)

Значение сеточной функции в узлах сетки приближенно заменяют значения искомой функции в тех же узлах с погрешностями

. (8)

Вводим .

Разностная схема (7) называется сходящейся, если при сгущении узлов сетки, это значение погрешности стремится к нулю, т. е. если (9).

Если где , то разностная схема имеет k-ый порядок точности или говорят, что она сходится со скоростью .

Запишем уравнение (7) для погрешности решения на сетке . Подставляя в (7), имеем (10)

Величина называется невязкой (погрешностью аппроксимации) разностной схемы. Вводим характеристическую величину

(11)

при аппроксимация имеет k — ый порядок относительно h. Разностная схема (7) аппроксимирует исходную дифференциальную задачу (6), если при измельчении сетки невязка стремится к нулю, т. е. если

(1 2 )

Абсолютной (безусловной) аппроксимацией называется аппроксимация такого типа, когда невязка стремится к нулю при по любому закону без каких — либо условий. При условной аппроксимации налагаются некоторые условия на размеры шагов по пространству и времени. Разностная схема (7) называется устойчивой, если ее решение непрерывно зависит от входных данных, т. е. малому изменению входных данных соответствует малое изменение решения. Устойчивость характеризует чувствительность разностной схемы к различного рода погрешностям.

Теорема: Если решение исходной дифференциональной задачи (6) существует, а разностная схема (7) устойчива и аппроксимирует (6) на данном решение, то разностное решение сходится к точному.

[1] — [5], введение, глава 5

Тема 2. Разностные схемы для уравнений параболического типа

Классы устойчивых двухслойных схем. Энергетическое тождество. Дискретизация одномерного уравнения теплопроводности. Шаблоны. Порядок разностной аппроксимации. Исследование устойчивости методом Фурье. Начально-краевые задачи. Семейство шеститочечных схем. Явная и неявная схемы. Схема Кранка-Николсона. Порядок аппроксимации, устойчивость. Трехслойные схемы для уравнения теплопроводности. Схема Дюфорта и Франкеля. Порядок аппроксимации и устойчивости. Схема «ромб». Погрешности аппроксимации, устойчивости. Схемы с весами. Погрешность аппроксимации и устойчивость.

2.1 Постановка задач для уравнений параболического типа

Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). В одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид

. ( 2 .1)

Если на границах х=0 и х=l заданы значения искомой функции u(x, t) в виде

( 2 .2)

т. е. граничные условия первого рода, и, кроме того, заданы начальные условия

то задачу (2.1)-(2.4) называют первой начально-краевой задачей для уравнения теплопроводности (2.1).

В терминах теории теплообмена u(x, t) – распределение температуры в пространственно-временной области коэффициент температуропроводности, а (2.2), (2.3) с помощью функций ϕ 0 (t), ϕ l (t) задают температуру на границах x=0 и x=l.

Если на границах х=0 и х=l заданы значения производных искомой функции по пространственной переменной

(2.5) (2.6)

т. е. граничные условия второго рода, то задачу (25.1), (2.5), (2.6), (2.4) называют второй начально-краевой задачей для уравнения теплопроводности (2.1). В терминах теории теплообмена на границах в этом случае заданы тепловые потоки.

Если на границах заданы линейные комбинации искомой функции и ее производной по пространственной переменной

(2.7)

(2.8)

т. е. граничные условия третьего рода, то задачу (2.1), (2.7), (2.8), (2.4) называют третьей начально-краевой задачей для уравнения теплопроводности (2.1). В терминах теории теплообмена граничные условия (2.7), (2.8) задают теплообмен между газообразной или жидкой средой и границами расчетной области с неизвестными температурами u(0,t), u(l, t).

Для пространственных задач теплопроводности в области первая начально-краевая задача имеет вид

Аналогично ставится вторая и третья начально-краевые задачи для пространственного уравнения задачи (2.9) – (2.11).

На практике часто ставятся начально-краевые задачи теплопроводности со смешанными краевыми условиями, когда на границах задаются граничные условия различных родов.

2 .1.2. Понятие о методе конечных разностей. Применение метода конечных разностей к решению уравнений параболического типа

Основные определения, связанные с методом конечных разностей, рассмотрим на примере конечно-разностного решения первой начально-краевой задачи для уравнения теплопроводности (2.1)-(2.4). Нанесем на пространственно-временную область 0≤x≤l, 0≤t≤T конечно-разностную сетку ω hτ

(2.12)

с пространственным шагом h=l/N и шагом по времени τ=T/K (рис 2.1).

Введем два временных слоя: нижний tk=kτ , на котором распределение искомой функции u(xj, tk), известно (при k=0 распределение определяется начальным условием (2.4) u(xj, t0)=ψ(xj)) и верхний временной слой tk+1=(k+1)τ, на котором распределение искомой функции u(x j j ,tk+1), j =0,1,…,N подлежит определению.

Рис. 2 .1. Конечно-разностная сетка

Сеточной функцией задачи (2.1)-(2.4) (обозначение ) назовем однозначное отображение целых аргументов j, k в значения функции

На введенной сетке (2.12) введем сеточные функции первая из которых известна, вторая – подлежит определению. Для ее определения в задаче (2.1)-(2.4) заменим (аппроксимируем) дифференциальные операторы отношением конечных разностей (см. раздел «Численное дифференцирование»), получим

(2.13)

(2.14)

Подставляя (2.13), (2.14) в задачу (2.1)-(2.4), получим явную конечно-разностную схему для этой задачи в форме

(2.15)

где для каждого j -го уравнения все значения сеточной функции известны, за исключением одного , которое может быть определено явно из соотношений (2.15). В соотношения (2.15) краевые условия ( j =0, j = N ) входят при значениях j=1 и j=N-1, а начальное условие – при k=0.

Если в (2.14) дифференциальный оператор по пространственной переменной аппроксимировать отношением конечных разностей на верхнем временном слое

(2.16)

то после подстановки (2.13), (2.16) в задачу (2.1)-(2.4), получим неявную конечно-разностную схему для этой задачи

( 2 .17)

Теперь сеточную функцию на верхнем временном слое можно получить из решения СЛАУ (2.17) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид

Шаблоном конечно-разностной схемы называют ее геометрическую интерпретацию на конечно-разностной сетке.

Рис. 2 .2. Шаблоны явной и неявной конечно-разностных схем для уравнения теплопроводности

На рисунке 2.2 приведены шаблоны для явной (2.15) и неявной (2.17) конечно-разностных схем при аппроксимации задачи (2.1)-(2.4).

Явная конечно-разностная схема (2.15), записанная в форме

(2.18)

обладает тем достоинством, что решение на верхнем временном слое получается сразу (без решения СЛАУ) по значениям сеточных функций на нижнем временном слое , где решение известно (при k=0 значения сеточной функции формируются из начального условия (2.4.)). Но эта же схема обладает существенным недостатком, поскольку она является условно устойчивой с условием , накладываем на сеточные характеристики τ и h.

С другой стороны, неявная конечно-разностная схема (2.17), записанная форме

( 2 .19)

приводит к необходимости решать СЛАУ, но зато эта схема абсолютно устойчива.

Проанализируем схемы (2.18), (2.19). Пусть точное решение, которое не известно, возрастает по времени, т. е. . Тогда, в соответствии с явной схемой (2.18) разностное решение будет заниженным по сравнению с точным, т. к. определяется по меньшим значениям сеточной функции на предыдущем временном слое, поскольку решение является возрастающим по времени.

Для неявной схемы (2.19) на возрастающем решении, наоборот, решение завышено по сравнению с точным, поскольку оно определяется по значениям сеточной функции на верхнем временном слое.

На убывающем решении картина изменяется противоположным образом: явная конечно-разностная схема завышает решения, а неявная — занижает (см. рис. 2.3)

Рис. 2 .3. Двусторонний метод аппроксимации

На основе этого анализа возникла идея о построении более точной неявно-явной конечно-разностной схемы с весами при пространственных конечно-разностных операторах, причем при измельчении шагов τ и h точное (неизвестное) решение может быть взято в ″вилку″ сколь угодно узкую, т. к. если явная и неявная схемы аппроксимируют дифференциальную задачу и эти схемы устойчивы, то при стремлении сеточных характеристик и h к нулю, решения по явной и неявной схемам стремятся к точному решению с разных сторон.

Рассмотрим неявно-явную схему с весами для простейшего уравнения теплопроводности

( 2 .20)

где θ — вес неявной части конечно-разностной схемы, 1−θ — вес для явной части, причем 0≤θ≤1. При θ=1 имеем полностью неявную схему, при θ=0 — полностью явную схему, и при θ=1/2 — схему Кранка-Николсона. Для схемы Кранка-Николсона (θ=1/2) порядок аппроксимации составляет, т. е. на один порядок по времени выше, чем обычные явная или неявная схемы.

Неявно-явная схема с весами (2.20) абсолютно устойчива при 1/2≤θ≤1 и условно устойчива с условием при 0≤θ

Таким образом, схема Кранка-Николсона (2.20) при θ=1/2 абсолютно устойчива и имеет второй порядок аппроксимации по времени и пространственной переменной x.

2 .1.3. Аппроксимация граничных условий, содержащих производные

В задачах математической физики вообще, и в задачах теплопроводности в частности, граничные условия 1-го рода аппроксимируются точно в узлах на границе расчетной области. Граничные условия 2-го и 3-го рода отличаются тем, что в них присутствует производная первого порядка искомой функции по пространственной переменной. Поэтому для замыкания конечно-разностной схемы необходима их аппроксимация. Простейшим вариантом является аппроксимация производных направленными разностями первого порядка:

Тогда в общем случае граничных условий 3-го рода (2.7), (2.8) уравнения, связывающие значения искомой функции в двух крайних узлах разностной сетки, выглядят следующим образом:

Дополняя полученными уравнениями явную конечно-разностную аппроксимацию во внутренних узлах, получим явную разностную схему для третьей начально-краевой задачи (2.1), (2.4), (2.7), (2.8).

В результате алгоритм перехода на новый временной слой с использованием явной схемы можно представить в следующем виде:

Т. е. сначала рассчитываются значения искомой функции во всех внутренних узлах на новом временном слое, а затем определяются значения на границах.

При использовании неявной конечно-разностной схемы получаем следующий разностный аналог дифференциальной задачи:

В результате для получения решения на новом временном слое решается система линейных алгебраических уравнений с трехдиагональной матрицей. Аналогичная картина имеет место и при использовании неявно-явной схемы с весами.

Принципиальной особенностью рассмотренного выше подхода является первый порядок аппроксимации граничных условий. Т. е. порядок аппроксимации в граничных узлах ниже порядка аппроксимации во внутренних узлах расчетной области. При этом глобальный порядок аппроксимации (во всей расчетной области) равен наименьшему относительно всех узлов сетки порядку аппроксимации.

Одним из способов повышения порядка аппроксимации граничных условий является использование формул численного дифференцирования второго порядка:

В случае явной схемы алгоритм вычисления решения на новом временном слое при такой аппроксимации граничных условий не приобретает принципиальных изменений. Если же используется неявная схема, то получающаяся при этом СЛАУ теряет трехдиагональный вид (первое и последнее уравнение содержат три неизвестных). Этот недостаток легко устраним, т. к. путем линейной комбинации первого уравнения со вторым (последнего с предпоследним) можно добиться исключения третьего неизвестного из соответствующего уравнения. Однако при этом возможно нарушение диагонального преобладания матрицы и, следовательно, нарушение условий применимости метода прогонки.

Более эффективным является подход, позволяющий повысить порядок аппроксимации граничных условий без увеличения числа узлов в аппроксимационных соотношениях. Для иллюстрации этого подхода рассмотрим следующий пример.

Решить третью начально-краевую задачу для параболического уравнения, содержащего как конвективные члены (пропорциональные производной ), так и источниковые члены, содержащие искомую функцию

(2.21)-(2.24) Решение.

Во внутренних узлах конечно-разностной сетки неявная конечно-разностная схема для уравнения (2.21) имеет вид:

(2.25)

Если производные первого порядка в граничных условиях (2.22) и (2.23) аппроксимировать по следующей схеме (с помощью отношения конечных разностей справа и слева)

то граничные условия аппроксимируются с первым порядком, и глобальный порядок будет равен первому порядку несмотря на то, что во всех остальных узлах порядок аппроксимации по пространственным переменным равен двум. Для сохранения порядка аппроксимации, равного двум, в граничных узлах разложим на точном решении значение в окрестности точки x=0 в ряд Тейлора по переменной x до третьей производной включительно, — в аналогичный ряд в окрестности точки x= l , получим (в предположении что функция u(x, t) в граничных узлах имеет первые производные по времени и вторые — по x):

(2.26)

. (2.27)

Далее, подставим сюда значения второй производной в граничных узлах, полученные из дифференциального уравнения (2.21):

и найдем из полученных выражений (2.26), (2.27) значения первой производной в граничных узлах с порядком

Подставляя в (2.22), а в (2.23) и аппроксимируя полученные соотношения в соответствующих граничных узлах (при этом получим алгебраические уравнения для граничных узлов, в каждом из которых два неизвестных:

(2.28)

(2.29)

Таким образом, (2.28) — конечно-разностная аппроксимация граничного условия 3-го рода (2.22) на левой границе x=0, а (2.29) — конечно-разностная аппроксимация граничного условия 3-го рода (2.23) на правой границе x=l, которые сохраняют тот же порядок аппроксимации, что и в конечно-разностной аппроксимации (2.25) дифференциального уравнения (2.21).

Приписывая к граничным конечно-разностным уравнениям (2.28), (2.29), каждое из которых содержит два значения сеточной функции, алгебраические уравнения (2.25), записанные в виде

(2.30)

получим СЛАУ с трехдиагональной матрицей, решаемую методом прогонки

(2.31)

Изложенный метод аппроксимации краевых условий, содержащих производные по пространственным переменным, повышает не только порядок аппроксимации, но и сохраняет консервативность конечно-разностной схемы, т. е. в конечно-разностной аппроксимации соблюдаются законы сохранения, на основе которых выведены дифференциальные соотношения задачи (2.

Аналогичный подход можно осуществить в краевых задачах для дифференциальных уравнений любых типов.

Тема 3. Разностные схемы для уравнений гиперболического типа Разностные схемы для уравнения колебания струны. Явная схема («крест»). Неявная схема (типа Кранка-Николсона). Порядок аппроксимации. Исследование устойчивости методом Фурье. Семейство схем с весами. Устойчивость. Погрешность аппроксимации. Исследование устойчивости разностных схем для уравнения колебания.

3.1. Постановка задач для уравнений гиперболического типа

Классическим примером уравнения гиперболического типа является волновое уравнение, которое в области 0 0 имеет вид:

Данное уравнение описывает, в частности, процесс малых поперечных колебаний струны. В этом случае u(x, t) — поперечные перемещения (колебания) струны, а – скорость распространения малых возмущений в материале, из которого изготовлена струна.

Если концы струны движутся по заданным законам, то есть на концах заданы перемещения (или значения искомой функции), то первая начально-краевая задача для волнового уравнения имеет вид:

(3.

причем, если концы струны жестко закреплены, то ϕ 0 (t)= ϕ l (t)=0.

Как видно, в задачах для волнового уравнения, кроме начального распределения искомой функции, задается еще распределение начальной скорости перемещения.

Если на концах струны заданы значения силы, которая по закону Гука пропорциональна значениям производной перемещения по пространственной переменной (то есть на концах заданы значения первых производных по переменной x), то ставится вторая начально-краевая задача для волнового уравнения:

В условиях, когда концы струны свободны, функции ϕ 0 (t)= ϕ l (t)=0.

Наконец в условиях, когда концы закреплены упруго, т. е. на концевые заделки действуют силы, пропорциональные перемещениям, ставится третья начально-краевая задача для волнового уравнения:

Аналогично ставятся двумерные и трехмерные начально-краевые задачи для двумерного и трехмерного волнового уравнения.

3.2 Конечно-разностная аппроксимация уравнений гиперболического типа

Рассмотрим первую начально-краевую задачу для волнового уравнения (3.1)-(3.5). На пространственно-временной сетке (3.12) будем аппроксимировать дифференциальное уравнение (3.1) одной из следующих конечно-разностных схем:

(3.6) с шаблоном на рисунке 3.1а и

(3. 7 )

Рис. 3.1. Шаблоны конечно-разностных схем для волнового уравнения

с шаблоном на рисунке 3.1 б

При этом схема (3.6) является явной. С ее помощью решение определяется сразу, поскольку значения сеточных функции, на нижних временных слоях должны быть известны. В соответствии с шаблоном для этой схемы порядок аппроксимации равен двум, как по пространственной, так и по временной переменной. При этом явная конечно-разностная схема (3.6) для волнового уравнения условно устойчива с условием , накладываемым на сеточные характеристики τ , h ..

Схема (3.7) является неявной схемой и обладает абсолютной устойчивостью. Ее можно свести к СЛАУ с трехдиагональной матрицей, решаемой методом прогонки.

В обеих схемах необходимо знать значения на нижних временных слоях. Для k =1 это делается следующим образом:

(3.8)

где функция из начального условия (3.5).

Для определения можно воспользоваться простейшей аппроксимацией второго начального условия (3.6):

Откуда для искомых значений получаем следующее выражение:

Недостатком такого подхода является первый порядок аппроксимации второго начального условия. Для повышения порядка аппроксимации воспользуемся следующей процедурой.

Разложим в ряд Тейлора на точном решении по времени в окрестности t=0 :

. (3.9)

Для определения второй производной в выражении (3.9) воспользуемся исходным дифференциальным уравнением.

В результате получаем искомую сеточную функцию со вторым порядком точности:

. После определения из начальных условий значений сеточных функций, на двух первых временных слоях вычислительный процесс продолжается согласно схемам (3.8) или (3.9). При этом аппроксимация краевых условий (3.3) и (3.4) производится аналогично тому, как это описывалось выше для уравнений параболического типа. Для иллюстрации этого этапа рассмотрим следующий пример.

Выписать явную конечно-разностную схему для третьей начально-краевой задачи.

Аппроксимация дифференциального уравнения на шаблоне (3.1б) выглядит следующим образом:

где.

Граничные условия аппроксимируем с первым порядком:

. В результате переход на новый временной слой представляется следующим алгоритмом:

Таким образом, сначала рассчитываются значения искомой функции u во внутренних узлах на новом временном слое, после чего из аппроксимации граничных условий находятся значения функции в крайних узлах.

Для окончательного замыкания вычислительного процесса определим, исходя из начальных условий, значения искомой функции на двух первых временных слоях

В начальный момент времени значения определяются точно:

. Если воспользоваться аппроксимацией первого порядка по времени, то как было показано выше, получим

. Для повышения порядка аппроксимации разложим в ряд Тейлора на точном решении по времени в окрестности t=0 :

где, согласно исходному уравнению

Окончательно получаем .

Тема 4. Разностные схемы для уравнений эллиптического типа Задача Дирихле для уравнения Пуассона в квадрате. Аппроксимация. Однозначная разрешимость. Принцип максимума. Устойчивость. Разностная задача Дирихле в прямоугольнике. Сложная область. Связные и несвязные области. Метод установления. Явная и неявная схемы. Схема переменных направлений. Анализ явной схемы установления и анализ схемы переменных направлений.

Классическим примером уравнения эллиптического типа является уравнение Пуассона

или уравнение Лапласа при f(x, y)≡0.

Здесь функция u(x, y) имеет различный физический смысл, а именно: стационарное, независящее от времени, распределение температуры, скорость потенциального (безвихревого) течения идеальной (без трения и теплопроводности) жидкости, распределение напряженностей электрического и магнитного полей, потенциала в силовом поле тяготения и т. п.

Если на границе Г расчетной области задана искомая функция, то соответствующая первая краевая задача для уравнения Лапласа или Пуассона называется задачей Дирихле

(4.1)-(4.2)

Если на границе Г задается нормальная производная искомой функции, то соответствующая вторая краевая задача называется задачей Неймана для уравнения Лапласа или Пуассона

(4.3)-(4.4)

При этом n – направление внешней к границе Г нормали.

Более приемлемой является координатная форма краевого условия (4.4)

где − направляющие косинусы внешнего вектора единичной нормали к границе Г, i и j орты базисных векторов.

Наконец третья краевая задача для уравнения Пуассона (Лапласа) имеет вид

4.1. Конечно-разностная аппроксимация задач для уравнений эллиптического типа

Рис. 4.1. Центрально-симметричный шаблон

Рассмотрим краевую задачу для уравнений Лапласа или Пуассона (4.1), (4.2) в прямоугольнике , на который наложим сетку

(4.5)

На этой сетке аппроксимируем дифференциальную задачу во внутренних узлах с помощью отношения конечных разностей по следующей схеме (вводится сеточная функция ):

(4.6)

которая на шаблоне имеет второй порядок по переменным и, поскольку шаблон центрально симметричен.

СЛАУ имеет пяти-диагональный вид (каждое уравнение содержит пять неизвестных и при соответствующей нумерации переменных матрица имеет ленточную структуру). Решать ее можно различными методами линейной алгебры, например, итерационными методами, методом матричной прогонки и т. п.

Рис.4.2 Центрально — симметричный шаблон

Рассмотрим разностно-итерационный метод Либмана численного решения задачи Дирихле (4.1), (4.2). Для простоты изложения этого метода примем, тогда из схемы (4.6 ) получим (k-номер итерации)

(4.8)

На каждой координатной линии (например, ) с помощью линейной интерполяции (см. рис.4.3) граничных значений определим на нулевой итерации, подставив которые в (4.8), получим распределение на первой итерации

Рис. 4.3. К разностно-итерационному методу Либмана

Это распределение снова подставляются в (4.8), получаем распределение и т. д. Процесс Либмана прекращается, когда ,

где — наперед заданная точность.

При решении задач с граничными условиями 2-го и 3-го родов наряду с аппроксимацией дифференциального уравнения производится также аппроксимация граничных условий. Здесь в качестве примера приведем разностную схему, аппроксимирующую третью краевую задачу для уравнения Пуассона в прямоугольнике.

Как и ранее в прямоугольнике построим сетку

На этой сетке аппроксимируем дифференциальную задачу во внутренних узлах по рассмотренной выше центрально-разностной схеме

. Граничные условия аппроксимируем с первым порядком с помощью направленных разностей:

. В результате получена СЛАУ, содержащая уравнений ( N 1 +1)( N 2 +1)-4 относительно неизвестных ( i =0,1,…, N 1 , j =0,1,…, N 2 ) при этом угловые узлы с координатами ( i , j ), равными в вычислениях не участвуют). Как и в случае граничных условий первого рода, она имеет пятидиагональный вид и может быть решена, например, итерационным методом Либмана.

Замечание. Метод простых итераций для решения СЛАУ, возникающих при аппроксимации уравнения Пуассона (Лапласа), отличается довольно медленной сходимостью. Этот недостаток может стать существенным при использовании мелких сеток, когда число уравнений в системе становится большим.

Тема 5. Вариационные и вариационно-разностные методы Метод Ритца. Описание метода Ритца. Формулировка метода и применение для решения разностной задачи Дирихле. Построение простейших разностных уравнений диффузии с помощью метода Ритца.

Глава 4, §4.1, §4.2, §4.3, §4.4 , Уравнения математической физики, М.: Физматлит, 2003.

Тема 6. Численные методы решения интегральных уравнений Метод конечных сумм для решения интегральных уравнений Фредгольма и Вольтерра. Метод вырожденных ядер. Резольвента. Нахождение собственных значений и собственных функций. Метод наименьших квадратов. Методы Монте-Карло.

. Численные методы Монте-Карло. М.: Наука, 1973.

. Метод Монте-Карло. М.: Наука, 1985.

5. Список литературы

1 .Калиткин методы. М.: Наука, 1978.

2. , , Шувалова методы анализа. М.: Наука, 1967.

3. Бахвалов методы. Том 1, изд. 2-е, стереотипное, М.,1975.

4. Ермаков СМ., Михайлов моделирование. Изд. 2-е. М.: Наука, 1982.

5. . Численные методы Монте-Карло. М.: Наука, 1973.

6. . Метод Монте-Карло. М.: Наука, 1985.

7. Самарский разностных схем. М.: Наука, 1977.

8. Марчук вычислительной математики. М.:Наука, 1989.

9. Бабенко численного анализа. М.: Наука. 1986.

10. , , Монастырный методы. Т. 1. М.: Наука, 1976, Т. 2. М.: Наука, 1977.

11., Гулин методы. М.: Наука, 1989.

12., Рябенький B . C . Разностные схемы, введение в теорию. М: Наука, 1977.

13. Васильев Ф .П. Численные методы решения экстремальных задач. – М., 1980 – 520 с. с илл.

14. Кириллова максимума в теории оптимального управления. – Минск: Наука и техника, 1974.

15. Гамкрелидзе оптимального управления. – Тбилиси: Изд-во Тбилисского ун-та, 1977

1.Шакенов Монте-Карло и их приложения. Алматы: КазГУ,1993.

2. , , Ривин по вычислительной математике. М.: Наука, 1980.

3., , Вычислительная математика в примерах и задачах. М.: Наука, 1972.

4.Черкасова задач по численным методам. Минск: Высшая школа, 1967.

5.ВазовВ., Дж. Форсайт. Разностные методы решения дифференциальных

уравнений в частных производных. М.: ИЛ, 1963.

6.Ортега Дж., Итерационные методы решения нелинейных

систем уравнений со многими неизвестными. М.: Наука, 1975.

7. Метод конечных элементов для уравнений с частными производными. М.: Мир, 1981.

8.Трауб Дж. Итерационные методы решения уравнений. М.: Мир, 1983.

9.Михлин вопросы теории погрешностей. Л.: ЛГУ, 1988.

10.Михлин методы в математической физике. М., 1970.