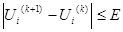Итерационные методы решения систем уравнений установившегося режима
Общая характеристика методов
Методы решения систем уравнений — прямые (точные) и итерационные (приближенные). Прямые применяются для решения систем линейных урав-нений, итерационные — для решения систем линейных и нелинейных уравне-ний.
Нелинейные уравнения установившегося режима формируются, если в узлах сети задана постоянная мощность(нагрузка или генерация).
Суть итерационных методов: задается некоторое начальное прибли-жение неизвестных U (0) , которое постепенно уточняется в ходе выполнения ряда однотипных шагов вычислений (итераций). Если итерационный про-цесс сходится, то получаем искомое решение U (*) с заданной точностью.
Итерациями называются многократно повторяющиеся однотипные ша-ги вычислений.
Основные характеристики итерационных методов:
1. Условия сходимости к решению, при которых происходит приближе-ние к искомому решению U (*) , либо удаление от него;
2. Скорость сходимости. Характеризуется количеством итераций n, необ-ходимых для достижения решения с заданной точностью, или законом изменения вектора погрешности при переходе от итерации к итерации;
2.3. 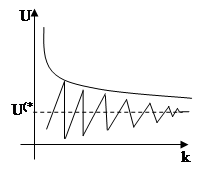
Возможно влияние на скорость сходимос-ти за счет введения дополнительных коэффици-ентов;
4. Необходимость хранения в памяти ЭВМ всех коэффициентов систем уравнений. Удобство программирования, простота алгоритмов и т.д.
Рассматриваем систему нелинейных уравнений установившегося режи-ма. В матричной форме она имеет вид:
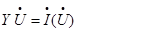
В развернутой форме такая система уравнений может быть представлена в следующем виде:

Преобразуем систему (2) квиду, пригодному для решения ее итераци-онными методами. Для этого каждое уравнение системы решим относитель-но одной из неизвестных величин Ui:
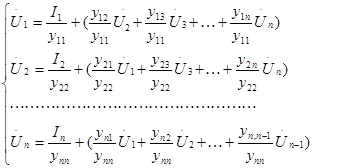
Любое i-ое уравнение этой системы можно записать в общем виде:
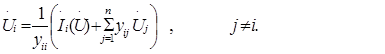
Если задать начальные приближения неизвестных U (0) , подставить их в правую часть уравнений (4) и выполнить необходимые вычисления, опреде-лим следующее приближение неизвестных U (1) и т.д. Такая после-довательность действий соответствует методу простой итерации. Тогда (4) в итерационной форме:
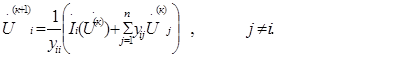
В матричной форме система (3) может быть записана следующим образом:
здесь 
D — вектор свободных членов, 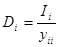
С — матрица коэффициентов при неизвестных, 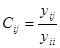
В итерационном виде система (5) принимает вид:
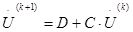
Здесь к – номер приближения неизвестных.
Общий алгоритм итерационных методов решения СНАУ установившегося режима
1) Задание начальных приближений вектора неизвестных U (0) =Uном.
Как правило, в качестве начальных приближений напряжений задают номи-нальные напряжения узлов Uном.В некоторых случаях, в качестве начальных приближений напряжений принимают значения, полученные в предыдущих близких расчетах для данной схемы;
2) Задание точности расчета E, предельного количества итераций nпред.,
начального значения счетчика итераций к=0 и других параметров расчета;
3) Выполнение итерации в соответствии с формулой (6):
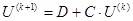
4) Контроль завершения итерационного процесса:
Если условие не выполняется, то изменяем счетчик итераций (к=к+1) и возвращаемся к пункту (3). Повторяем расчет при новых приближениях неизвестных.
Если условие выполняется для всех значений Ui, то итерационный процесс завершается, найденные на последней итерации приближения неизвестных U ( k +1) принимаются в качестве искомых значений с заданной точностью.
Итерационные методы дают последовательность приближенных значе-ний неизвестных, сходящуюся к точному решению. Это означает, что су-ществует предел последовательности:

здесь U (* ) — точное решение при 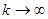
Таким образом, точное решение может быть получено лишь в резуль-тате бесконечного итерационного процесса. Всякий вектор U ( k ) , полученный на к-ой итерации, является приближенным решением системы уравнений.
Вектор погрешности этого приближенного решения:
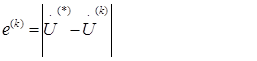
Так как точное решение U (*) заранее неизвестно, то о погрешности судят по разности значений на смежных итерациях (к+1) и к, то есть по вектору поправок:
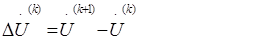
Если 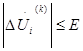
Такой подход к контролю завершения итерационного процесса — не единственный и не очень надежный, так как возможно такое незначительное изменение приближений от итерации к итерации даже вдали от решения.
Более строгим и надежным способом контроля завершения итераци-онных процессов является контроль невязок уравнений. Невязка уравнения – разность между левой и правой частями уравнения. Её значение получаем при подстановке в уравнения системы (2) очередного приближения неиз-вестных. Например, для 1-го уравнения:
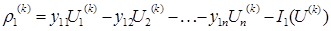
Для УУР невязка уравнения соответствует расчетному небалансу тока (мощ-ности) в узле. При подстановке точных значений неизвестных U1 (*) ,U2 (*) ,…,Un (*) невязки будут равны нулю:

То есть если итерационный процесс сошелся, то невязки близки к нулю. И чем дальше приближение Ui ( k ) от точного решения, тем больше величина не-вязок. В общем случае вектор невязок можно определить:
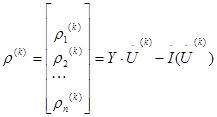
Итерационный процесс сошелся, если выполняются условия завершения итерационного процесса:

Это условие является более надежным критерием окончания итерационного процесса.
Достаточным условием сходимости итерационного процесса для урав-нений установившегося режима является:
Т.о. условие сходимости определяется только соотношением элементов матрицы проводимостей Y . В ней диагональные элементы Уіі (собственные проводимости узлов) неравны нулю. Как правило, диагональные элементы матрицы проводимостей больше или равны суммы недиагональных элемен-тов. Т.е. при правильном формировании матрицы, это условие сходимости выполняется всегда.
Два вида сходимости итерационных процессов:
1. Экспоненциальный (апериодический):
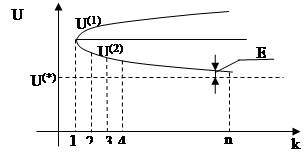 |
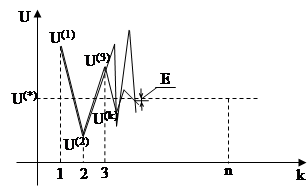
В случае не сходящихся или расходящихся итерационных процессов, нужно проверять правильность расчетов параметров схемы замещения, правильность расчета элементов и формирования матрицы проводимос-тей, анализировать величины токов и мощностей в заданных узлах.
Пример использования метода Ньютона для решения УУН
УЧЕТ КОМПЛЕКСНОГО ХАРАКТЕРА
ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ И РЕЖИМА[1]
Система уравнений узловых напряжений для цепи переменного тока:
 . . | (9.7) |
При решении на ЭВМ системы уравнений узловых напряжений для сети переменного тока, как правило, она приводится к системе действительных уравнений порядка 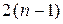

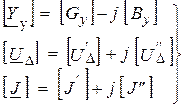 | (9.8) |
Подставляя (9.8) в (9.7), получим:
 | (9.9) |
Уравнение (9.9) переписываем, разделяя действительные и мнимые слагаемые.
 . . | (9.10) |
 . . | (9.11) |
Иными словами, систему уравнений узловых напряжений для цепи переменного тока можно записать в виде блочного матричного уравнения:
 | (9.12) |
Выражение (9.12) является системой действительных уравнений порядка 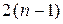
ОПИСАНИЕ РАСЧЕТА УР С ПОМОЩЬЮ ВЕКТОР-ФУНКЦИИ
Нелинейные уравнения установившегося режима в общей форме можно записать в виде системы неявных функций:
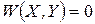 | (9.53) |
где 
Эти уравнения связывают между собой параметры установившегося режима электрической системы. Часть параметров режима задана (независимые переменные 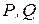

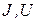

Число зависимых переменных 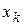




Разделение параметров режима на зависимые и независимые переменные играет важную роль при оптимизации режимов, при определении предельных по статической апериодической устойчивости режимов и при исследовании существования и единственности решения уравнений установившегося режима.
При расчетах установившегося режима вектор независимых переменных задан, то есть 
 | (9.54) |
Число уравнений в этой системе также равно числу зависимых переменных 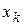

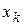
МЕТОД НЬЮТОНА
Метод Ньютона для решения систем нелинейных уравнений представляет собой обобщение на многомерный случай метода касательных, применяемого для решения одного нелинейного уравнения.
Идея метода Ньютона состоит в последовательной замене на каждой итерации системы нелинейных уравнений некоторой линейной системой, решение которой дает значения неизвестных, более близкие к решению нелинейной системы, чем исходное приближение. Поясним идею этого метода на примере решения уравнения
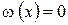 | (5.4) |
Решение уравнения 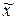 — точка, в которой кривая — точка, в которой кривая  проходит через нуль (рисунок 5.1): Рисунок 5.1- Графическая иллюстрация метода Ньютона проходит через нуль (рисунок 5.1): Рисунок 5.1- Графическая иллюстрация метода Ньютона |  |
Зададим начальное приближение к решению уравнения 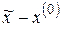
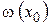

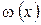

 | (5.5) |
Выражению (5.5) соответствует касательная к функции, проведенная в точке 
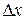
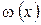

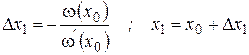 | (5.6) |
Полученную точку 
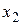
Аналогично определяется решение для системы нелинейных уравнений. Рекуррентное выражение, представленное в матричной форме записи, имеет вид:
 | (5.7) |
где 

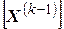

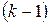
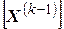
Пример использования метода Ньютона для решения УУН
Для электрической сети, представленной на рисунке 5.2, определить напряжения в узлах, используя метод Ньютона (три итерации).
Для рассматриваемой схемы электрической сети может быть записана система нелинейных УУН в форме баланса токов:
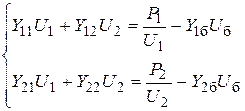 | (5.8) |
 | |
| Рисунок 5.2 | Схема электрической сети. |
Для решения методом Ньютона система УУН (5.8) представляется в форме баланса мощностей
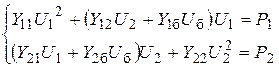 | (5.9) |
И приводится к виду
 |
Рекуррентное выражение метода Ньютона:
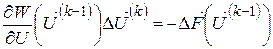 , , | (5.10) |
Где: 1) элементы матрицы Якоби вычисляются по формулам:
 , , |
2) вектор невязок вычисляется в точке 
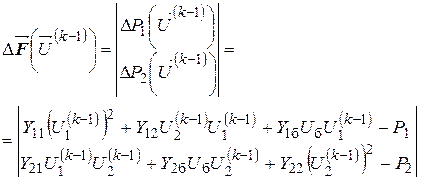 , , |
3) 
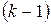

Новые напряжения вычисляются по выражению
 | (5.11) |
Для схемы электрической сети, представленной на рисунке 5.2, исходная система (5.9) имеет вид:
 |
Начальное приближение: 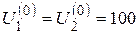
Вектор невязок записывается:
Элементы матрицы Якоби:
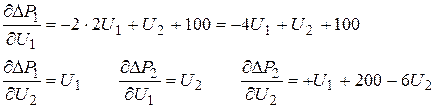 |
Для заданного начального приближения 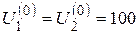
 |
Подставляем все найденные величины в 
 |
Решив ее, находим:
 |
По выражению (5.11):
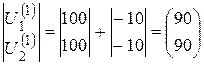 кВ кВ |
 |
 |
Система двух линейных уравнений:
 |
Решив ее, находим:
 |
По выражению (5.11):
 кВ кВ |
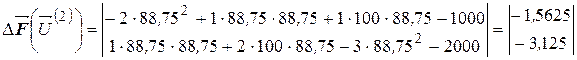 |
 |
Система двух линейных уравнений:
 |
Решив ее, находим:
 |
По выражению (5.11):
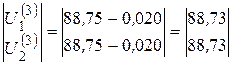 кВ кВ |
Вектор невязок для 4-ой итерации составил бы:
Решение уравнений установившегося режима работы электрической системы
ВВЕДЕНИЕ
Дисциплина «Математические задачи энергетики» среди других, изучаемых студентами специальности 0303, занимает одно из важных мест в общем процессе подготовки инженера-электрика. Она дает математическую основу для изучения таких специальных дисциплин, как электроснабжение промышленных предприятий, переходные процессы в системах электроснабжения, электрические системы и сети и другие.
Основная цель изучаемой дисциплины состоит в получении необходимых теоретических знаний и практических навыков решения математических задач, возникающих при эксплуатации и проектировании систем электроснабжения (СЭС), умений приспособить математику и ее приложения к задачам специальности. Задача дисциплины – связать математику как общетеоретическую дисциплину с практическим ее применением в работе инженера, дать корректный практический аппарат для инженерных исследований в области электроснабжения.
В соответствии с учебным планом по данной дисциплине предусматривается выполнение двух контрольных заданий. Выполненные контрольные задания высылаются студентами в институт для проверки их преподавателями кафедры. Студенты,
выполнившие контрольные задания, допускаются к сдаче экзамена по дисциплине.
В настоящих указаниях приводятся программа дисциплины «Математические задачи энергетики» с вопросами для самопроверки, контрольные задания, методические указания по их выполнению и список рекомендуемой литературы.
ПРОГРАММА ДИСЦИПЛИНЫ
Основные задачи в области электроснабжения. Предмет дисциплины, его задачи и место в учебном плане. Характеристика основных разделов дисциплины.
Решение уравнений установившегося режима работы электрической системы
2.1.1 Основные понятия и определения: энергетическая и электрическая системы, электрическая сеть, линия электропередачи, узел, ветвь, замкнутый контур, режим системы. Схема замещения электрической системы и ее элементы. Уравнения узловых напряжений (УУН) и уравнения контурных токов (УКТ) описывающие установившийся режим работы электрической системы.
Вопросы для самопроверки:
1. Назовите основные элементы электрической системы и их назначение.
2. Дайте характеристику основных видов режимов электрической сети.
3. Что такое параметры режима и системы?
4. Что представляет собой схема замещения электрической системы?
5. Какой узел принимается за узел баланса?
2.1.2 Основы применения алгебры матриц к расчету электрических сетей. Матрицы, основные определения. Сложение, вычитание и умножение матриц. Обратные матрицы и способы их определения. Разделение матриц на блоки. Матрицы, используемые для записи и решения УУН и УКТ.
Элементы теории графов: графы схем, дерево и хорды графов. Матрицы соединений, независимых контуров, собственных и взаимных проводимостей и сопротивлений. Применения матриц соединений и контуров.
Вопросы для самопроверки:
1. Перечислите основные виды матриц.
2. Что такое транспонированная матрица?
3. Как вычислить обратную матрицу?
4. Что устанавливают 1 и 2 матрицы соединений?
5. Чем отличается связанный граф от несвязанного?
6. Запишите в матричной форме УКТ и УУН для какой-либо электрической сети.
2.1.3 Решение системы уравнений узловых напряжений. Линеаризация системы УУН и их решение с помощью обращения матрицы узловых проводимостей. Трудности получения и использования обратной матрицы. Применение метода Гаусса для решения линеаризованных УУН. Использование слабой заполненности матриц. Применение итерационных методов (простой итерации, Зейделя, Ньютона) для решения линеаризованной и нелинейной системы УУН. Сравнительная характеристика применяемых методов решения установившегося режима электрической системы и области их применения.
Вопросы для самопроверки:
1. В чем сущность линеаризации схем замещения?
2. Чем отличается метод Зейделя от метода простой итерации?
3. Какие виды сходимостей итерационного процесса вы знаете?
4. В чем основное достоинство метода Ньютона для решения системы УУН?
5. Назовите основные области применения итерационных методов для решения электроэнергетических задач.
Решение и анализ уравнений электромеханических переходных процессов в электрической системе
Дифференциальные уравнения электромеханических переходных процессов в одномашинной и многомашинной системах. Их численное решение методами Эйлера и Рунге-Кутта.
Структурные схемы и характеристики их элементов. Получение передаточной функции системы по ее структурной схеме. Частотный коэффициент усиления, частотные характеристики системы.
Метод оценки статической устойчивости состояний равновесия линеаризованных систем дифференциальных уравнений. Характеристический определитель и его корни. Методы приближенного определения корней. Алгебраические критерии устойчивости Рауса и Гурвица. Принцип аргумента и частотные критерии устойчивости Михайлова и Найквиста. Применение алгебраических и частотных критериев для анализа устойчивости положения равновесия в электромеханической системе.
Вопросы для самопроверки:
1. В каких задачах энергетики применяются дифференциальные уравнения?
2. Назовите способы решения дифференциальных уравнений электромеханического переходного процесса.
3. Что понимается под статической устойчивостью системы?
4. Перечислите основные элементы структурной схемы
5. Какие основные типовые линейные звенья Вы знаете?
6. Что такое передаточная функция системы?
7. Назовите Алгебраические критерии устойчивости.
8. Как оценивается устойчивость системы автоматического регулирования с использованием кривой Михайлова?
9. В чем сущность метода Д-разбиения?
Применение методов теории вероятностей к решениям задач электроснабжения
Техническая и математическая постановка задачи. Случайные события в энергетике. Случайные величины в энергетике. Основные числовые характеристики случайных величин: математическое ожидание, дисперсия, стандартное отклонение и моменты случайной величины. Случайные процессы в энергетике. Применение метода Монте-Карло в электроэнергетике.
Вопросы для самопроверки:
1. Дайте определение основным понятиям в теории вероятностей: случайному событию, случайной величине, случайной функции и случайному процессу.
2. Перечислите законы вероятности сложных событий для независимых случайных событий.
3. Что понимается под условной вероятностью события?
4. Назовите основные числовые характеристики случайной величины.
5. В чем сущность метода Монте-Карло?
Основные понятия математического программирования и его применение в электроэнергетике
Выпуклые функции и множества. Основные определения выпуклой функции и выпуклого множества. Способы проверки выпуклости. Основные понятия линейного программирования. Формулировка задачи линейного программирования. Канонические формы. Базисное решение. Алгоритм симплекс-метода решения общей задачи линейного программирования с ограничениями в виде равенств. Учет неравенства в задаче линейного программирования. Задача выпуклого программирования. Необходимые и достаточные условия для решения задачи выпуклого программирования. Двойственность и множители Лагранжа. Алгоритм методов решения задачи нелинейного программирования. Применение методов выпуклого программирования для решения энергетических задач (развитие электрической сети, оптимизация режима).
Задачи дискретного и динамического программирования. Методы решения этих задач. Применение методов математической статистики для прогнозирования нагрузок и стоимостей элементов электрической системы в оптимизационных задачах.
Литература: 3, 4, 6.
Вопросы для самопроверки:
1. Назовите способы проверки выпуклостей.
2. Как формулируется задача линейного программирования?
3. Что такое базисное решение задачи линейного программирования?
4. Для решения каких задач применяется симплексный метод?
5. В чем состоит основная задача выпуклого программирования?
6. Назовите необходимые и достаточные условия решения
задачи выпуклого программирования.
7. Что понимается под дискретной задачей?
8. Что Вы понимаете под оптимизационными задачами?
КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ
Программой предусматривается выполнение двух контрольных заданий. В первом контрольном задании решаются задачи № 1 и 2 на применение алгебры матриц в задачах электроснабжения. Во втором контрольном задании решаются задачи № 3 и 4, соответствующие разделам 2.2 и 2.4 программы дисциплины.
Каждая задача в контрольных заданиях включает в себя 10 вариантов. Номер варианта выбирается в соответствии с последней цифрой шифра зачетной книжки студента. Студенты, имеющие последней цифрой шифра «1», выполняют первый вариант, при последней цифре «0» — десятый вариант.
Контрольные задания выполняются на листах ученических тетрадей. Разрешается писать на обеих сторонах листа. Рисунки в работе могут выполняться как на самих листах ученических тетрадей, так и на миллиметровой бумаге, имеющей размеры листа ученической тетради. Листы тетради должны иметь поля и быть пронумерованы. Каждая задача должна начинаться с новой страницы, иметь подробное условие задачи и содержать необходимые пояснения по ее решению. Исправления, вносимые по решению задач, должны быть аккуратны и разборчивы. В конце контрольного задания помещается список использованной литературы. Оформленная работа должна иметь подпись студента, дату выполнения, шифр зачетной книжки, точный домашний адрес. Допускается оформление контрольных заданий № 1 и 2 в одной тетради.
Задача № 1. Для графа электрической сети, приведенного на рисунке 3.1, записать первую и вторую матрицу соединения (инциденций). Нарисовать исходный граф и два из возможных вариантов деления его на дерево и хорды. Под каждым их рисунков сделать соответствующую надпись «дерево» или хорды».
Варианты заданий приведены на рисунке 3.1.
Рисунок 3.1 – Варианты заданий к задаче № 1
Перед составлением матриц соединений необходимо пронумеровать ветви, задаться их направлением, а также выбрать независимые замкнутые контуры и направление их обхода.
Первую матрицу соединений составить только для независимых узлов, т.е. за исключением базисного. В качестве базисного узла принять узел 1.
При выполнении задачи рекомендуется изучить § 1-3/1/.
Задача № 2. Найти узловые напряжения и токораспределение в схеме, показанной на рисунке 3.2, методом узловых напряжений, используя обращение матрицы узловых проводимостей и один из традиционных способов решения уравнений (см. таблицу 3.1). За балансирующий и базисный узел принять узел 0, считая, что
Данные о задающих токах приведены в таблице 3.2.
Рисунок 3.2 – Схема электрической сети
Таблица 3.1 – Варианты заданий
| Варианты заданий | Метод решения задачи |
| Простой итерации | |
| Зейделя | |
| Ньютона | |
| Зейделя | |
| Ньютона | |
| Простой итерации | |
| Ньютона | |
| Зейделя | |
| Простой итерации | |
| Ньютона |
Таблица 3.2 – Данные о задающих токах
| № уз | Значения задающих токов в узлах, А | |||||||||
| Варианты заданий | ||||||||||
| 1 2 3 | -140 -120 0 | -125 -130 -115 | -115 -130 -130 | 0 -150 -140 | -145 -125 -110 | -115 -120 -120 | -125 0 -165 | -140 -130 -150 | -125 -125 -130 | -110 -120 -130 |
Сопротивление ветвей принять:
Для решения задачи указанными методами необходимо вначале определить матрицу узловых проводимостей. Порядок ее получения приведен в § 1-4/1/, а также в разделе 4.2 данных указаний.
Задача № 3. Система автоматического регулирования описывается характеристическим уравнением четвертого порядка:
Дать оценку устойчивости данной системы, используя критерии Гурвица, Рауса и путем построения кривой Михайлова. Выявить характер неустойчивости (апериодический или колебательный) в случае неустойчивости системы.
Значения коэффициентов характеристического уравнения системы приводятся в таблице 3.3.
Таблица 3.3 – Данные о коэффициентах характеристического уравнения системы
| Варианты заданий | ||||||||||
 | 0,1 | 0,5 | 2,0 | 0,3 | 1,7 | 2,4 | 0,05 | 0,7 | 0,17 | 2,1 |
 | 0,5 | 0,9 | 3,6 | 0,2 | 1,7 | 0,65 | 9,4 | |||
 | 4,1 | 5,2 | 3,8 | 4,2 | 20,0 | |||||
 | 0,5 | 3,0 | 1,8 | |||||||
 | 1,8 | 1,5 | 1,1 | 0,3 | 1,5 | 0,9 |
При выполнении данной задачи рекомендуется предварительно познакомиться с теоретическим положениями рассматриваемых вопросов (см. § 4-7, § 5-1, § 5-5/1/) и пояснениями, приведенными в разделе 4.7 данных указаний.
Задача № 4. Найти минимум целевой функции задачи линейного программирования, заданной в канонической форме. Задачу решить комплексным методом.
Уравнения функций цели и систем ограничений по вариантам приведены в таблице 3.4.
Таблица3.4 – Уравнения функции цели и систем ограничений
| № | Целевая функция | Система ограничений | Граничные условия |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  |
Продолжение таблицы 3.4
 |  |  |
 |  |  |
Решение УУН методом Ньютона
При решении данным методом делается допущение, что в узлах схемы (рисунок 3.2) включены только активные нагрузки, определяемые как


Система нелинейных уравнений, описывающих установившийся режим работы сети, записывается в развернутом виде как

n – число независимых узлов, а задающие точки в узлах представлены как
В соответствии с положением метода [6], итерационных процессов определении напряжений в узлах схемы ведется по решению уравнения, которое в матричном виде записываются как

где K – номер итерации,

А значения функции 

В частности, для рассматриваемой схемы (рисунок 3.2) и принятых упущениях эта матрица запишется в виде
Контроль сходимости осуществляется по методу невязок, то есть условие
Должно осуществляться для всех невязок (небалансов) системы уравнений (4.1).
Учитывая достаточно большой объем вычислений данным методом, допускается провести расчет только трех итераций. Начальные значения напряжений узлах и токораспределение в схеме принимается аналогично рекомендациям, изложенным выше. Достаточно подробно изложены методы, описанные в [1,5].
СОДЕРЖАНИЕ
2. ПРОГРАММА ДИСЦИПЛИНЫ
1.1 Решение уравнений установившегося режима работы электрической системы
1.2 РЕШЕНИЕ И АНАЛИЗ УРАВНЕНИЙ ЭЛЕКТРОМЕХАНИЧЕСКИХ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКОЙ СИСТЕМЕ
1.3 ПРИМЕНЕНИЕ МЕТОДОВ ТЕОРИИ ВЕРОЯТНОСТЕЙ К РЕШЕНИЮ ЗАДАЧ ЭЛЕКТРОСНАБЖЕНИЯ
1.4 ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ И ЕГО ПРИМЕНЕНИЕ В ЭЛЕКТРОЭНЕРГЕТИКЕ
2. КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ
3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
3.1 КРАТКИЕ СВЕДЕНИЯ О МАТРИЦАХ И ОСНОВНЫЕ ОПЕРАЦИИ НАД НИМИ
3.2 МАТРИЦЫ СОЕДИНЕНИЙ И УЗЛОВЫХ ПРОВОДИМОСТЕЙ
3.3 РЕШЕНИЕ ЛИАНЕРИЗОВАННЫХ уун МЕТОДОМ ОБРАЩЕНИЯ МАТРИЦЫ УЗЛОВЫХ ПРОВОДИМОСТЕЙ
3.4 РЕШЕНИЕ ЛИАНЕРИЗОВАННЫХ уун МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ
3.5 РЕШЕНИЕ ЛИАНЕРИЗОВАННЫХ уун МЕТОДОМ зЕЙДЕЛЯ
3.6 РЕШЕНИЕ уун МЕТОДОМ НЬЮТОНА
3.7 ОЦЕНКА УСТОЙЧИВОСТИ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ АЛГЕБРАИЧЕСКИХ И ЧАСТОТНЫХ КРИТЕРИЕВ
3.8 РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛЕКС-МЕТОДОМ
сПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
Дисциплина «Математические задачи энергетики» среди других, изучаемых студентами специальности 0303, занимает одно из важных мест в общем процессе подготовки инженера-электрика. Она дает математическую основу для изучения таких специальных дисциплин, как электроснабжение промышленных предприятий, переходные процессы в системах электроснабжения, электрические системы и сети и другие.
Основная цель изучаемой дисциплины состоит в получении необходимых теоретических знаний и практических навыков решения математических задач, возникающих при эксплуатации и проектировании систем электроснабжения (СЭС), умений приспособить математику и ее приложения к задачам специальности. Задача дисциплины – связать математику как общетеоретическую дисциплину с практическим ее применением в работе инженера, дать корректный практический аппарат для инженерных исследований в области электроснабжения.
В соответствии с учебным планом по данной дисциплине предусматривается выполнение двух контрольных заданий. Выполненные контрольные задания высылаются студентами в институт для проверки их преподавателями кафедры. Студенты,
выполнившие контрольные задания, допускаются к сдаче экзамена по дисциплине.
В настоящих указаниях приводятся программа дисциплины «Математические задачи энергетики» с вопросами для самопроверки, контрольные задания, методические указания по их выполнению и список рекомендуемой литературы.
ПРОГРАММА ДИСЦИПЛИНЫ
Основные задачи в области электроснабжения. Предмет дисциплины, его задачи и место в учебном плане. Характеристика основных разделов дисциплины.
Решение уравнений установившегося режима работы электрической системы
2.1.1 Основные понятия и определения: энергетическая и электрическая системы, электрическая сеть, линия электропередачи, узел, ветвь, замкнутый контур, режим системы. Схема замещения электрической системы и ее элементы. Уравнения узловых напряжений (УУН) и уравнения контурных токов (УКТ) описывающие установившийся режим работы электрической системы.
Вопросы для самопроверки:
1. Назовите основные элементы электрической системы и их назначение.
2. Дайте характеристику основных видов режимов электрической сети.
3. Что такое параметры режима и системы?
4. Что представляет собой схема замещения электрической системы?
5. Какой узел принимается за узел баланса?
2.1.2 Основы применения алгебры матриц к расчету электрических сетей. Матрицы, основные определения. Сложение, вычитание и умножение матриц. Обратные матрицы и способы их определения. Разделение матриц на блоки. Матрицы, используемые для записи и решения УУН и УКТ.
Элементы теории графов: графы схем, дерево и хорды графов. Матрицы соединений, независимых контуров, собственных и взаимных проводимостей и сопротивлений. Применения матриц соединений и контуров.
Вопросы для самопроверки:
1. Перечислите основные виды матриц.
2. Что такое транспонированная матрица?
3. Как вычислить обратную матрицу?
4. Что устанавливают 1 и 2 матрицы соединений?
5. Чем отличается связанный граф от несвязанного?
6. Запишите в матричной форме УКТ и УУН для какой-либо электрической сети.
2.1.3 Решение системы уравнений узловых напряжений. Линеаризация системы УУН и их решение с помощью обращения матрицы узловых проводимостей. Трудности получения и использования обратной матрицы. Применение метода Гаусса для решения линеаризованных УУН. Использование слабой заполненности матриц. Применение итерационных методов (простой итерации, Зейделя, Ньютона) для решения линеаризованной и нелинейной системы УУН. Сравнительная характеристика применяемых методов решения установившегося режима электрической системы и области их применения.
Вопросы для самопроверки:
1. В чем сущность линеаризации схем замещения?
2. Чем отличается метод Зейделя от метода простой итерации?
3. Какие виды сходимостей итерационного процесса вы знаете?
4. В чем основное достоинство метода Ньютона для решения системы УУН?
5. Назовите основные области применения итерационных методов для решения электроэнергетических задач.
http://poisk-ru.ru/s12069t3.html
http://zdamsam.ru/a4829.html