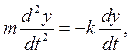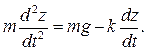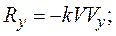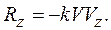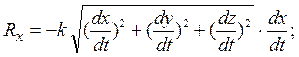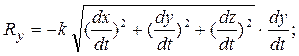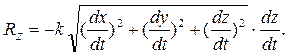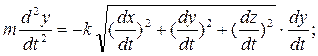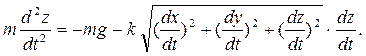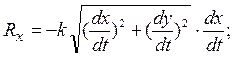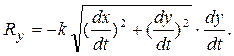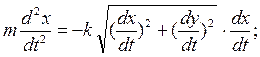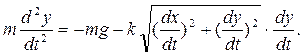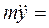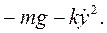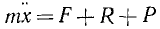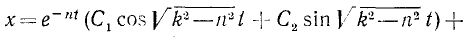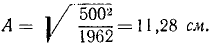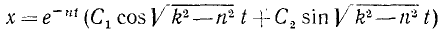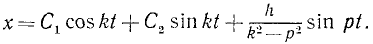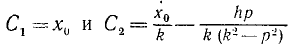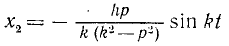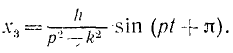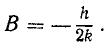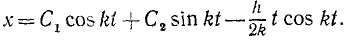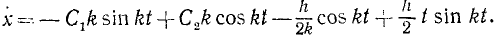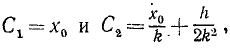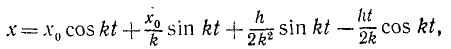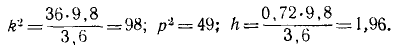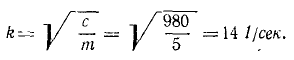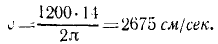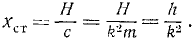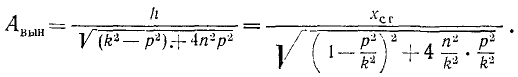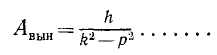Сила сопротивления в дифференциальных уравнениях

Составление дифференциальных уравнений.

Исследование движения материальной точки

Под действием силы тяжести в сопротивляющейся среде

В данной задаче проводится исследование движения материальной точки, находящейся под действием силы тяжести и силы сопротивления, целью которого является определение всех кинематических параметров, характеризующих это движение.

Задача относится к классу основных задач теоретической механики, и ее решение проводится на основе дифференциальных уравнений, описывающих движение материальной точки.

Решение задачи состоит из следующих операций:

1. составление дифференциальных уравнений,

2. определение начальных условий,

3. решение дифференциальных уравнений.

Составление дифференциальных уравнений.

Дифференциальные уравнения движения точки имеют вид

,

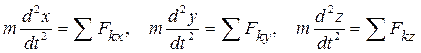
где m – масса материальной точки, x, y, z – ее координаты в произвольный момент времени, F_kx, F_ky, F_kz — проекции приложенных к этой точке сил на оси координат.

Поскольку правые части этих уравнений не зависят от содержания конкретной задачи, составление дифференциальных уравнений сводится к определению суммы проекций всех приложенных к точке сил на выбранные оси координат. Для того, чтобы оформить правую часть каждого дифференциального уравнения, необходимо выполнить следующие действия

1. Выбрать систему координат, начало которой следует совместить с известным по условию задачи положением точки, а оси координат направить так, чтобы координаты движущейся точки вблизи начального положения были положительными.

2. Провести анализ каждой действующей на точку силы: определить ее направление и закономерности изменения, изобразить на чертеже и определить проекции на каждую координатную ось. Сложив проекции всех сил на каждую координатную ось, получим соответствующие правые части дифференциальных уравнений.

Составим дифференциальные уравнения точки, движущейся под действием силы тяжести в сопротивляющейся среде.

Выберем неподвижную систему координат Оxyz так (рис. 1)

чтобы относительно нее было удобно определять положение движущейся точки М. Совместим начало координат с начальным положением точки, ось z направим вертикально вверх, горизонтальные оси координат Ох и Оу направим так, чтобы при небольшом отклонении точки от начального положения ее координаты х и у были положительными.

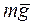
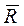
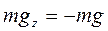
1.2. Проведем анализ действующих на точку сил. В выбранной системе координат (рис.1) изобразим материальную точку и покажем действующие на нее силу тяжести , силу сопротивления и определим их проекции на выбранные оси координат.

Сила тяжести направлена вертикально вниз, поэтому ее проекции на горизонтальные оси Ох и Оу равны нулю, проекция на ось z равна .

Силы сопротивления появляются в том случае, когда тело движется в какой-либо среде. Так, например, на тело, движущееся в воздухе или воде, действует со стороны этих сред сила, препятствующая движению. Действующая на тело сила сопротивления всегда направлена противоположно скорости движения. Когда относительная скорость обращается в ноль, сила сопротивления исчезает. Зависимость силы сопротивления от скорости движения носит в общем случае сложный характер. Многочисленными экспериментами установлено, что при медленном движении тела в газообразной или жидкой среде силы сопротивления пропорциональны первой степени скорости.

При более высоких скоростях имеет место так называемый квадратный или гидравлический закон сопротивления.

Наконец, при очень больших скоростях движения зависимость оказывается более сложной, однако, как в предыдущих вариантах с достаточной степенью точности можно считать, что сила сопротивления зависит только от скорости и всегда направлена против скорости.

Определим проекции сил сопротивления на оси координат для первых двух случаев.

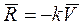
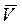
Пусть сила сопротивления прямо пропорциональна величине скорости точки. Такая сила может быть представлена в виде векторной формулы , где k — коэффициент пропорциональности; — вектор скорости точки.

Проекции силы сопротивления на оси координат равны:

; ; .

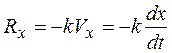
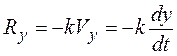
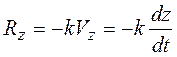
Дифференциальные уравнения движения точки принимают вид

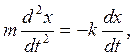
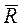
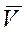
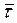
Пусть величина силы сопротивления, действующей на точку, пропорциональна квадрату скорости точки: R = kV 2. . Векторы и направлены по касательной к траектории точки в противоположные стороны, единичный вектор — в сторону скорости движения точки.

Тогда 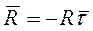, где R = kV 2.

Значит ,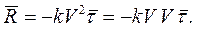

Заменим ,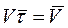

Следовательно, вектор силы сопротивления равен

.

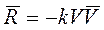
Проекции этого векторного равенства на оси координат будут равны

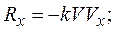
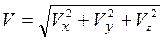
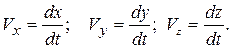
Модуль вектора скорости , проекции скорости на оси координат .

Тогда, проекции силы сопротивления на оси координат будут равны

Дифференциальные уравнения в данном случае будут записаны в виде

Если точка движется в вертикальной плоскости Оху, проекции силы сопротивления на оси координат будут равны

В этом случае будет два дифференциальных уравнения

В том случае, когда начальная скорость точки направлена вертикально по оси Оу, движение точки окажется прямолинейным. Такому движению будет соответствовать одно дифференциальное уравнение

2.Определение начальных условий заключается в том, чтобыв выбранной системе координат определить координаты точки и проекции ее скорости на оси координат в начальный момент времени. Значения указанных характеристик зависят от условия задачи и выбранной системы координат. В результате необходимо записать полученные значения при t = 0: x = x₀, y = y₀, z = z₀,

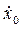
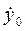
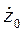
V_x= , V_y = , V_z = .

Если движение точки является плоским относительно системы координат Оху, то соответствующие начальные условия должны быть записаны в виде:

V_x= 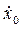, V_y = .

3.Решение дифференциальных уравнений. В данной работе предлагается графическое решение дифференциальных уравнений, описывающих движение материальной точки на основе компьютерной программы Mathcad.

Задание Д -2.

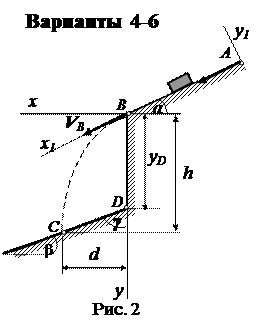
Тело массой m движется из точки А по участку АВ = l наклонной плоскости, составляющей угол α с горизонтом, в течение τ секунд. Его начальная скорость V_A, коэффициент трения скольжения тела по плоскости равен f. Силой сопротивления на данном участке пренебречь.

В точке В тело покидает плоскость со скоростью V_В и падает со скоростью V_С в точку С на наклонную или горизонтальную плоскость (варианты 20 – 21, 25-30) или ударяется о вертикальную плоскость(варианты 22-24), находясь в воздухе Т секунд. Положение плоскости определяется углом наклона (β или γ) или параметрами точек D и D₁, через которые она проходит.

При движении в воздухе на тело действует сила сопротивления, пропорциональная скорости (варианты 1-24) или пропорциональная квадрату скорости (варианты (24-30), коэффициент пропорциональности равен k.

1. Определить все характеристики движения тела по наклонной плоскости АВ: уравнение движения, зависимость скорости и ускорения от времени, время движения по наклонной плоскости, если задана ее длина l, или ее длину, если задано время τ, значение скорости V_В в точке В.

2. Принимая во внимание силу сопротивления, составить дифференциальные уравнения движения тела в воздухе, определить траекторию этого движения, построить графики зависимости скорости и ускорения от времени, определить время движения в воздухе, установить место падения тела на заданную плоскость, определив координаты точки падения, вычислить конечную скорость .

3. Определить движение тела в воздухе без учета силы сопротивления, найти траекторию, скорость и ускорение этого движения, установить место удара тела о наклонную плоскость и его скорость в этот момент.

4. Сравнить движение тела в воздухе при наличии силы сопротивления и без нее.

Варианты 1-3.

Вариант 1. Дано: m = 2 кг,

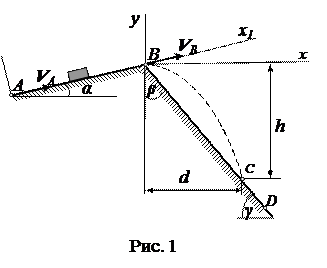
α = 15 0 ; f = 0,1; V_A = 25 м/c;

l = 5 м; β = 40 0 ; k =0,4.

Вариант 2.Дано: m = 0,5 кг,

α = 20 0 ; f = 0,12; V_A = 20 м/c;

τ = 3 с; γ = 45 0 ; k =2.

Вариант 3.Дано: m = 3 кг,

α = 18 0 ; f = 0,1; V_A = 16 м/c;

Вариант 4.Дано: m = 1,5 кг;

Вариант 5. Дано: m = 2 кг;

τ = 3 c; β = 60 0 ; y_D = — 30 м;

Вариант 6. Дано: m = 1,5 кг;

Варианты 6-9

Вариант 7. Дано: m = 2 кг, α = 15 0 ; V_A = 20 м/c; f = 0,1; l = 5 м; k =0,4; β = 30 0 ;

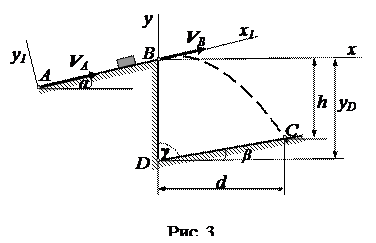
Вариант 8.Дано: m = 1 кг, α = 20 0 ; f = 0,12; τ = 3 с;

Вариант 9.Дано: m = 3 кг, α = 18 0 ;V_A = 16 м/c; f = 0,1; τ = 4 с; γ =120 0 ; y_D =-20 м.

Варианты 10 – 12

Вариант 10. Дано: m = 60 кг; α = 15 0 ; V_A = 18 м/c; f = 0; l = 6 м; β = 40 0 ; y_D = -15 м;

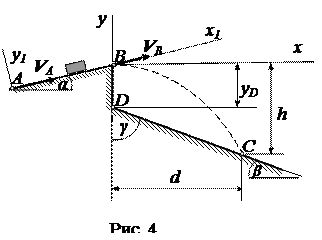
Вариант 11. m = 60 кг;

Вариант 12. Дано: m = 50 кг; α =20 0 ; V_A = 20 м/c; τ = 2 с;

f = 0,2; β = 60 0 ; y_D = -2,5 м; k = 12;

Варианты 13-15

Вариант 13. Дано: m = 2 кг;

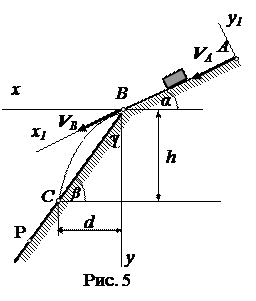
l =10 м; β = 40 0 ; k = 0,3.

Вариант 14. Дано: m = 2 кг;

τ = 3 с; γ = 34 0 ; x_D= 20 м;

Вариант 15. Дано: m = 2 кг;

α =15 0 ; V_A = 3 м/c; τ = 2 с

Варианты 16-18

Вариант 16. Дано: m = 2 кг;

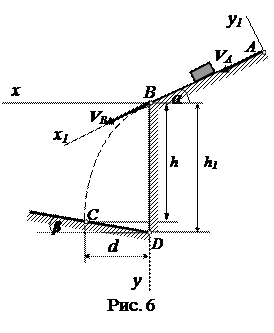
τ = 5 c; f =0,18; β= 15 0 ;

Вариант 17. Дано: m = 2 кг;

l = 8 м; y_D = 38 м; k = 0,36;

Вариант 18. Дано: m = 2 кг;

l = 12 м; β = 40 0 ; y_D =50 м;

Варианты 19-21 Вариант 19. Дано: m = 2 кг, α = 15 0 ; f = 0,1; V_A = 25 м/c; l = 5м, м; γ = 35 0 ; k =0,4.

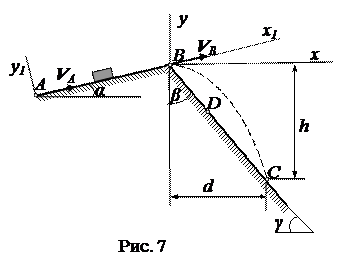
Вариант 20.Дано: m = 0,5 кг,

α = 20 0 ; f = 0,12; τ = 3 с;

Вариант 21.Дано: m = 3 кг,

α = 18 0 ; f = 0,1; V_A = 16 м/c; τ = 3 с; k =0,15; γ = 40 0 .

Варианты 22-24

Вариант 22. Дано: m = 4 кг;

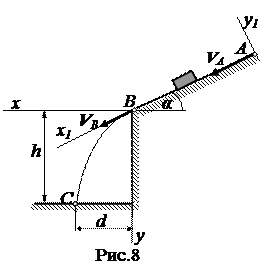
α =25 0 , V_A = 12 м/c; l = 8 м;

Вариант 23. Дано: m = 4 кг;

l = 8 м; h=38 м; k =0,36.

Вариант 24. Дано: m = 4 кг;

τ = 3 c; h =40 м; k = 0, 4.

Варианты 25-27

Вариант 25. Дано: m =0,3 кг;

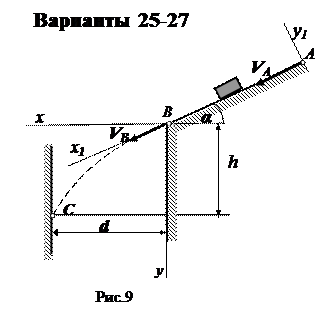
τ = 5 c; d =30 м; k = 0,2.

Вариант 26. Дано: m =0,3 кг;

f = 0,12; α = 15 0 ; τ = 6 c;

Вариант 27. Дано: m =0,3 кг; f = 0,12; α = 15 0 ; V_A = 12 м/c; l = 12 м; d =40 м, k = 0,18.

Варианты 28-30

Вариант 28. Дано: m = 6 кг;

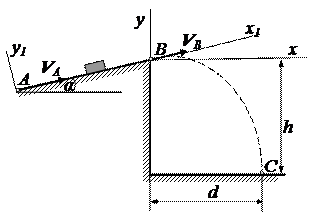
α =15 0 ; f = 0,1; V_A = 25 м/c;

τ= 2 сек; h = 24 м; k =0,09.

Вариант 29. Дано:m = 4 кг;

α = 20 0 ; f =0,1; V_A = 25 м/c;

l =2 5 м; h = 40 м; k =0,06.

Вариант 30. Дано: m = 4 кг;

α = 20 0 ; f = 0,1; V_A = 18 м/c;

Моделирование динамических систем: задача внешней баллистики

Надеюсь что мы с вами набрались достаточно опыта, чтобы смоделировать что-нибудь более серьезное, чем полет камня. Предлагаю такую задачу

Пушка, стреляющая сферическими ядрами сообщает им начальную скорость 400 м/с. Определить траекторию полета снаряда при стрельбе под углом в 35 градусов к горизонту. Поле силы тяжести считать однородным, кривизной Земли пренебречь.

Надо сказать, это пример некорректно поставленной задачи. Во-первых, не сказано учитываем мы, или не учитываем сопротивление воздуха. А если учитываем, то в задаче явно не хватает параметров. К сожалению такого рода постановка задач весьма распространенное явление. Поэтому мы решим задачу для обоих случаев, а нужные параметры введем в неё сами. Заодно научимся чему-то новому. Поехали!

1. Расчетная схема

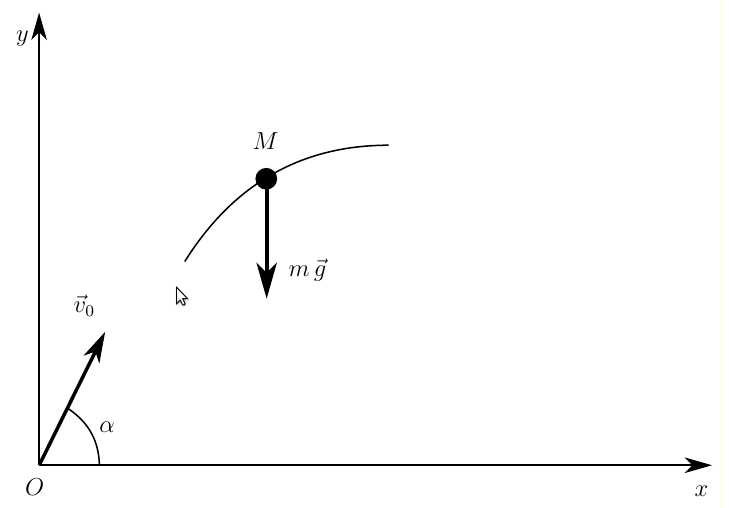
В прошлые разы я сознательно не рисовал никаких схем, чтобы потренировать ваше воображение. Несложно представить себе камень, падающий вертикально вниз. Сейчас задачка посложнее, и без чертежа нам не обойтись.

Подобные чертежи называют расчетной схемой — условным графическим изображением процесса или объекта, выполненным с учетом введенных в задачу допущений.

Обратите внимание, что на схеме нарисовано произвольное положение снаряда, то, в которое он попадет по истечении некоторого времени от начала движения. В задачах динамики так удобнее представить себе взаимное расположение векторов сил и правильно разложить их на осевые проекции. Единственное, что мы показали в начальном положении — вектор начальной скорости. Это пригодится при задании начальных условий.

2. Формализация задачи (без учета сопротивления среды)

Все готово к составлению системы дифференциальных уравнений движения

Мы не учитываем сопротивления воздуха, и у нас всего одна сила: на ось x она проецируется в ноль, на ось y — в истинную величину с минусом. Ведь мы приняли допущение, что поле силы тяжести однородно а Земля плоская. Значит сила тяжести всегда постоянна и направлена вертикально вниз. Как видно, от массы тут ничего не зависит, масса сокращается в обоих уравнениях

Получилась система двух уравнений второго порядка. Нам нужно привести её к форме Коши. Помните что это? Если помните, попробуйте сделать это сами, не заглядывая под спойлер

Все просто, производные координат, это соответствующие проекции скорости

а проекции ускорения — производные от проекций скорости

Получаем систему уравнений в форме Коши

3. Скрипты Octave, или как заново не делать одну и ту же работу

В прошлый раз мы вводили команды в прямо в консоли Octave. Хорошо задачка у нас была маленькая. А если большая? А если хочется поменять параметры? А если хочется вернуться к отложенной работе? А если… Короче говоря, хорошо иметь возможность сохранять свои программы на Octave. И таки тут нет ничего невозможного.

Внизу экрана, под командным окном есть вкладки: Command Window, Editor и Documentation. Вкладка Editor — то что нам нужно. Это редактор скриптов на m-языке. Откроем эту вкладку и введем в неё такой текст

Это ничто иное, как правая часть системы дифференциальных уравнений движения снаряда, в нашей задаче, оформленная в виде функции на m-языке. Смысл тот же самый что и прошлый раз. Только теперь уравнений у нас аж четыре. Ну и ускорение свободного падения берем уже нормальной, взрослой величины. Сохраним этот файл на диске под именем f.m

Внимание! Каждая функция на m-языке требует сохранения в собственный файл, имя которого совпадает с именем функции. В нашем случае функция имеет имя f, значит и файл имеет имя f.

Что за строки, начинающиеся с «%»? А это, братья-апачи, комментарии! Текст, предваренный этим символом в Octave игнорируется интерпретатором. Комментариями не только можно, но и нужно снабжать свои программы, чтобы хотя бы самому в них ориентироваться, не говоря уже о других людях, желающих воспользоваться вашей программой.

Итак, мы задали октаве систему уравнений. Создадим новый файл, назовем его, например, ballistics.m и сохраним там же, где и сохранили предыдущий файл. Начнем решать задачу!

Смысл большинства операций понятен из комментариев. Отдельно поясню начальные условия. У нас четыре фазовых координаты: две декартовы координаты снаряда, две проекции его скорости на оси координат

Для каждой из фазовых координат нужно задать их начальное значение. Логично задать начальное положение в начале координат. Что качается двух других переменных, то это, внимание, начальные величины проекций вектора скорости на оси x и y. Затем я и нарисовал вектор начальной скорости, чтобы легко было найти его проекции на оси

Теперь всё готово. Жмем на кнопку с шестерней и желтым треугольником, чтобы запустить скрипт. В ответ система выдаст окошко

попросит нас добавить путь, по которому лежит скрипт в пути поиска скриптов. Это нужно сделать один раз после загрузки скрипта в редактор или создании нового скрипта. Жмем кнопку «Add. » и получаем результат

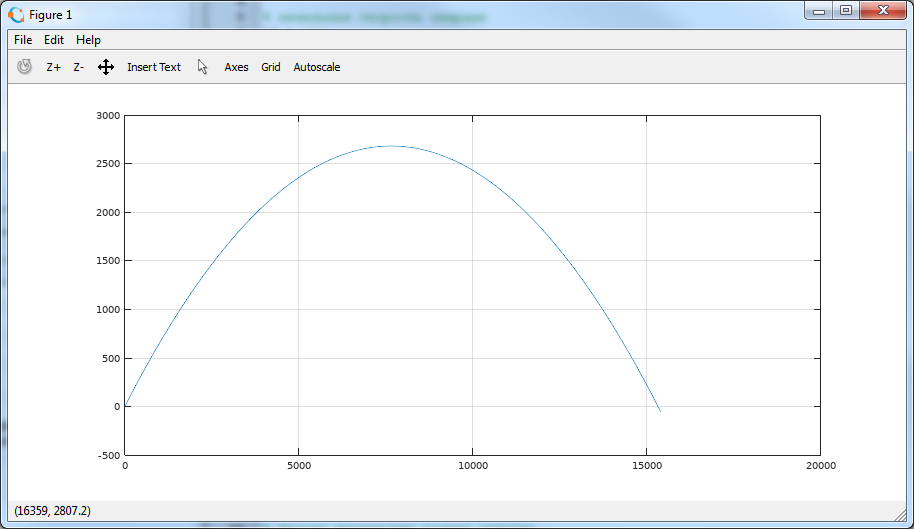
Выглядит многообещающе. Время 10 секунд мало, чтобы наряд приземлился. Меняем значение tend и запускаем скрипт снова, пока не получим похожую картинку

соответствующую tend = 47 секунд. Симуляция закончилась, снаряд пролетел ниже оси x, но это нормально, ведь мы никак не моделируем его встречу с поверхностью.

4. Формализация задачи (с учетом сопротивления среды)

Шар в качестве формы снаряда мы выбрали не случайно. Как его не верти, со всех сторон у него одинаковое сечение — круг (кстати, то той же причина КК «Восток» имел шарообразную форму спускаемого аппарата). А значит, как ни направляй поток воздуха, при обтекании сила сопротивления движению будет одинакова и равна

где c_f = 0.47 — коэффициент лобового сопротивления формы; S — площадь поперечного сечения; = 1.29 кг/м 3 — плотность воздуха; v — скорость набегающего потока, в нашем случае скорость снаряда.

Вектор силы сопротивления всегда будет направлен против вектора скорости. Поэтому перерисуем расчетную схему

Как учесть тот факт, что для любого момента времени вектор направлен против скорости? Очень просто. Мы знаем, что вектор скорости направлен по касательной к траектории. Введем вектор с длинной равной 1 и направленные туда же, куда направлена скорость. Тогда вектор можно выразить через вектор и модуль силы сопротивления

А как найти вектор ? Очень просто, его проекции на оси координат будут равны

Модуль вектора скорости легко выражается через его проекции

Тогда проекции вектора силы сопротивления воздуха на оси координат легко посчитать

И это меняет уравнения движения

Это что же выходит, массу теперь не сократить? Да, теперь динамика полета снаряда будет зависеть от массы. Но на массу никто не запрещает делить, делим на неё оба уравнения

коэффициент, определяющий вклад силы сопротивления в ускорение снаряда. Его можно сильно упростить, если вспомнить, что снаряд — шар

Первая формула — масса шара, и тут — плотность материала, из которого сделано ядро, а r — радиус ядра. Вторая формула — площадь поперечного сечения шара. Подставим эти формулы в выражение для коэффициента и упростим

где d — диаметр ядра, калибр нашей пушки. Из этой формулы уже видно, что чем больше будет калибр и плотнее материал снаряда, тем меньше будет влияние силы сопротивления воздуха.

Зададимся значениями параметров снаряда. Добавим в конец файла ballistics.m следующие строки

Пускай ядро будет чугунным калибра 100 мм. Что за слово такое, global перед каждой из переменных. Таким образом мы говорим системе, что созданные переменные будут доступны для всех скриптов и определенных в них функций, то есть будут глобальными.

Остается записать для Octave построенную нами модель в виде функции, пусть это будет функция f_air. Естественно, для неё нужно создать отдельный файл f_air.m. Попробуйте провернуть это самостоятельно. Дам подсказку: начале тела этой функции следует определить ещё раз наши глобальные параметры снаряда, но уже без значений. Это необходимо, чтобы функция видела глобальные переменные

Если будут совсем трудно, загляните под спойлер.

С приведением к форме Коши всё просто. Вот исходная система уравнений

Первые производные координат есть проекции скорости

что дает систему уравнений

Теперь решаем систему уравнений движения, в файле ballistics.m даем команды

то есть интегрируем новые уравнения движения с теми же начальными условиями и на том же временном интервале, что и для задачи без учета сопротивления воздуха, а так же рисуем график траектории

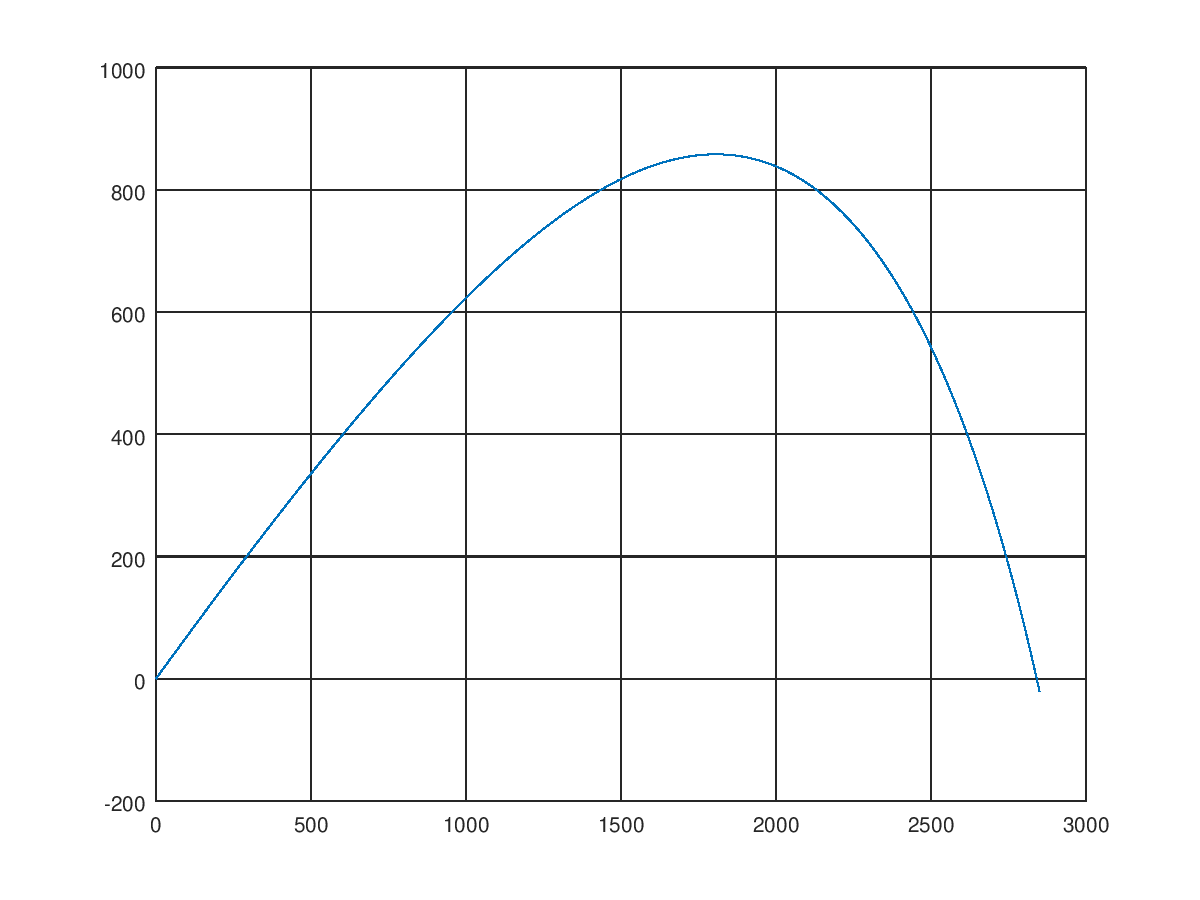
Ого, максимальная высота полета уменьшилась весьма существенно. И 47 секунд теперь слишком большой диапазон, снаряд падает на землю намного раньше. Поиграем со временем

При tend = 26 секунды видим, что и дальность полета весьма значительно. Видно, что аэродинамическое сопротивление очень существенно влияет на характеристики нашего орудия и в реальности пренебрегать им нельзя. Меняется и форма траектории: она более полога на восходящем участке, и круто идет вниз на нисходящем, мало напоминая идеальную параболу.

5. Сравнение траекторий снаряда

Мы уже видим, что результаты моделирования полета ядра различаются между собой. Но всё познается в наглядном сравнении. Построим две траектории одновременно. Можно? Да проще простого

Сначала мы указали абсциссу и ординату для одной траектории, потом для другой. Что получилось?

Эмм, это какой-то бред. Правильно, время полета снаряда в разных решениях разное. Столкновение ядра с поверхностью мы не моделируем. Из этой ситуации можно выкрутится, задав пределы изменения координат по осям командной axis(), вот так

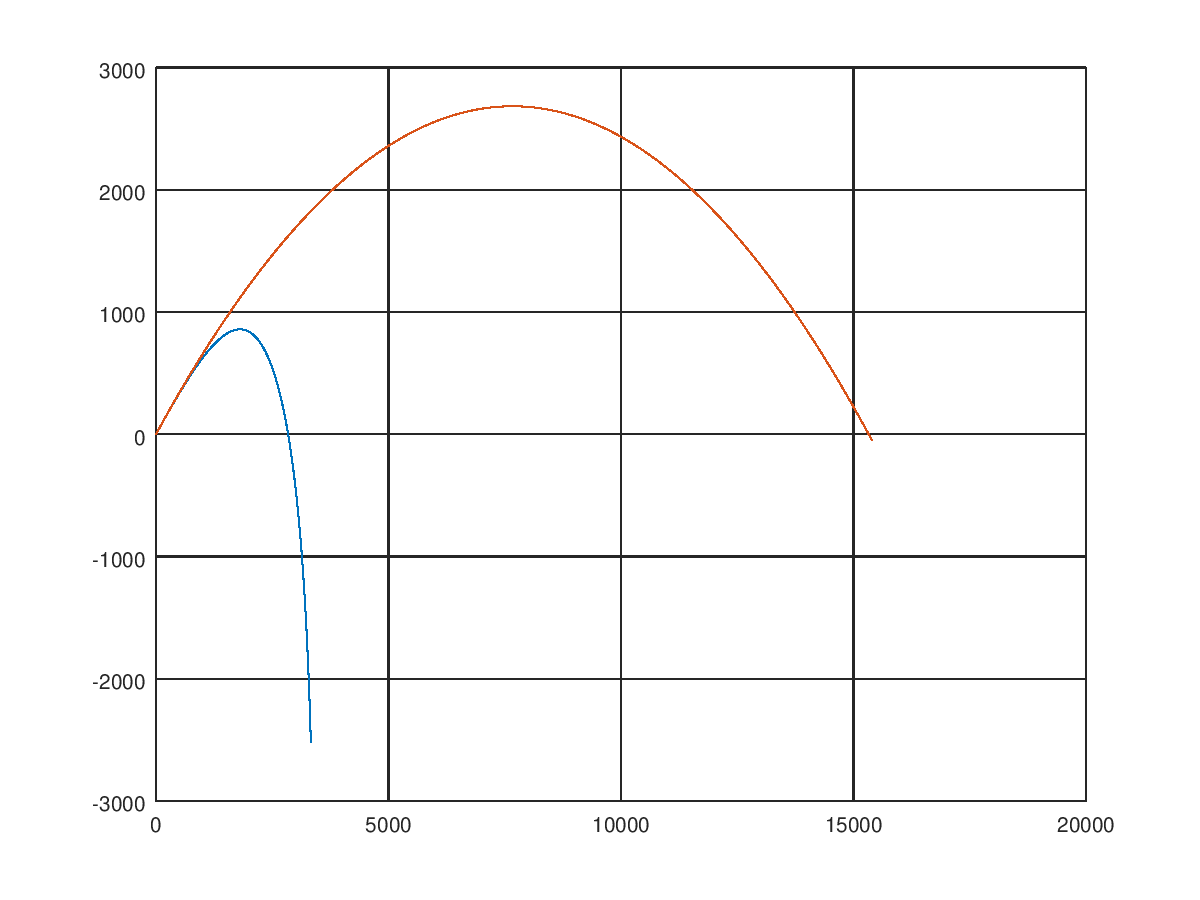
Теперь графики будут выглядеть так

Уже лучше. По крайней мере траектории можно сравнить между собой. А если нам хочется, чтобы по всем осям графика был одинаковый масштаб? Гугление дало такую команду

определяющий одинаковый масштаб осей графика по всем осям координат

Под спойлером полный текст файла ballistics.m

Заключение

В рассмотренном нами примере мы столкнулись с фундаментальным свойством законов природы — они нелинейны. Если учитывать сопротивление воздуха, то правые в части дифференциальных уравнений фазовые координаты входят нелинейно. Аналитического решения, то есть выраженного в элементарных функциях задача не имеет. Наличие аналитического решения для реальных задач техники скорее исключение. И без моделирования при их решении уже никак не обойтись.

Но само по себе решение уравнений движения на практике имеет мало смысла. Что нам дало это решение? Да, мы увидели влияние силы сопротивления воздуха на полет пушечного ядра. Но мы, например, не ответили на многие вопросы, например, какова точная дальность стрельбы нашей пушки? Какова максимальная высота подъема снаряда? Под каким углом надо стрелять, чтобы достичь максимальной дальности?

Математические модели создают для того, чтобы решать с помощью них практические задачи техники. Вот об этом мы и поговорим в следующий раз.

Колебания материальной точки в теоретической механике

Содержание:

Колебания материальной точки:

К исследованию колебаний одной материальной точки могут быть сведены многие технические задачи

В качестве примера интегрирования дифференциальных уравнений движения рассмотрим колебания материальной точки. Еще совсем недавно изучение колебаний не входило в программу курсов теоретической механики высших учебных заведений. Но необходимость создания новых методов расчета всевозможных машин и различных сооружений, обладающих большой прочностью при небольшом весе, а также необходимость увеличения скоростей и производигельности машин стимулировали быстрое развитие раздела динамики, называемого теорией колебаний. Раздел, посвященный колебаниям, включен теперь во все программы по теоретической механике.

C основами явлений колебаний удобно ознакомиться сперва на примере, колебания одной материальной точки. Изучение вибраций одной материальной точки интересно также и потому, что к вибрации точки могут быть непосредственно приведены многие практически важные задачи.

Пусть точка M массы m притягивается к точке О силой F, пропорциональной (рис. 162) расстоянию ОМ, а начальная скорость точки M направлена по прямой OM или равна нулю. В таком случае точка M будет двигаться по прямолинейной траектории, вдоль которой мы направим ось х. Начало координат возьмем в точке О (в равновесном положении). Сила F как бы стремится вернуть точку M в равновесное положение О, за что ее называют восстанавливающей силой. Примером такой силы могут служить сила упругости стержня, совершающего малые колебания, или равнодействующая сил веса G и натяжения T нити при малых колебаниях маятника и т. и. Чем больше координата х, тем больше величина этой силы. Вместе с тем сила (точнее говоря, ее проекция на ось Ох) по знаку всегда противоположна знаку координаты х. В самом деле, если точка M находится справа от x начала координат О, то координата х положительна, а сила направлена в отрицательную сторону, и наоборот, если координата х отрицательна, то восстанавливающая сила направлена в положительную сторону. Обозначив коэффициент пропорциональности между силой и расстоянием через с (причем с > 0), выразим восстанавливающую силу формулой

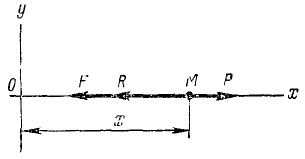
Рис. 162

Пусть на точку M во время ее движения действует сила сопротивления R, пропорциональная скорости точки и направленная против скорости. Таким образом, если точка M движется вправо (х > 0), то сила сопротивления направлена влево (R 0. Обозначив коэффициент пропорциональности через а (причем а > 0), мы определим силу сопротивления (выражаясь точнее, ее проекцию на ось Ох) формулой

Кроме того, пусть на точку M действует возмущающая сила Р, т. е. некоторая дополнительная сила, вызывающая изменение движения, обусловленного основной силой F. Возмущающая сила направлена по прямолинейной траектории точки M и, периодически изменяя свою величину и знак, раскачивает точку M то в ту, то в другую сторону. Мы ограничимся рассмотрением простейшего случая и предположим, что сила P изменяется с течением времени по закону синуса:

P = H sin pt. (133)

Очевидно, что сила P изменяется в пределах от +Н до —Н. Пример такой силы приведен в задаче № 110.

Напишем дифференциальное уравнение движения точки M:

Разделив обе части уравнения на т, введем обозначения

(134)

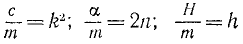
и перенесем члены, содержащие х или его производные, влево:

х + 2nx + k 2 x =h sin pt. (135)

Мы имеем неоднородное линейное дифференциальное уравнение с постоянными коэффициентами. Общее решение такого уравнения складывается из: 1) общего решения соответствующего однородного уравнения, т. е. уравнения (135) без правой части, и какого-либо частного решения неоднородного уравнения (135).

Для интегрирования уравнения

х + 2nx + k 2 x = 0

составим характеристическое уравнение

z 2 + 2nz + k 2 = 0.

Если n 2 sin (pt— δ)

и подставим в (135) написанное выражение х и его производных:

— Bp 2 sin (pt — δ) + 2nBp cos (pt — δ) + k 2 B sin (pt — δ) = h sin pt.

Преобразуем правую часть этого равенства:

h sin pt = h sin (pt — δ +δ) = h sin (pt — δ) cos ∂ + h cos (pt — δ) sin δ.

Перенеся все члены влево и собирая члены, содержащие sin(pt— δ) и cos (pt — δ), получим

[В (k 2 —p 2 )-h cos δ] sin (pt — δ) + (2Bnp-hsin δ) cos (pt — δ) = O.

Это равенство обращается в тождество, если

В (k 2 — р 2 ) = h cos δ; 2Bnp = h sin δ,

(137)

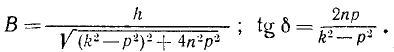
Складывая общее решение (136) однородного уравнения с найденным частным решением неоднородного уравнения, получим общее решение неоднородного уравнения (135) в таком виде:

(138)

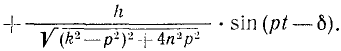
Прежде чем исследовать сложное колебательное движение точки под действием сил F, R и P, выражаемое уравнением (138), рассмотрим более простые движения, которые точка совершала’ бы под действием одной силы F или же под действием силы F и какой-либо- одной из двух остальных R или Р.

Точка, движущаяся по прямой, совершает под действием восстанавливающей силы гармоническое колебание

Свободные колебания без сопротивления

Предположим, что на материальную точку M (см. рис. 162 на стр. 274) действует только восстанавливающая сила (131), сила же сопротивления (132) и возмущающая сила (133) равны нулю. Пусть начальная скорость точки M направлена по прямой MO или равна нулю. В таком случае точка M будет двигаться по прямой OM (по оси Ох), дифференциальное и кинематическое уравнения ее движения мы получим, положив в (135) и в (138) n и h равными нулю. В самом деле, если сила сопротивления R=O, то, следовательно, α = 0, потому что R=— ах и х переменная величина. Если же a = 0, то равно нулю и n, которое согласно (134) равно 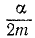. Аналогично, равенство нулю возмущающей силы означает, что равны нулю H и h.

В таком случае уравнение (135) принимает вид

Этому уравнению придадим более удобный вид, для чего выразим, постоянные интегрирования C₁ и C₂ через две другие постоянные величины А и β, однозначно связанные с C₁ и C₂ соотношениями

x = A sin (kt+ β). (140)

Это уравнение является одним из важнейших уравнений в теории колебаний и описывает наиболее простое колебательное движение, называемое гармоническим. Еще в древности было известно, что если некоторая точка M’ (рис. 163) равномерно движется по окружности радиуса О’М’ — А со скоростью kA, то проекция M этой точки на какую-либо ось Ох, лежащую в плоскости окружности, совершает гармонические колебания. Мы воспользуемся рис. 163, чтобы нагляднее ознакомить читателя с параметрами гармонического колебания.

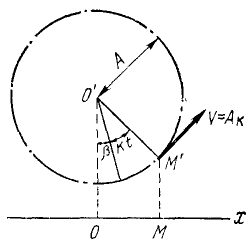
Рис. 163

Если точка M’ опишет полную окружность, то точка M’ совершит одно полное колебание.

Время одного полного колебания точки M (или, что то же, время,в течение которого точка M’ описывает одну полную окружность) называют периодом -τ₀ колебаний.

Угловая скорость k, с которой поворачивается радиус-вектор 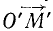при равномерном движении точки M’, равна циклической, круговой или угловой частоте колебаний точки М. Эту величину обычно коротко называют частотой, хотя, как будет видно из дальнейшего, оба понятия не вполне идентичны.

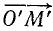
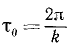
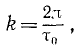
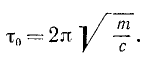
Период и угловая частота связаны простым соотношением, которое становится очевидным, если учесть, что τ₀—это время, в течение которого , вращаясь с угловой скоростью k, поворачивается на 2π:

и (141)

(142)

Период имеет размерность времени

Частота имеет размерность угловой скорости

Из (141) видно, что круговая частота k равна числу полных колебаний, совершаемых в 2π сек. Частота ν колебаний пропорциональна круговой (циклической, угловой) частоте k и равна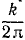. В технике и в физике частоту обычно измеряют в герцах (гц). 1 гц — частота, равная одному полному колебанию (циклу) в секунду. Иначе говоря, герц есть частота такого периодического процесса, который повторяется каждую секунду. Обратите внимание на то, что частота и период гармонических колебаний зависят от массы точки и коэффициента с восстанавливающей силы и не зависят от начальных данных.

Максимальное отклонение А точки M от среднего (равновесного) положения О в ту или в другую сторону (или, что то же, радиус круговой траектории точки М’) называют амплитудой. Амплитуду измеряют в единицах длины:

Аргумент синуса (kt + β) называют фазой колебания, a β—начальной фазой. Физический смысл фазы колебания выявляется при сравнении двух колебаний с одинаковыми частотами, но с разными начальными фазами. Колебание с фазой (kt+ β) опережает колебание с фазой kt, а колебание с фазой (kt — β) отстает от него (разумеется, при положительном β).

Напомним, что А и β являются постоянными интеграции, а следовательно, их определяют по начальным данным. Пусть в начальное мгновение t = 0, x=x₀ и x=x₀. Продифференцировав (140) по времени, получим х = Ak cos (kt + β), и подставляя начальные значения:

(143)

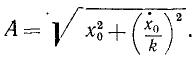
Из тех же равенств можно определить и начальную фазу 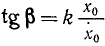. Амплитуда и начальная фаза зависят от частоты и от начальных данных.

Задача №1

Груз весом 2 T подвешен на тросе (рис. 164). При равномерном спуске груза со скоростью υ = 5м/сек произошла неожиданная задержка верхнего конца троса вследствие защемления троса в обойме блока. Пренебрегая весом троса, определить его наибольшее натяжение при последующих колебаниях груза, если коэффициент жесткости троса с = 4 T/см.

Решение. Примем следующие единицы измерений: длина—в см, время — в сек, сила—в Т. Рассмотрим движение груза. На груз действуют две силы: вертикально вниз вес груза 2T, вертикально вверх — натяжение троса. Груз спускался равномерно, следовательно, до защемления натяжение троса равнялось весу груза. В этом равновесном положении его застала авария. После защемления троса груз не остановился мгновенно. В это мгновение он имел скорость 5 м/сек и продолжал опускаться. Но по мере опускания груза сила натяжения троса возрастала от своего начального значения 2T. Ускорение груза направлено по силе и пропорционально ей. Поэтому опускание груза было замедленным и в некоторое мгновение скорость груза, перейдя через нуль, стала направленной вверх, в направлении силы и ускорения. Движение вверх было ускоренным, но по мере того как груз поднимался, растяжение троса, а следовательно, и его натяжение уменьшались, а потому уменьшалось ускорение груза, скорость же продолжала увеличиваться до момента прохождения через равновесное положение. После этого груз, набрав скорость, продолжал подниматься, ио замедленно, так как натяжение троса стало меньше силы веса и равнодействующая приложенных к грузу сил была направлена вниз. Затем скорость стала равной нулю, груз начал падать вниз, натяжение троса возрастало и движение повторялось снова неопределенное количество раз.

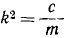
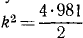
Начало О системы отсчета выберем обязательно в равновесном положении груза, относительно которого происходят колебания, направив ось Ox вертикально вниз (рис. 164). В начальное мгновение (в момент защемления троса) было: x₀= 0; x₀= 500 см/сек. Квадрат круговой частоты определим по (134). После подстановки в формулу имеем . Определим амплитуду по формуле (143):

Таким образом, при равновесном положении груза натяжение троса равно 2T; когда же груз опустился на одну амплитуду, то трос растянулся еще на 11,28 см, а при жесткости троса в 4 T/см натяжение его увеличилось еще на 45,12 Т.

Натуральный логарифм отношения двух последующих амплитуд затухающих колебаний называют логарифмическим декрементом

Свободные колебания с сопротивлением

Движение под действием восстанавливающей силы и силы сопротивления будем называть свободными колебаниями. Мы только что убедились, что свободные колебания без сопротивления являются гармоническими и, раз возникнув, они повторялись бы до тех пор, пока их не прекратила бы или не изменила бы какая-нибудь внешняя сила. Пусть возмущающая сила отсутствует (P = 0, H = 0, h = 0), а на точку действуют силы F=-cx и R =—ах. Дифференциальное уравнение (135) движения точки M принимает вид

х + 2nx 4- k 2 x = 0, (144)

а его интеграл получим, положив в (138) h=0:

или, если воспользуемся соотношениями (140),

(145)

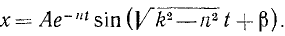
Постоянные А и β определяют по начальным данным.

Наиболее существенное отличие уравнения (145) от уравнения (140), иначе говоря, наиболее существенное изменение в свободном колебании точки М, внесенное наличием силы сопротивления, заключается в множителе e -nt , который с течением времени непрерывно уменьшается, вследствие чего амплитуда Ae -nt колебаний с сопротивлением убывает по экспоненциальному закону, асимптотически приближаясь к нулю. Такое колебание называют затухающим.

Переходя к определению периода затухающих колебаний, обратим внимание на то, что вообще периодом периодического движения называют промежуток времени между двумя последовательными прохождениями точки (или системы) через одно и то же положение водном и том же направлении. В случае затухающих колебаний только равновесное положение удовлетворяет такому определению периода, через всякое же другое положение точка M (или любая система, совершающая затухающие колебания) проходит через неравные промежутки времени (см. рис. 165). Поэтому под периодом затухающих колебаний понимают промежуток времени τ₁ между двумя последовательными прохождениями точки M (или системы) через положение равновесия в одинаковом направлении. В таком же смысле колебания, описываемые уравнением (145), могут быть названы изохронными. Период затухающих колебаний можно определить но формуле

(146)

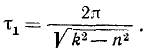
Проф. И. М. Бабаков в учебнике «Теория колебаний» рекомендует для практических расчетов более удобную формулу:

(146 / )

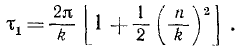
Сравнивая (141) и (146), мы видим, что сопротивление увеличивает период свободных колебаний, но незначительно.

Гораздо больше оно влияет на убывание амплитуд. Так, например, при n = 0,05 k сопротивления увеличивают период на 0,125%, а амплитуда за время одного полного колебания уменьшается более чем на 25%. На рис. 165 изображен график затухающих колебаний для случая n = 0,05 k, позаимствованный из «Лекций» проф. Е. Л. Николаи.

Отношение абсолютных значений двух последовательных амплитудных отклонений точки от равновесного положения называют коэффициентом затухания:

(147)

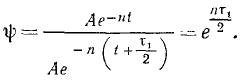
Для характеристики быстроты убывания амплитуды удобнее пользоваться натуральным логарифмом коэффициента затухания, называемым логарифмическим декрементом колебаний:

(147 / )

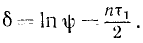
На рис. 165 пунктиром изображены кривые, уравнения которых x= Ае -n и х = —Ae -nt . График затухающих колебаний расположен между этими двумя кривыми и поочередно их касается.

Задача №2

Маятник, масса которого равна 1 кг и период качания в безвоздушной среде τ₀=l сек, заставили качаться вереде, сопротивляющейся но закону R =—2х н. Определить: 1) период затухающих колебаний маятника и 2) уменьшение амплитуды в течение трех периодов.

Решение. Определим параметры колебаний.

Круговая частота. Период τ₀=l сек= 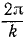, откуда k=2π = G,28.

Коэффициент α=2; m=1; 2n=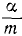, откуда n=l.

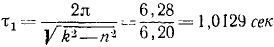
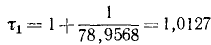
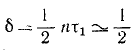
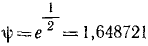
Период затухающих колебаний , или по (146′),
. Логарифмический декремент . Коэффициент затухания .

Отношение каждого максимального отклонения к последующему (через полпериода) равно коэффициенту затухания, следовательно, если амплитуду при первом размахе принять за 1, то следующие уменьшаются в отношении .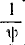

Под действием восстанавливающей и возмущающей сил точка совершает сложное колебание, являющееся результатом наложения трех гармонических колебаний: свободного, сопровождающего свободного и вынужденного

Вынужденные колебания без сопротивления

Пусть на точку М, движущуюся по оси Ох, действуют две силы — восстанавливающая F=— CX и возмущающая P =H sin pt, направленные также по оси Ох. Величина pt может быть названа фазой силы, постоянную р назовем круговой частотой возмущающей силы, а период этих изменений обозначим через τ. Действие сопротивления мы пока не учитываем, поэтому, положив в уравнении (135) n = 0, получим следующее дифференциальное уравнение вынужденных колебаний без сопротивления:

x+ k 2 x = h sin pt. (148)

Чтобы найти решение этого уравнения, надо в (138) положить равным нулю не только n, но и δ, так как согласно (137) δ = 0 при n = 0. Имеем

Определим постоянные. Если в начальное мгновение х = x₀ и x = χ₀, то

(149)

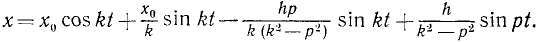
Первые два слагаемых описывают свободные колебания с частотой k. Воспользовавшись соотношениями (140″), эти два слагаемых можно представить в виде x₁ = A sin (kt + β). Если в начальное мгновение х = х= 0, то эти колебания во все время действия возмущающей силы не возникают. Третье слагаемое

— гармоническое колебание, происходящее с частотой k свободных колебаний, но с амплитудой, зависящей от возмущающей силы. Это колебание всегда, при любых начальных условиях, сопровождает вынужденные колебания и его называют свободным сопровождающим колебанием. Четвертое слагаемое

(149 / )

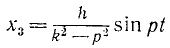
описывает вынужденные колебания. Таким образом, колебания точки являются результатом линейного наложения трех гармонических колебаний: 1) свободных, 2) сопровождающих свободных и 3) вынужденных (рис. 166):

(149 // )

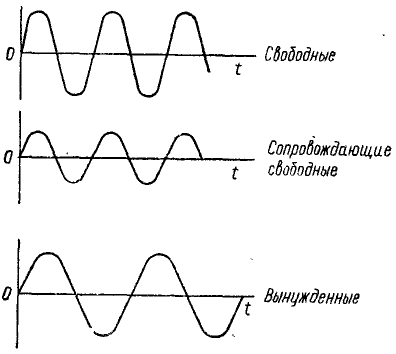
Рис. 166

На схеме (рис. 166) приведены только частоты этих колебаний, но разумеется, не изображены амплитуды и начальные фазы.

Вынужденные колебания происходят с частотой р, равной частоте возмущающей силы. Они не зависят от начальных данных.

Как видно из (143), для изменения амплитуды свободных колебаний достаточно изменить начальное отклонение или начальную скорость. Напротив, для изменения амплитуды вынужденных колебаний надо изменить возмущающую силу, что обычно бывает сопряжено с необходимостью преобразования конструкции.

Если частота р вынужденных колебаний меньше частоты k собственных (случай «малой» частоты), то амплитуда вынужденных колебаний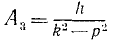, а фаза pt вынужденных колебаний совпадет
с фазой pt возмущающей силы. По если р > k (случай «большой» частоты), то выражение, написанное для А₃, становится отрицательным, однако амплитуда не может быть отрицательной. Это кажущееся несоответствие объясняется тем, что при р > k фаза вынужденных колебаний противоположна фазе возмущающей силы и уравнение вынужденных колебаний имеет вид

Резонанс

Если частоты собственных и вынужденных колебаний близки между собой, то амплитуды получаются очень большими. Напомним, что при интегрировании уравнения (135) мы положили p≠k. Если р= k, то дифференциальное уравнение (148) имеет вид

x-k 2 x = h sin kt (148′)

Будем искать частное решение вида

Определив х =— 2Bk sin kt— Btk 2 cos kt и подставив его вместе с х в дифференциальное уравнение, получим
— 2Bk sin kt = h sin kt,

Находим общее решение дифференциального уравнения движения:

Дифференцируем по времени:

Если в начальное мгновение x=x₀ и x=x₀, то

и общее решение принимает вид

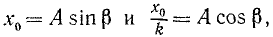
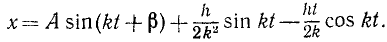
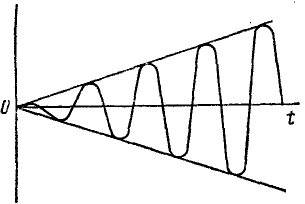
или, полагая получим

(148»’)

Следовательно, и при равенстве частот движение точки состоит из трех колебательных движений, однако вынужденные колебания представлены непериодическим членом, в коэффициент которого входит множителем время. C течением времени это третье слагаемое, называемое вековым членом, безгранично растет по абсолютной величине. Размах вынужденных колебаний непрерывно растет по линейному закону. Это явление называется резонансом. График вынужденных колебаний при резонансе представлен на рис. 167.

Задача №3

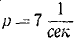
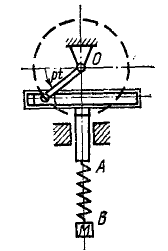
Груз M подвешен в точке В к пружине AB (рис. 168), верхний конец А которой прикреплен к поступательно движущейся кулисе. Кривошип кулисного механизма имеет длину а = 0,02 м и вращается с угловой скоростью , вследствие чего точка А совершает гармонические колебания по закону х_А =0,02 sin 7t м. Определить вынужденные колебания груза М, если его вес G = 3,6 н, а жесткость пружины с = 36 н/м.

Рис. 168

Решение. Составим дифференциальное уравнение движения груза М. Начало координат выберем в точке, с которой центр тяжести груза совладал в момент начала движения (при t = 0), когда верхний конец А пружины, совершающей гармонические колебания вместе с кулисой, занимал свое среднее положение. При сделанном нами выборе начала отсчета (в равновесном положении груза) вес G = 3,6 н уравновешивался статическим натяжением пружины с λ_cr = 36 ∙ 0,1. Наличие этих двух взаимно уравновешенных сил эквивалентно их отсутствию, а потому мы можем их отбросить и в дальнейшем рассматривать движение центра тяжести груза лишь под действием натяжения пружины, обусловленного только ее динамической деформацией, т. е. только деформацией пружины при колебании груза около равновесного положения.

При t ≠ 0 положение центра тяжести груза определяется координатой х, получающейся от суммирования двух перемещений: динамической деформации пружины и перемещения a sin pt верхнего конца А пружины. Следовательно, динамическая деформация пружины равна разности перемещений ее нижнего конца В и верхнего конца А, т. е. равна х—α sin pt . Дифференциальное уравнение движения центра груза имеет вид

mx = — с (х—a sin pt).

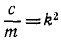
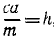
Деля обе части уравнения на m и вводя обозначения и , придадим этому уравнению знакомый нам вид (148)

x + k 2 x = h sin pt,

где

Подставляя в (149′), находим вынужденные колебания груза.
Ответ. 0,04 sin 7t.

Задача №4

Статический прогиб рессор товарного вагона равен 5 см. Определить критическую скорость вагона, при которой начнется «галопирование» вагона, если на стыках рельсов вагон испытывает толчки, вызывающие вынужденные колебания на рессорах: длина рельсов равна 12 м.

Решение. Жесткость рессор 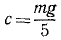, частота собственных колебаний

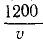
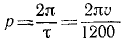
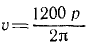
Если поезд идет со скоростью υ см/сек, то вагон получает толчки на стыках через каждые сек. Таков период τ возмущающей силы. Частота возмущающей силы , откуда . Галопирование вагона произойдет при резонансе, т. е. при равенстве частот собственных и вынужденных колебаний. Подставляя в выражение, полученное для скорости, р = k = 14, найдем

Чтобы выразить скорость в км/ч, умножим выраженную в см/ceκ скорость на 0,036.

Если к точке приложены восстанавливающая и возмущающая сила и сила сопротивления, то свободные колебания затухают и остаются только вынужденные

Влияние сопротивления на вынужденные колебания

Если на точку, кроме восстанавливающей и возмущающей сил, действует также и сила R сопротивления, то движение точки описывается дифференциальным уравнением (135) и его решением (138).

Первый член правой части (138) с возрастанием t стремится к нулю, и соответствующие ему колебания точки с течением времени затухают, поэтому ими можно пренебречь. Остаются только вынужденные колебания (рис. 169):

(150)

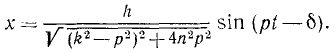
Они происходят с частотой возмущающей силы, сопротивление не влияет на период вынужденных колебаний. Амплитуда не зависит от начальных условий и времени и не изменяется с течением времени.

Предположим, что возмущающая сила сохраняет свое максимальное значение Н. При равновесии под действием такой силы и восстанавливающей силы F =— сх точка M получила бы так называемое статическое отклонение

Из этого соотношения найдем максимальное ускорение точки M под действием возмущающей силы: h=k 2 x_ст и, подставляя это значение h в выражение (150), выразим амплитуду вынужденных колебаний равенством

Отношение частоты вынужденных колебаний к частоте собственных колебаний

(151)

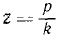
носит название коэффициента расстройки и отношение величины n, измеряемой в ceκ -1 , к частоте собственных колебаний называют безразмерным коэффициентом вязкости:

(151′)

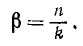
Введя эти обозначения в предыдущее равенство и разделив обе части его на x_ст, получим:

(152)

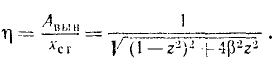
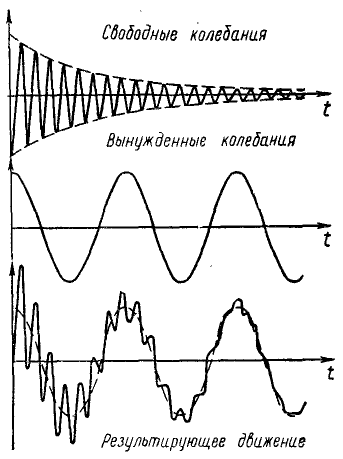
Рис. 169

Величина η—коэффициент динамичности — позволяет охарактеризовать динамический эффект, вызываемый возмущающей силой.

Коэффициент динамичности η зависит от двух величин (z и β).

Задавшись каким-либо значением β, и откладывая по оси абсцисс различные значения z, а по оси ординат—соответствующие значения коэффициента динамичности η, получим, так называемые, резонансные кривые. На рис. 170 изображены резонансные кривые для значений безразмерного коэффициента вязкости: 0,25, 0,15. и 0,10. Пунктиром нанесена уходящая в бесконечность при 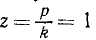резонансная кривая, соответствующая β = 0, т. е. вынужденным колебаниям без сопротивления.

Как показывает график (рис. 170) в областях, достаточно далеких от резонанса, амплитуды вынужденных колебаний с сопротивлением почти не зависят от безразмерного коэффициента вязкости. В этих областях при вычислении амплитуд вынужденных колебаний можно не учитывать сопротивлений и пользоваться более простой формулой

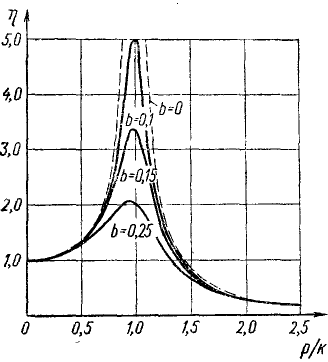
Рис. 170

При резонансе (р = k) амплитуда вынужденных колебаний при наличии сопротивлений остается конечной, но наибольшее значение амплитуда имеет, если 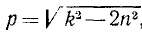, в чем легко убедиться, определив максимум амплитуды при различных р, считая h, k и п данными.

В вынужденных колебаниях с сопротивлением всегда бывает сдвиг фазы колебания по отношению к фазе .возмущающей силы. Величина этого сдвига определяется формулой (137).

Заметим, что все сказанное здесь относительно малых колебаний материальной точки полностью соответствует малым колебаниям материальной системы с одной степенью свободы.

• Количество движения
• Момент количества движения
• Мощность и работа силы
• Потенциальная энергия
• Естественный и векторный способы определения движения точки
• Координатный способ определения движения точки
• Касательное и нормальное ускорения точки
• Основные законы динамики

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.