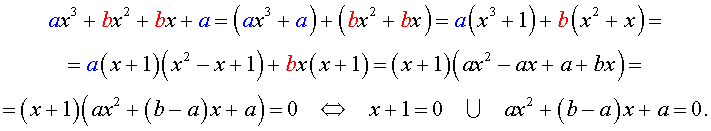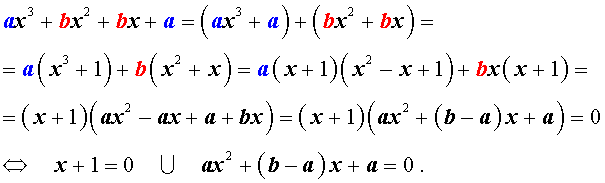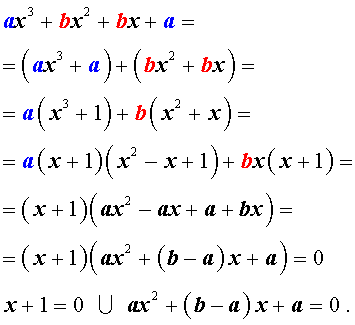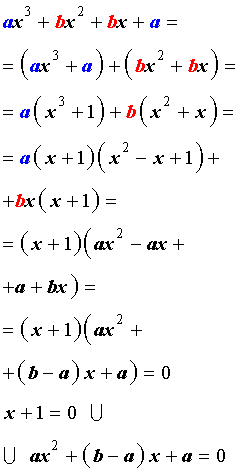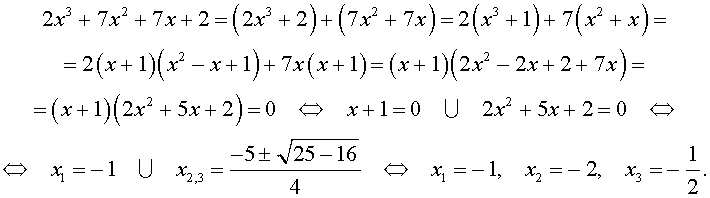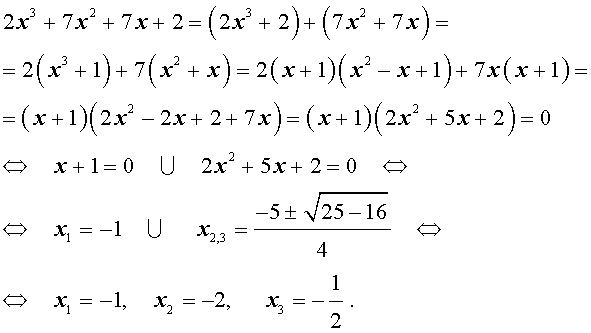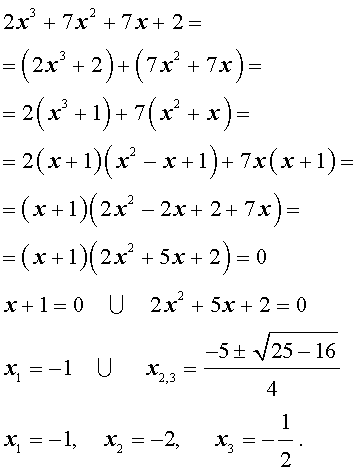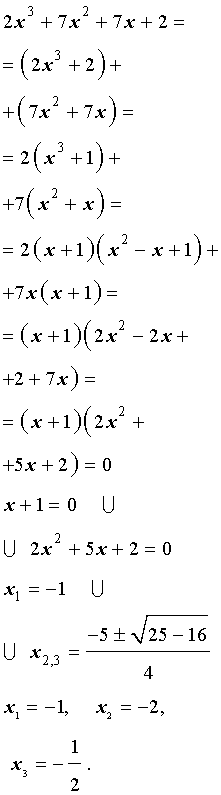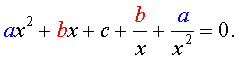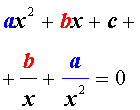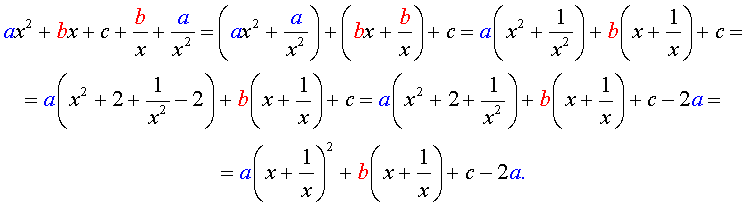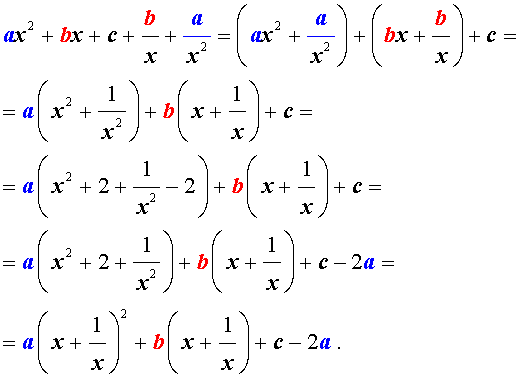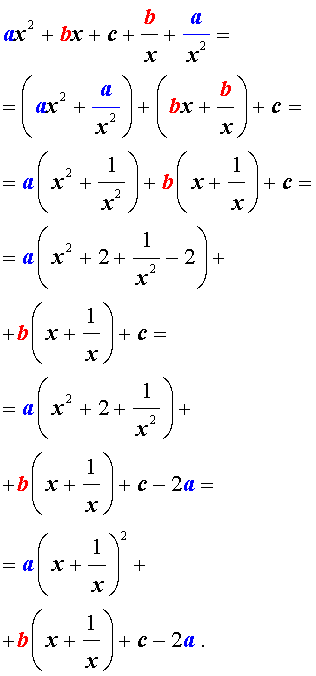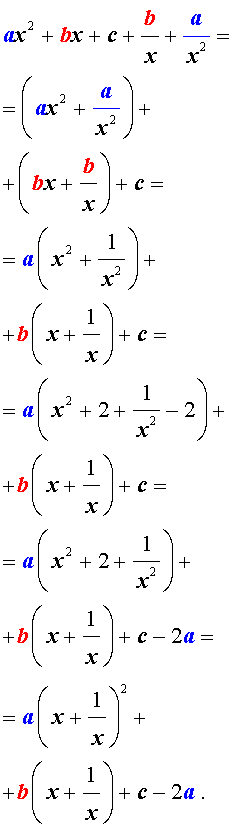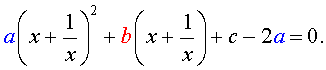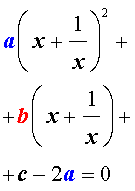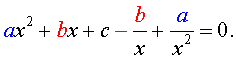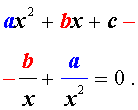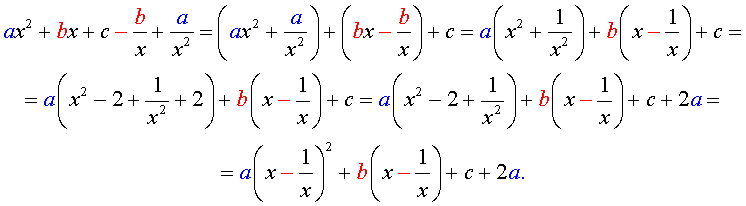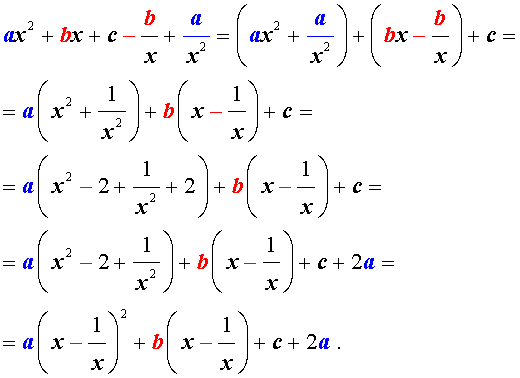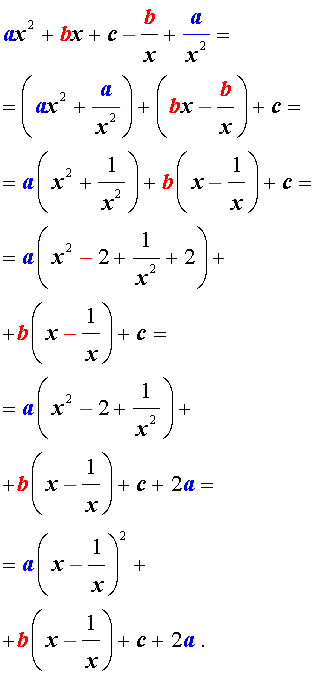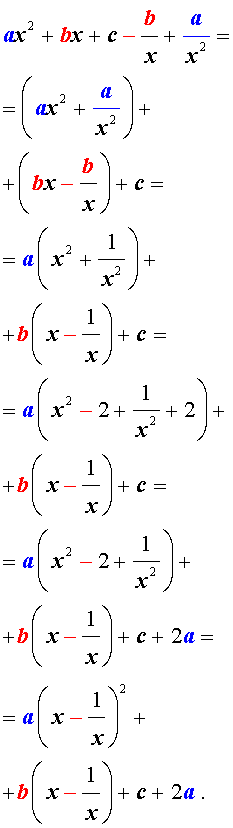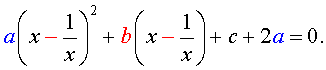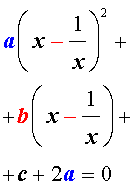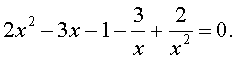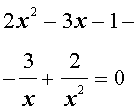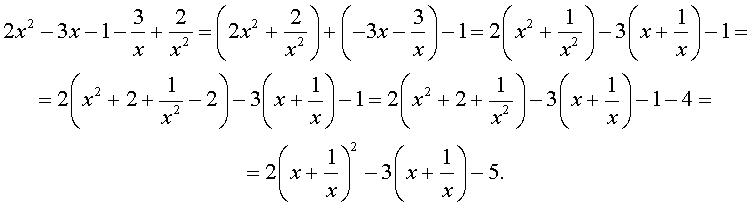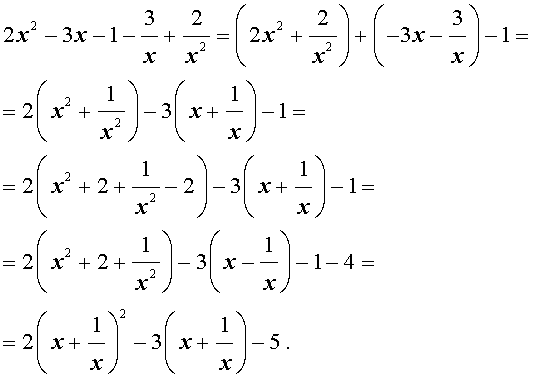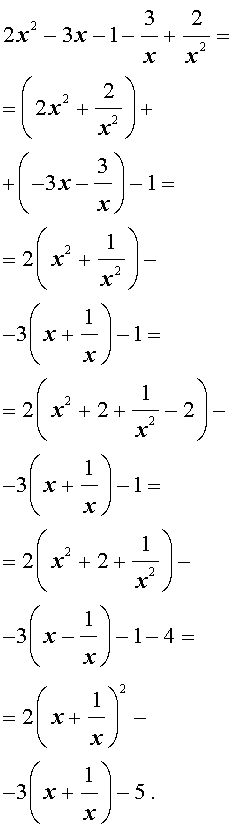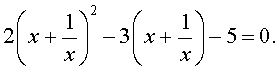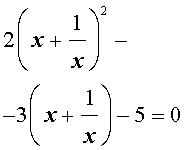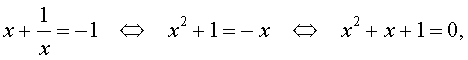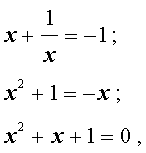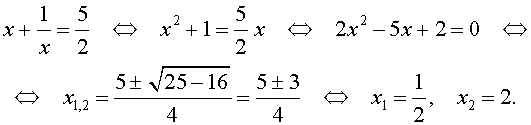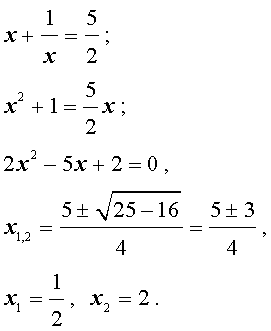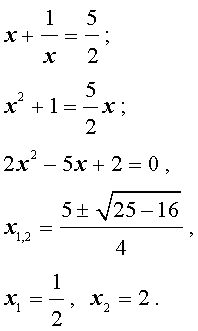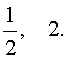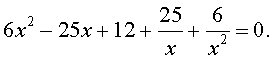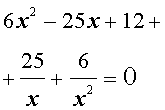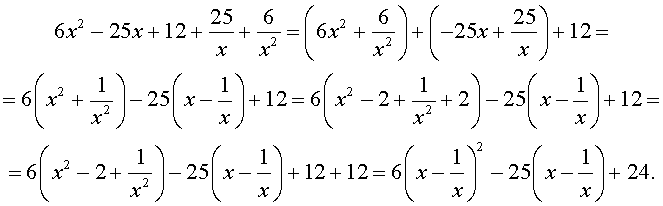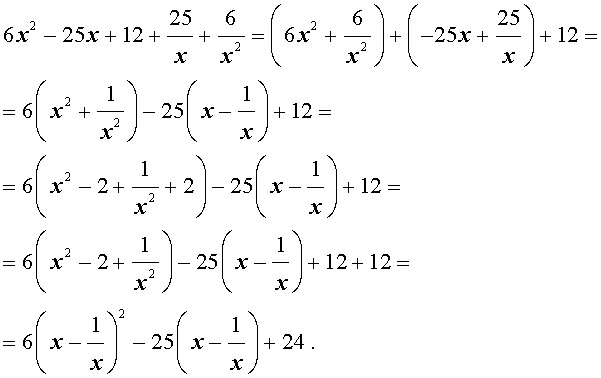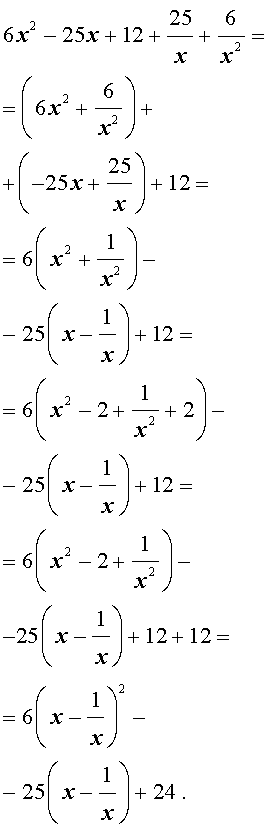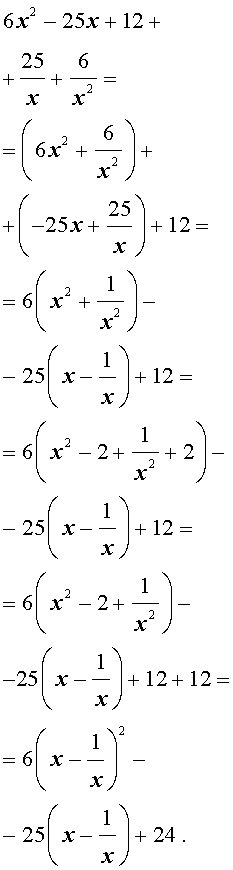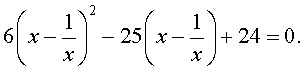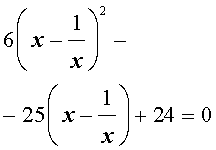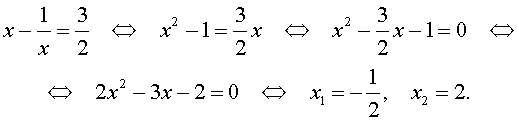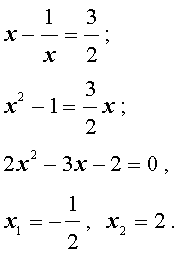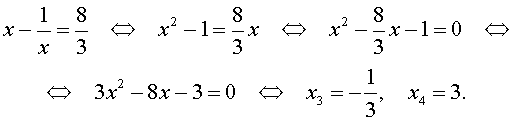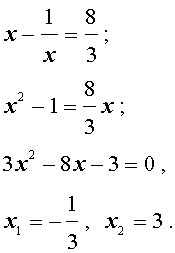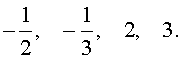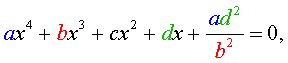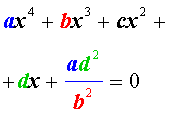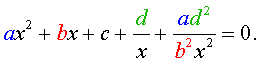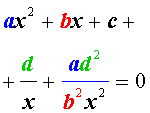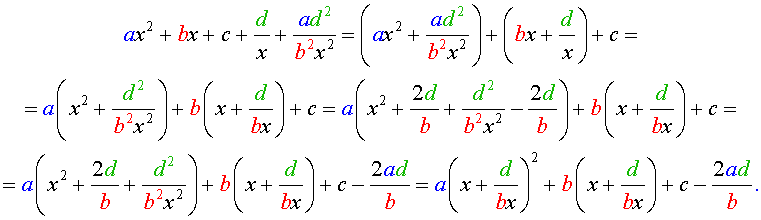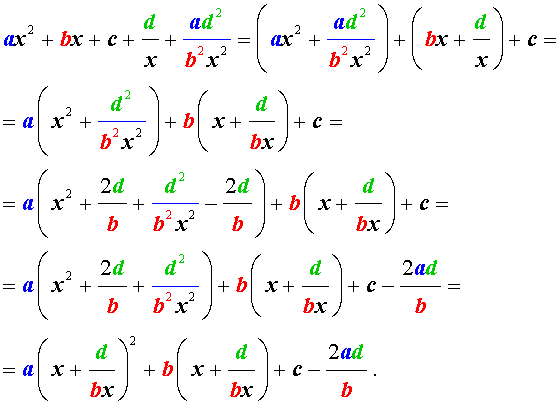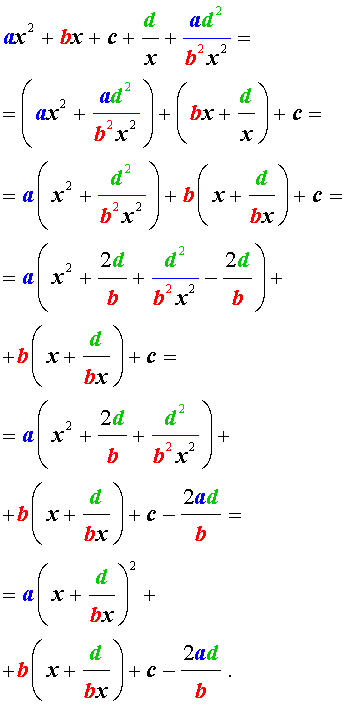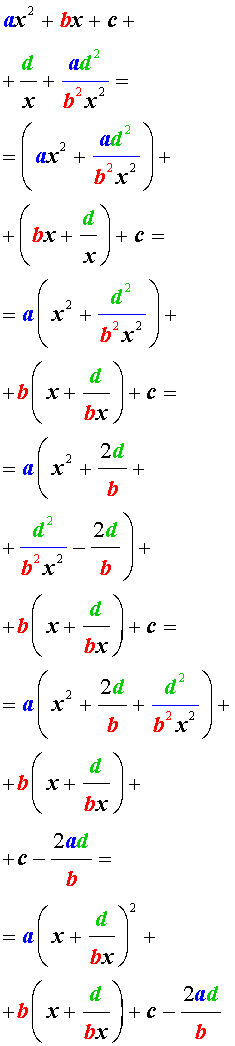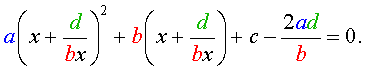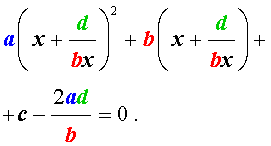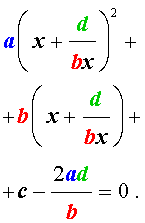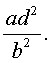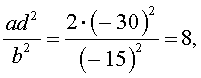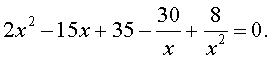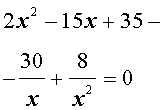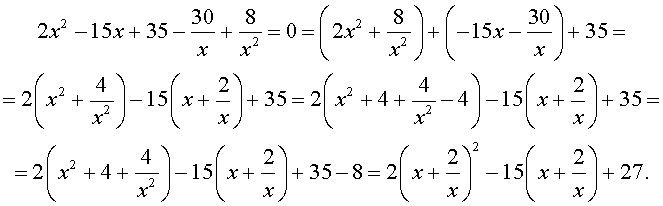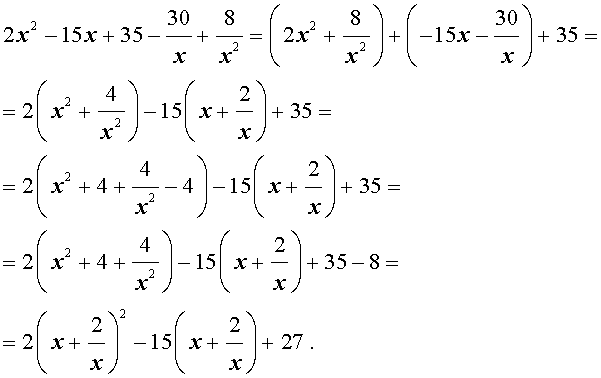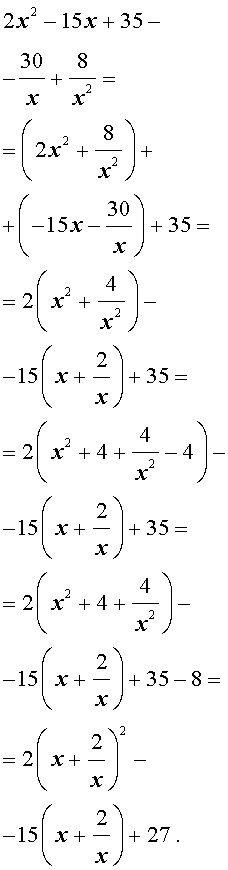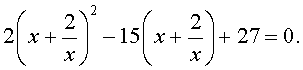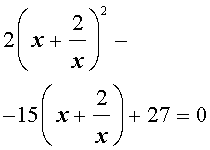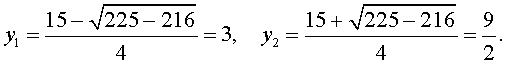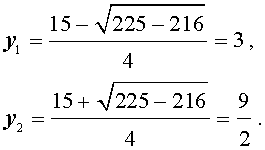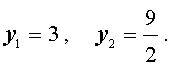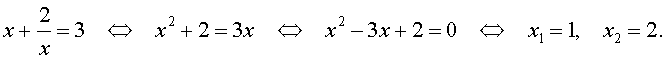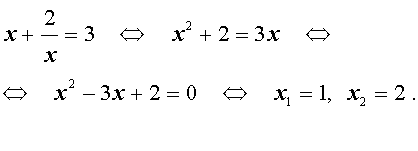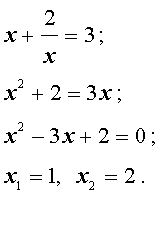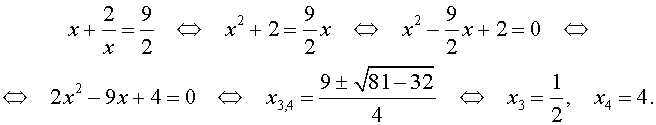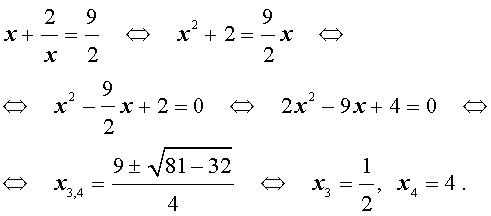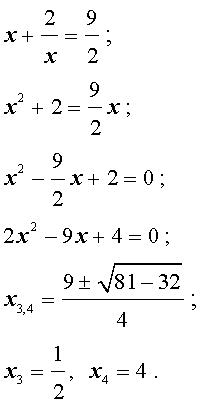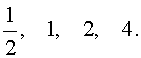Уравнения, сводящиеся к квадратным уравнениям:
возвратные (симметричные) уравнения
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
 | Трёхчленные уравнения |
 | Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии |
 | Возвратные (симметричные) уравнения 3-ей степени |
 | Возвратные (симметричные) уравнения 4-ой степени |
 | Обобщенные возвратные уравнения 4-ой степени |
Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .
Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| a x 3 + b x 2 + b x + a = 0, | (1) |
где a , b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
Пример 1 . Решить уравнение
| 2x 3 + 7x 2 + 7x + 2 = 0. | (2) |
Решение . Разложим левую часть уравнения (2) на множители:
Ответ :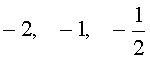
Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| a x 4 + b x 3 + cx 2 + + b x + a = 0, | (3) |
а также уравнения вида
| a x 4 + b x 3 + cx 2 – – b x + a = 0, | (4) |
Для того, чтобы решить возвратное уравнение (3), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
Если теперь обозначить
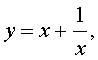 | (7) |
то уравнение (6) станет квадратным уравнением:
| a y 2 + b y + c – 2 a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
Если теперь обозначить
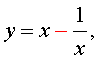 | (11) |
то уравнение (10) станет квадратным уравнением:
| a y 2 + b y + c + 2 a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (4) завершено.
Пример 2 . Решить уравнение
| 2x 4 – 3x 3 – x 2 – – 3x + 2 = 0. | (13) |
Решение . Уравнение (13) является возвратным и относится к виду (3). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
Если теперь обозначить
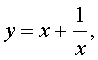 | (16) |
то уравнение (15) станет квадратным уравнением:
| 2y 2 – 3y – 5 = 0. | (17) |
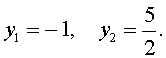 | (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ :
Пример 3 . Решить уравнение
| 6x 4 – 25x 3 + 12x 2 + + 25x + 6 = 0. | (19) |
Решение . Уравнение (19) является возвратным и относится к виду (4). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
Если теперь обозначить
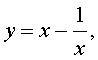 | (22) |
то уравнение (21) станет квадратным уравнением:
| 6y 2 – 25y + 24 = 0. | (23) |
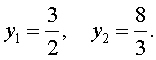 | (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ :
Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
где a , b , c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
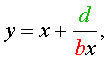 | (28) |
то уравнение (27) станет квадратным уравнением:
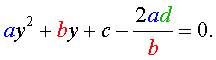 | (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (25) завершено.
Пример 4 . Решить уравнение
| 2x 4 – 15x 3 + 35x 2 – – 30 x + 8 = 0. | (30) |
Решение . Введем для коэффициентов уравнения (30) следующие обозначения
и найдем значение выражения
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
Если теперь обозначить
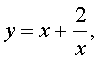 | (33) |
то уравнение (32) станет квадратным уравнением:
| 2y 2 – 15y + 27 = 0. | (34) |
В первом случае из равенства (33) получаем:
Во втором случае из равенства (33) получаем:
Ответ :
Симметрические системы уравнений и системы, содержащие однородные уравнения
Разделы: Математика
Цели урока:
- образовательная: обучение решению систем уравнений, содержащих однородное уравнение, симметрических систем уравнений;
- развивающая: развитие мышления, внимания, памяти, умения выделять главное;
- воспитательная: развитие коммуникативных навыков.
Тип урока: урок изучения нового материала.
Используемые технологии обучения:
Оборудование: компьютер, мультимедийный проектор.
За неделю до урока учащиеся получают темы творческих заданий (по вариантам).
I вариант. Симметрические системы уравнений. Способы решения.
II вариант. Системы, содержащие однородное уравнение. Способы решения.
Каждый ученик, используя дополнительную учебную литературу, должен найти соответствующий учебный материал, подобрать систему уравнений и решить её.
По одному учащемуся от каждого варианта создают мультимедийные презентации по теме творческого задания. Учитель при необходимости проводит консультации для учащихся.
Содержание урока
I. Мотивация учебной деятельности учащихся
Вступительное слово учителя
На предыдущем уроке мы рассматривали решение систем уравнений методом замены неизвестных. Общего правила выбора новых переменных не существует. Однако, можно выделить два вида систем уравнений, когда есть разумный выбор переменных:
- симметрические системы уравнений;
- системы уравнений, одно из которых однородное.
II. Изучение нового материала
Учащиеся II варианта отчитываются о проделанной домашней работе.
1. Демонстрация слайдов мультимедийной презентации «Системы, содержащие однородное уравнение» (презентация 1).
Учащиеся записывают в тетради:
2. Работа в парах учащихся, сидящих за одной партой: учащийся II варианта объясняет соседу по парте решение системы, содержащей однородное уравнение.
Отчёт учащихся I варианта.
1. Демонстрация слайдов мультимедийной презентации «Симметрические системы уравнений» (презентация 2).
Учащиеся записывают в тетради:
2. Работа в парах учащихся, сидящих за одной партой: учащийся I варианта объясняет соседу по парте решение симметрической системы уравнений.
III. Закрепление изученного материала
Работа в группах (в группу по 4 ученика объединяются учащиеся, сидящие за соседними партами).
Каждая из 6 групп выполняет следующее задание.
Определить вид системы и решить её:
Учащиеся в группах анализируют системы, определяют их вид, затем, в ходе фронтальной работы обсуждают решения систем.
симметрическая, введем новые переменные x+y=u, xy=v
содержит однородное уравнение.
Пара чисел (0;0) не является решением системы.
IV. Контроль знаний учащихся
Самостоятельная работа по вариантам.
Решите систему уравнений:
Учащиеся сдают тетради учителю на проверку.
V. Домашнее задание
1. Выполняют все учащиеся.
Решите систему уравнений:
2.Выполняют «сильные» учащиеся.
Решите систему уравнений:
VI. Итог урока
Вопросы:
С какими видами систем уравнений вы познакомились на уроке?
Какой способ решения систем уравнений применяется при их решении?
Сообщение оценок, полученных учащимися в ходе урока.
Симметричные уравнения и их решение
Симметрическое уравнение нечетной степени имеет корень x = -1.
Симметрическое уравнение четной степени 2n с помощью подстановки $$ u = x + \frac<1>
Уравнения вида $$ a_0 x^ <2n + 1>+ a_1 x^ <2n>+ . + a_n x^
если $$\frac <
Возвратное уравнение нечетной степени имеет корень $$ x = — \lambda $$.
Возвратное уравнение четной степени 2n с помощью подстановки $$ u = x + \frac<\lambda >
Если обе части однородного уравнения разделить на $$ \left(
получим уравнение $$ a_0 t^n + a_1 t^
http://urok.1sept.ru/articles/512536
http://uztest.ru/abstracts/?idabstract=942393